基于可靠性评估的无人机零部件维修决策
2019-08-21谭壹方申翰林高丽霞
谭壹方 申翰林 高丽霞
中国民用航空飞行学院,广汉 618307
随着无人机技术的发展,目前对于无人机零部件及其子系统可靠性的研究一直是一个重要的研究方向。针对无人机系统故障,对其进行故障模式及特征分析,研究无人机维修问题对提高无人机的可靠性十分必要[1-3]。
现已有基于证据理论[4]、多层Bayes方法[5]及模糊数学理论[6]等方法运用至可靠性评估中。智能算法如支持向量机、人工神经网络等[7-8]在可靠性研究中多有报道,但输入样本大、计算收敛慢等问题导致在应用过程中难以实现。与此同时,一些学者针对无人机系统的维修做了相关研究[9-13],但多数为框架性基础研究,要实现在现场的操作和应用还有一定难度。基于此,本文针对无人机零部件提出一种基于可靠性评估的维修决策方法。该方法建立了无人机零部件的退化过程,将故障样本作为输入以获取过程参数,从而求解所评估的无人机零部件可靠性指标,依据此运用阈值分析方法对维修时间策略进行制定。以实际现场使用的无人机零部件故障样本为例进行了仿真,结果表明所提方法能够评估其可靠性,制定合理的维修时间决策,以保障其正常服役使用。
1 无人机零部件可靠性评估模型
1.1 零部件退化过程模型
在一般情况下,无人机各零部件自装配成型之日起其性能便开始不断衰退,零部件在服役使用期间也在不断老化、磨损和疲劳。随着使用时间增加,衰退的严重程度不断上升,如在零部件性能衰退期间发现,可进行人为修复或更换,否则不断的衰退将演变发展成为零部件故障,最终导致无人机整体的故障失效。由于无人机受天气、环境、突发事件等外界因素的影响很多,想要监控各零部件性能退化的中间过程十分困难。基于此,本文考虑以最终的故障状态记录为样本作为可靠性评估的输入,将外界因素作为加速零部件退化过程的条件,无论故障发生在何时,均认为其经历了逐步退化的过程,只是退化发展的速度不同,但导致的结果一致,都是故障失效需要人为修复或更换。因此,本文参照电气类元器件状态划分方法,将无人机零部件状态划分为正常状态、注意状态、异常状态和故障状态4类,建立无人机关键零部件的四状态Markov退化模型,如图1所示。
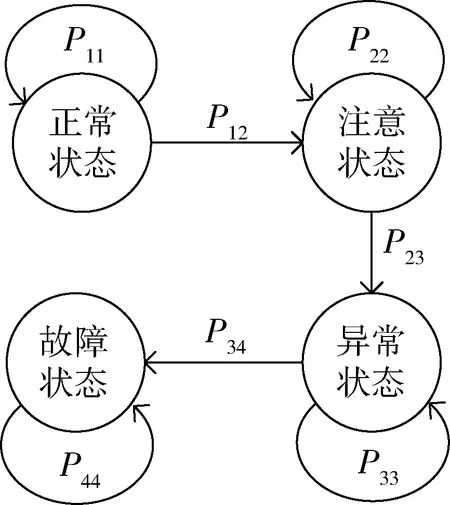
图1 无人机零部件Markov退化模型
因为无人机零部件的状态转移不易观测,同时以现有的维护记录手段做到完全准确的状态捕捉还难以实现,因此,该模型针对有关无人机零部件性能衰退或发生故障的样本信息说明如下[14]:①无人机零部件在目前状态条件下,其未来状态的演变规律独立于过去演变的过程,具有马尔可夫性;②起始时刻均认为零部件性能处于正常状态,记录时刻均处于最后的故障状态。故障状态结果体现了该零部件在记录时刻前所受各类因素影响累积的效果。
根据以上的说明,通过Markov退化过程的数学模型即可进行相应的过程参数求解,从而为可靠性评估工作获取关键参数。
1.2 Markov过程参数求解
由大数定律及Markov状态转移过程[14]推理可知,针对数量和故障统计样本量较大的无人机零部件而言,每种状态的停留时间可通过等分故障统计次数获得。设共计有总数量为M的某类无人机零部件,统计开始时刻设为ts,结束时刻为te。在ts~te统计时段内该类零部件共发生了Mf次故障,则通过将统计故障样本次数Mf等分来确定每种状态的停留时间。由于无人机零部件退化过程具有马尔可夫性,其状态停留时间服从指数分布,因此可得到该Markov过程参数如下[15]:
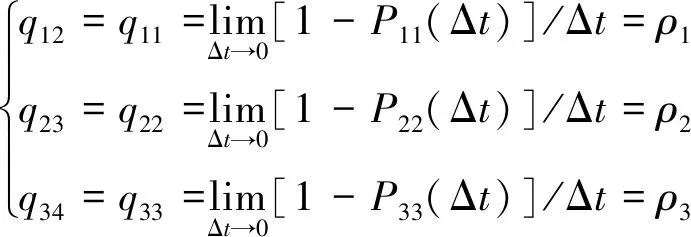
(1)
式中,q12,q23和q34分别为“正常”与“注意”、“注意”与“异常”、“异常”与“故障”状态间的状态转移速率;q11,q22和q33分别为“正常”、“注意”、“异常”状态维持速率,即维持在该状态、不发生转移的速率;P11(Δt),P22(Δt)和P33(Δt)则分别表示“正常”、“注意”和“异常”状态维持概率;ρi为第i种状态的停留时间Δti服从的指数分布参数。
1.3 可靠性参数求解
利用上述建立的Markov退化模型以及求取得到的退化过程参数,将各个状态的无人机零部件数量表示为对应的Markov状态集合[15-16]。
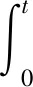
(2)
式中:M为该类无人机零部件的总数量;Bi(i=1, 2, 3)表示至t时刻为止由状态i转移至状态i+1的零部件数量值。
在上述状态集合中引入相关参数θ对该Markov状态集合进行推导,θ用来替换M代表零部件总数量,Markov状态集更新为:
(3)
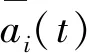
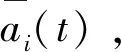
在t∈[0,T]定义零部件数量Ai,θ(t)的另一极限Ki(t)及其极限簇K(t)分别如下:
K(t)=(K1(t),K2(t),K3(t),K4(t))′
(6)
当t∈[0,T],T>0时,极限簇K(t)是一个期望为四行单列零向量的多元正态分布。
据此,分别令2个四行四列的矩阵为U(t)和V(t)。其中,矩阵U(t)表示如下:
ui,i(t)=-ρi, 1≤i≤3
(7)
ui,i-1(t)=ρi-1, 2≤i≤4
(8)
矩阵V(t)表示如下所示:
(9)
(10)
随之建立如下随机微分方程组:
dK(t)=Ι(t)K(t)dt+J(t)dB(t)
(11)
(12)
其中,K(0)=0;B(t)则是标准布朗运动的表达式[14-16]。常微分方程组,即式(12)的解为K(t)的协方差矩阵Σ(t),通过该协方差矩阵便能够求取得到极限Ki(t)的方差值。
那么,再结合式(4),得到Ai,θ(t)的近似值如下:
(13)
由近似关系可知,对于M个同类型无人机零部件,处于每一种状态的零部件数量均值和方差的近似值即为:
(14)
Var[Ai(t)]≈MVar[Ki(t)]
(15)
由式(14)和(15),可以获取所需评估的无人机零部件可靠性指标,从而求解处于各状态下的无人机零部件数量。同时,可以结合正态分布的特点,观察其期望和方差的变化情况。
2 基于可靠性评估的维修决策
在已知同类型无人机零部件总数量为M的条件下,设置各状态零部件数量阈值Li或零部件数量占比Ci,当满足式(16)或式(17)时
mi≥Li
(16)
mi≥Ci·M
(17)
输出对应的时间即作为相应的维修维护时刻信息。式中,mi为每种状态下的无人机零部件数量,即在得到同类型无人机零部件的评估结果后,运用阈值法获取对应的维修维护时刻ti。
综合上述有关无人机零部件可靠性建模,以及阈值比较,获得维修决策方法的整体过程如图2所示。
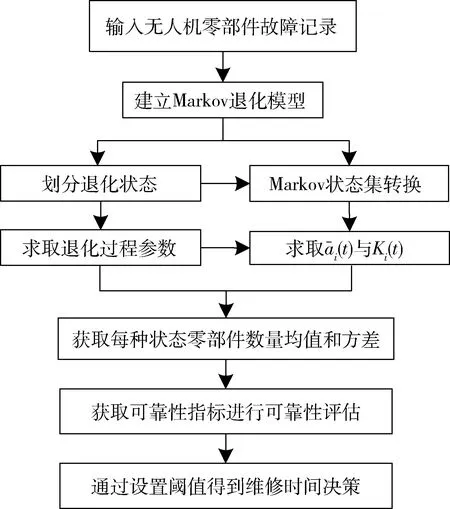
图2 基于可靠性评估的无人机零部件维修决策过程示意图
总体的方法流程为:首先,将同类型无人机零部件的故障记录数据作为可靠性评估的输入数据,通过数据处理获得故障次数及其统计时段区间,进而得到Markov退化过程参数。同时,通过Markov状态集合的转换求取极限值,以获取处于各个状态下零部件数量的期望和方差,输出可靠性指标,最后根据现场实际需求设置阈值,得到相应的维修时间信息,从而实现基于可靠性评估的无人机零部件维修决策。
3 算例分析
3.1 数据说明
对某无人机公司的60架同型号固定翼无人机的驱动电机故障样本数据进行分析。自2015年1月开始到2018年6月结束,统计时长共计30个月。根据记录显示,在此期间该类无人机的驱动电机一共发生了36次故障。按照等分故障次数所经历的时间间隔划分该零部件状态的停留时间区间,得到其退化过程参数q12,q23和q34分别为0.00255、0.00345和0.00510。
3.2 无人机零部件可靠性评估
利用所建立的Markov退化模型以及相应的公式,求解可得所评估时刻处于各个状态的无人机零部件数量的期望、方差与标准差。依据第2节的理论推导,能够得到处于各个状态的无人机零部件数量分布情况。下面选取自统计起始分别为6个月和18个月的正常状态零部件情况,以及自统计起始分别为12个月和24个月的故障状态零部件情况进行具体评估说明。
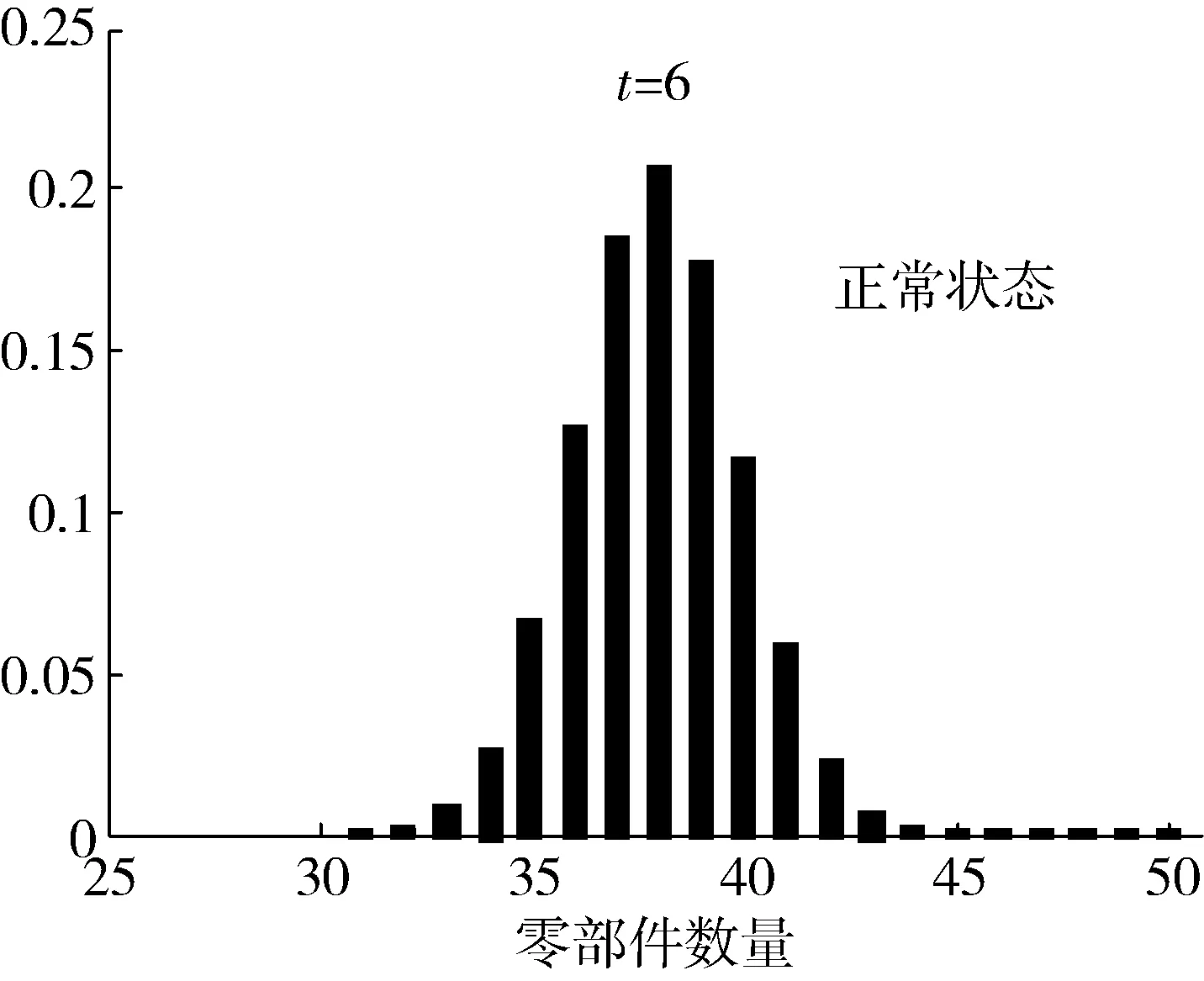
图3 统计开始6个月时处于正常状态的驱动电机数量结果
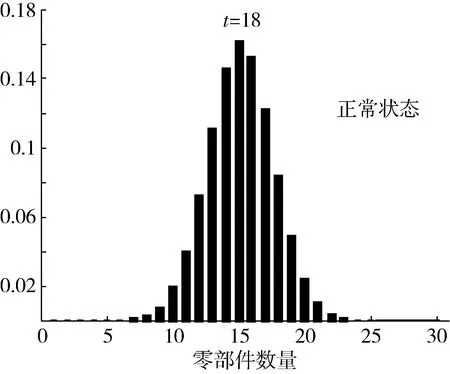
图4 统计开始18个月时处于正常状态的驱动电机数量结果
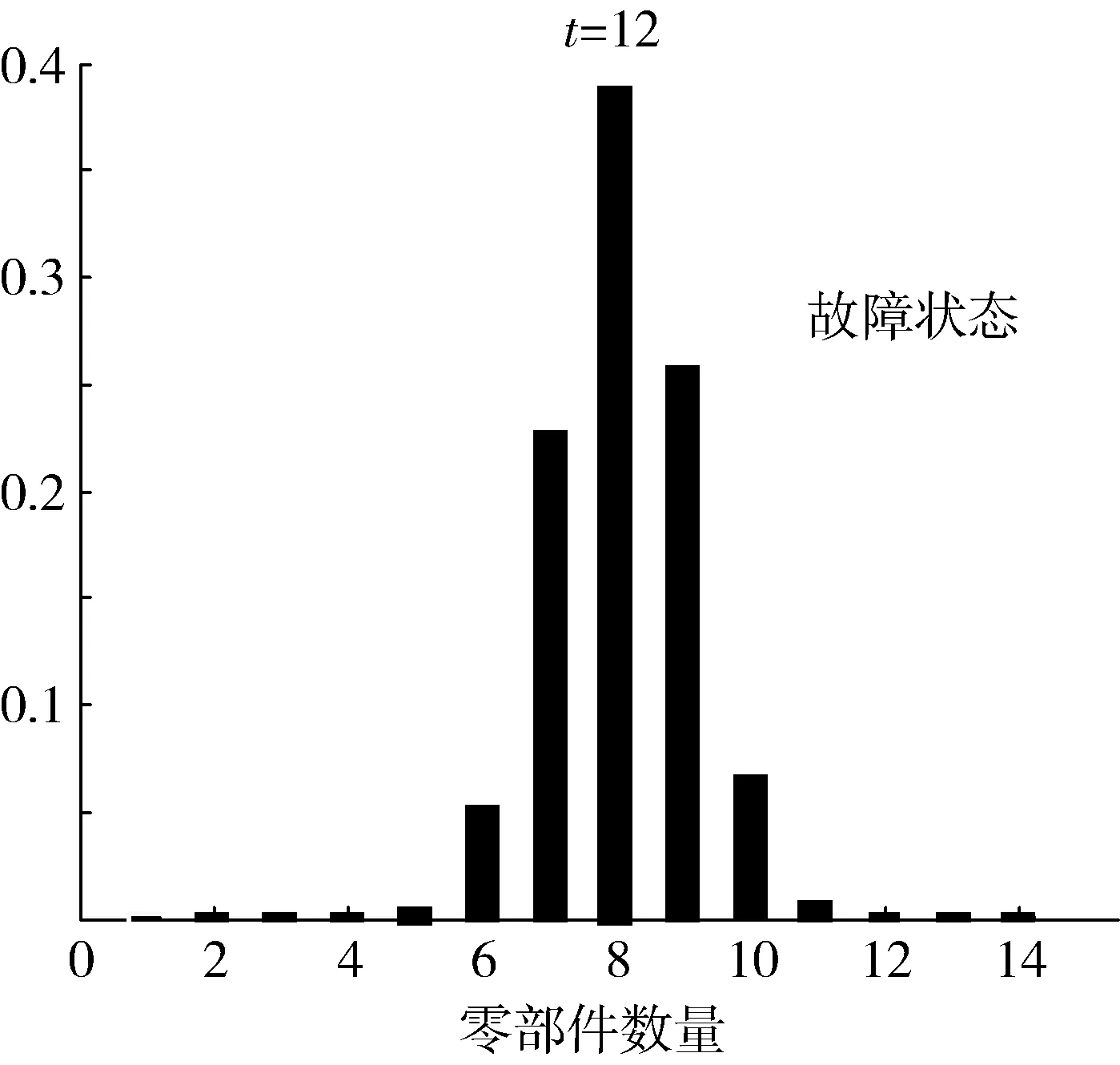
图5 统计开始12个月时处于故障状态的驱动电机数量结果
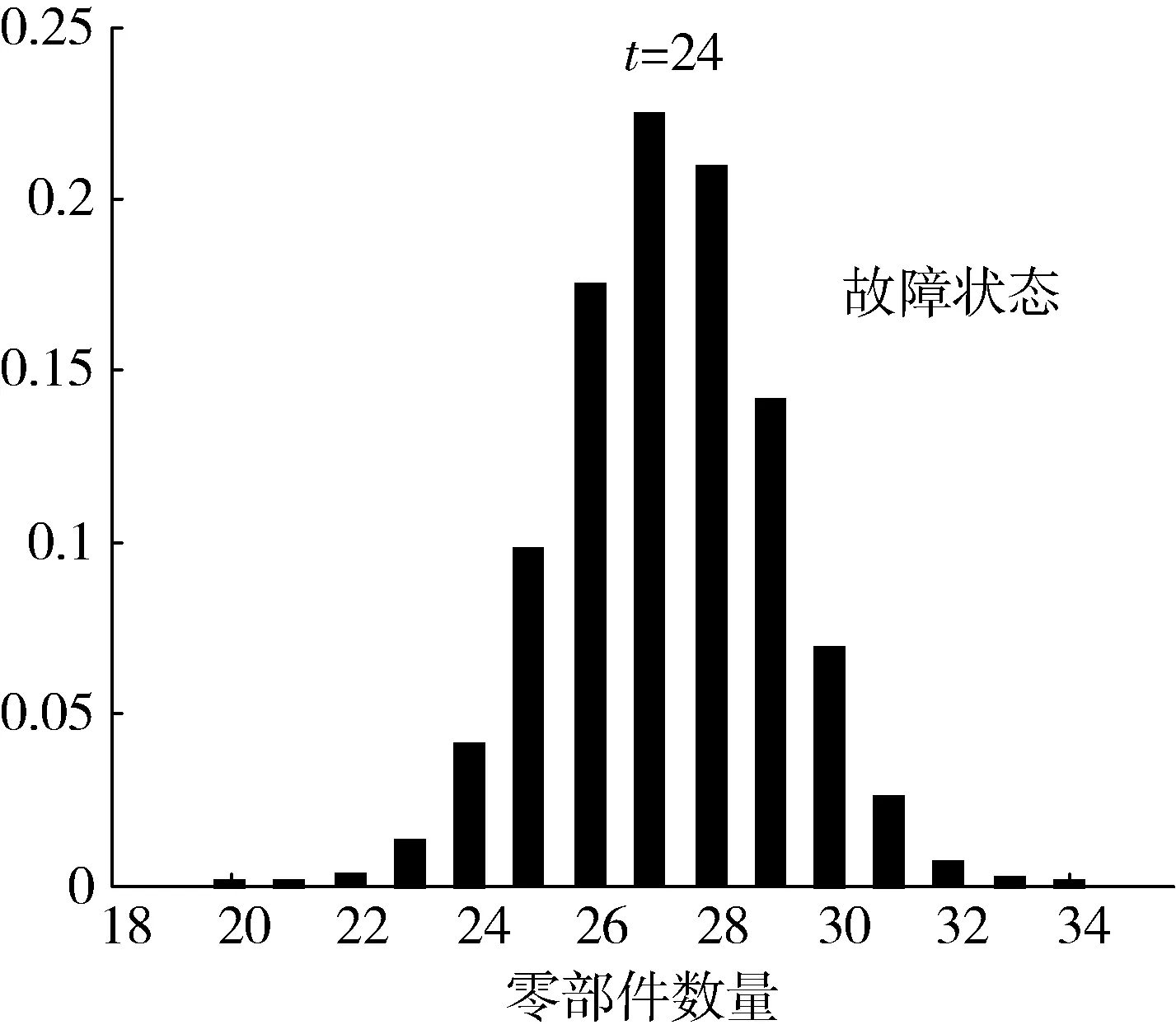
图6 统计开始24个月时处于故障状态的驱动电机数量结果
通过图3~6可以得出,在所选取的4个可靠性评估时刻,通过本文方法能够计算得到该类无人机驱动电机的正常运行台数及故障台数。在统计起始后的第6个月时,处于状态1的台数约为38台;在统计起始后的第18个月时,处于状态1的台数下降至15台左右。而在统计起始后的第12个月时,处于状态4的台数约为8台;而到了统计起始后的第24个月时,处于状态4的台数升至27台左右。这一评估结果与实际数据基本吻合,说明该方法能够较为准确地实现较大批量、同一型号的无人机零部件可靠性评估。
3.3 基于可靠性评估的无人机零部件维修决策
在维修决策所关心的周期性问题中,经过上述对无人机零部件的可靠性评估过程,连续计算求解得到自起始时刻60个月期间的马尔可夫状态集,获得其可靠性参数值,各个状态的驱动电机数量期望和方差结果如图8所示。

图7 统计期间各状态驱动电机数量期望结果
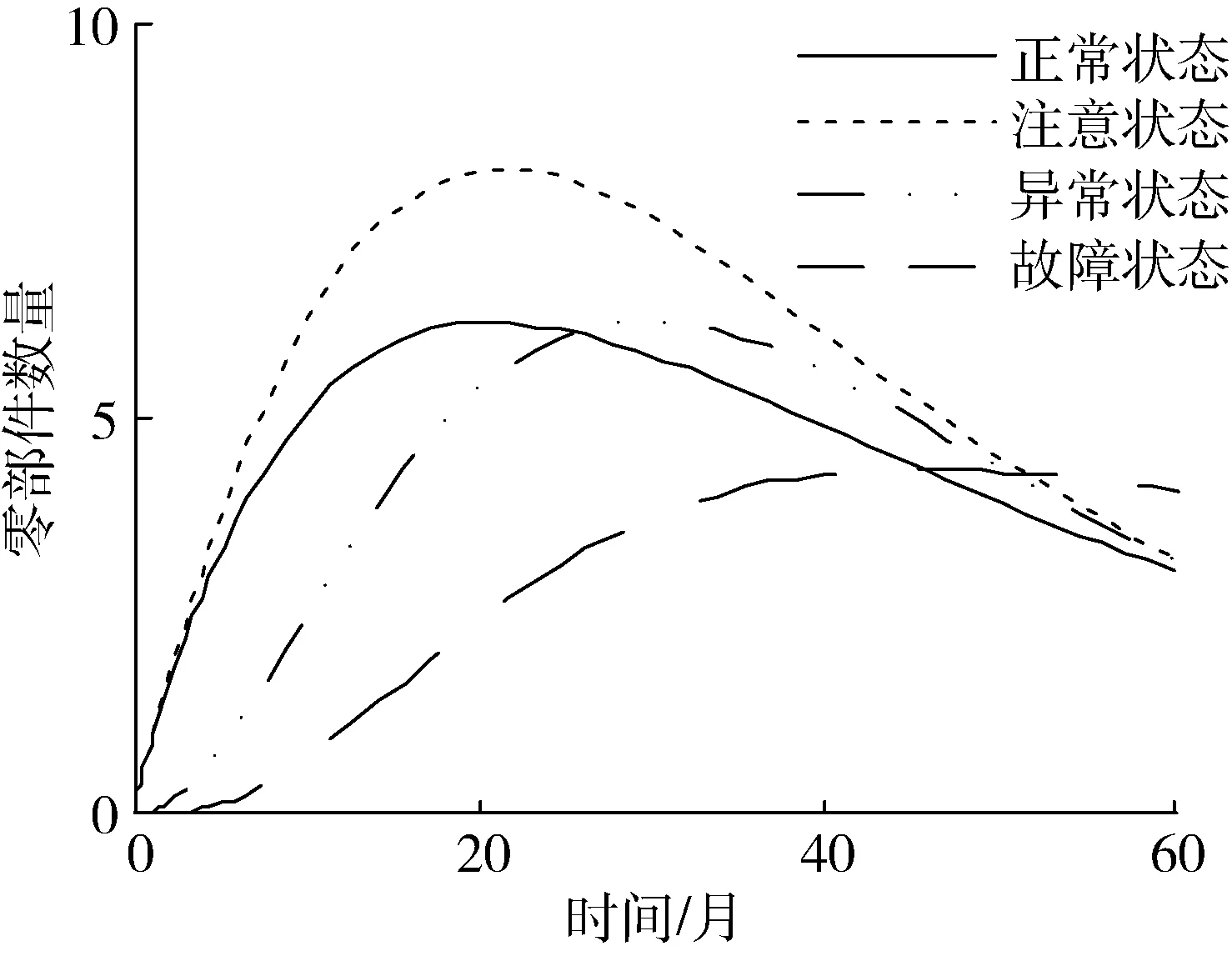
图8 统计期间各个状态驱动电机数量方差结果
由图7和8得知,随着服役时间的推移,处于正常运行状态的驱动电机数量不断减少,发展到故障状态的数量不断增加。而注意状态和异常状态均属于过渡状态,存在先增后减的趋势。因此,根据可靠性评估所得到的60个月期间各个状态零部件数量的期望结果,结合式(16)和(17)利用阈值法,设该批次无人机驱动电机注意状态和异常状态的数量占比Ci分别为
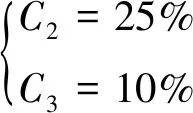
(18)
由此可以得到相应状态下的驱动电机数量阈值Li为
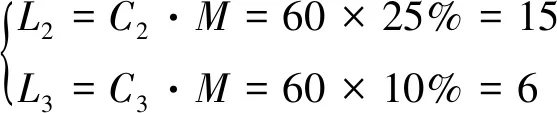
(19)
如图9所示,当处于注意状态和异常状态的零部件数量期望值达到分别设置的阈值L2和L3时,所对应的时间分别为5个月和8个月。
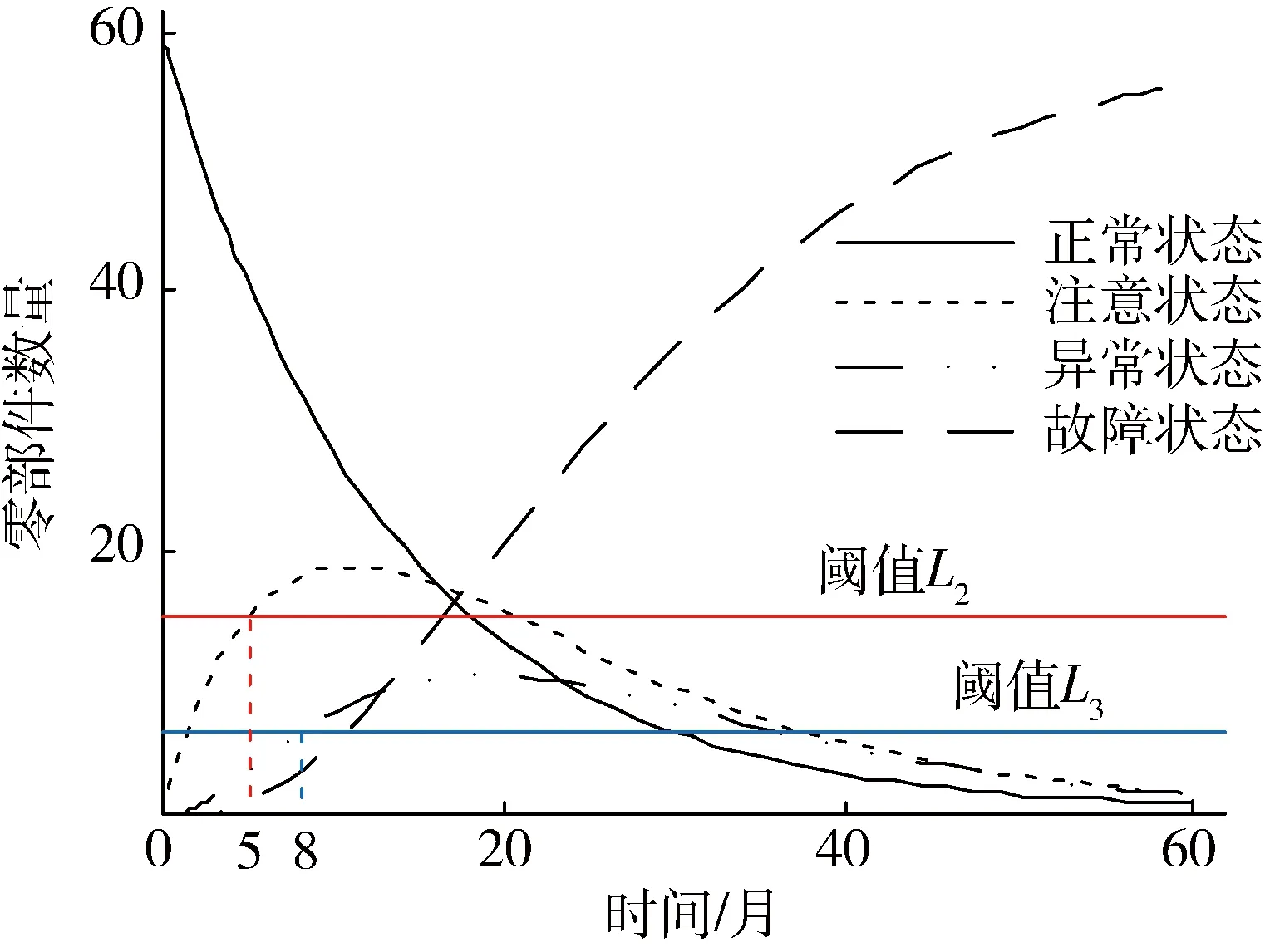
图9 注意状态与异常状态阈值曲线
通过阈值分析结果表明,该批量无人机驱动电机从投入使用开始后的第5个月,处于注意状态的驱动电机数量估计为15台,已达到所设阈值,应该对其进行检查维护和保养;而当使用至8个月时,处于异常状态的驱动电机数量将超过所设阈值,已达到了6台,且随之继续演变将导致处于故障状态的驱动电机台数增多,从而影响该批量无人机的正常服役和使用,因此应在投入使用第8个月时对该批量无人机驱动电机采取相应检查维修措施。
4 结论
提出一种基于可靠性评估的无人机零部件维修决策方法。该方法首先建立了无人机零部件的可靠性评估模型,利用Markov退化过程并将零部件故障样本作为输入数据,得到过程参数以求解可靠性指标,最后根据评估结果结合阈值分析得到维修时间决策结果。以实际投入使用的固定翼无人机驱动电机故障数据作了仿真分析,结果表明该方法能够较为准确地评估无人机零部件可靠性状况,结合所设阈值得到相应的维修时间,可为无人机使用者和维修人员更好地掌握无人机及其零部件可靠性状态发展趋势,提供相应的维修决策信息。
