夹芯结构的疲劳裂纹损伤扩展研究

罗白璐，朱英富，李之达，郑绍文

（1.中国舰船设计研究中心，武汉430064；2.武汉理工大学，武汉430063）

0 引 言

复合材料疲劳损伤演化规律及作用机理的研究，对于材料的疲劳力学研究有着很重要的意义。Mao[1]依照材料的疲劳损伤演化会经历三个阶段，基于唯象角度标示出了循环次数和复合材料整体损伤之间的关系。Montesano[2]指出在疲劳损伤的过程中应该注重有可能会发生的局部应力重分配情况，导致疲劳累积损伤演化。Singh[3]基于能量角度，选用双参数威布尔分布，将所研究的复合材料的临界能量释放率进行了定义，并对可能发生的数值波动进行统计，通过建立损伤演化模型探讨了在双轴疲劳载荷情况下碳纤维和玻璃纤维的损伤演化过程和应力-应变等关系。

本文应用累积损伤力学理论，以夹芯复合材料板为研究对象，开展了复合材料在交变载荷下疲劳累积过程的演化规律研究，借助于能敏感反映复合材料性能的刚度量，建立了夹芯复合材料结构在弯曲交变载荷作用下的结构疲劳累积损伤渐降模型。对全寿期内裂纹的萌生及扩展的全历程规律进行了描述，并采用刚度衰减作为复合材料结构失效状态控制量，最终构建了一个含疲劳全过程分析的宏观唯象损伤模型。

1 累积损伤分析

在应变以及应力的作用下，在某一点或者是某些点的地方会出现一些永久性的变化，而这些变化会随着循环次数的增多发生进一步的扩大，最终导致材料发生累计损伤。在材料的前期其内部会出现大量的裂纹，当裂纹的数量达到一定的程度以后就会有断裂的情况发生。然而，当材料到了其寿命后期的时候，此时因为材料累积了大量的来自于各方面的损伤，促使裂纹发生快速的扩散，在宏观上表现出材料突然的断裂。如图1所示。

图1 复合材料疲劳损伤演化规律Fig.1 Evolution rule of fatigue damage of composite materials

若将l1表示为损伤标量的弹性模量减少

因此复合材料结构的损伤变量D可做如下定义：

式中：D（n）表示加载n次后的结构损伤量；E（0）表示复合材料的初始弹性模量；E（n）表示加载n次后材料的剩余弹性模量。

如果材料发生疲劳断裂时，即复合材料的刚度为E（）

N时：

2 损伤过程中材料性能退化

受疲劳加载的影响，随着加载循环次数的逐渐增加，局部区域的材料性能会出现突降，外在的主要表现体现为材料刚度的下降，而这与该区域结构的应力状态无关。因此，我们在材料的衰变过程中，采用剩余刚度的方法来考核和预测复合材料的疲劳寿命。本文定义循环n次下材料的切线刚度为E（n），称之为剩余刚度，以便描述材料的疲劳损伤程度。

根据Yang[4]等人所提出的剩余刚度退化公式

式中：n表示载荷加载的循环次数；E（）0代表其初始刚度。

在疲劳循环作用下，由于复合材料的循环次数和刚度呈反比例关系，因此上式中Qv＞0。

将（4）式从n1到n2进行积分，可得

当n1=0，n2=n时，可以将（5）式转化成为：

当n=N时，N表示材料的疲劳寿命，（6）式进一步转化为：

因此，变量Q表示为：

而在（8）式中代入（6）式可得下式：

结合Lee[5]提出的剩余刚度与强度的关系表达式

式中：σU为结构的静极限强度；σ为所施加的疲劳应力值；c1及c2为试验模型常数，且c1≥1，c2＞0。

（10）式可转化为

将其代入到上述剩余刚度退化模型（9）式中得

式中：V代表与疲劳载荷应力相关的线性函数，可表示为V=a+bσ，a及b为试验系数。

因此，剩余刚度模型可进一步转化为

3 试验研究

3.1 试验对象

取常幅载荷疲劳试验在5个应力水平下进行，每个应力水平下取3个试件为实验对象来考察夹芯复合材料结构在常幅载荷下的弯曲疲劳行为。试件外观尺寸如图2所示。

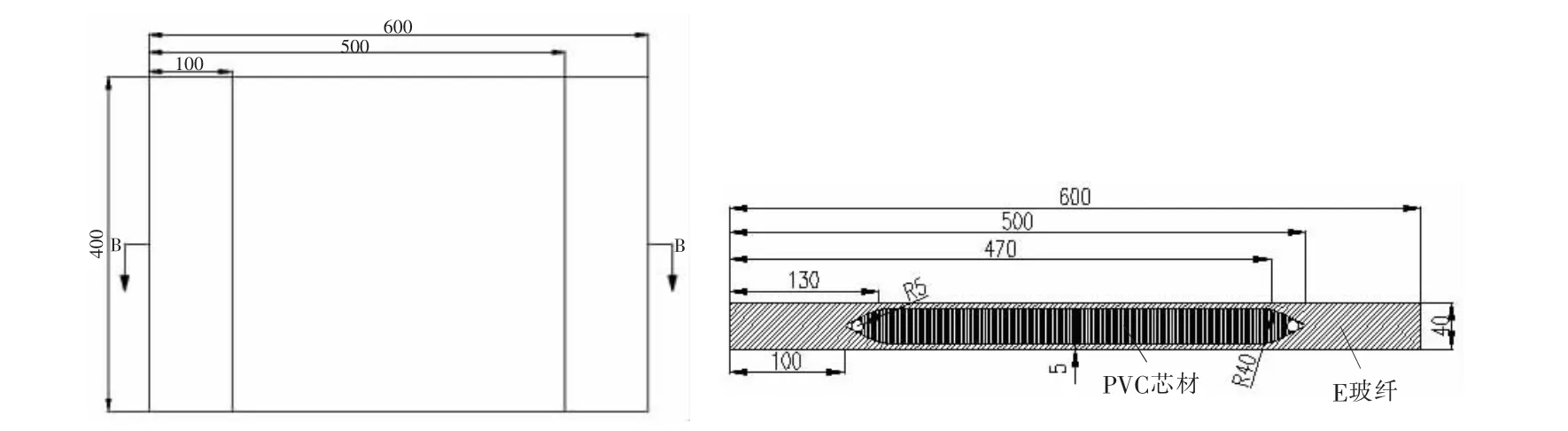
图2 试件尺寸Fig.2 Specimen size

3.2 试验方法及条件

考虑到除了遭遇主机振动的局部高频载荷影响的构件外，承受舰船正常使用中的波浪交变载荷谱的船舶结构，经常使用的是104～106次循环范围内的疲劳寿命曲线。因此，本文将到达106次循环而未发生破坏作为整个结构失效的条件疲劳极限。

图3 三点弯曲疲劳加载图Fig.3 Diagram of three-point bending loading

表1 疲劳试件编号Tab.1 Serial number of fatigue specimen

3.3 试验结果

图4 疲劳荷载取45%Pmax时试件损伤图（a1，a2为疲劳裂纹）Fig.4 Damage state at 45%Pmax fatigue loads(a1,a2 represent fatigue cracks)

图5 疲劳荷载取45%Pmax时试件裂纹扩展图Fig.5 Crack propagation curve at 45%Pmax fatigue loads

这些试件的疲劳损伤图均反映出，在疲劳载荷作用下，夹芯复合材料板的初始破坏区域均为中间芯材层的泡沫内。随着循环次数增加，多条贯穿泡沫芯材的裂纹会沿着纤维与芯材的界面层继续扩展，直至泡沫与纤维层完全分离。当芯材层的裂纹扩展至纤维界面的裂纹扩展时，当泡沫与纤维层完全脱离，此时试件的整体刚度急剧下降，试件也很快发生破坏。

图6 疲劳荷载取45%Pmax时试件刚度曲线Fig.6 Stiffness curve at 45%Pmax fatigue loads

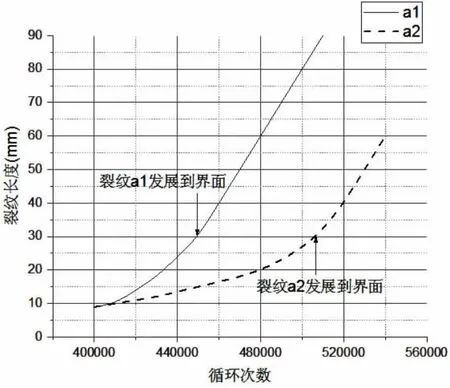
图8 疲劳荷载取50%Pmax时试件裂纹扩展图Fig.8 Crack propagation curve at 50%Pmax fatigue loads

图9 疲劳荷载取50%Pmax时试件刚度曲线Fig.9 Stiffness curve at 50%Pmax fatigue loads

图10 疲劳荷载取55%Pmax时试件损伤图Fig.10 Damage state at 55%Pmax fatigue loads(‘a’represents fatigue crack)

图11 疲劳荷载取55%Pmax时试件裂纹扩展图Fig.11 Crack propagation curve at 55%Pmax fatigue loads

我们可以将试件在泡沫芯子内的裂纹萌生扩展定义为第一阶段微裂纹扩展，而裂纹在纤维与芯子界面的扩展定义为第二阶段断裂裂纹扩展。无论在何种疲劳应力水平下，第一阶段的裂纹扩展都占了试件全寿命的绝大部分时间，第二阶段的扩展过程不仅迅速且无任何征兆的结束，直接破坏，整体过程呈现明显的脆性破坏特征。

图12 疲劳荷载取55%Pmax时试件刚度曲线Fig.12 Stiffness curve at 55%Pmax fatigue loads

图13 疲劳荷载取60%Pmax时试件损伤图Fig.13 Damage state at 60%Pmax fatigue loads(‘a’represents fatigue crack)

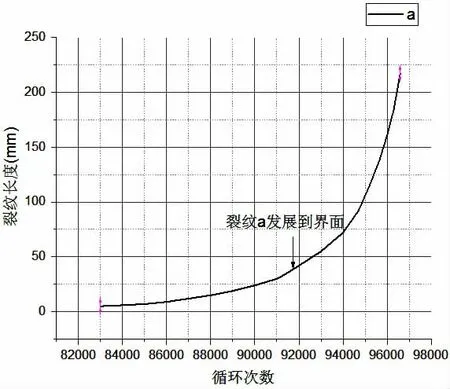
图14 疲劳荷载取60%Pmax时试件裂纹扩展图Fig.14 Crack propagation curve at 60%Pmax fatigue loads

图15 疲劳荷载取60%Pmax时试件刚度曲线Fig.15 Stiffness curve at 60%Pmax fatigue loads

在这两个显著的失效扩展阶段，由试件的刚度曲线图可以看出，在第一个微裂纹的萌生和扩展阶段，试件刚度缓慢下降；第二个断裂裂纹快速扩展阶段，试件刚度剧烈下降。刚度缓慢下降段可以被看成是损伤的增长段，这个阶段基本上占了试件寿命的90%。刚度的剧烈变化段可以看作是破坏的产生与发展阶段，试件的损伤发展到一定程度后，当出现大的贯通芯材的裂纹或是芯材滑移，直至无法满足试件承载力的要求时，试件最终完全失效破坏。

表2 60%Pmax应力水平下试件的剩余刚度（kN/mm）Tab.2 Residual stiffness at 60%Pmax fatigue load(kN/mm）

表3 55%Pmax应力水平下试件的剩余刚度（kN/mm）Tab.3 Residual stiffness at 55%Pmax fatigue load(kN/mm）

表4 50%Pmax应力水平下试件的剩余刚度（kN/mm）Tab.4 Residual stiffness at 50%Pmax fatigue load(kN/mm）

表5 45%Pmax应力水平下试件的剩余刚度（kN/mm）Tab.5 Residual stiffness at 45%Pmax fatigue load(kN/mm）

表6 40%Pmax应力水平下试件的剩余刚度（kN/mm）Tab.6 Residual stiffness at 40%Pmax fatigue load(kN/mm）

夹芯复合材料板在弯曲疲劳试验的循环加载过程中，各疲劳应力水平下的剩余刚度试验数据见表2-6。

结合表4，以50%Pmax疲劳载荷应力水平为对象，将试件的剩余刚度和初始刚度之比E（n）/E（0）为纵坐标，循环次数n与50%Pmax应力水平下的疲劳寿命N之比为横坐标，绘成如图16的夹芯复合材料板弯曲疲劳剩余刚度退化曲线。

从图16可以看出在未完全失效前，剩余刚度退化率非常缓慢，仅在临界失效段才出现快速“断崖式”的下降。根据以上退化趋势，结合剩余刚度退化模型，使用最小二乘法进行数值拟合，得到剩余刚度退化模型中的参数C1=1.018，C2=0.698，a=0.657，b=1.861，最终代入（13）式，得到夹芯复合材料板的弯曲剩余刚度退化模型：

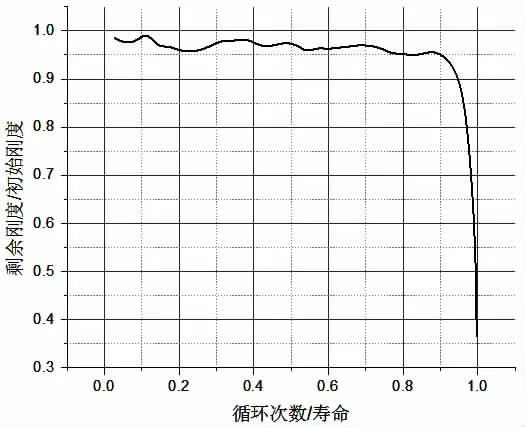
图16 夹芯复合材料板弯曲疲劳剩余刚度退化曲线Fig.16 Residual stiffness degradation curve of sandwich composite plates

表7 60%Pmax应力水平下剩余刚度模型计算值与实测值对比Tab.7 Comparison of residual stiffness values between calculation and measured fatigue load at 60%Pmax

续表7

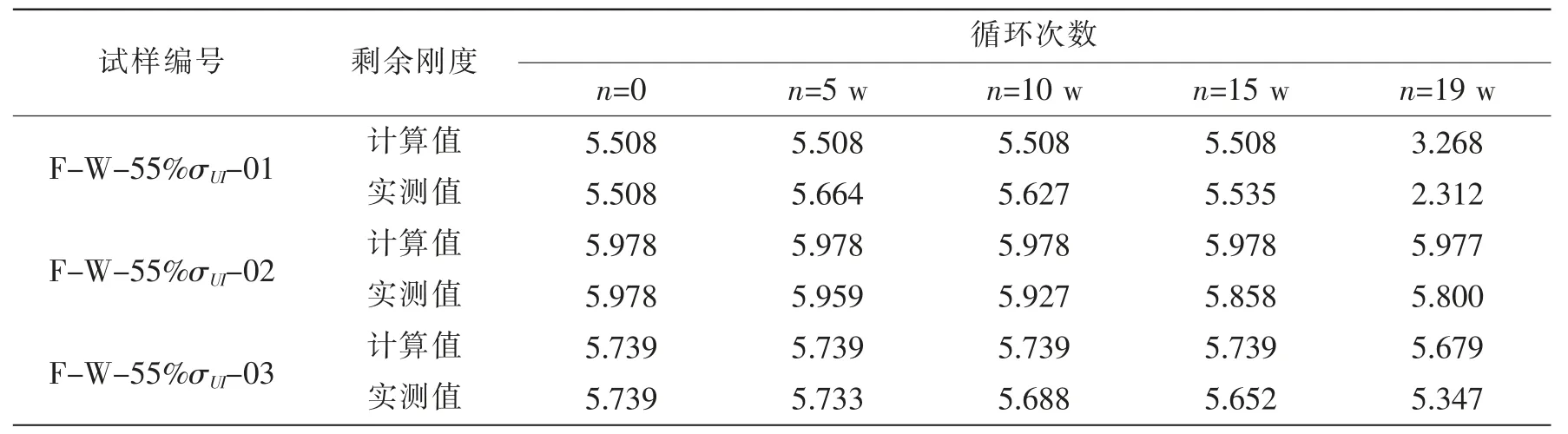
表8 55%Pmax应力水平下剩余刚度模型计算值与实测值对比Tab.8 Comparison of residual stiffness values between calculation and measured fatigue load at 55%Pmax

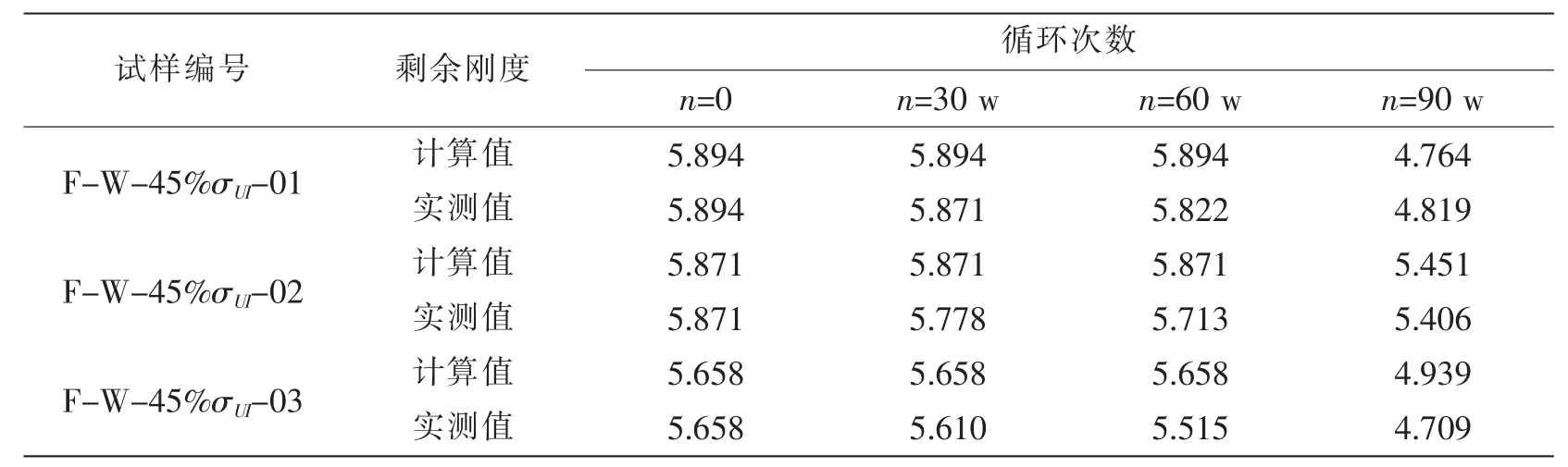
表9 45%Pmax应力水平下剩余刚度模型计算值与实测值对比Tab.9 Comparison of residual stiffness values between calculation and measured fatigue load at 45%Pmax

表10 40%Pmax应力水平下剩余刚度模型计算值与实测值对比Tab.10 Comparison of residual stiffness values between calculation and measured fatigue load at 40%Pmax

利用上式计算其他各应力水平下试件各阶段的剩余刚度值，对比各阶段的实测值见表7-10。

上述计算值与实测值对比分析可以看出，（14）式拟合的剩余刚度退化模型的适用性较好，在不同应力水平60%Pmax，50%Pmax，45%Pmax和40%Pmax下，阶段性的剩余刚度退化值预测的一致性均较好。

4 结 论

（1）在疲劳典型失效特征方面，试验结果表明，作为孔穴材料的芯材，在循环载荷作用下易被粉碎（压实），导致弯曲试件横截面上的中性层偏移。因此当加载卸载交替进行时，伴随着宏观刚度的下降，使得芯材开始沿第一主平面撕裂，并缓慢扩展。当这个漫长阶段结束，即芯材中裂纹扩展至蒙皮时，裂纹开始沿芯材与蒙皮间界面快速扩展，芯材与蒙皮层合板之间完全分离，试件刚度呈现“断崖式”下降，随之试件丧失承载力并最终破坏。

（2）夹芯复合材料结构在承受疲劳载荷作用时，材料内部会产生多种损伤形式，在宏观上的表现为材料力学性能的衰减，且衰减程度与加载次数间为非线性关系。本文在研究了复合材料疲劳损伤与其刚度衰减间的相互联系的基础上，提出损伤扩展速率统一的“缓→快”型变化趋势，并基于此建立了描述材料损伤演化的宏观唯象损伤模型，全面反映了复合材料全寿命阶段内的损伤演化历程。

（3）从裂纹的扩展延伸特征及与试件刚度的变化过程进行对比分析后可看出，不论施加的交变应力水平的大小如何，夹芯复合材料结构中的裂纹扩展均呈现明显的两个阶段。第一阶段，泡沫芯子内微裂纹萌生与缓慢扩展，试件刚度缓慢变化，整个历程约占试件全寿期90%的时间；第二阶段，芯子与纤维层界面层的裂纹快速贯穿扩展，试件刚度骤降式下降，整个历程约占试件全寿期10%的时间。