基于ABAQUS的地震荷载作用下高土石坝心墙动力响应特性分析
2019-08-21欧念芳
欧念芳,李 阳
(湖北省水利水电科学研究院,湖北 武汉 430070)
土石坝是由堆石、土体和其他一些材料组成的一种坝型,由于其可以就地取材、对地形要求不高、方便管理等优点在世界范围内被广泛应用[1]。近些年地震发生的频率越来越高,土石坝失事的后果非常严重,因此加强其在地震荷载作用下的动力稳定问题研究就显得尤为重要。
Hardin和Drnevich[2]采用双曲线模型对土石坝的动力特性进行研究,并提出了他们的一些优化建议。李万红等[3]人在前人的研究基础上提出了新的动力模型,用来进行土层在地震荷载作用下的动力响应。著名学者沈珠江[4]在土石坝本构模型上进行许多研究,并提出了新的优化公式。徐晶昌[5]对病险土石坝的施工技术进行了研究,但是他没有考虑地震荷载对坝体和心墙的影响。Duncan和Chang[6]提出了著名的Duncan- Chang双曲线模型,该模型到现在仍然被广泛应用。顾淦臣[7]、李湛[8]等人使用有限元软件进行了不同程度的地震荷载作用下的动力稳定研究。张波等[9]人采用动力非线性模型对土石坝的地震反应进行研究。
本文在前人对土石坝的研究基础上,以有限元软件ABAQUS为基础,对高土石坝在地震荷载作用下心墙的动力响应进行研究,为大坝预防地震提供参考。
1 研究方法
本文选取工程为某以发电为主兼顾防洪、灌溉等效益的高土石坝,该工程为1级建筑物。水库库容为64.28亿m3,最大坝高为186 m、上、下游的坝面坡度分别为1∶2.1和1∶1.9,坝顶长度为545 m。坝体内由不同的材料组成,主要有堆石、砾石等。大坝抗震标准为百年一遇。
以大型有限元软件ABAQUS为基础对蓄水期内该高土石坝心墙在地震荷载作用下的动力响应进行分析。本文动力响应计算采用等效线性模型,在模型中应力应变计算公式为:
τ=Gγ+ηγ/T
(1)
式中:τ为切应力,Pa;G为剪切模量,Pa;η为剪切粘滞系数,Pa·s;γ为切应变;T为时间,s。
剪切粘滞系数的计算公式为:
η=2Gλ/ω
(2)
式中:λ为阻尼比;ω为圆频率,s-1。
著名学者沈珠江[10]在等效线性模型基础上进一步提出的等价线弹性模型在目前的地震动力时程的分析中比较准确,并应用广泛,相关公式如下:
(3)
(4)
坝体不同部位采用不同给的材料,不同材料对应的模型参数见表1。本文采用的地震波为人造波,地震波时程曲线见图2,时程间隔时间为0.02 s,模拟中地震波持续时间为40 s。

表1 等效线性模型材料参数

图1 地震波时程曲线
在进行数值模型时根据坝体的材料分别定义,坝体整体使用结构化网格,共计网格数量为563 214个、节点数为573 621个。坝体分级实际情况划分成20级,共计采用4次分级施加的方式,具体施加过程见图2。
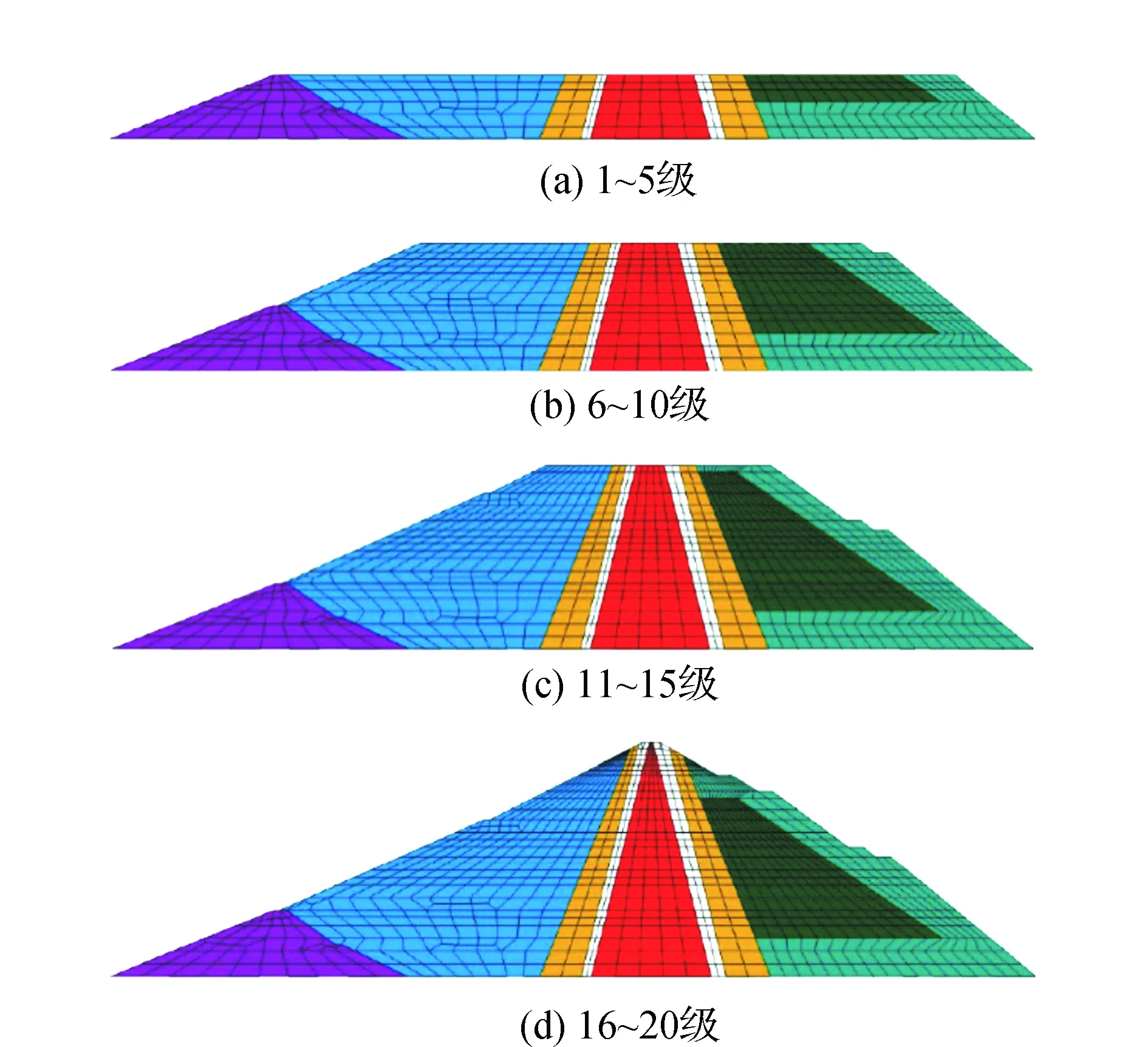
图2 坝体荷载分级施加图
2 结果分析
2.1 模态分析
等效线性模型涉及圆频率,将其设置为1进行相关的模态分析,计算得出坝体的第一阶振型如图3所示。
根据图3可知,坝体的圆频率为1.24 s-1。根据得到的坝体的圆频率,将对应的参数设置为1.24 s-1进行重新计算,并对坝体的切应变进行监测,得出心墙处最大剪应变沿坝高方向的分布情况,见图4。
从图4可以看出,在我们进行的5次迭代计算分析中,第一次切应变较大,第二次切应变明显减小,第三次已经趋于稳定和第四次、第五次区别很小,故认为在第三次已经收敛。根据图4 曲线变化趋势可知,沿着坝高切应力逐渐增加,然后迅速减小,最大值出现在坝高150 m附近处。
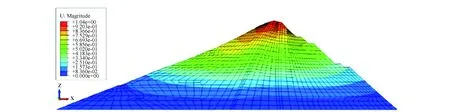
图3 坝体第一阶振型
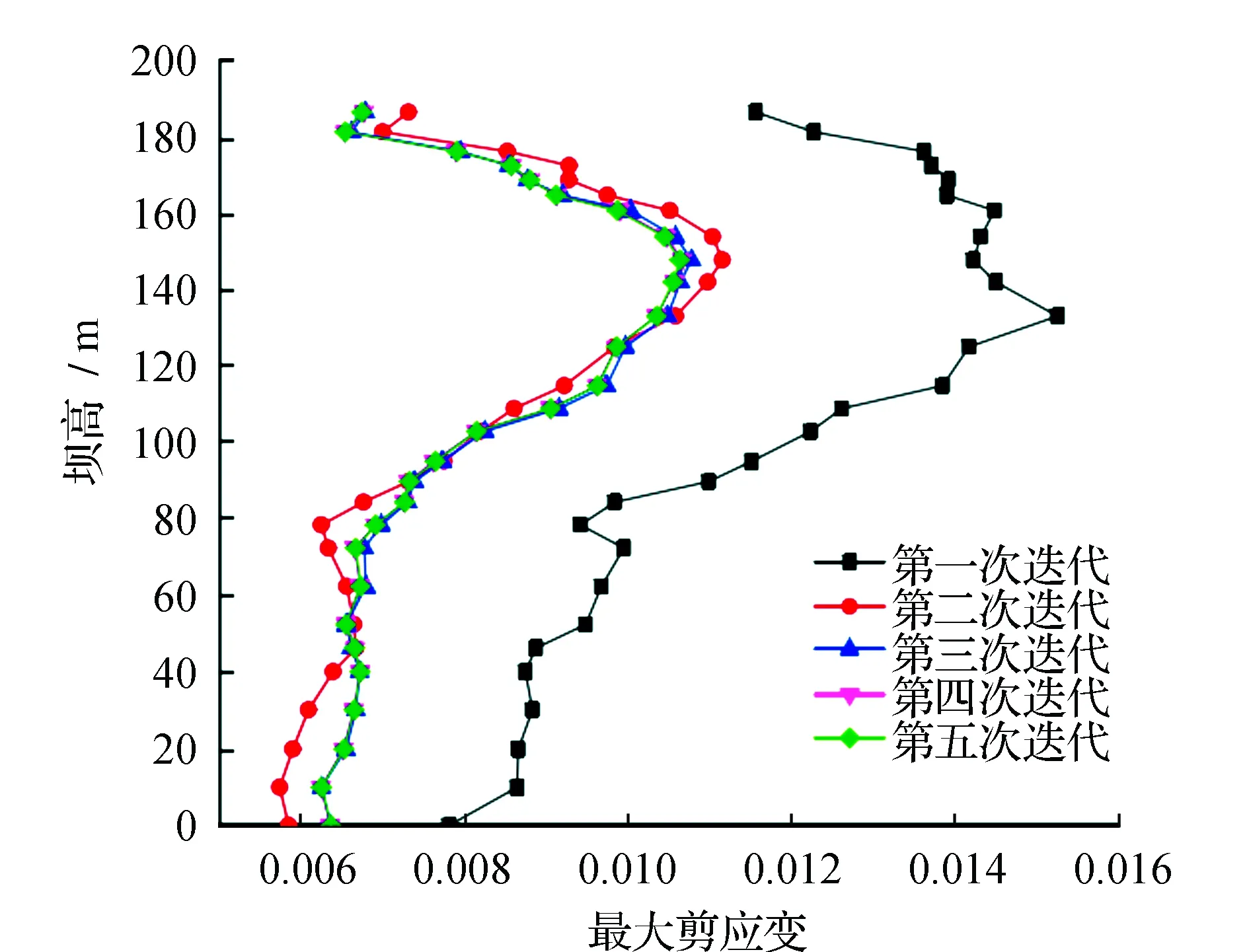
图4 心墙处最大剪应变沿坝高方向分布
2.2 应力分析
计算后心墙主应力分布云图见图5。根据图5可知,在地震过程中心墙的应力变化比较大,由图5(a)知在心墙的整体处于受拉状态,拉应力最大值出现在心墙底端,大小为2.86×105MPa。根据第三种应力分析,心墙在中间位置出现了明显应力集中现象,最大拉应力和最大压应力均出现在中间靠上位置附近,最大拉应力和最大压应力分别为:4.82×105MPa、9.51×105MPa。说明在地震过程中,心墙受力较大,需要进行适当的防护。
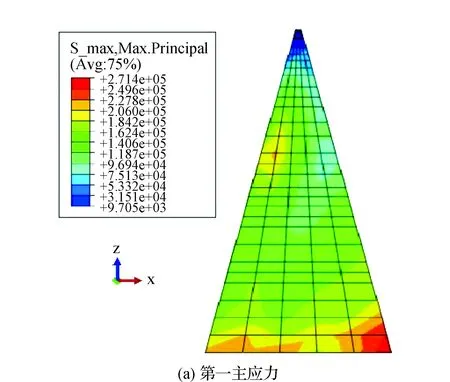
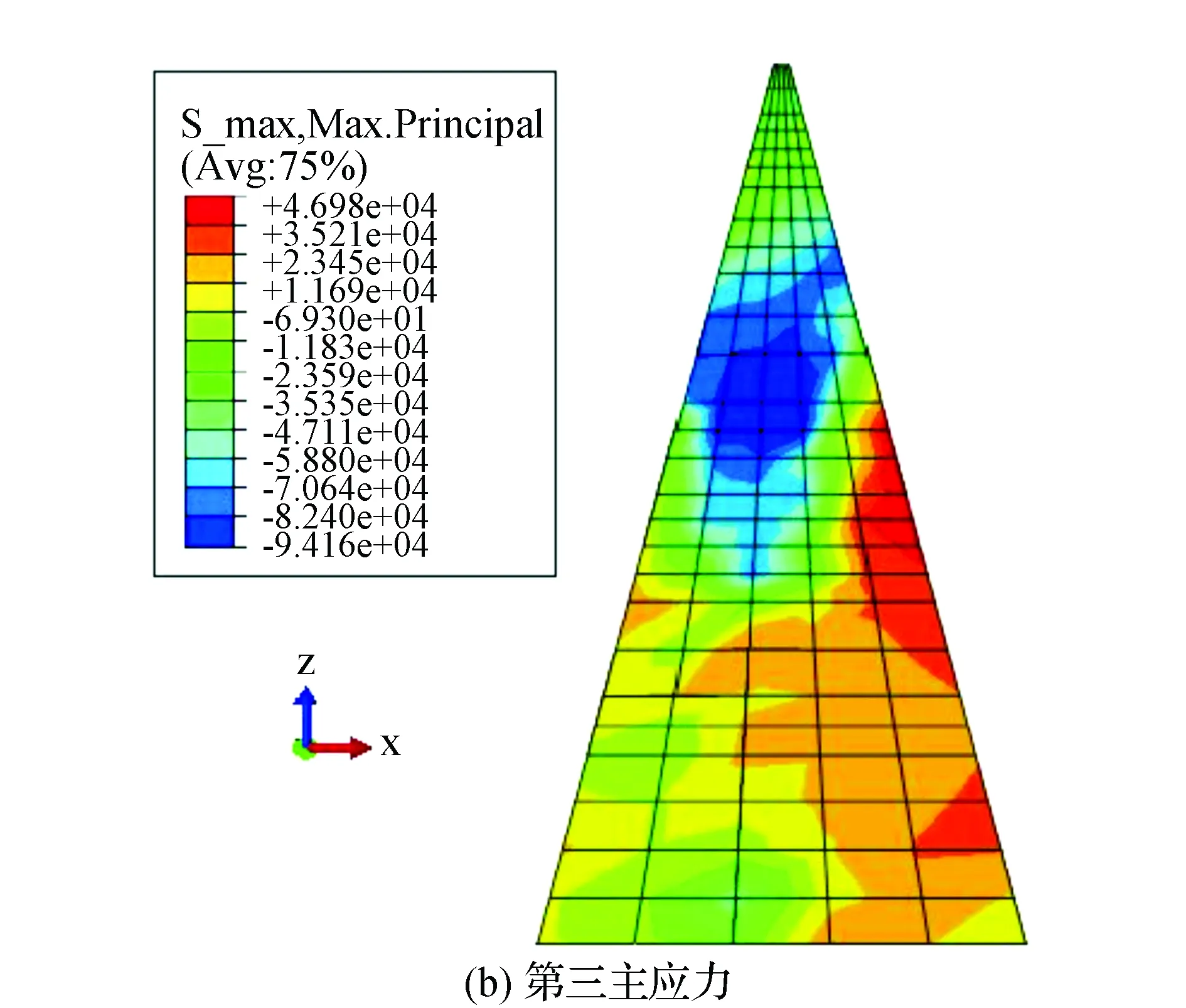
图5 心墙主应力云图
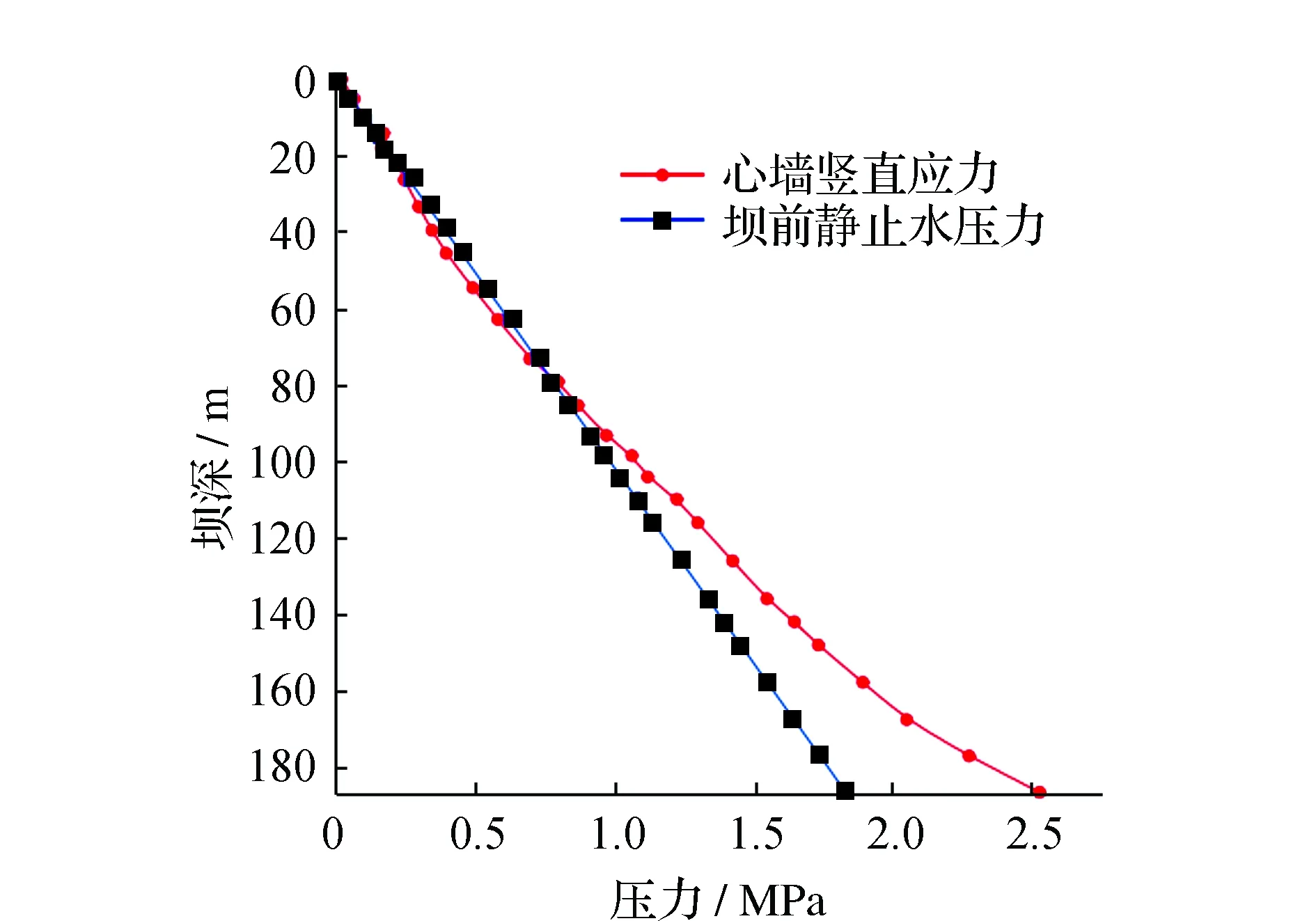
图6 心墙处竖向应力与水压力对比图
在地震过程中,心墙竖向应力变化也比较明显,对比进行分析见图6。根据图6可知,心墙的竖向应力沿着坝高由低到高逐渐减小,最大值出现在心墙底部,大小为1.82 MPa。竖向应力在较高高程时与坝前静水压力比较接近,随着水深的增加,静水压力增加的幅度较大,大于心墙竖直应力。
2.3 拱效应系数分析
计算后心墙的拱效应系数最小值沿坝高变化曲线见图7。

图7 心墙的拱效应系数最小值沿坝高变化曲线
根据图7可知,地震会引起心墙附近拱效应发生变化,心墙在地震过程中的拱效应最小值要小于蓄水期稳定运转的状态的下拱效应,最小值出现在沿坝高中间靠上位置,从坝顶向下大致60 m附近处,拱效应系数大小为0.27。在此位置处容易出现在水平裂缝。
对心墙上游底部拱效应系数在40 s内的时程变化进行分析,见图8。
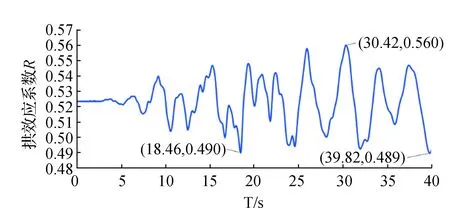
图8 心墙上游底部拱效应系数时程曲线
根据图8可知,在整个地震计算过程中,前2.80 s拱效应系数基本没有变化,然后受地震波的影响出现震荡式变化,最小拱效应系数分别出现在18.46 s和39.82 s,大小为0.490和0.489,两个时间均比地震波的波峰时间晚;最大值出现在30.42 s,大小为0.560。
2.4 加速度时程曲线分析
坝顶和坝底加速度时程曲线见图9。

图9 坝顶和坝底加速度时程曲线
根据图9可知,坝顶和坝底的加速度时程曲线明显不一样,坝顶的震荡幅度要大于坝底,并且震荡的时候要更久一些,坝底在接近35 s时已经趋于稳定,但是坝顶位置依然震荡明显。两个位置加速度最大出现的位置不同,坝顶和坝底出现最大加速度的时刻分别为:14.44 s、15.50 s,大小分别为:4.85 m/s2、-2.88 m/s2。
对心墙处最大加速度沿坝高的变化曲线进行分析,见图10。
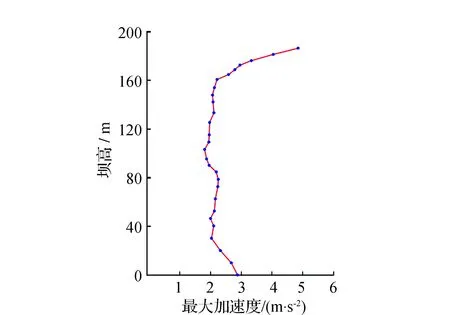
图10 心墙处最大加速度沿坝高变化曲线
根据图10可知,沿着坝高由底向上加速度先减小,然后在1.90~2.20 m/s2之间波动,达到某高度后再迅速增大。在坝底位置加速度大小为2.91 m/s2;加速度最小值出现在101 m附近处,大小为1.86 m/s2;坝顶加速度最大,大小为4.98 m/s2。
3 结 论
本文采用有限元软件ABAQUS对高土石坝在地震荷载作用下心墙的动力响应进行研究分析,得出以下结论:
(1)在坝体靠近上游大约2/3坝高位置处附近,心墙受力较大容易出现裂缝,要进行适当的加固和监测。
(2)在靠近坝顶60 m左右位置处,心墙的拱效应达到最小,大小为0.27。
(3)在地震过程中,坝顶加速度时程曲线震荡幅度明显大于坝底加速度震荡幅度。心墙在坝顶加速度达到最大值,大小为4.98 m/s2。
