自回归移动平均模型在北京市朝阳区手足口病发病预测中的应用

葛申 马建新 付凌姣 王晶 崔树峰 张政

手足口病是由多种肠道病毒引起的,以发热及手、足、口、臀等部位特征性皮疹或疱疹为主要症状的儿童常见传染病[1]。2008年，安徽省阜阳市曾出现较大规模流行[2]，同年5月，我国将其列入法定报告传染病管理。近几年，我国手足口病呈现发病强度高、高峰持续时间长、疫情分布广等特点[3]。北京市属于“热点”发病城市[4]，朝阳区手足口病发病数一直位于北京市发病数排名前列[5-6]。手足口病发病受到许多复杂因素的影响，一般回归预测很难获取并分析全部的相关因素。时间序列分析利用事物发展延续性规律，以时间为自变量，用历史监测值建立模型预测事物未来情况[7]。自回归移动平均模型(autoregressive integrated moving average model，ARIMA)是重要的时间序列分析预测模型，其操作方法方便、获取数据成本低、适用范围广、实用性强、短期预测精度较高，在传染病预测、预警方面有较多的应用。在预测手足口病方面，有研究表明ARIMA模型可以较好预测短期内的变化趋势[8]。因此，现通过ARIMA模型对朝阳区手足口病的发病进行时间序列分析并建立预测模型，以研究朝阳区手足口病流行特征和发展规律，为朝阳区手足口病的防控工作提供科学的参考依据。

1 资料与方法

1.1资料来源 中国疾病预防控制系统2010年1月1日-2016年12月31日现住朝阳区的手足口病监测数据。

1.2方法

1.2.1时间序列模型结构： 采用ARIMA模型，当观测值为平稳序列时，模型表达式为：

Yt=φ1Yt-1+φ2Yt-2+…+φpYt-p+

et-θ1et-1-θ2et-2-…-θqet-q

模型中Yt是时间序列在t期的观测值。当序列不平稳时，通过差分使其平稳，模型为ARIMA (p,d,q)。模型参数：p为自回归阶数，d为差分次数、q为移动平均阶数。若进一步考虑资料的季节性/周期性，则模型标记为ARIMA (p,d,q)(P,D,Q)s。新的参数P、Q为季节自回归和移动平均的阶数，D为季节性差分次数，s为季节性周期循环的长度，本文通过月发病数预测以12个月为季节性循环周期。

1.2.2模型建模步骤： 主要包括四个阶段：①序列的平稳化：ARIMA模型应用条件是预测对象的时间序列为平稳随机序列，不平稳的序列需要进行预处理，处理后通过进行分析确认;②序列特征识别和模型的识别：通过绘制并观察绘制时间序列图、自相关系数函数图(ACF图)和偏自相关系数函数图(PACF图)进行模型的初步识别，对模型进行定阶;③参数估计和模型诊断：利用非线性最小二乘法估计模型参数，采取从低阶到高阶逐步尝试的方法，依次拟合不同参数组合。确定参数后，对原始数据与拟合数据的残差序列进行白噪声检测，其检验方法为计算Box-Jenkins统计量(Q值);④模型预测应用：选定最佳模型后，对2016年朝阳区月发病数进行预测，将预测发病数与实际发病数进行比较，以验证模型效果。

1.3统计学方法 使用Excel 2013软件对收集到的数据进行汇总、整理，使用SPSS 21.0软件对资料进行统计分析和模型构建。

2 结果

2.12010-2015年朝阳区手足口病发病时间趋势 通过绘制2010-2015年手足口病月发病数时间序列图(图1)进行分析：朝阳区手足口病各月均有发病，呈明显季节性规律，5-7月出现明显的流行高峰，1-2月发病数最低，10-11月出现发病数反弹的情况，特别是2011年和2014年出现较为明显的小高峰，其他年份此特征不显著。从流行长期趋势来看，高发年份之后次年发病大幅下降，此后逐年小幅升高。

图1 2010-2015年朝阳区手足口病发病数时序分布

2.2模型构建 通过前述发病趋势分析发现，2010-2015年北京市朝阳区手足口病发病时间序列存在以12个月为1个周期的季节性特征，且序列波动较大，是不平稳的序列。对序列进行季节性差分和自然对数转换以平稳季节性波动和减少方差波动。平稳化后，通过观察ACF图(图2)和PACF图(图3)，ACF图呈震荡衰减形式，PACF图第一阶函数值特征显示，是典型的自回归过程，确定模型为季节乘积模型ARIMA(p,d,q)(P,D,Q)12。

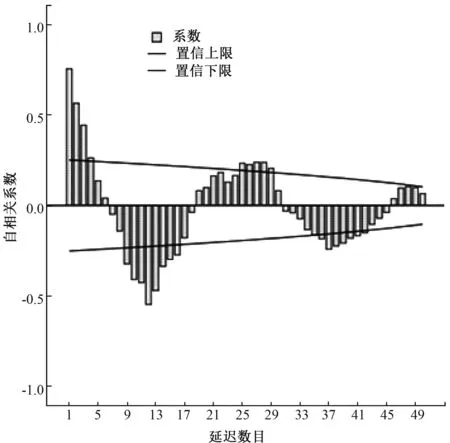
图2 原始时间序列经平稳化后自相关系数函数图(ACF图)

图3 原始时间序列经平稳化后偏自相关系数函数图(PACF图)

2.3参数估计和模型诊断 对模型的参数采取从低到高逐个进行尝试的办法，得出不同阶数组合的模型。经过筛选后选取标准化BIC值最小，R2较大且简洁的模型为最佳模型。模型ARIMA(1,0,0)(1,1,0)12的各参数值均有意义，R2=0.679表明模型拟合程度较好，标准化BIC值=10.894，在备选的模型中最小。采用Ljung-Box方法做残差白噪声检测，其Ljung-Box Q=22.59，P>0.05。做残差序列的ACF、PACF图(图4)，残差序列的自相关系数和偏自相关系数均落入95%CI中。证明残差序列为随机误差，提示模型已经将时间序列中蕴含的信息提取出来。

图4 模型ARIMA(1,0,0)(1,1,0)12残差序列ACF、PACF图

2.4模型预测应用 通过前述建模方法，对朝阳区2010年1月-2015年12月手足口病月发病数建模，对2016年1-12月的月发病数进行预测(图5)。以2016年1-12月的实际月发病数验证：预测结果与实际情况总体趋势一致，季节性规律基本相同，实际发病数在预测发病数的95%CI范围内波动，但预测发病数的平均相对误差达49.37%。将2016年1-6月的发病数序列继续纳入模型，对2016年7-12月的发病数进行预测(图6)。再以2016年7-12月实际发病数为验证数据。结果可见，预测结果与实际情况的总体趋势一致，平均相对误差降低至18.12%，较之预测全年发病数相对误差明显减小，与ARIMA模型短期预测效果更好的特点相符。

图5 2016年1-12月朝阳区手足口病月发病数趋势预测图

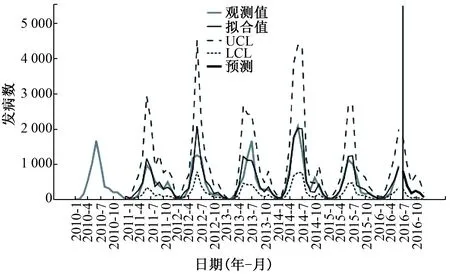
图6 2016年7-12月朝阳区手足口病月发病数趋势预测图

3 讨论

3.1此次拟合的ARIMA模型，预测手足口月发病趋势与实际发病整体变化趋势一致。适用于手足口病等具有季节性变动特征的传染病预测[9-11]。ARIMA模型通常用来处理平稳的时间序列，而传染病发病数据序列大多是非平稳的。因此，建模之前需对数据进行处理，以达到平稳化的要求。分析发现，朝阳区手足口病发病时间序列呈现出明显的季节性特征，且每个月之间发病数相差较大，是非平稳序列。因此，采用自然对数转换和季节性差分减少方差波动和实现序列平稳化。由于时间序列是根据事物发展的延续性而建立的，克服了影响预测对象的因素错综复杂、不易分析、数据资料不易获取等问题，以时间(t)综合替代各种影响因素，其模型构建短期精确度较高[12]。分析结果显示，对2016年全年(1-12月)和下半年(7-12月)的发病数据进行预测，实际发病数与预测发病数的平均相对误差分别为49.37%和18.12%。因此，在实际应用中，应动态开展短期预测，将新的实际发病数据纳入模型分析，从而提高预测精度，这也符合ARIMA模型依赖事物发展延续性的基本思想。

3.2ARIMA模型是依照事物发展的惯性趋势预测未来发病趋势的一种时间序列分析模型，而在实际中，影响手足口病发病的因素复杂且不断变化，如：易感者的数量、气候、病原谱的改变、手足口病防控工作的开展、疫苗的使用等均会对疾病的发展趋势造成影响[13-15]。但实际防病工作不能简单地依靠模型来判断，需要结合流行病学专业理论知识及发病影响因素进行具体分析，才能使模型预测在防控工作中发挥更大的作用。