不同坐标系向CGCS2000转换引起地块面积变化的研究——以镇江市为例

凌祥安，肖燕平，肖广新

(镇江市土地勘测事务所 测绘科，江苏 镇江 212000)

江苏省镇江市位于北纬31°37′—32°19′，东经118°37′—119°58′，东西最长直线距离95.5 km，南北最长直线距离76.9 km，市域面积约3 800 km2，平均海拔高程约20 m，为丘陵地区。

2000国家大地坐标系(China Geodetic Coordinate System 2000,CGCS2000)正式启用之前，镇江市存在多个坐标系共同使用的情况。多个坐标系共存，多套测绘成果并存，差异非常大。图件成果不能直接融合使用，必须经过繁琐的坐标转换，这给各类测绘成果的使用和管理带来了很多困难。

CGCS2000启用后，测绘成果必须基于CGCS2000，各类存量测绘地理信息数据必须向CGCS2000转换后使用，自然资源管理部门原有的地籍、耕地保护、土地利用、矿产管理等数据库也要转换到CGCS2000。同一地块的测量成果，采用CGCS2000椭球参数，不同的中央子午线的高斯投影坐标系，投影变形量不同，导致地籍管理的重要成果界址线长度、宗地面积存在差异。

地块面积是自然资源管理的重要内容，是资源管理、资产评估、税收的重要数据，地块面积的准确性关系土地所有者和使用者的切身利益。

分析地块在不同坐标系向CGCS2000转换后引起的面积变化，在自然资源管理工作中具有现实指导意义。

1 坐标转换引起地块面积变化的理论分析

根据《国土资源数据2000国家大地坐标系转换技术要求》《2000国家大地坐标系推广使用技术指南》，将国土资源各项调查、勘界、评价、资源管理等空间数据，遵循“应转尽转”的原则，转换为2000国家大地坐标系。

坐标转换通用流程如图1所示。将地方坐标通过高斯反算到大地坐标，利用同名重合点计算转换参数，采用一定的转换模型，将地方坐标的大地坐标或空间直角坐标转换为2000大地坐标或空间直角坐标，采用高斯-克吕格投影为2000平面直角坐标[1]169-172。

图1 坐标转换过程

1.1 自然资源管理工作主要使用的坐标系

自然资源管理系统依据不同业务建立的数据库采用多个坐标系。如镇江市城区地籍管理采用镇江地方坐标系(54椭球参数，投影中央子午线为119.5°)，所辖县级市句容、丹阳采用与城区相同的坐标系，扬中采用不同的坐标系(54椭球参数，投影中央子午线为120°)。耕地保护、土地利用规划、地质和矿产资源管理、地质环境管理、国土资源执法监察管理等数据库，其数据需上报自然资源部、省自然资源厅有关部门审核，由上级行政主管部门核查相关数据、下达用地指标，比例尺为1 ∶5000或1 ∶10000等中等比例尺，采用上级主管部门要求的坐标系(西安80椭球参数，中央子午线为120°，国家标准3度带投影)。还有个别项目采用投影中央子午线为120°的2000坐标系。表1为镇江市自然资源管理系统主要数据库使用的坐标系情况。

表1 镇江市自然资源管理系统主要数据库使用的坐标系汇总表

1.2 原椭球大地坐标转换为2000椭球大地坐标引起的面积变化

原椭球大地坐标转换为2000椭球大地坐标时需要选择模型。因为大地高程异常的存在，且在转换前后均采用同一高程系统，故转换模型不采用布尔沙模型，而选用二维七参数转换模型，公式为

(1)

ΔB，ΔL分别为同一点位在两个坐标系下的纬度差、经度差，Δa，Δf分别为椭球长半轴差、扁率差，ΔX，ΔY，ΔZ为平移参数，εx，εy，εz为旋转参数，m为尺度参数。

坐标转换为2000坐标引起的面积变化[2-3]

S2000=(1+m)2S原，

(2)

面积变化率

(3)

m是一个非常小的变量，实际计算中舍去m2。由公式(3)可知，坐标转换引起的面积变化率为一常数，等于两倍的尺度参数[4]。

1.3 高斯投影变形引起的面积变化

高斯投影变形有两种，即实际边长归算到参考椭球面引起的长度变形ΔL1和参考椭球面边长归算到高斯投影面引起的长度变形ΔL2[5]，

(4)

(5)

高斯变形引起的面积变化[6]

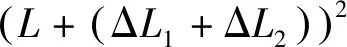
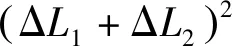
(6)

(7)

式(6)和式(7)中，ym为投影边两端横坐标平均值，Rm为参考椭球面平均曲率半径，Hm为投影边高出参考椭球面的平均高程值，R为投影边在参考椭球面上法截弧的曲率半径，L为归算边边长。同一地块由高斯变形引起的面积变化主要由高程、椭球曲率半径、地块到中央子午线的距离决定。面积变化与地块到中央子午线的距离成正比，即距离越远，面积变化越大。高程引起的面积变化是负值，地块高程越高，面积变化越大。

2 坐标系转换后面积变化量的实例分析

镇江市自然资源管理系统主要数据库使用的坐标系平面采用54或80椭球参数，中央子午线为119.5°或120°高斯投影，高程均采用85高程基准。为计算坐标系转换后面积的变化量，利用镇江市高等级GPS网控制点在不同坐标系中的坐标值，选取不同区域内相邻控制点组成12块分布较均匀的多边形地块，取地块中心点高程作为地块高程值，计算中心点到中央子午线的距离，从而得出地块高斯投影长度变形量。计算同一地块在不同投影中央子午线不同坐标系的面积值，分析坐标转换的面积变化。计算结果如表2所示。

1)投影中央子午线为120°时，大部分区域高斯投影变形超限。采用中央子午线为119.5°投影时(54椭球或2000椭球)，高斯投影带来的长度变形值均小于25 mm·km-1，满足《城市测量规范》《地籍调查规程》要求。采用中央子午线为120°投影(80椭球或2000椭球)时，高斯投影带来的长度变形值大部分区域不满足《城市测量规范》《地籍调查规程》“变形值不得大于25 mm·km-1”的要求，最大值为77 mm·km-1，如位于镇江市西部的句容市黄梅镇。因此，采用中央子午线为120°的高斯投影不适合作为全市统一数据库的测量基础，不能作为大比例尺测图或工程用。变形值超限时，可以选择将中央子午线移至能控制投影变形范围或重新设定高程抵偿面，使变形值符合规定。

2)同一坐标系内，地块离中央子午线越远，高斯投影长度变形愈大，面积变化愈大。2000坐标(120°)各地块距离中央子午线7～82 km，高斯投影变形为0～70 mm·km-1，同一地块从54坐标(119.5°)转换到2000坐标(120°)的面积变化率D4-1由1/119307到1/6094，从80坐标(120°)转换到2000坐标(120°)的面积变化率D4-2由1/365613到1/153657，从2000坐标(119.5°)转换到2000坐标(120°)的面积变化率D4-3由1/37407到1/7007。

3)到中央子午线距离相等时，高程对长度、面积变化有影响。2000坐标(120°)中，米芾广场地块和上党镇地块与中央子午线的距离相等，但投影长度分别为30 mm·km-1和33 mm·km-1，面积变化率也不同。高程变高，投影后长度变短，面积变小，地块归化到参考椭球面的改正数与椭球面归算到投影面的改正数符号相反，可以抵消一些误差。高程变化较大的区域，如山区、高原，选择独立坐标的精密测量工程项目，可以通过选择合适的高程抵偿投影面来减少高斯投影带来的变形。丘陵、平原等高程变化不大的区域，高程的影响不大。

4)高斯投影长度变形主要与中央子午线的选择有关。由同一地块从54坐标(119.5°)转换到2000坐标(119.5°)，从80坐标(120°)转换到2000坐标(120°)的高斯投影长度变形值可知，在投影中央子午线不变的情况下，采用不同椭球参数的坐标系内的高斯投影长度变形值一致。因此，选择相同的高程系统，投影面不变化时，不同椭球参数对高斯投影变形的影响很小。

5)在投影中央子午线不变的情况下，地块面积的变化仅与椭球的变化有关，即与坐标转换的尺度参数有关。不同地块从54坐标(119.5°)转换到2000坐标(119.5°)的面积变化率D3-1，最小为1/56757，最大为1/46785，从80坐标(120°)转换到2000坐标(120°)的面积变化率D4-2，最小为1/633232，最大为1/153657，面积变化率变化不大，基本为常数。表2中的面积变化主要由数学计算或控制点本身误差引起，这验证了公式(2)和公式(3)。

6)中央子午线的改变会使同一地块在不同坐标系内的投影面积发生较大改变。不同地块从54坐标(119.5°)转换到80坐标(120°)的面积变化率D2-1，最小为1/199352，最大为1/6346；从80坐标(120°)转换到2000坐标(119.5°)的面积变化率D3-2，最小为1/79985，最大为1/7343；从54坐标(119.5°)转换到2000坐标(120°)的面积变化率D4-1，最小为1/290946，最大为1/6094；从2000坐标(119.5°)转换到2000坐标(120°)的面积变化率D4-3，最小为1/56610，最大为1/7007，面积变化率变化不均匀，跳跃性很大。为了保证坐标系的延续性，最好保证高斯投影中央子午线的一致性。

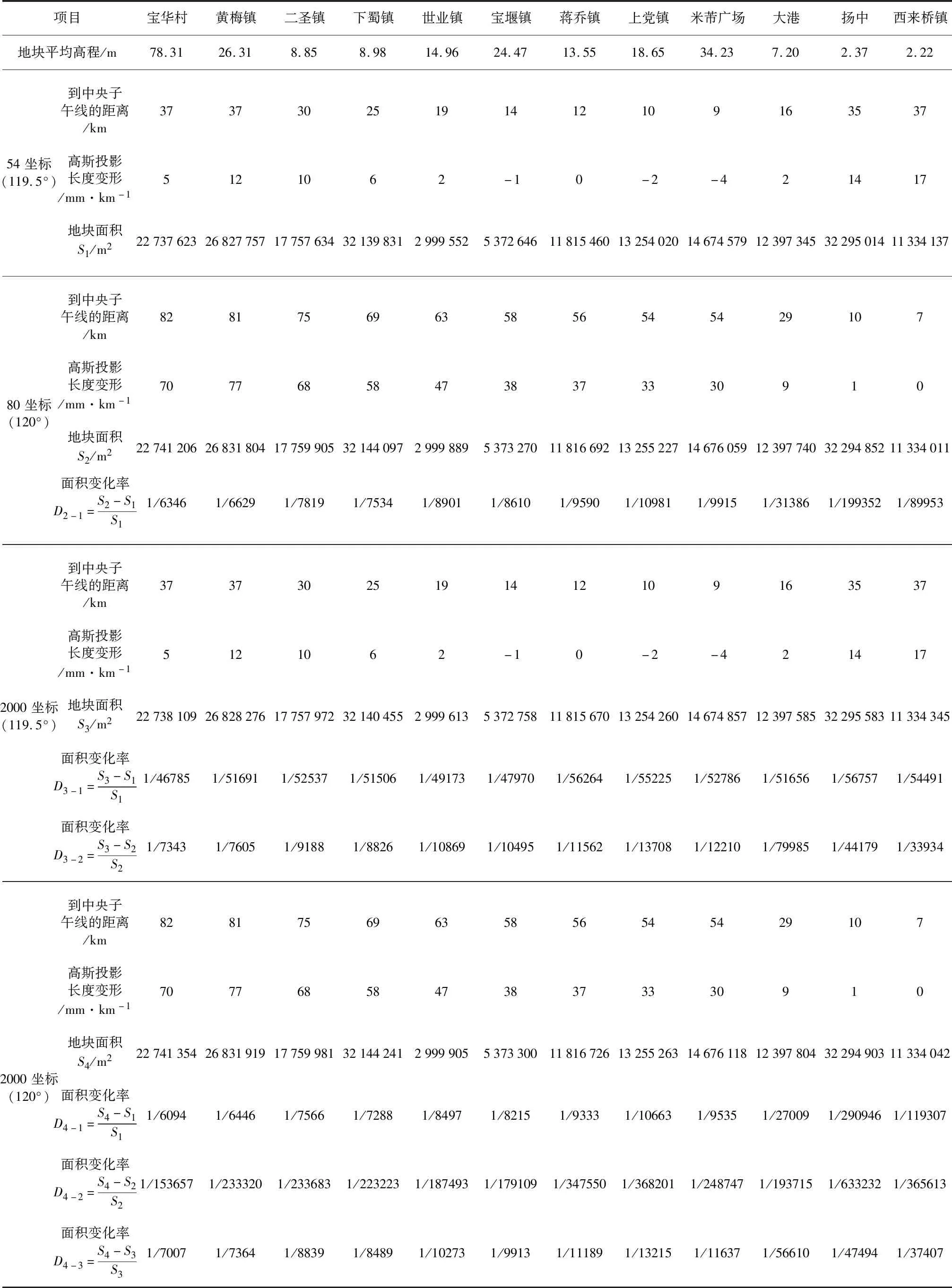
表2 坐标转换长度、面积变化计算表

3 结束语

考虑测绘资料的共享性、历史资料的延续性，减少坐标转换引起的长度变形和面积变化，坐标转换前后的中央子午线尽量保持一致。建议镇江市主管部门建立与原地方坐标系采用同一中央子午线119.5°的镇江2000地方坐标系，用于不动产发证、高精度地形图测绘等，满足大多数工程建设对坐标系的要求；耕地保护数据库、土地卫片执法数据库等转换为以120°为中央子午线的国家标准3°高斯正形投影CGCS2000，以满足部、省统一管理的要求。上报变更数据时，须向上级部门解释同一地块在不同坐标系下面积变化的原理、方法及其存在的必然性。