密封包装容器微环境温湿度模型的建立与仿真

李迪凡，王艳艳，李泽华，刘俊

（西南技术工程研究所，重庆 400039）

包装容器内装备等产品大多采用密封包装方式进行长期贮存，在其周围以及内部形成了一个相对密闭的空间，与贮存环境相对应，这一密闭空间称为微环境。在密封防护体系中长期存放的产品，微环境的温度和相对湿度将直接影响产品效应，使其性能发生显著变化。目前检测微环境温度和相对湿度的常用方法是将温湿度传感器置于包装容器内，而绝大部分包装容器一般没有预留检测小孔，在不破坏容器整体的情况下，无法将传感器置入容器内部。即使是无线传感器，但由于其电池使用寿命较短，无法长时间进行工作，也势必影响微环境温度和相对湿度的常规检测。因此传统的微环境温度和相对湿度检测方法弊端明显，需要耗费较长时间和较大经费。由于装备类产品的贮存时间较长，必须了解微环境温度和相对湿度的变化情况，以便掌握其贮存性能特征。目前缺乏正确的微环境温度和相对湿度仿真软件，无法获取装备在贮存环境下的微环境温度和相对湿度变化规律，不能满足装备类产品的发展需求。文中通过建立微环境温度和相对湿度模型，并利用相关软件对包装容器微环境的温度和相对湿度进行仿真，能在不破坏包装容器的情况下，实现对贮存环境条件下密封包装容器微环境温度和相对湿度的预计，解决密封包装容器微环境温度和相对湿度检测难题，对装备贮存使用和包装产品研制开发具有非常重要的实际意义[1-5]。

1 温度建模

1.1 建模理论

包装容器的温度模拟是基于传热学基本原理，即热量自发地从高温物体传向低温物体，或者从物体的高温部分传递到低温部分，因此温度建模同样遵守热力学第一定律、第二定律和热传导傅里叶定律。当包装容器在恒定温度和相对湿度的环境贮存时，热量的流动不随时间发生变化，热量传递处于稳态，容器的温度和热载荷不随时间变化。稳态传热的微分模型为：

式中：λxx、λyy、λzz分别为方向x、y、z 上的热传导率；T 为温度；分别为方向x、y、z 上的热梯度；内部热生成。

另一种是包装容器贮存环境的温度和相对湿度等要素不断地变化，热量的传递是瞬态的。对于某一特定条件下的解，需要给出定解条件，即初始条件和边界条件。瞬态传热的微分模型位：

式中：[λ]为传导矩阵，包含热系数、对流系数及辐射和形状系数；[C]为比热系数，考虑系统内能的增加；{T}为节点温度向量；为温度对时间的导数；{Q}为节点热流率向量，包括热生成。

1.2 有限元分析

利用ANSYS 作为温度模拟的分析软件，釆用SOLID70 作为热实体。该热实体具有八个节点，每个节点具有一个温度自由度，可以用于分析稳态或瞬态热问题，也可用于补偿因恒定速度质量输运带来的热损失。如果模型中间含有热实体传递结构单元，那么还需进一步进行结构分析，此单元可以被一个等效的结构单元所代替。此单元有一个选项用以模拟通过多孔介质的非线性稳态流动，原有的热参数可以被解释为相似的流体流动参数。温度有限元计算过程如图1 所示。

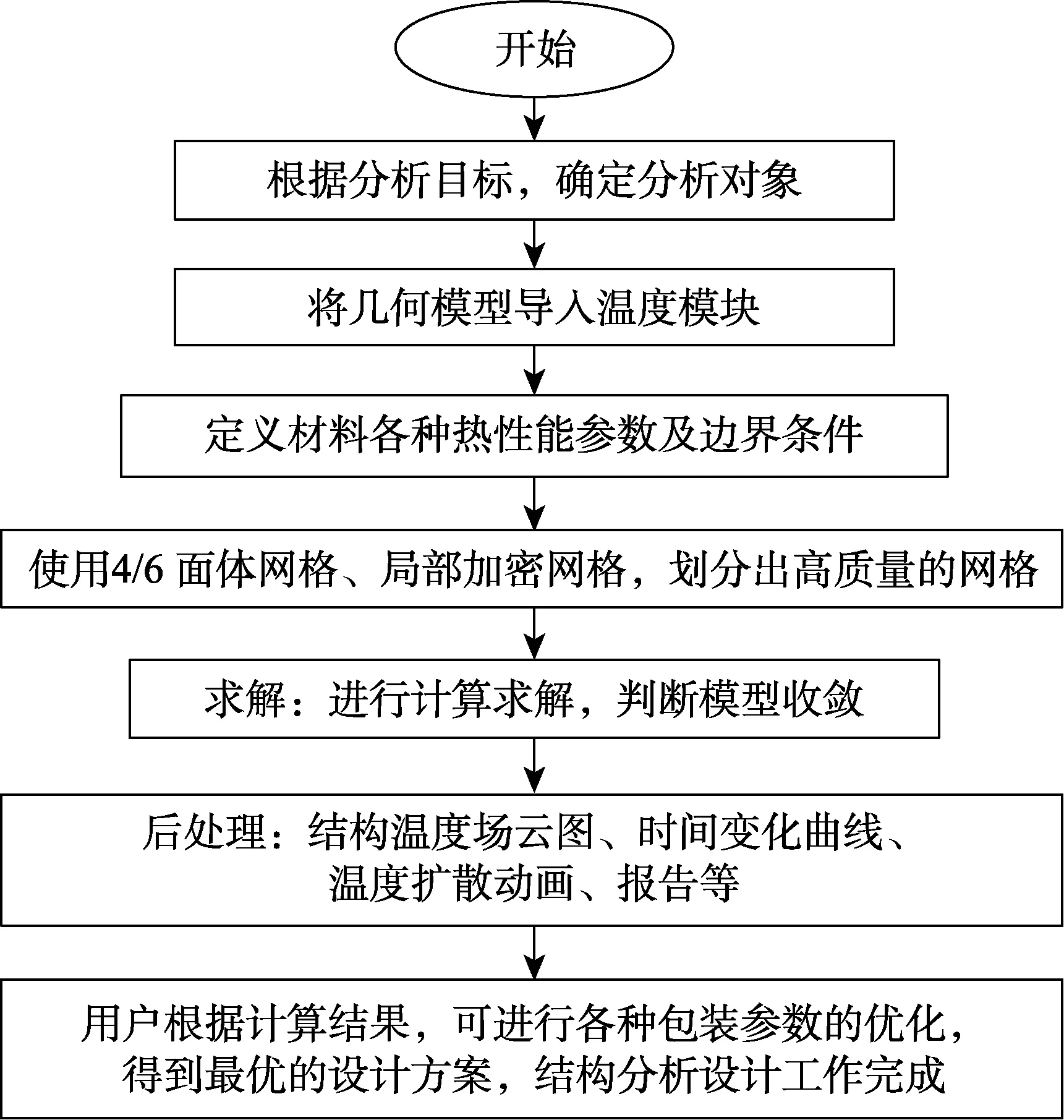
图1 温度有限元计算过程

2 相对湿度建模

2.1 建模理论

大多数的包装材料如工程塑料和复合材料等具有亲水性，容易吸收周围环境中的湿气，进入包装容器微环境，影响包装产品的可靠性。湿气可以通过扩散、压力驱动、表面张力等方式进入包装容器中，其中扩散是湿气传播的主要途径，遵循Fick 第二定律。当包装产品吸收潮气的时间过长，使包装材料的性质退化，甚至出现很大膨胀时，湿气扩散才不完全遵守Fick 扩散定律，需要对其进行修正，湿气扩散方程为：

式中：RH 为相对湿度；D 为材料湿度扩散系数（需要根据现有包装材料试验结果确定）。

展开得：

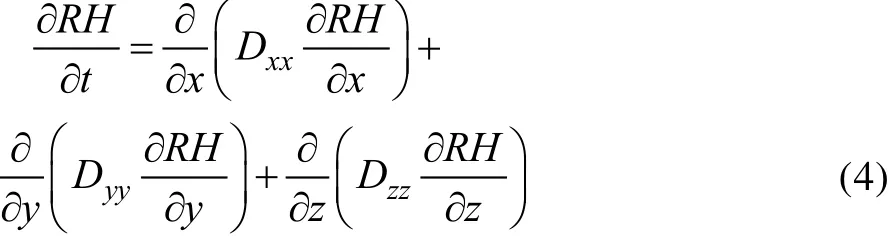
假设包装材料内部为各项同性， 则有Dxx=Dyy=Dzz，得：

通过对式（5）进行求解，即可得出包装材料内部随外部相对湿度、时间的变化趋势。

通过分析发现，热传导方程和湿气扩散方程在形式上是相同的。通过将热传导方程中的温度T 和热传导系数k 替换成湿度C(x,y,z)和湿度扩散系数D，就可以采用有限元软件的热传导模块进行湿气扩散分析模拟[6-14]。

2.2 有限元分析

通用大型有限元分析软件通常没有专门的湿气扩散分析模块，利用相对湿度的处理方法，可以通过湿热之间的对比关系，使用通用有限元分析软件的热分析模块来进行湿气扩散的有限元分析，各参数对应情况见表1。相对湿度有限元计算过程如图2 所示。

表1 湿度扩散分析与热分析变量对应关系

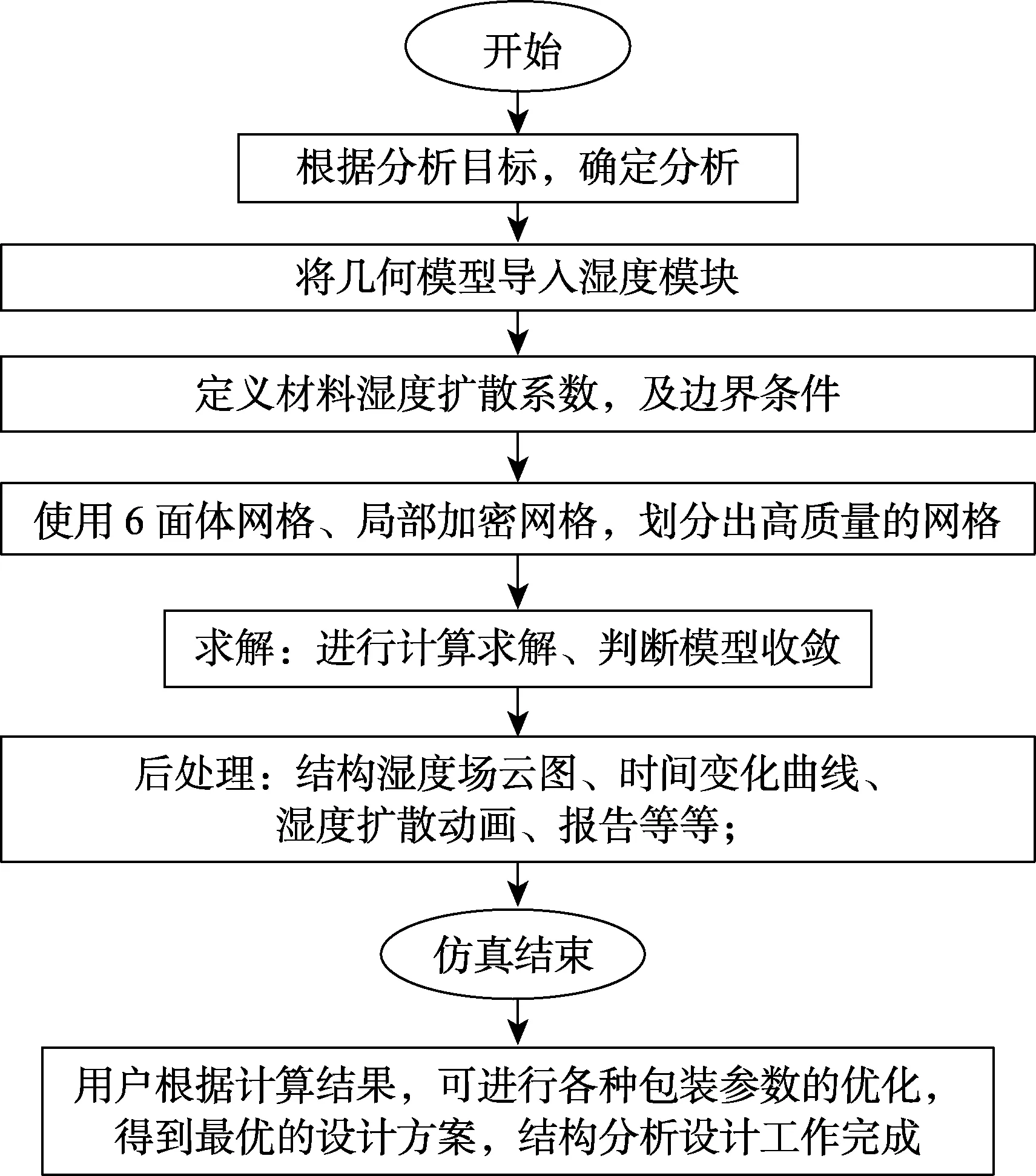
图2 相对湿度有限元计算过程

3 试验与仿真

3.1 试验样品

以密封包装容器为研究对象，建立有限元模型，模拟在外部载荷作用下包装容器微环境的温湿度场。试验样品由3k 碳纤维布和环氧树脂等材料组成，容器壁厚为2 mm，包装容器内径为95 mm、长位800 mm，形状为圆柱体。两端盖为铝合金，用硅胶进行密封。研究某典型气候试验站投样后，包装容器环境温湿度和微环境温湿度变化情况。采样时间为2016 年4 月18 日0点08 分至2016 年04 月20 日18 点38 分，采样间隔为10 min/次，一共提取了400 个测点的数据。

3.2 仿真

根据包装容器结构特性，开展有限元模型研究，温度模拟的几何模型如图3a 所示，有限元模型中需要确定内部空气、包装材料、铝合金三种材料的物理性能，如密度、热传导系数和比热。温度预测的初始条件为2016 年4 月18 日0 点08 分的初始温度场，通过有限元法稳态温度场分析得出（如图3b 所示）。边界条件为试验测试得到的该时间段内环境温度随时间的变化曲线，仿真的最终温度场结果如图3c 所示。

相对湿度建模参照温度建模方式进行，确定材料的密度、湿度扩撒系数和比热等物理参数，建立的相对湿度模拟的几何模型如图4a 所示。以2016 年4 月18 日0 点08 分的初始湿度场为初始条件，如图4b所示。以试验测试得到的该时间段内环境相对湿度随时间的变化曲线为边界条件进行仿真，最终湿度场模拟结果如图4c 所示。

3.3 结果分析

结合建立的仿真模型，以及利用试验测试结果，对包装容器微环境温湿度的变化情况进行模拟仿真，其仿真结果如图5 所示。

从图5 中可以看出，试验测试结果和仿真结果的规律相同，二者的变化趋势吻合得很好，相对湿度随着时间以天为大周期变化。试验测试结果包含更多的环境及测试因素的影响，所以相对湿度曲线有更多的噪声，而模拟结果则更加光滑。对微环境仿真值与实测值之间的误差进行分析，温度的最大相对误差不超过8%，相对湿度的最大相对误差不超过11%。

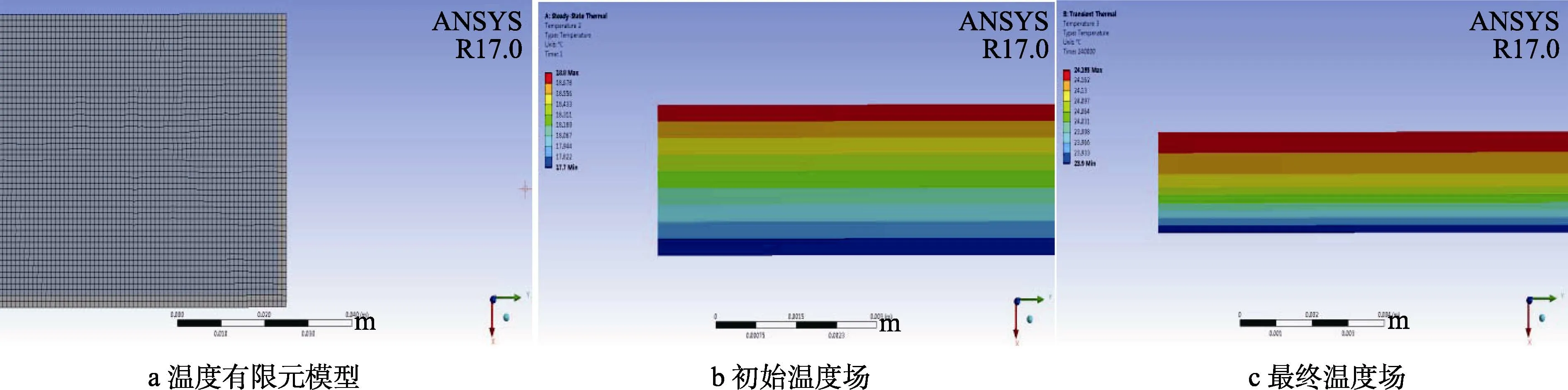
图3 温度模拟

图4 相对湿度模拟

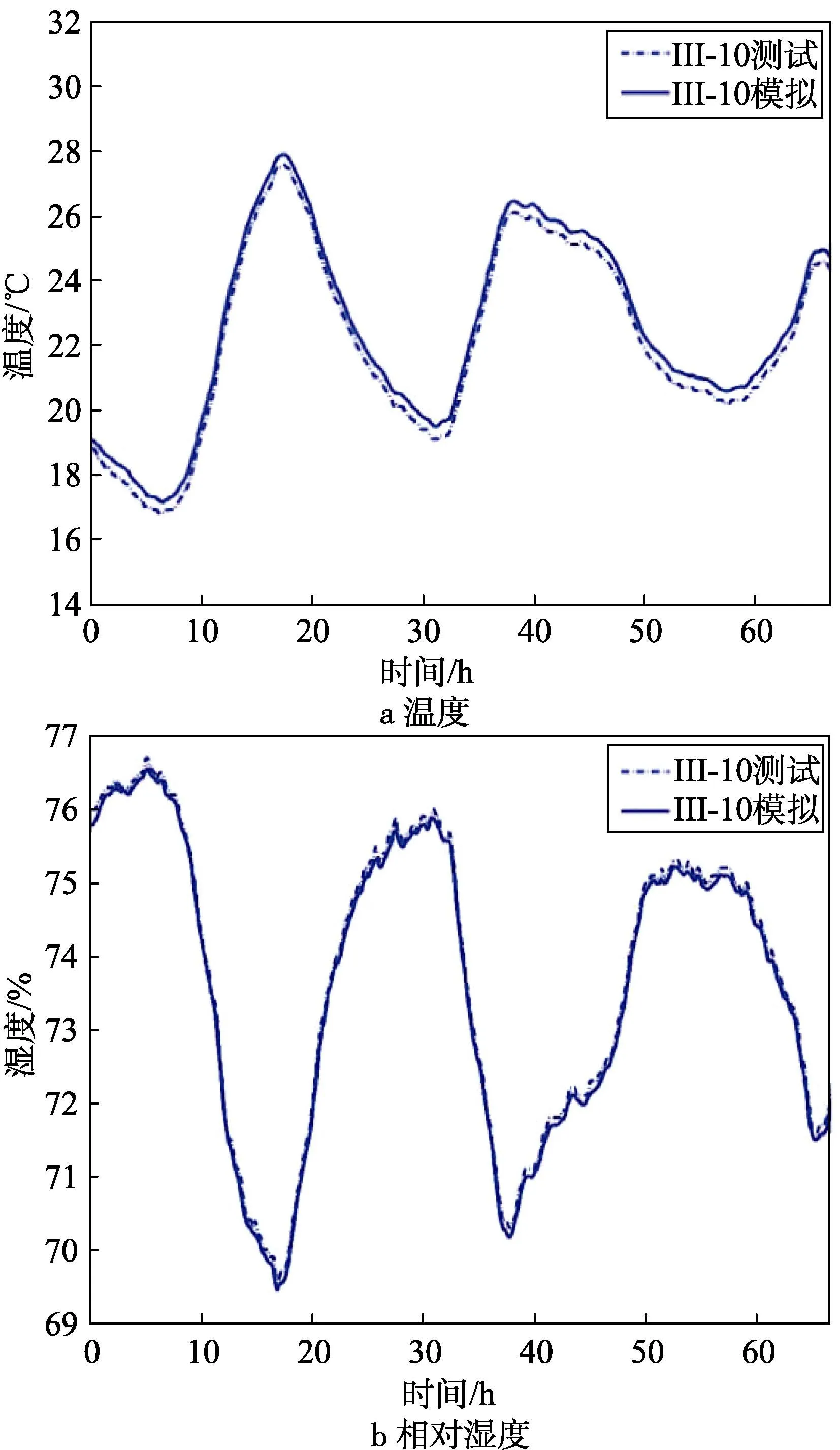
图5 仿真结果

4 结语

通过获取的大量密封包装容器在不同环境下的贮存试验数据，对建立的包装容器微环境温度和相对湿度模型进行了反复校验和修正，保证了模型的准确性。建立的微环境温湿度仿真软件能对贮存时间较长、不同规格的密封包装容器温湿度进行准确仿真，可以避免包装容器类产品自然环境试验的高费用和长时间，为寻找环境失效的原因和机理、确定合理科学的维修时间和内容、优化贮存使用方法提供了重要的数据支撑，具有良好的应用前景。