基于遗传算法的变速风电机组传动链加阻器自整定
2019-08-20万宇宾刘红文蒋韬胡婵娟
文 | 万宇宾,刘红文,蒋韬,胡婵娟
对于采用“增速齿轮箱+高速发电机(双馈或高速永磁)”传动链形式的风电机组,其传动链一阶扭转振动模态的固有阻尼通常较低,在机组发电运行过程中(特别是在恒转速运行区段),当风速变化较快或穿越电网故障时,传动链模态可能受到较强的激发。在发电机转矩指令中叠加一个变化的分量可使传动链模态的等效阻尼得以提升,从而有效抑制扭振、降低疲劳载荷,此项技术被称为传动链加阻,目前已广泛应用于兆瓦级风电机组。
经典的加阻器结构较简单(通常为一个含超前补偿的带通滤波器),参数整定难度不大。但近年来,随着风轮直径和塔架高度的不断增加,与传动链模态耦合的风轮面内模态和塔架侧向模态变得更易于激发,需要重点关注。此外,为降低度电成本,面向特定场址的精细化、定制化设计逐渐成为常态,这使得风电机组对于工程不确定性的容纳能力在客观上呈下降趋势。上述背景下,设计者须对加阻器作更为精细的设计和调节,以充分抑制传动链及其耦合模态的激发,经典的加阻器结构往往难以提供最优的加阻性能,采用相对复杂的加阻器结构可更好地逼近最优,但其参数数量及整定难度也相应增加,采用手动整定时,对工程师的经验和设计水平有更高的要求,设计质量相对难以保证。
针对上述情况,本文提出一种基于自适应遗传算法的传动链加阻器自整定框架,该框架考虑了几种典型的加阻滤波器结构,允许利用先验信息和参数物理意义施加约束,并根据期望的时、频域指标定义了适应度函数,利用遗传算法的寻优能力实现加阻器参数自整定。
传动链加阻器自整定框架
一、传动链加阻基本原理
传动链加阻技术的基本原理可表述为:通过设计适当的加阻器(DTD),从发电机转速测量值中提取扭振速度分量,并据此构造一个与扭振速度相位相近、幅值成正比的传动链加阻转矩分量,叠加到转矩指令中,使得闭环系统中传动链模态的等效阻尼得以提升。控制结构如图1所示,其中,、ωgen为发电机转速指令和反馈,、为发电机转矩指令的PI分量和加阻分量,Ta为气动转矩。
传动链加阻器的手动整定多采用极点配置,一般应符合以下原则:
(1)在待加阻频率附近具有较高的增益,以实现足够的加阻;
(2) 在低、高频段具有相对较低的增益,避免引入不期望的功率波动或噪声;
(3)在待加阻频率附近具有接近0度的相移。
二、典型加阻滤波器结构
工程上常用的加阻滤波器包括但不限于以下形式:
1.单一带通滤波器(BPF)
二阶带通滤波器传递函数如下:


图1 传动链加阻控制结构

图2 基于单一带通滤波器的传动链加阻器
式中,K为加阻增益,ζ为阻尼,ω的取值应接近未加阻时的自然振荡频率,τ用于调整相移、补偿时延和改变滤波器特性。
2.多个带通滤波器并联
这种结构适用于需对多个相隔较远的模态同时进行加阻的情况,每个带通滤波器的频率取值应分别接近这些模态。
3. 带通滤波器与带阻滤波器(Notch)串联
相对于前面两种,这种结构的特点在于其具有更高的设计自由度和更丰富的幅频特征表达能力,理论上可实现更优的加阻性能,但由于其参数数量较多,且取值与模态频率无明确的对应关系,参数整定相对较困难。二阶带阻滤波器传递函数如下:
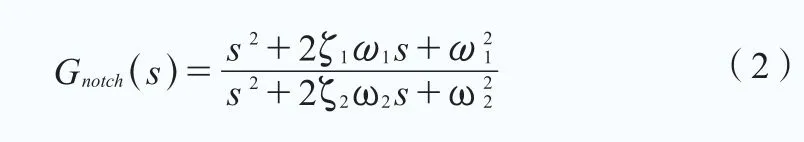
三、自适应遗传算法
1. 自适应遗传算法简介
遗传算法(GAs)是一类模拟生物进化过程的全局优化算法。在其优化过程中无需对目标函数进行反演,也不要求目标函数可导,对各类优化问题具有广泛的适应性。作为遗传算法的主要操作算子,交叉和变异在很大程度上决定了GAs的搜索特性。在简单遗传算法(SGA)中,交叉概率和变异概率取常数,难以在搜索效率和避免局部最优间取得平衡。针对SGA的不足,Srinivas等人提出自适应遗传算法(AGA),AGA在SGA基础上加入了交叉、变异概率的自适应律,既保持了启发式搜索的效率优势,也使种群得以维持一定的多样性。
对于上文介绍的几种加阻器结构,除单个带通滤波器较简单外,其余类型均需整定较多参数,搜索空间维度较高,同时期望算法尽可能避免陷于局部最优,故选择AGA作为自整定框架的优化算法。
2. 约束设计
合理利用先验信息和参数物理含义施加约束可显著缩减搜索空间。具体而言,结合兆瓦级风电机组的典型模态频率,滤波器频率参数ω的搜索范围可限定于5~25 rad/s,当ω与模态频率存在明确对应关系时(例如:并联的多个带通滤波器),可直接指定ω数值从而降低搜索维度,也可将ω的范围限制在模态频率附近;根据物理含义,所有滤波器阻尼参数ζ限定于0.05~0.95;考虑典型转矩指令、速度反馈传输时延,所有时间常数τ限定于0.01~0.07 s;根据一般经验,增益参数搜索范围可限定于10~1000。以上约束设计适用于本文选取的设计对象,对于其他机型可作适当调整。此外,施加更精准的约束有利于进一步缩短参数自整定过程,但可能并非必要。
3. 适应度函数设计
遗传算法中,适应度函数用于个体的性能评价,并直接决定了优化的倾向。针对加阻器参数整定及优化设计目标,选取低速轴转矩对发电机转矩指令的阶跃响应为主要考察对象,提出以下2种适应度函数:
(1)低速轴转矩变化率绝对值积分,其离散形式可写为:

(2)时间加权低速轴转矩变化率绝对值积分,其离散形式可写为:

以上两式中,n为阶跃响应的采样点数,Tor为低速轴转矩采样值,t为时间采样值。
在适应度函数中需要体现的其他限定条件以惩罚形式实现。当加阻器开环幅频特性高、低频段增益高于预设值,以及加入加阻器后系统增益裕度、相角裕度低于预设值时施以惩罚,即:

式中,cost为预设的惩罚值。
参数整定测试及评估
以某型2MW双馈机组为原型进行加阻器自整定及对比评估,机组在16m/s风速下的传动链及耦合模态信息如下:
考虑2种适应度函数、3种加阻器结构,在Matlab环境下进行加阻器自整定测试,将整定结果用于传动链模型,结合加阻器开环特性、加阻前后传动链系统开环特性、加阻前后低速轴转矩对发电机转矩指令阶跃响应对加阻器性能进行评估,遗传算法种群个数取100,精英个数取2。

图3 基于多个带通滤波器并联的传动链加阻器
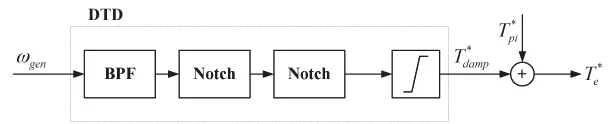
图4 基于带通滤波器与带阻滤波器串联的传动链加阻器
一、情况1:单一带通滤波器,IAR,待整定参数4个
最优个体适应度为711.8255,对应参数:
K=591.5795;ω =7.9809;ζ=0.3721;τ=0.0501
具体结果如图5所示。
二、情况2:多个带通滤波器并联,IAR,待整定参数12个
最优个体适应度为529.6658,对应参数:
K1=613.3398;ω1=7.2499;ζ1=0.2777;τ1=0.0169
K2=281.5164;ω2=16.4169;ζ2=0.7114;τ2=0.0102

表1 原型机模态信息

图5 情况1整定结果(左上、右上、左下、右下依次为:遗传算法进化曲线、加阻器开环特性、加阻前后传动链系统开环特性、加阻前后低速轴转矩对发电机转矩指令阶跃响应,图6-图7类同)
K3=766.3081;ω3=17.8995;ζ3=0.1327;τ3=0.0132
具体结果如图6所示。
三、情况3:带通滤波器与带阻滤波器串联,IAR,待整定参数12个
最优个体适应度为481.9224,对应参数:
K= 937.4840;ω =9.5624;ζ=0.8524;τ=0.0116
ω1A=11.5252;ζ1A=0.6784;ω2A=24.3169;ζ2A=0.2117
ω1B=119.9109;ζ1B=0.7387;ω2B=8.7462; ζ2B=0.7934
具体结果如图7所示。
四、情况4:单一带通滤波器,ITAR,待整定参数4个
最优个体适应度为2247.2103,对应参数:
K= 443.6622;ω =12.9089;ζ=0.9145;τ=0.01579
图示从略。
五、情况5:多个带通滤波器并联,ITAR,待整定参数12个

图6 情况2整定结果
最优个体适应度为1008.3327,对应参数:
K1=488.4967;ω1=8.2298;ζ1=0.3255;τ1=0.0150
K2=184.9247;ω2=16.3280;ζ2=0.5651;τ2=0.0102
K3=692.6088;ω3=17.1328;ζ3=0.0577;τ3=0.0692
图示从略。
六、情况6:带通滤波器与带阻滤波器串联,ITAR,待整定参数12个
最优个体适应度为999.2987,对应参数:
K= 964.8767;ω =11.0582;ζ=0.4080;τ=0.0201
ω1A=19.1263;ζ1A=0.9062;ω2A=12.3245;ζ2A=0.7058
ω1B=11.9740;ζ1B=0.0657;ω2B=18.1132;ζ2B=0.2277
图示从略。
七、对比分析
表2对各种情况下的传动链系统开环幅频特性进行了汇总,可见:
(1)6种情况下的整定结果均可实现对传动链模态的有效加阻,传动链模态由加阻前的78.6dB降至50dB左右,满足基本设计要求;
(2)关于适应度函数:对于传动链模态,IAR指标(情况1—3)下的抑制效果略优于ITAR指标(情况4—6);对于风轮面内和塔架侧向模态,则恰恰相反,ITAR指标较优。对上述结果的合理解释是:IAR不考虑时间加权,因此该指标更倾向于抑制波动量值上占主导影响的传动链模态,对于风轮面内、塔架侧向模态的抑制则有所忽略甚至牺牲;ITAR指标引入了时间加权,对阶跃响应的后期给予了较高的权重,因此更有利于实现对各模态的均衡抑制;
(3)关于加阻器结构:可以看出,在IAR、ITAR两种指标下,单一带通滤波器(情况1、4)均难以实现对风轮、塔架模态的有效抑制;带通滤波器并联结构(情况2、5)与带通带阻串联结构(情况3、6)的表现基本相当,且均优于单一带通滤波器,能较好地兼顾传动链、风轮、塔架模态的抑制。

图7 情况3整定结果
结论
传动链加阻器参数自整定框架将繁琐的人工调节工作转化为对性能指标及约束条件的规划设计,具有较好的应用价值。基于本文参数整定测试及评估结果,可得出以下结论:
(1)对于相同的适应度指标,一般而言,结构较复杂的加阻器可实现更优的加阻性能,这在很大程度上得益于其更强的频率特性表达能力;
(2)对于相同的加阻器结构,适应度函数的构造对于优化结果有较大影响,IAR指标偏重于阶跃响应的前期快速收敛,但对于耦合模态的加阻性能相对较差;ITAR指标可较好地兼顾各个模态的加阻,对加阻器设计的适应性更好;
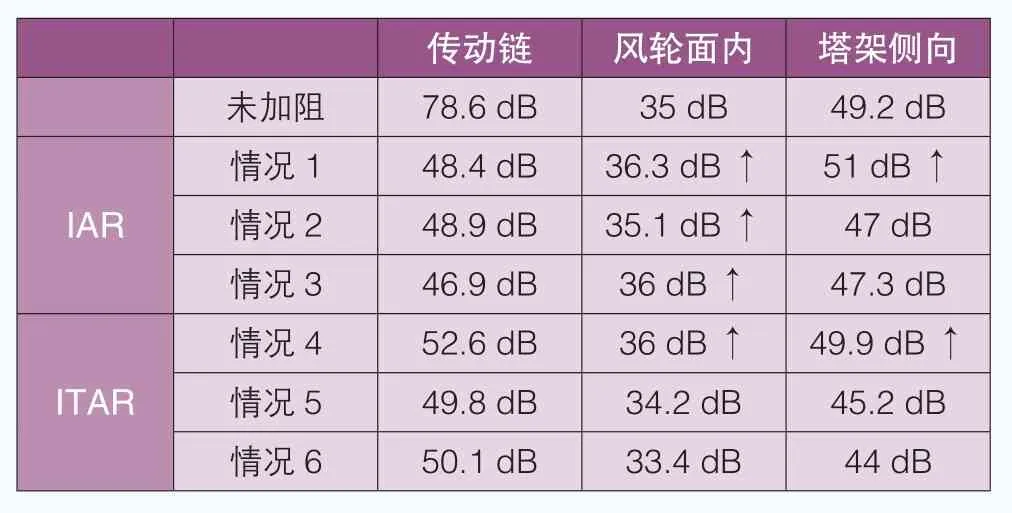
表2 传动链系统开环幅频特性对比
(3)本文研究工作局限于模型精确已知条件下的离线参数自整定,如何将该框架在线地应用于存在参数不确定性的实物机组,仍是值得进一步研究的课题。
