基于MDP的血小板库存最优订货策略和使用策略研究

李 猜， 耿 娜， 王春鸣

(1.上海交通大学 工业工程与管理系，上海 200240； 2.上海交通大学 中美物流研究院，上海 200030; 3.上海交通大学 医学院附属仁济医院，上海 200127)

0 引言

血液是一种特殊的稀缺资源，主要有以下五个特点：(1)血液产品属于易逝品，有一定的保质期，一旦过了保质期就不能再用于输血；(2)供给相当不规则，因为血液产品的供给完全依赖于献血者捐献；(3)需求随机且分类，一般可分为普通需求和紧急需求，普通需求可积压(部分手术可择期)，紧急需求不可积压；(4)普通需求的积压成本相对较低，紧急需求的缺货成本相对较高，需要通过高成本的紧急采血或者临时调配进行处理，否则患者可能有生命危险；(5)过期不容易被接受，因为不仅要避免稀缺资源的浪费，还要考虑献血者的心情，尊重献血者的贡献。因此，血液产品的库存管理一直是易逝品库存研究的热点和难点[1,2]。血液产品中血小板保质期较短，为5到7天，从采集到检测一般需要2天，供给医院可使用的有效时间只有2～3天。输血时血小板的新鲜度对患者的健康会产生不同影响，Joyce等[3]和Keuren等[4]发现输注1～3天的新鲜血小板比较好，4～5天的血小板被认为随着血小板的寿命变化，可能产生被认为是有害的物质。根据Eder等[5]，85%的败血症输血反应发生在输血年龄为第四天或者第五天的时候，时间越长，风险越大。Haijema[6]和Kort等[7]认为输注更新鲜的血液更有效。美国近期发布的输血服务指南草案已经提出尽量减少输注第四天或者第五天的血小板的比例，但是并非强制执行[2]。血小板的库存管理除了考虑传统的平衡浪费和短缺成本进行订货决策外，还需要考虑血小板输注时的新鲜度对患者健康的影响进行使用策略(Issuing policy)决策。订货策略确定每次补充的新鲜血小板的数量，使用策略确定输注血小板时不同新鲜度血小板的使用顺序。因此，本文主要针对血小板库存管理中的两个问题，即订货与使用策略，进行研究。

血小板的库存管理在理论与实践中都是非常具有挑战性的，实践中常用的订货策略多为基于经验的阈值策略，即每次都补货到一个经验库存水平；血小板的使用策略上，由于血液资源的稀缺性，医院为了避免浪费，一般会选择先用陈旧血小板(First In First Out, FIFO)的使用策略。对于血小板的订货和使用策略，订货过多会造成不必要的浪费，订货过少会产生短缺。使用FIFO策略会减少短缺和浪费，但会降低平均输血新鲜度(即增加平均输血年龄)；新鲜血小板先用(Last In First Out, LIFO)的策略可以提高平均输血新鲜度(即减少平均输血年龄)，但会增加短缺和浪费。订货策略和使用策略之间会产生相互影响，订货策略不同会影响库存中新鲜血小板量从而影响使用策略；使用策略不同会影响库存中不同剩余寿命(Shelf life)血小板的分布状态，进一步影响订货策略。为了优化血小板的库存管理，本文通过构建有限时域的马尔科夫决策(MDP)模型，考虑需求随机到达，以效用最大化为目标，探讨血小板的最优订货和使用策略，以尽可能减少短缺和浪费并提高平均输血新鲜度；通过对最优策略数值解的观察，提出近似的启发式策略，并通过数值实验验证其性能。

1 文献综述

广义上来说，本文属于易逝品库存的范畴，需要进行分年龄库存管理。早期易逝品库存文献多关注以最小化短缺和浪费为目标的订货策略。如Nahmias[8]利用动态规划对提前期为0且寿命为m的易逝品的最优订货问题进行了详细的分析，但m较大时会引起“维度诅咒”(Curse of Dimension)，导致模型难以求解。后来的学者开始考虑用启发式算法或者仿真方法来研究问题，如Nahmias[9]考虑使用启发式方法对易逝品订货的动态规划模型进行近似求解。传统的易逝品库存问题一般假设物品效用与寿命无关，即只要物品没有过期，其效用就是固定的[10]。易逝品的使用策略一般会根据特定研究对象来确定，比如超市中的易逝品使用策略一般取决于顾客行为特征，对于一些保质期较短的产品顾客一般倾向于拿最新鲜的，而对保质期稍长的产品则可能会随机选取。

血液库存问题的研究是从20世纪60年代开始的，在20世纪70年代末和80年代达到顶峰，然后显著下降[11]。早期的研究多数针对全血，近期的文献则更多关注红细胞，针对血小板的库存管理文献相对较少。就研究方法而言，最常见的研究方法是动态规划和计算机仿真技术，还有少量文献采用排队论方法。Haijema等[12]结合随机动态规划和仿真提出了一种新的多步骤的启发式方法来解决血小板的订货问题，寻找近似最优的订货策略，结果发现简单的阈值订货策略几乎保持最优。Asllani等[13]将一个基于仿真的决策支持系统用于单采血小板的库存管理，减少了单采血小板的浪费。Civelek等[14]假设血小板补货的提前期为0，提出了一种针对血小板库存的双重补货策略。双重补货主要是指每天早上一个固定订货量的订单，然后当天其他时间根据需求选择是否需要增加快速补货订单。作者发现在正常订单之间增加快速补货订单可能是管理血小板库存的有价值的实践。普通补货策略主要关注短缺和浪费之间的平衡，双重补货则侧重于快速补货的成本和便利性。

绝大多数研究使用策略的文献还停留在一些简单的启发式策略比较的层面上。使用策略不仅会影响输血时血液新鲜度，还会影响剩余库存的年龄分布，进一步影响过期和短缺率。Keilson[15]比较了固定寿命易逝品库存系统在泊松供给和泊松需求下的FIFO和LIFO使用策略的性能，发现FIFO策略最小化了短缺和浪费但最大化了平均使用年龄，LIFO策略最小化了平均使用年龄但最大化了短缺和浪费。Atkinson等[16]针对红细胞的使用提出了一种结合FIFO和LIFO的阈值策略，通过仿真求出该策略的短缺率和平均使用年龄，发现该阈值策略比FIFO策略的性能要好。

通过建模优化使用策略的文献较少，Pierskalla[17]通过建立数学模型研究了易逝品库存的最优使用策略，但是该模型中的库存不会过期，只会恶化。Li等[18]在未过期库存收益相同的假设下证明了易逝品库存的最优使用策略是FIFO策略。

目前考虑输血时血液新鲜度进行库存优化的文献较少[6,19,20]。Haijema[6]研究了失销情况下易逝品的订货、使用和临期处理问题。该文献中使用策略仅考虑了FIFO和LIFO两种情况，订货策略和临期处理决策通过MDP模型来进行研究，目标是最小化短缺、浪费以及临期惩罚成本。模型假设提前期大于0小于1，将订货决策和临期处理决策分到两个时间段以避免高维度的决策空间，发现最优的临期处理决策对库存管理的改进可能有实用价值。Tetteh[19]认为输血的收益跟血小板输注的新鲜度有关，在供给和需求确定的情况下通过仿真来比较FIFO、LIFO以及FIFO和LIFO混合策略的浪费、短缺以及平均使用年龄。Slofstra[20]研究了实际供给和实际需求下红细胞的使用策略，构建了一个有限时域的MDP模型，以短缺、浪费以及年龄惩罚(越新鲜的血液惩罚成本越小)三种成本构建目标函数，分别在失销和积压的情况下进行求解。由于红细胞的寿命较长(42天)，模型状态空间较大，作者仅求解了单周期成本函数的短视策略。此外，该论文考虑了几种简单但是便于实施的使用策略，包括FIFO、LIFO、随机策略以及几种不同的阈值策略，并通过仿真比较以上这些使用策略的性能，找到每个成本参数集对应的表现较好的使用策略。

2 问题描述与MDP模型

2.1 问题描述与符号定义

本文针对医院血小板库存系统建立了有限时域的马尔科夫决策模型，研究不确定需求下系统的最优订货策略和使用策略。医院血小板的订货提前期为1天[12]，系统每天天初收到前一天的订货，更新系统状态并发出新一天的订单(订货决策)，在当天需求到达之后确定满足需求时不同剩余寿命血小板库存的使用量(使用决策)，并在天末丢弃过期的血小板。为了建立模型，本文做出以下假设：

假设1本文针对某一特定血型的血小板，假设血小板在医院的有效使用时间为2天。

假设2血小板补货的提前期为1天[12]，即第t天初下订单，第t+1天初即可到货。

假设3本文2.2与2.3节先后分别考虑可等待的普通需求(未满足积压)以及不可等待的紧急需求(未满足失销)，假设新的需求到达随机，需求量服从某一已知分布。

假设4为了避免浪费与打击献血者的积极性，假设库存与积压不会同时存在。

关于血小板输注血型问题的说明如下：根据临床输血技术规范[21]第十六条规定，输注手工分离浓缩血小板的患者输注前应进行交叉配血试验，输注机器单采浓缩血小板应ABO血型同型输注。交叉配血实验是为了在血型鉴定的基础上进一步确保输血安全，保证供血者与受血者之间不存在血型不合的抗原-抗体反应(人类的血型很复杂，即使是同型血之间还存在亚型的区别)。目前国内的临床输血规范[21]中并未涉及血小板的ABO相容性输注，而部分发达国家的血小板输注指南则基本包含了血小板相容性输注规则，允许当ABO血型相合血小板供不应求时，可以输注ABO血型不同的血小板[22]。国外大多数研究血小板库存的文献均未区分血型[6,7,12,14,19,23]，一般假设满足需求时首先使用最老的同型血，同型血不足时再按照血型相容性顺序选择其他可用血型。国内临床输血规范[21]中虽然没规定血小板的ABO相容性输注，但是临床输血实践证明输注ABO血型不相同的单采血小板对于挽救急性血小板减少引起的危及生命的出血患者可以取得良好的临床效果[22]。考虑到国内血小板ABO相容性输注存在争议，本文在假设1中假设模型针对某一特定血型的血小板进行研究。

由于血液中心的非盈利性，本模型忽略医院订购血小板的订货成本。另外在血液产品库存问题中，库存持有成本与浪费成本和短缺成本相比可以忽略不计[23]。因此模型的目标函数中仅考虑积压成本、失销成本、浪费成本以及不同剩余寿命血小板的输血效用。模型的符号定义如下：

2.2 面向普通需求的血小板库存管理MDP模型

本节面向普通需求，考虑需求在得不到满足的情况下可积压或延迟满足，对血小板进行库存控制研究。本模型的决策阶段为天数t，系统状态为(x1t,x2t)，x2t代表新鲜库存量，x1t≥0时代表陈旧库存量；x1t<0时代表积压的普通需求。每个阶段的决策分别为qt和yit。考虑积压成本、浪费成本和不同剩余寿命血小板的输血效用，可得普通需求阶段效用函数：

(1)

(2)

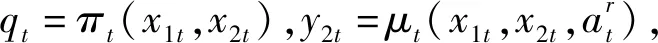
(3)

可建立普通需求下系统的目标函数为式(4)～(5)所示：

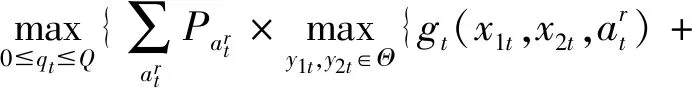
Vt+1(x1(t+1),x2(t+1))}}

(4)

VT(x1T,x2T)=0

(5)

其中第t天到第t+1天的状态迭代关系如下：

(6)

x2(t+1)=qt

(7)

2.3 面向紧急需求的血小板库存管理MDP模型

本节面向紧急需求，考虑需求必须尽快满足不能积压，在得不到满足的情况下只能失销，建立MDP模型，对血小板进行库存控制研究。该模型的系统状态和决策变量同普通需求，因为紧急需求下需求不会积压，因此，存在x1t≥0。考虑失销成本、浪费成本和不同剩余寿命血小板的输血效用，可得紧急需求下的阶段效用函数：

(8)

(9)

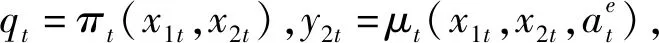
(10)

可建立紧急需求下系统的目标函数为式(11)～(12)所示：

Vt+1(x1(t+1),x2(t+1))}}

(11)

VT(x1T,x2T)=0

(12)

其中第t天到第t+1天的状态迭代关系如下：

x1(t+1)=x2t-y2t

(13)

x2(t+1)=qt

(14)

3 数值实验

本文2.2与2.3节提出的两个MDP模型多维度的状态空间使得最优控制策略结构特征的证明非常困难。当状态空间较小时，MDP模型可采用后向值迭代算法(Value Iteration)进行求解。在有限的状态空间和有限的决策范围前提下，值迭代算法可获得最优控制策略的数值解[24]。但当状态空间较大时，维度诅咒使得这两个模型几乎无法求解。因此，本文首先在数值实验中观察最优控制策略数值解的特征，然后进一步提出参数化近似启发式控制策略，并通过遗传算法与离散事件仿真对近似启发式控制策略的参数进行优化，最后通过仿真实验与敏感度分析验证本文所提近似启发式控制策略的性能。本文数值实验均在Intel酷睿i5-6300HQ CPU，2.30GHz，8GB内存的环境下运行。

3.1 参数设置

考虑到患者输血效用以及积压、失销和过期惩罚成本不易直接量化，本文参考了相关文献的参数设置来进行数值实验。目前血小板库存文献中考虑输血效用的文献相对较少，且多数文献将血小板库存系统考虑为单纯的失销系统，本文模型中需要用到的不同新鲜度血小板的输血效用以及失销、积压和过期惩罚成本参数难以从单一的文献中获得参考。本文的参数设置主要参考了表1的三篇文献，其中考虑输血效用的两篇文献Tetteh[19]和Slofstra[20]均未设置Basecase，Tetteh[19]设置了一个因素水平表进行了仿真实验, Slofstra[20]通过设置一系列不同的短缺成本和浪费成本交叉进行仿真实验(单位输血效用惩罚不变)。为了避免单一参数设置对实验结果的影响，本文分别针对普通需求和紧急需求设计了四因素四水平的表格来验证实验结果，参数设置见表2和表3。

表1 参数设置参考文献

表2 普通需求参数设置因素水平表

表3 紧急需求参数设置因素水平表

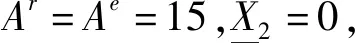
3.2 最优控制策略

3.2.1 最优订货策略

以cs=100,cw=80,r1=400,r2=500为例，对普通需求下的马尔可夫决策模型通过值迭代算法进行求解，得到最优订货量qt随x1t和x2t的变化规律如图1所示，其中x2t为第t天初的新鲜库存量，x1t≥0时为第t天初的陈旧库存量，x1t<0时为第t天初积压的普通需求量。观察图1发现普通需求下最优订货策略近似为带有订货下限的阈值订货策略，其主要特征如下：

特征1随着x1t和x2t的增加，最优订货量是非增的，且最多减1。

特征2最优订货量qt与总库存水平(x1t+x2t)近似有一个阈值关系，多数情况下会将总库存水平补货至一个确定的阈值。观察图1可发现-12≤x1t+x2t≤2时最优订货策略均将总库存水平订货至一个固定的阈值6，其他情况下阈值稍有变化，如x1t+x2t=3,4,5时阈值变为7。

特征3最优订货策略对于不同的新鲜库存状态x2t有不同的订货量下限。总库存(x1t+x2t)一定，新鲜库存x2t较小时需要稍大的订货量下限，因为这种情况下陈旧库存相对较多，由于陈旧库存当天结束时会由于过期而离开系统，无法应对未来需求，因此需要稍大的订货量下限以在第二天及时补充新鲜库存。总库存一定，随着新鲜库存x2t的增多，陈旧库存减少，订货量下限逐渐降低。

图1 普通需求下的最优订货策略(以cs=100,cw=80,r1=400,r2=500为例)

分别以cs=100,cl=400,r1=400,r2=500和cs=50,cl=400,r1=450,r2=450为例，在紧急需求下对模型通过后向值迭代算法进行求解，得到最优订货量qt随x1t和x2t的变化规律如图2和图3所示，其中x1t为第t天初的陈旧库存量，x2t为第t天初的新鲜库存量。观察图2和图3发现紧急需求下的最优订货量qt主要随着新鲜库存状态x2t变化，少数情况下受总库存水平(x1t+x2t)的影响有近似的阈值结构，但是阈值相对不稳定。紧急需求下最优订货策略的主要特征同样满足上述普通需求下最优订货策略的三条特征，不同的是紧急需求下特征2的订货阈值相对不稳定，反而特征3随新鲜库存状态x2t变化的订货下限起了主要作用。这是因为紧急需求模型中需求未满足成本相对较高，应对未来需求不确定性的新鲜库存x2t对系统性能的贡献更加突出，强化了特征3。

图2 紧急需求下的最优订货策略(以cs=100,cl=400,r1=400,r2=500为例)

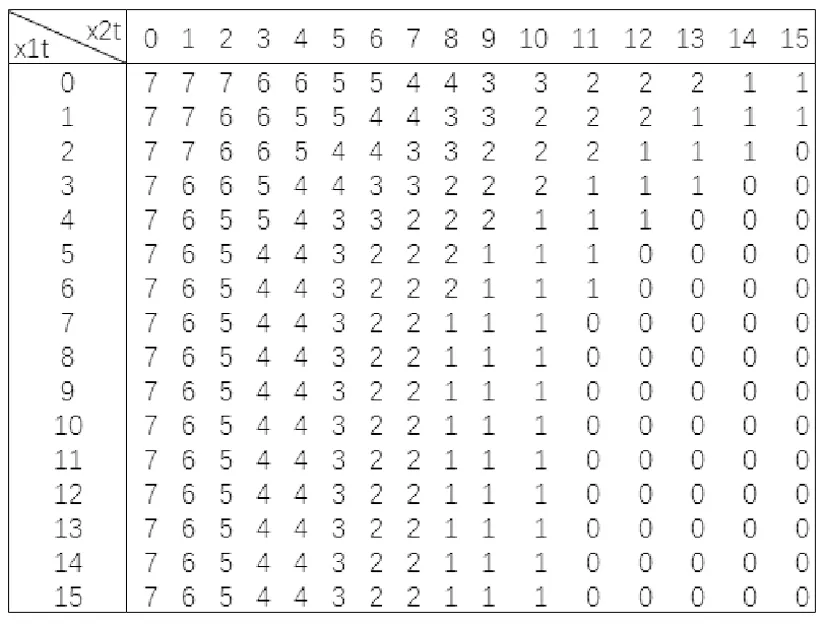
图3 紧急需求下的最优订货策略(以cs=50,cl=400,r1=450,r2=450为例)

3.2.2 最优使用策略

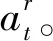
(1)若(-x1t)++at≤x2t-q2t，有y2t=(-x1t)++at。总需求(-x1t)++at小于新鲜血小板库存x2t与额度q2t之差时，需求全部用新鲜库存来满足。

(2)若x2t-q2t<(-x1t)++at≤x2t-q2t+(x1t)+，有y2t=x2t-q2t。总需求(-x1t)++at大于新鲜血小板库存x2t与额度q2t之差但小于新鲜血小板库存x2t与额度q2t之差加陈旧血小板库存(x1t)+时，先将新鲜血小板库存x2t使用至额度q2t，然后剩下的需求用陈旧血小板库存(x1t)+满足。

(3)若x2t-q2t+(x1t)+<(-x1t)++at，有y2t=min((-x1t)++at-(x1t)+,x2t)。总需求(-x1t)++at大于新鲜血小板库存x2t与q2t额度之差加陈旧血小板库存(x1t)+时，先使用陈旧血小板库存(x1t)+，剩下的需求用新鲜血小板库存x2t满足。

3.3 启发式策略

(1)本文通过观察3.2节值迭代算法求出的最优控制策略数值解的主要特征，构造近似最优的参数化启发式控制策略如下：①近似订货策略为带有订货下限的阈值订货策略。进行订货决策时首先将总库存水平订货至一个固定的订货阈值TH，根据新鲜库存x2t的不同状态确定不同的订货下限，如果基于阈值的订货量小于x2t对应的订货量下限则按照该订货量下限进行订货。②近似使用策略为配额策略(Quota Policy)。假设有一个不随状态变化的配额q2，使用前先保留额度为q2的新鲜库存，然后对剩余库存采用LIFO的规则进行使用，如果剩余库存无法满足当期需求，最后再使用q2部分的新鲜库存。

(2)为了对比不同订货策略对系统性能的影响，简化近似策略的订货下限结构得到阈值订货策略+Quota使用策略：①进行订货决策时将总库存水平(x1t+x2t)订货至一个固定的订货阈值TH。②使用策略采用配额策略，假设有一个不随状态变化的配额q2。

(3)为了验证本文的近似策略相对于传统策略的优越性，本文以Haijema等[12]中优化得到的阈值+FIFO策略进行对比。该作者根据医院实际使用情况假设血小板使用策略为FIFO策略，并通过SDP方法平衡短缺和浪费来优化订货策略，优化后近似为阈值策略。阈值订货策略+FIFO使用策略(传统优化策略)具体如下：①进行订货决策时将总库存水平(x1t+x2t)订货至一个固定的订货阈值TH。②使用策略采用FIFO使用策略。

3.4 仿真实验

根据3.1节中因素水平表的参数设置进行仿真实验，分别在普通需求和紧急需求下对最优控制策略以及不同的启发式策略进行仿真，以状态(0,0)为初始状态，运行100000天并输出日均效用，其中近似策略的参数通过精英保留遗传算法进行仿真优化，阈值+Quota以及阈值+FIFO策略的阈值通过枚举法进行仿真优化。

遗传算法的收敛性：对于近似启发式策略，遗传算法的参数设置如下：群体规模50，交叉概率0.7，变异概率0.04，最大进化代数1000。以普通需求下cs=100,cw=80,r1=400,r2=500为例，近似策略的运行时间为425s，算法所得最好值见图4。从图4可以看出遗传算法在约200代时达到收敛，收敛速度较快。改变参数组合，收敛情况发生变化，但是基本在300代之前可达到收敛，少数参数组合在500代之前可达到收敛。

图4 普通需求下近似策略遗传1000代最优值收敛曲线(以cs=100,cw=80,r1=400,r2=500为例)

紧急需求和普通需求下所有参数组合在启发式策略下的仿真结果与最优策略的Gap分别见表4和表5。观察发现紧急需求下近似策略与最优策略的平均Gap仅有0.19%，在绝大多数情况下均可很好的近似最优策略；阈值+Quota策略与最优策略的平均Gap为2.97%，在部分参数组合下表现较好，但是其表现并不稳定，与最优策略的最大Gap可达7.53%；阈值+FIFO策略表现最差，与最优策略的最大Gap可达20.22%。普通需求下近似策略与最优策略的平均Gap仅有0.06%，在所有参数组合下均可很好的近似最优策略；阈值+Quota策略与最优策略的平均Gap为0.68%，在大部分参数组合下表现良好，但是其表现并不稳定；阈值+FIFO策略表现最差，与最优策略的最大Gap可达11.52%。

表4 紧急需求下不同启发式策略与最优策略日均效用Gap对比

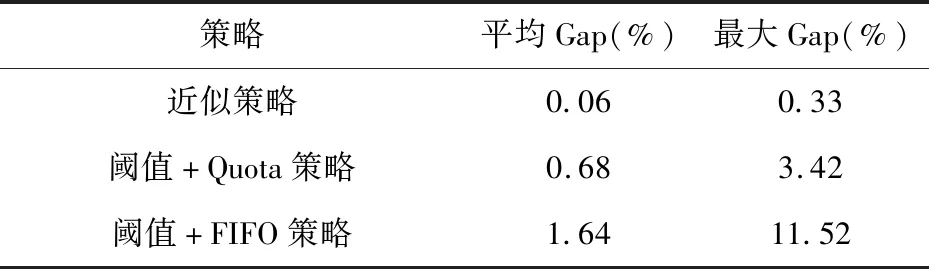
表5 普通需求下不同启发式策略与最优策略日均效用Gap对比

图5至图12分别绘制了两种需求不同因素水平下三种启发式策略与最优策略的平均Gap对比，观察发现：

1)观察图5和图6发现随着单位浪费成本cs的增加，近似策略与最优策略的Gap一直处于一个较低的水平，阈值+Quota策略和阈值+FIFO策略与最优策略的Gap均下降。随着单位浪费成本的增加，阈值+FIFO策略逐渐接近阈值+Quota策略，说明单位浪费成本越高，为了避免产生浪费，满足需求时越趋向于先使用陈旧库存，最优使用策略越趋向于FIFO策略。对比近似策略和阈值+Quota策略，发现带有订货下限的阈值订货策略明显优于简单的阈值策略。

2)观察图7和图8发现随着单位失销成本cl和单位积压成本cw的增加，近似策略与最优策略的Gap一直处于一个较低的水平。紧急需求下随着单位失销成本cl的增加，阈值+Quota策略与最优策略的Gap无明显变化，阈值+FIFO策略与最优策略的Gap稍增；普通需求下随着单位积压成本cw的增加，阈值+Quota策略和阈值+FIFO策略与最优策略的Gap均增加。这说明单位短缺成本越高，带有订货下限的阈值订货策略相对于简单的阈值订货策略的优势越明显。

3)观察图9至图12发现随着新鲜血小板单位输血效用r2以及不同新鲜度血小板单位输血效用比r1/r2的增大，近似策略与最优策略的Gap一直处于一个较低的水平。随着r2的增加，阈值+Quota和阈值+FIFO策略与最优策略的Gap均无明显变化；随着r1/r2的增大，不同新鲜度血小板之间的单位输血效用差减小，阈值+Quota和阈值+FIFO策略与最优策略的Gap均明显减小。这说明不同新鲜度血小板之间的单位输血效用差别越大，近似策略相对于阈值+FIFO策略的优越性越明显。随着不同新鲜度血小板之间的单位输血效用差的减小，最优使用策略逐渐趋向于FIFO使用策略，阈值+Quota策略和阈值+FIFO策略的Gap逐渐减小。即使不考虑不同新鲜度血小板之间的单位输血效用差别，带有订货下限的阈值订货策略也明显优于简单的阈值策略。

图5 不同单位浪费成本下三种启发式策略与最优策略的平均Gap对比(紧急需求)

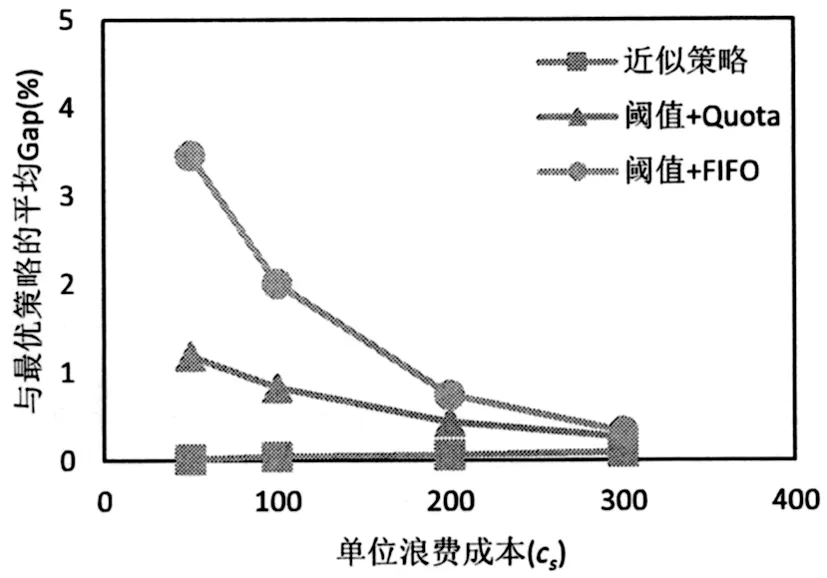
图6 不同单位浪费成本下三种启发式策略与最优策略的平均Gap对比(普通需求)

图7 不同单位失销成本下三种启发式策略与最优策略的平均Gap对比(紧急需求)

图8 不同单位积压成本下三种启发式策略与最优策略的平均Gap对比(普通需求)

图9 不同新鲜血小板单位输血效用下三种启发式策略与最优策略的平均Gap对比(紧急需求)

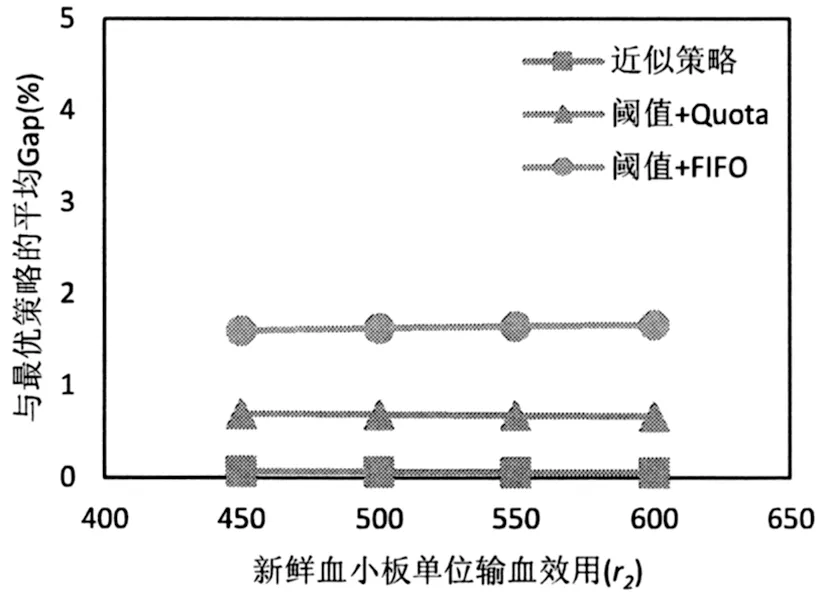
图10 不同新鲜血小板单位输血效用下三种启发式策略与最优策略的平均Gap对比(普通需求)

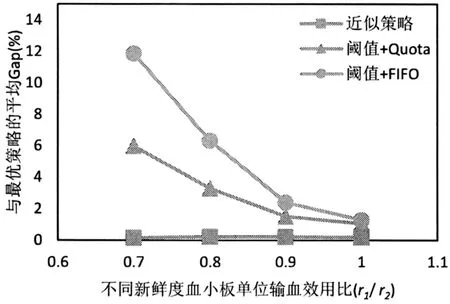
图11 不同新鲜度血小板单位输血效用比下三种启发式策略与最优策略的平均Gap对比(紧急需求)

图12 不同新鲜度血小板单位输血效用比下三种启发式策略与最优策略的平均Gap对比(普通需求)

图13和图14分别绘制了两种需求不同需求到达率下三种启发式策略与最优策略的Gap对比，观察发现随着需求到达率的增加，近似策略与最优策略的Gap一直处于一个较低的水平，阈值+Quota策略与最优策略的Gap下降，阈值+FIFO策略在两种需求模式下均表现最差。这说明近似策略可以很好的适应不同的需求到达率，而阈值+Quota策略在需求到达率较高的情况下也是一种相对较好的策略。

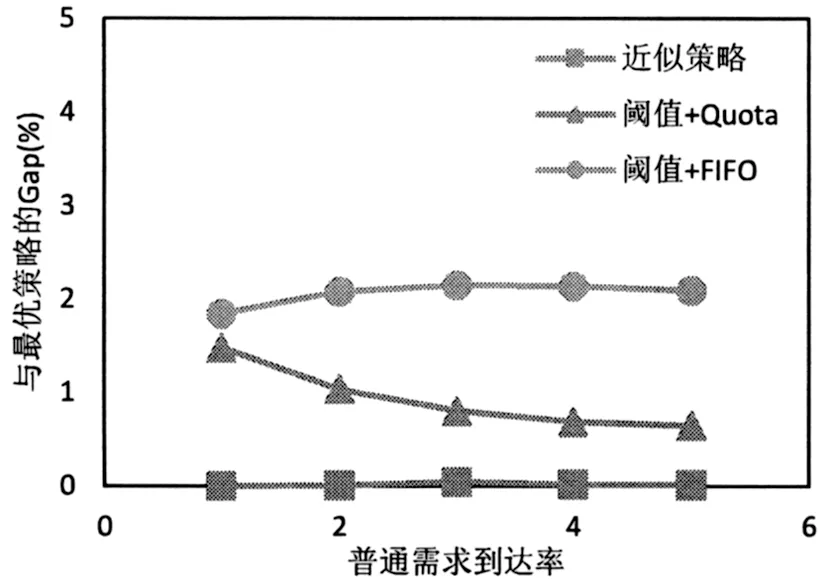
图11 不同普通需求到达率下三种启发式策略与最优策略的Gap对比(以cs=100,cw=80,r1=400,r2=500为例)

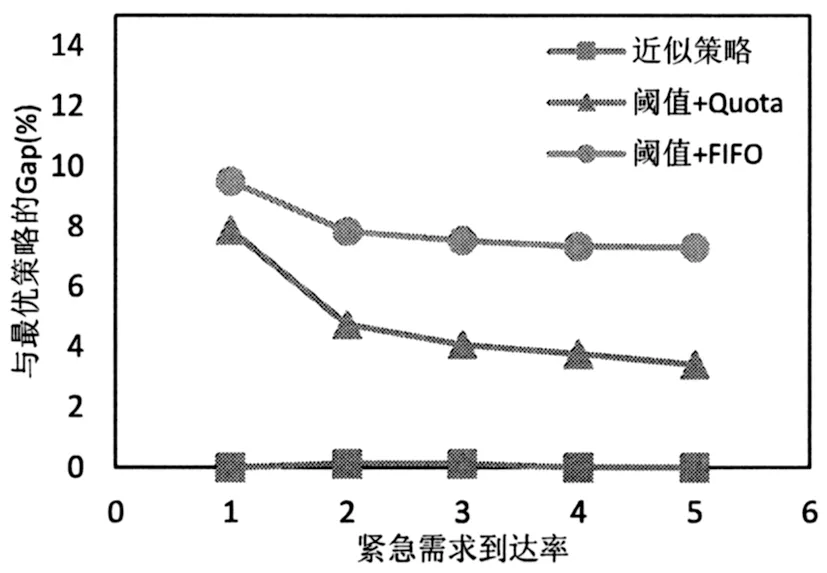
图14 不同紧急需求到达率下三种启发式策略与最优策略的Gap对比(以cs=100,cl=400,r1=400,r2=500为例)

4 结论

为了更合理的利用稀缺血液资源，本文研究了血小板库存控制的订货和使用策略的联合优化问题。以最小化短缺和浪费并最大化输血效用为目标，提出了有限时域的MDP模型进行动态决策。系统每天天初根据分年龄库存状态进行订货决策，之后随着不同需求的到达，医院需要及时根据分年龄库存状态以及需求情况进行使用决策。对MDP模型的最优控制策略进行求解，发现最优订货策略可近似为带有订货下限的阈值策略，最优使用策略为配额策略。为了便于实施，本文通过观察最优控制策略数值解的主要特征提出了参数化启发式控制策略，通过遗传算法对启发式控制策略的参数进行优化，并通过数值实验进行验证，发现紧急需求和普通需求下带有订货下限的阈值订货策略明显优于简单的阈值策略，配额策略明显优于FIFO使用策略。

未来的研究可结合需求到达情况考虑不同需求的混合及相互影响，将血小板的有效寿命扩展至三天并考虑不确定性供给，使得模型更加贴合实际。此外，本文模型忽略的血小板血型问题可能会对订货策略产生一定影响，比如相容性高的血小板如O型血可适当多订。未来可考虑血型以及异型输注惩罚。