考虑决策者心理行为的直觉语言多属性决策方法

刘宁元

(广东轻工职业技术学院 财贸学院，广东 广州 510000)

0 引言

自从Zadeh[1]提出模糊集以来，关于模糊集在决策理论中的研究已经引起了人们广泛关注。由于客观事物的不确定性和复杂性，有些决策问题的评价信息难以用模糊数值量化，而倾向应用语言评价集[2]来表达，例如公司绩效、管理能力、个人潜力等。近年来，关于语言多属性决策问题研究已经成为决策分析中的热点[3,4]。然而语言评价集隐含了决策者对该语言评价集的信任程度为1，没有反映决策者对语言评价集的不信任程度和犹豫不决的程度。Atanassov[5]在模糊集隶属度的基础上增添了非隶属度，提出了直觉模糊集概念，它能更细腻地反映模糊信息。王坚强等[6]对直觉模糊集进行了拓展，在语言评价集的基础上增加了直觉模糊集的隶属度和非隶属度，定义了直觉语言集概念。利用语言评价集以及论域中元素对该语言评价集的隶属度、非隶属度来表示的直觉语言集，在实际决策问题中反映语言评价集决策信息的不确定性与模糊性更适合和准确。因此，针对直觉语言信息多属性决策问题的研究具有重要意义。王坚强等[6,7]定义了直觉语言加权算子、直觉语言加权几何平均算子，给出了新的直觉模糊熵的计算方法，提出了一种基于直觉模糊熵的直觉语言多属性决策方法。Liu[8]首先定义了直觉语言广义混合加权算子(ILGDHWA)、直觉语言广义有序加权平均算子(ILGDOWA)，并讨论了这些算子的性质，提出了一种基于ILGDHWA算子和ILGDOWA算子的多属性群决策方法。Wang等[9]定义了新的直觉语言数得分函数和精确函数，提出了直觉语言有序加权几何算子(ILOWG)、直觉语言混合几何算子(ILHG)，给出了一种基于ILOWG算子和ILHG算子的多属性群决策方法。

需要指出的是，针对直觉语言多属性的决策问题，通常是基于期望效用理论对决策问题进行分析研究。该理论有一个前提假设，认为决策者在决策过程中具有“完全理性”的心理行为特征，然而决策者在实际决策过程中往往很难做到绝对理性，通常具有“有限理性”的心理行为特征[10]。Kahneman和Tversky在考虑行为决策理论的基础上提出了前景理论[11]，其在多属性决策问题的研究中得到了广泛应用[12,13]。Gomes和Lima[14]提出一种建立在前景理论基础上的交互式多属性决策方法―TODIM(Tomada de decisao interativa e multicritevio)方法。与前景理论区别在于，TODIM方法将备选方案的评价属性值作为决策参考点信息,通过在每个属性下对两两备选方案进行比较来计算收益-损失值优先度，从而解决多属性决策问题，具有涉及较少参数、计算过程简便等优点。此后，关于TODIM决策方法在多属性决策问题上的应用引起了国内外学者广泛关注。樊治平等[15]提出了一种属性值为区间数的TODIM决策方法。该方法基于方案评价值的距离来构建方案的益损值优先度矩阵,进而通过计算备选方案的综合优先度进行方案排序择优。Souza和Krohling等[16]提出了一种属性值为梯形模糊数的TODIM决策方法。Zhang等[17]分别定义了犹豫模糊数和区间犹豫模糊数新的测度函数和距离测度，提出了一种属性值为犹豫模糊数和区间犹豫模糊数混合的TODIM决策方法。梁霞等[18]考虑了属性值具有关联的多属性决策问题，提出了一种新的C-TODIM决策方法。姜艳萍等[19]提出一种属性信息不完全的TODIM决策方法，该方法通过在每个属性下计算方案间的优先度，建立以所有方案优先度最大化为目标函数的最优方案优化模型，从而对方案进行排序。孔令艳等[20]给出了犹豫模糊语言排序的可能度公式，提出了属性值为犹豫模糊语言的TODIM决策方法。继前景理论之后，Loomes等[22]、Bell[21]分别独立提出了另一种典型的行为决策理论—后悔理论，并取得了一些研究成果[23～25]。

以上关于TODIM决策方法的研究，不仅扩大了TODIM方法应用范围，还是对行为决策理论与方法研究成果的进一步丰富和完善。由于在实际多属性决策中，基于语言信息决策理论研究中应用直觉语言评价值来表达信息的决策问题普遍存在，然而目前关于属性值是直觉语言信息的多属性决策问题研究还处于起步阶段，为此本文针对直觉语言信息的决策问题应用TODIM方法进行了研究，提出一种考虑决策者心理行为的直觉语言多属性决策方法。

1 直觉语言数及其相关定义

为了简便,文献[6]称三元组a=为直觉语言数。例如,当l=4时,定义语言评价集S={s0=极差，s1=很差,s2=差，s3=略差，s4=一般，s5=略好，s6=好，s7=很好，s8=极好}。直觉语言数a=表示评估者认为评估元素是s4“一般”的确定值为0.7,不是s4“一般”的确定值为0.1(即否定是s4“一般”值为0.1)，是否是s4“一般”的犹豫不决,不能确定值为0.2。

定义2[6]设直觉语言数a=,则a的期望值为:

E(a)=sθ(a)×[μ(a)+1-v(a)]/2

(1)

定义3[6]设直觉语言数a=,则a的得分函数S(a)和精确函数H(a)分别为:

S(a)=I(E(a))×(μ(a)-v(a))

(2)

H(a)=I(E(a))×(μ(a)+v(a))

(3)

其中,I(sθ)=θ为取下标函数,E(a)表示a的期望值。

定义4[6]设任意两个直觉语言数a1=、a2=,则

(1)若S(a1)>S(a2),则a1>a2；

(2)若S(a1)=S(a2),且H(a1)=H(a2),则a1=a2；

(3)若S(a1)=S(a2),且H(a1)>H(a2),则a1>a2。

定义5[24]设任意两个直觉语言数a1=、a2=、则a1和a2间的Hamming距离为

d(a1,a2)=|θ(a1)μ(a1)-θ(a2)μ(a2)|+

|θ(a1)(1-v(a1))-θ(a2)(1-v(a2))|

(4)

2 问题描述

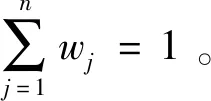
3 决策方法

3.1 方法思路

在考虑决策者参照依赖和损失规避心理行为的基础上，针对上述决策问题，提出一种决策分析方法。

(5)

其中，Nb、Nc分别为效益型属性与成本型属性的下标集合，满足Nb∪Nc=N,Nb∩Nc=Ø。

将各属性下方案的收益-损失值变换到同一维度上[26],计算属性wj相对于参照属性wr的相对权重为wjr, 即

(6)

其中，wr=max1≤j≤n(wj)。

进一步在每个属性Aj下，通过比较每个方案Xi相对于其它方案Xk的得分函数，来计算方案的收益-损失值优先度φj(Xi,Xk),并构造收益-损失值优先度矩阵Φj=[φj(Xi,Xk)]m×m。其中φj(Xi,Xk)计算公式为：

(7)

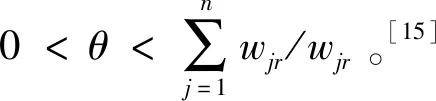
(8)

这反映在决策过程中，当面对同等大小的收益值或损失值时，决策者在对待损失时会更加敏感。

进一步地，将所有属性Aj(j∈N)下方案Xi相比较其它所有方案Xk的收益-损失值优先度φj(Xi,Xk)进行集结，得到方案优先度值φ(Xi,Xk)，构建方案优先度矩阵Φ=[φ(Xi,Xk)]m×m,其计算公式为:

(9)

进而，利用式(10)计算备选方案Xi(i=1,2,…,m)综合优先度T(Xi)

(10)

最后,将综合优先度T(Xi)规范化为ϑ(Xi),其计算式为:

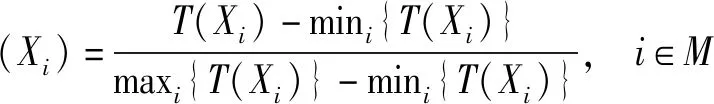
(11)

显然，0≤ϑ(Xi)≤1且ϑ(Xi)越大，方案Xi越好。因此,依据ϑ(Xi)值的大小对方案进行排序。

3.2 决策步骤

综上，基于直觉语言TODIM多属性决策方法具体步骤如下：

步骤3利用式(4)、式(6)和式(7)在每个属性Aj下通过比较每个方案Xi相对于其它方案Xk的得分函数，计算方案收益-损失值优先度φj(Xi,Xk),并构造收益-损失值优先度矩阵，Φj=[φj(Xi,Xk)]m×m(i,k∈M,j∈N)。

步骤4利用式(9)集成方案Xi(i∈M)在所有属性下相比较于其它所有方案Xk的收益-损失值优先度φj(Xi,Xk)，得到方案优先度值φ(Xi,Xk),构建方案优先度矩阵Φ=[φ(Xi,Xk)]m×m(i,k∈M)。

步骤5利用式(10)求出每个备选方案综合优先度T(Xi)(i∈M)。

步骤6利用式(11)求出ϑ(Xi)(i∈M)并依据其值大小对备选方案进行排序择优。

4 算例分析

4.1 算例

以文献[6]为例，一个多属性决策问题，有5个方案X={X1,X2,…,X5}，5个属性A={A1,A2,…,An}属性都是效益型，权重向量w=(0.20,0.15,0.25,0.10,0.30)。假设决策者通过比较分析后,应用语言短语集S(l=4)对5个方案进行评价，得到方案Xi在属性Aj下的属性值用直觉语言数bij=(i=1,2,…,5;j=1,2,…,5)表示,决策矩阵B=[bij]5×5如表1所示。试确定这5个方案的排序。

表1 方案的评估值B=[bij]5×5

表2 在Aj(j=1,2,3,4,5)属性下方案的收益-损失比较分析

步骤3利用式(4)、式(6)和式(7)计算在各属性Aj(j=1,2,…,5)下方案的收益-损失值优先度φj(Xi,Xk)取(θ=1)，并构造收益-损失值优先度矩阵φj=[φ(Xi,Xk)]5×5(i,k=1,2,…,5;j=1,2,…,5)如表3所示。

步骤4利用式(9)集成方案Xi(i=1,2,…,5)在所有属性下相比较于其它所有方案Xk的收益-损失值优先度φj(Xi,Xk),得到方案优先度值φ(Xi,Xk),构建方案优先度矩阵Φ=[φ(Xi,Xk)]5×5，如表3所示。

表3 方案优先度短阵Φ=[φ(Xi,Xk)]5×5

步骤5利用式(10)求出每个备选方案综合优先度T(Xi):

T(X1)=-54.8429,T(X2)=-16.3691
T(X3)=-18.5056,T(X4)=-54.2458
T(X5)=-12.1043

步骤6利用式(11)求出ϑ(Xi)：

ϑ(X1)=0.0000, ϑ(X2)=0.9002
ϑ(X3)=0.8502, ϑ(X4)=0.0140
ϑ(X5)=1.0000

最后,依据ϑ(Xi)的大小,得到方案的排序结果为：X5≻X2≻X3≻X4≻X1。

4.2 比较分析

下面用两种不同的决策方法与本文方法进行比较。这两种决策方法为不同情况：1)没有考虑决策者有限理性的心理行为特征,使用文献[6]中方法对本文算例进行求解；2)考虑决策者有限理性心理行为特征，使用文献[12]中方法对本文算例进行求解。将两种决策方法得到的结果与本文方法进行比较,如表4所示。

表4 不同决策方法的排序

当没有考虑决策者“有限理性”的心理特征时，采用文献[6]决策方法对决策矩阵的属性评价信息运用直觉语言加权算术平均算子进行集成，得到备选方案的总体属性值，最后根据总体属性值的得分函数和精确函数的大小对备选方案进行排序。虽然本文与文献[6]最优方案都是X5,但在方案X1、X4的排序有所不同。文献[6]的决策方法建立在假设决策者具有“完全理性”心理行为特征的基础之上，然而在实际过程中，决策者的决策行为很难做到“完全理性”。与文献[6]相比，本文决策方法更加符合实际情况。

当考虑决策者“有限理性”的心理特征时,使用文献[12]基于累积前景理论的决策方法,首先定义新的直觉语言数距离,利用本文的属性权重w=(0.20,0.15,0.25,0.10,0.30),在参数上取值α=0.89,β=0.92,θ=2.25[12],计算备选方案的综合累积前景值,并对方案进行排序。本文与文献[12]中的方法都考虑了决策者参照依赖和损失规避的心理行为特征，虽然与文献[12]排序结果是一致,但与文献[12]中的决策方法相比，本文方法在计算过程中涉及较少参数、计算相对简便,具有一定的优势。

4.3 参数敏感分析

考虑决策者心理行为的直觉语言多属性决策方法是带有参数θ(损失衰减系数)的决策方法。该参数θ(损失衰减系数)敏感分析是针对各属性下方案优先度φ(Xi,Xk)计算过程中，会因为参数θ的不同取值而发生变化，从而引起方案综合优先度发生改变，最终影响备选方案的排序。下面改变参数θ的取值θ=0.1、θ=0.5、θ=1，观察备选方案排序情况。见表5所示。

表5 参数θ取值不同的方案排序

从表5中的敏感性分析结果看出,随参数θ值变化,方案的排序有所改变,但备选方案中最优者都是X4。这说明损失衰减系数θ的不同取值对方案的最终排序有影响。

5 结束

本文针对语言多属性决策中应用直觉语言集来表达决策信息的决策问题，在考虑决策者有限理性的心理行为基础上，提出一种决策方法。该方法通过在每个属性下每个方案相比较于其它方案的得分函数,构建方案间收益-损失值优先度矩阵，在考虑决策者参照依赖和损失规避心理行为的基础上，计算备选方案的综合优先度,并根据其大小对方案进行排序择优。该方法具有步骤清晰、计算相对简便，为直觉语言多属性决策问题的解决提出了一条新的有效途径。