基于赫兹接触的钢轨砂带打磨温度建模研究

王文玺， 李建勇， 樊文刚， 聂 蒙

(1. 北京交通大学 机械与电子控制工程学院， 北京 100044；2. 北京交通大学 载运工具先进制造与测控技术教育部重点实验室， 北京 100044)

自我国高速铁路提速以来，面临营运里程快速增长与“天窗时间”骤减对轨道线路打磨养护作业所带来的更加迫切的需求和更为严峻的挑战[1-3]。当前，主流的线路打磨技术以砂轮式端面打磨为主，辅之以钢轨铣磨。然而，因砂轮属于刚性打磨工具，自身存在易破碎、易磨损和易造成二次损害的问题，限制了砂轮式钢轨打磨技术的运用和发展。相对地,砂带打磨技术具有弹性磨削、高效磨削、冷态磨削、拆卸方便和动力简化等优势，使其具有了发展为新型钢轨打磨技术的可能性，成为应对钢轨打磨作业需求高效化、智能化和多样化的有效途径[4-5]。

钢轨砂带打磨属于强力磨削范畴，作业过程会有大量磨削功转化为热量进入打磨区。热量堆积使钢轨温度不断升高，而过高的温度会导致钢轨表层金相组织变化甚至发蓝、灼烧，造成打磨事故。因此，建立钢轨砂带打磨作业过程温度模型对于优化打磨工艺参数、控制磨削温升具有重要意义。聂蒙等[6]从瞬时点热源温度场出发，建立了钢轨砂轮打磨移动线接触温度场数学模型，分析了打磨速度、砂轮尺寸及磨头数量对打磨温度的影响，并最终给出了打磨功率与作业速度配比曲线。张青等[7]基于热力耦合方法，建立了钢轨打磨有限元模型，发现温度场、应力场均成椭圆状，且打磨过程是快速升温、缓慢降温过程。

本文针对实际工况中弹性曲面接触特点，基于磨削温度理论建立钢轨砂带打磨温度模型，并通过数值仿真分析工艺参数对打磨温度的影响。

1 钢轨砂带打磨作业原理

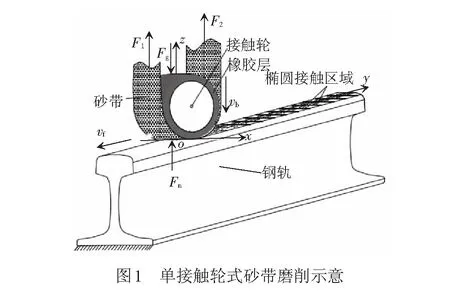
图1介绍了平型接触轮式的钢轨砂带打磨作业过程。砂带打磨机构磨头包含接触轮及外围砂带，接触轮由刚性轮毂和外包弹性橡胶构成,通过加压气缸所施载荷Fg将接触轮和砂带一并压向钢轨轨面。砂带在张紧力F1、F2的牵引作用下，以线速度vb高速回转执行打磨。磨头随打磨列车以速度vf沿轨向进给。对于GB60轨而言，轨面廓形沿x方向由三种不同曲率圆弧组成，而在y方向受波磨影响也存在一定曲率。所以，此时的接触状态可看作两曲面间的弹性接触。根据赫兹接触理论，该接触区域呈椭圆形，其上压力分布呈半椭球状[8-9]，见图2。

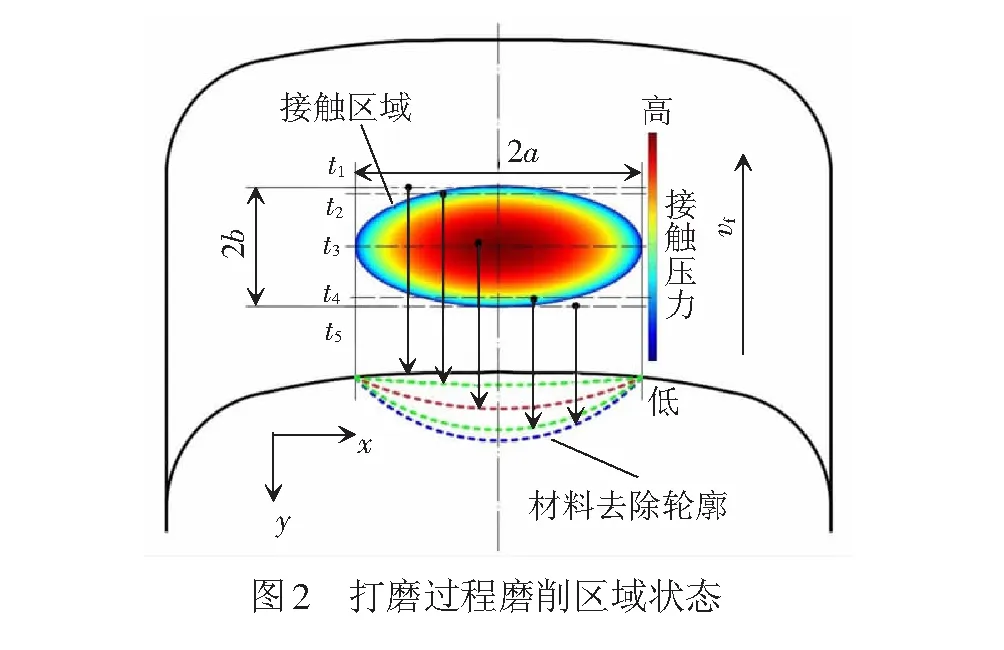
2 接触区域外形与压力分布

以接触轮轴方向为x方向，轨向为y方向，轨顶法矢方向为z方向建立全局直角坐标系，见图3。以与x轴平行方向为w方向，与y轴平行方向为l方向，与z轴平行方向为v方向，建立如图所示接触区域局部坐标系。根据赫兹接触理论，接触轮与钢轨表面压力分布pn为

( 1 )

式中：a、b分别为椭圆接触区域的长、短半轴长

( 2 )

( 3 )

其中，ma、mb分别为与椭圆离心率相关的中间变量；Σd为接触轮与钢轨主曲率和；υ1、υ2分别为橡胶和钢轨泊松比；E1、E2分别为接触轮和钢轨弹性模量。

ma、mb、∑d和E1计算为

( 4 )

( 5 )

∑d=d11+d12+d21+d22

( 6 )

( 7 )

式中：eofc为椭圆离心率；L(eofc)为第二类椭圆积分；d11、d12为接触轮主曲率；d21、d22为钢轨主曲率；E12、E12分别为接触轮毂和橡胶层弹性模量；e11、e12分别为轮毂和橡胶层厚度。k、eofc、L(eofc)和E12计算为

E12=10e0.019 8Hs-0.543 2

( 8 )

( 9 )

(10)

(11)

其中，Hs为橡胶邵氏硬度。

在一般接触问题中，主曲率函数F(d)定义为

(12)

式中：ω为两接触部件主平面间夹角。根据Wang等[9]关于自由曲面砂带磨削材料去除模型的研究结果，F(d)还可由离心率e表达为

(13)

式中：K(e)为第一类椭圆积分，可计算为

(14)

最后，联立式(12)与式(13)通过数值方法可求得椭圆接触区域短长轴比k，进而实现整个Herz接触边界及接触应力的求解。

3 打磨过程温度模型

根据库仑摩擦定律，设接触区域各切向力正比与法向力，则接触区域切向力分布pt为

(15)

式中：μ为摩擦系数。

则接触面的做功分布qg为

(16)

考虑到表面热流情况，则接触表面热源分布情况qs为

qs(l,w)=

(17)

式中：Kw、Kg分别为工件和磨粒的导热系数。

3.1 单接触轮打磨作业温度模型

钢轨砂带打磨依靠磨头机构上单个或多个外包砂带接触轮在打磨小车牵引下沿列车行进方向对钢轨进行修磨。打磨过程中通过控制打磨电机功率改变打磨量。因每个磨粒与钢轨表面作用时间极短，可将单颗磨粒热效应等效为瞬时点热源温度场，瞬时点热源温度场模型为[10]

(18)

式中：Tp为瞬时点热源温度；(x,y,z)为温度场考量点坐标；(x0,y0,z0)为点热源坐标；Qp为热源总热量；tg为作用时间；c为材料比热容；ρ为工件材料密度；α为工件材料热扩散率。

持续沿直线方向进给点热源所形成的温度场可视作在总作用时间tg内任意时刻t对某一点M(x,y,z)所形成热效应的累加过程。所以在某一时刻t的dt时间内，点热源形成的温度场为

dTpm=

(19)

式中：qp为点热源的发热功率；t为总作用时间tg内某一时刻；vf为打磨小车行驶速度。

因此整个作用时间内点热源温度场为

Tpm=θpm(x,y,z,tg)=

(20)

将接触区域沿l方向分解为dw宽的无数条接触线，见图3。取任意w处一条接触线进行分析，则l处的微元dl形成的移动温度场为

(21)

式中：qs为单位面积发热强度，由上节分析可知是关于(l,w)的函数；(xs,ys)为接触线起始点与坐标原点的相对位置。xs、ys分别为

(22)

则整个接触线温度场为

(23)

整个移动椭圆接触区域叠加形成的温度场为

(24)

3.2 多接触轮打磨作业温度模型

多个接触轮同时作业所形成的复合温度场可以通过对各单个接触轮温度场进行叠加得到。各自形成的温度场为

(25)

式中：ai、bi分别为第i个接触轮对应接触区域长、短半轴；qi为第i个接触轮的单位面积产热率；(xi,yi,zi)为第i个接触轮相对于原点的坐标。进而复数接触轮所形成的温度场为

4 模型数值仿真与分析

通过Matlab对解析模型进行数值仿真。仿真过程中忽略环境温度，仿真参数根据实际打磨作业情况选取，见表1。

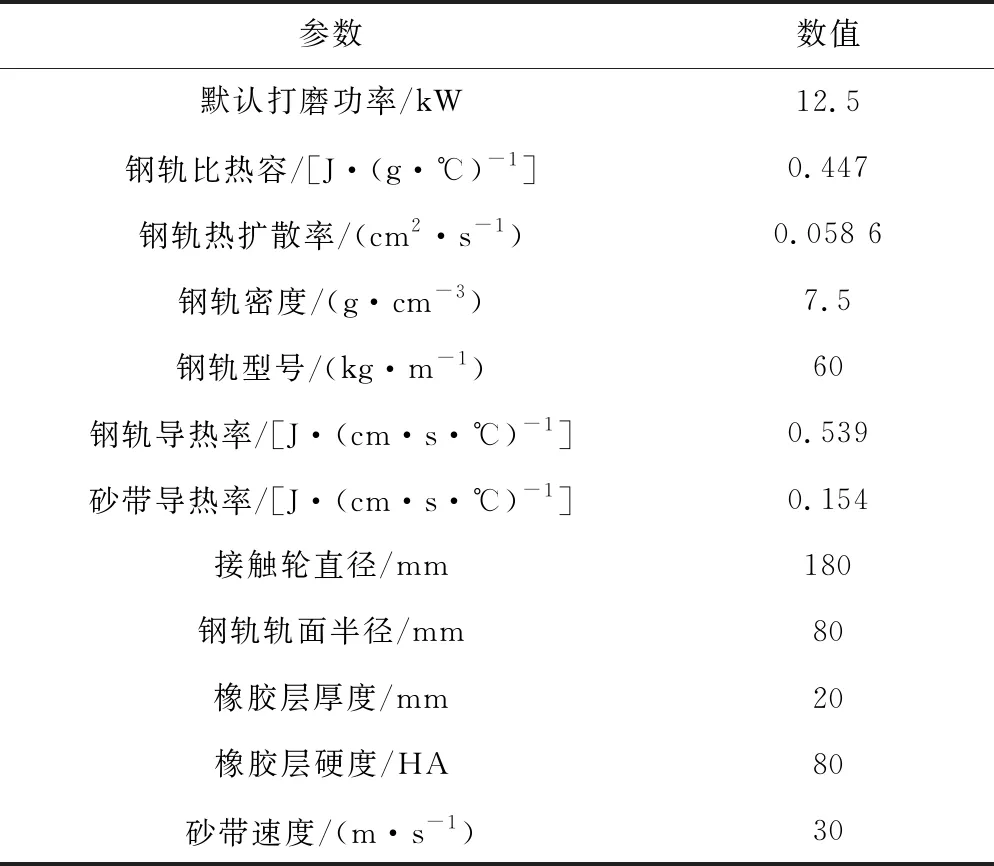
表1 仿真参数

4.1 热量传播过程

以单接触轮从坐标原点出发沿轨向进行打磨作业为例，观察不同时刻、不同位置的温度变化情况。为了减小计算量，打磨速度选为3.6 km/h，总观测时间为6 s，观测距离为6 m。仿真结果见图4、图5。

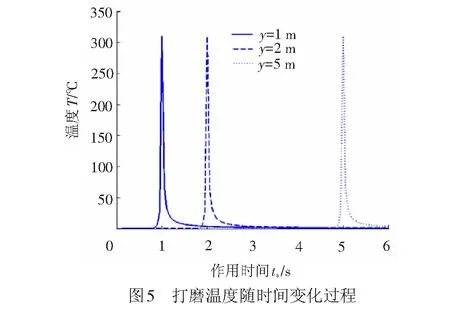
从图4可以看出，随打磨时间增长，温度峰值沿y向移动，这是因为接触区域热源随打磨小车沿轨向运动。温度峰值随打磨时间略有上升是由于模型未考虑热耗散，磨削热不断积累所致，但随时间增长，热量扩散迅速，故而增加极少。

由图5可知，对于某一位置，随时间增加，该点温度是快速增加随后缓慢降低，且温度峰值在300 ℃左右，与文献[7]中结论一致。但同文献[7]相比，数值模型打磨温度降低更快，这可能是因为数值模型考虑的是无限长钢轨，而文献[7]中有限元模型钢轨长度有限，所以文献[7]中热扩散速率较低，最终稳定的温度较高。此外，可以发现轨面温度峰值随打磨头沿运动方向同步传播。

4.2 打磨作业速度影响

以打磨初始位置为坐标原点，考察不同打磨作业速度下距离原点1 m处温度随时间的变化情况，结果见图6。

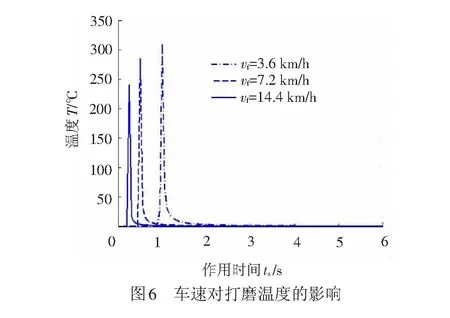
由图6可以看出，当热源不断靠近时热量加速积累，当热源远离时热量积累变缓，此时热扩散加剧，所以温度缓慢降低。此外，在相同条件下打磨小车速度越快温度增幅越小，且升温和降温幅度均更加剧烈。这是因为打磨小车速度越快，磨削区域与该点的接触时间越短，温升更低。在此短时间内进行的热量传播，不论累积或是扩散均更加剧烈。

4.3 接触轮数量影响

在钢轨砂带打磨接触部件设计时，为了有效消除钢轨波磨，需将多个接触轮刚性连接。为此，需要分析复数接触轮对打磨温度影响。在此，复数接触轮平均分配打磨压力，彼此间距为200 mm和250 mm。考量点位置y=3 m。仿真分析结果见图7。

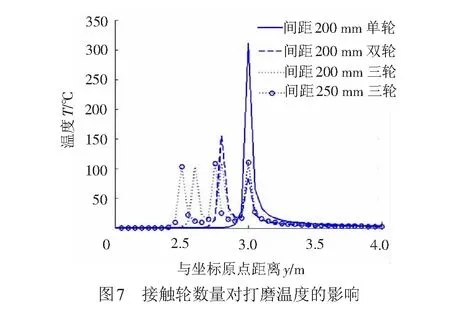
由图7可以看出，仿真结果与文献[7]有限元复数砂轮磨削热仿真结果有很好的匹配性。图7中温度波峰数量对应于接触轮个数。可以发现，接触轮数量增加可以明显降低钢轨累积温升，这表明复数接触轮不仅对消除波磨有利，对于打磨温度控制也有不错的效果。而每条温度曲线随时间呈多个波峰并逐渐累加的形式，由此推论多个联排接触轮共同作用时的温度曲线，根据速度与间隔距离配比关系可能逐渐累积也可能互不干涉。接触轮间距200 mm与250 mm对比结果可以说明，接触轮间距越大越有利于磨削热扩散，在进行接触轮结构设计时应在尺寸要求范围内适当增加接触轮间距。

4.4 轨面曲率对打磨温度的影响

以60 kg/m钢轨为例，钢轨廓形由曲率半径为300、80、13 mm三种圆弧组成。单个接触轮以相同压力(550 N)、功率分别打磨三种圆弧廓形，分析沿轨向距离3 m位置附近的打磨温度变化，仿真结果见图8。

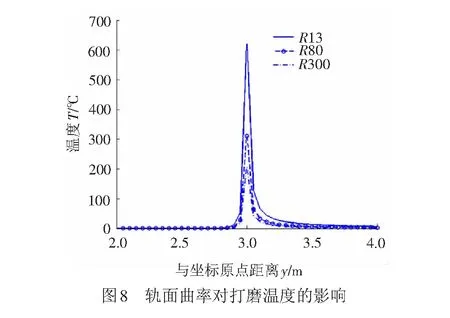
由图8可知，R13圆弧对应的打磨温度最高，R80次之，R300最低。这是因为在相同打磨压力下，R300、R80、R13弧段各自对应的接触面积分别约为896、614、300 mm2，其中R300弧段轨面与接触轮的接触面积最大，而较大的接触面积会带来较小的打磨深度和材料去除量，也意味着单位面积上产热率更低，从而热量积累相对缓慢。发热相比R80、R13两段更为均匀、分散，所以温升相对较低。而诸如钢轨内测R13的小曲率半径位置，其接触面积约为R300的三分之一，在当前设定工艺下温度峰值达到620 ℃左右，临近钢轨材料奥氏体转化温度723 ℃，当超过此温度时钢轨会出现较脆的马氏体，应当避免。虽然钢轨内侧常由于承载恶劣而变形严重，需要较大的打磨深度以修复廓形，但大切深造成的高磨削温升则易导致表面发蓝或灼烧，所以在打磨小曲率半径轨面时应适当降低打磨功，提高打磨速度以避免磨削温度过高而对轨面造成二次伤害。

5 结论

(1) 对现有钢轨打磨单点移动热源温度模型进行了修正，建立了钢轨砂带打磨温度场解析模型，仿真结果与文献[7]有限元模型分析结果匹配，说明了模型的有效性和适用性。

(2) 钢轨砂带打磨为快速升温，缓慢降温过程，提高打磨作业速度能有效缓解磨削热积累。复数刚性连接接触轮能减缓磨削热累积，且接触轮间距越大越有利于热扩散。

(3) 打磨如R13等小曲率轨面时，应通过提高打磨列车速度，降低打磨功率避免钢轨发蓝，烧伤而造成的二次损伤。