无砟轨道温度场计算及持续高温天气影响分析

康维新， 陈 帅， 魏春城， 刘学毅， 李佳莉， 刘笑凯

(1. 西南交通大学 高速铁路线路工程教育部重点实验室， 四川 成都 610031： 2. 中设设计集团股份有限公司， 江苏 南京 210001)

无砟轨道以其高稳定性、高平顺性和少维修等特点，在高速铁路上得到广泛运用[1]。作为长期暴露在自然环境中的长条状结构物，气象条件的年周期波动及日周期波动都使得轨道结构温度周期性波动[2]。现有针对无砟轨道温度场的研究主要集中在正常天气下的轨道温度特性，对于持续高温天气作用下的轨道温度尚未有人研究。已有研究成果可以按照研究手段分为试验和理论两类，其中试验测试是获取轨道结构温度特性的主要手段，杨荣山等[3]对成都地区CRTSⅠ型双块式轨道冬季温度特性进行了实测，给出了成都地区冬季无砟轨道温度荷载的取值。戴公连等[4]对桥上无砟轨道温度梯度进行了实测研究，发现轨道板表面平均日温差可达19 ℃，轨道板温度沿深度呈指数分布。赵坪锐等[5]监测了达坂城地区双块式轨道温度变化规律，并依据试验分析给出了无砟轨道温度取值方法。刘学毅等[6]、李佳莉[7]采用频谱分析方法研究了成都地区实测双块式无砟轨道温度与气象因素间的关系，给出了无砟轨道温度简便计算方法。康维新[8]实测了上海气温高达42 ℃时无砟轨道的温度特性，并针对反射隔热涂料的使用效果进行了研究。已有这些试验研究中都是在正常天气下或短暂高温天气下得到的结论，而未能证明这些试验得到的温度荷载取值方法、经验公式等在持续高温天气下的适用性。

目前对于正常天气下无砟轨道温度场的理论计算和数值仿真较少。欧祖敏等[9]推导了无砟轨道温度场日变化过程的计算公式，分析了各气象因素对无砟轨道温度的影响。闫斌等[10]建立了有限元模型，分析了轨道温度荷载模式，推荐了部分地区温度荷载值。这些研究为无砟轨道温度荷载取值提供了依据，但这些研究中建立的模型及其成果并不能直接用来研究持续高温天气的影响。在已有理论推导中，未考虑地温对轨道温度的影响，而是将其完全简化为日周期问题，这显然无法体现持续高温天气的影响；现有轨道温度仿真模型中，将轨道下部温度边界条件假设为隔热条件或某一实测的恒定温度，这种模型在计算短期温度变化是可行的，但计算时间较长时下部边界条件会发生变化，此时这种假设会带来较大误差，且轨道越深处误差越大，时间越长误差也越大。高速铁路设计规范[11]以现有研究成果为基础，将无砟轨道温度荷载分为两类，即年温差和温度梯度，但规范对于年温差的计算方法并未明确给出，对于温度梯度则简单地取正温度梯度90 ℃/m，负温度梯度-45 ℃/m，未能考虑持续高温天气的影响。为此本文根据实测气象资料，基于传热学及气象学原理，分析自然环境中无砟轨道的换热机理，推导适用于持续高温天气下轨道温度计算公式，开展试验研究，分析持续高温下无砟轨道温度特性。

1 无砟轨道结构温度场模型

1.1 无砟轨道结构温度场模型的简化

现有无砟轨道主要以板式轨道和双块式轨道为主，板式轨道由预制轨道板、CA砂浆或自密实混凝土层及支承层(底座板)组成，双块式轨道由现浇道床、预制轨枕及支承层(底座板)组成[12-14]。作为组合式结构，无砟轨道温度场实质为复杂边界条件下的层状固体三维热传导问题。

为了研究无砟轨道温度场的主要规律，需要进行适当简化。根据文献[15-16]混凝土、砂浆及各类土等材料热工参数基本一致的研究结果，不考虑钢轨和扣件影响，可认为轨道结构是热传导各向同性且均一的。无砟轨道作为长条状结构物，在一定长度内可认为其温度分布沿线路方向差别不大。此外，考虑到无砟轨道侧边与空气接触面积小，交换的热量少，仅对轨道结构的边角温度有影响，且无砟轨道材料热工参数较为稳定，随温度变化小，此时可将复杂的三维问题简化为垂向一维线性热传导问题。

无砟轨道上表面受气象变化影响，下表面(支承层或底座板下表面)受基础温度变化的影响。气象因素随时间变化规律复杂，难以用简单函数表示，这是无砟轨道温度场计算的一大难点。无砟轨道下表面温度除实测外，难以直接获取。由于无法给出下表面边界条件，故数值方法难以根据实测气象资料全面计算无砟轨道温度场，这也是轨道结构温度计算和预估的另一大难点，为此本文将无砟轨道简化见图1，只有上表面的半无限空间体，以解决下表面温度未知的困难。

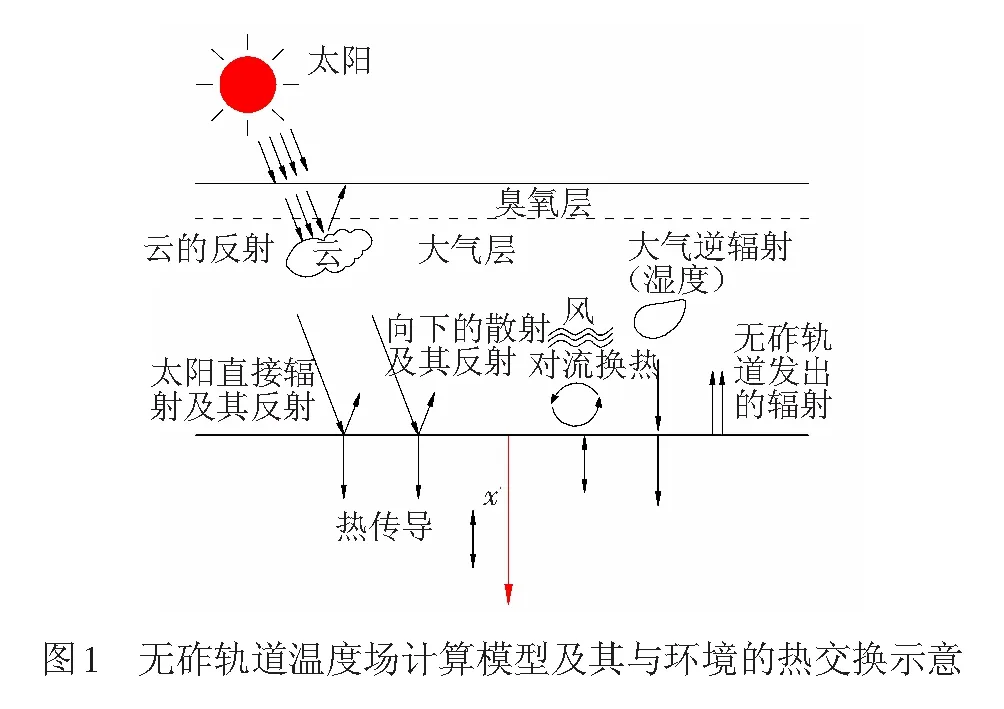
1.2 无砟轨道与环境的热量交换

1.2.1 太阳辐射

太阳辐射是无砟轨道的主要热量来源，到达地球的太阳辐射强度相对恒定，波动很小，但无砟轨道表面能够接受到的太阳辐射受大气、地理位置等因素影响很大。进入大气的太阳辐射一部分被云层反射回宇宙空间(见图1)，一部分被臭氧、水蒸气等吸收，一部分被空气分子及尘埃向各个方向散射，剩余的部分(太阳直接辐射)以一定的角度照射到地表上，即到达地表的太阳辐射为天空散射的一部分和太阳直接辐射的总和。混凝土并不是绝对黑体，照射在其上的太阳辐射有些会被反射掉。混凝土的太阳辐射吸收系数受其表面亮度、平整度及脏污程度等的影响程度较大，取值为0.5～0.7[17-21]。研究表明[22-23]：混凝土新浇筑时取0.5；使用时间较长时取0.7。太阳辐射带给无砟轨道的热流密度为

qs=asQ

( 1 )

式中：qs为太阳辐射折算后的热流密度，W/m2；as为轨道表面的太阳辐射吸收系数；Q为单位面积上的太阳辐射，W/m2。

1.2.2 大气

对流热交换和红外电磁辐射换热是物体与空气热交换的主要手段。

(1) 对流换热及风的影响

由冷却定律知，对流形式的热流密度为

qc=uc(Ta-Ts)

( 2 )

式中：qc为对流热流密度，W/m2；Ta为气温，℃；Ts为轨道表面温度，℃；uc为对流系数，W/(m2·℃)。

对流系数受风速影响很大，算式为[24]

( 3 )

式中：v为日均风速，m/s。

(2) 辐射换热

现代物理学表明物体内粒子的热运动运动导致表面在持续的辐射电磁波，温度越高辐射能力越强，波长越短。大气温度和无砟轨道表面温度远低于太阳温度，它们发出的辐射波长大于太阳辐射的波长，称为长波辐射。大气向各个方向发射长波辐射，朝向地表的部分称为大气逆辐射,见图1。大气逆辐射与无砟轨道表面间的差值称为有效辐射。由Stefan-Boltzmann式[25]，以有效辐射形式进入无砟轨道的热流密度为

ql=εaσ(Ta+273.15)4-εsσ(Ts+273.15)4

( 4 )

式中：ql为有效辐射热流密度，W/m2；σ为5.67×10-8，W/(m2·℃4)；εs为黑度系数，本文取0.88；εa为大气黑度系数，受湿度、大气温度及云量等影响，取值范围在0.8～0.9，为简化计算，本文取为0.88。

利用平方差公式，将式( 4 )展开后写成对流换热的形式，即

ql=ul(Ta-Ts)

( 5 )

( 6 )

大气带给无砟轨道的总热流密度为

qz=uz(Ta-Ts)

( 7 )

uz=

( 8 )

式中：qz为由大气与轨道间的总热流密度，W/m2；uz为总热交换系数，W/(m2·℃)。

综上所述，自然环境下无砟轨道表面的热流密度可表达为

q=qs+qz=

( 9 )

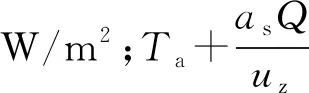
2 无砟轨道温度场的求解及修正

2.1 气温和太阳辐射的函数表示

以往研究中多采用半波正弦来表示完全晴天时到达地表的太阳辐射日变化过程，对比实测资料发现，即便是晴天，太阳辐射日变化与半波正弦也有较大差别，而有云天、阴天则差别更大，显然采用这种简单函数表示的太阳辐射日过程无法准确分析无砟轨道温度场。与太阳辐射日变化类似，以往研究中多采用正弦函数模拟气温日变化过程，这种方法模拟白天气温变化较为准确，而夜间误差较大。事实上大气温度受很多因素影响，其日变化规律非常复杂，晴天与阴天不同，不同地区不同，不同季节也不相同。由于气象资料都可通过各地气象站方便获取，假设ci和di(i=0,1,2,3,…,24)分别表示τ=0,1,2,3,…,24时测得的气温和太阳辐射强度，则采用傅里叶级数可建立太阳辐射和气温表达式

(10)

(11)

(12)

(13)

式中：Q为太阳辐射强度，W/m2；Ta为气温，℃；an、bn分别为太阳辐射、气温的傅里叶级数系数；n为无穷级数项数；τ为时间，h。

2.2 无砟轨道温度场的求解

若记无砟轨道各深度处温度为T，则其应满足[25]

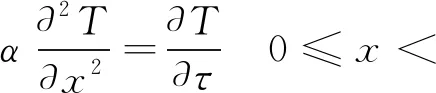
(14)

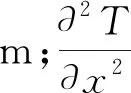
(15)

x=T≠

(16)

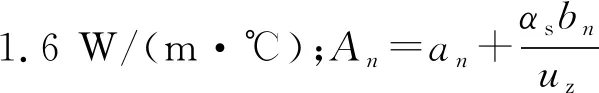
求解式(14)，得轨道温度

(17)

(18)

(19)

(20)

(21)

式中：Sn为轨道表面温度幅值与等效气温的比值；βn为轨下结构深度x处温度波动幅度相对表面温度波动幅度的比值；φxn为x深度处温度相对表面温度的滞后相位；φsn为表面温度相对等效气温的滞后相位。当n取不同值时，得到βn与x的关系，见图2。

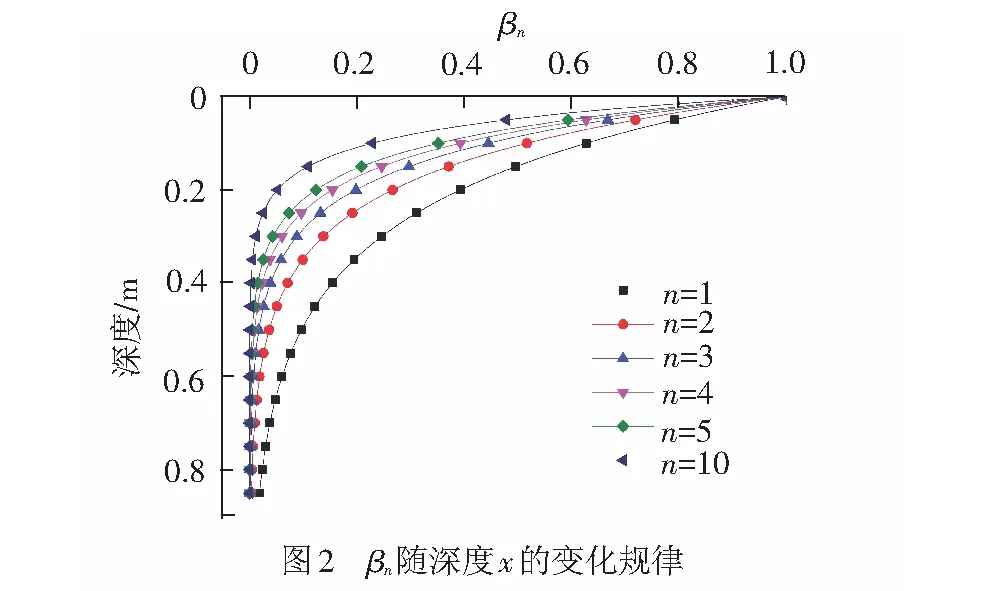
当x≥0.85 m，n≥1时，βn=0，式(17)变为

Tx≥0.85=A0

(22)

式中：Tx≥0.85为轨下结构深度0.85 m及以下的温度，℃；A0为等效气温的平均值，℃。

式(22)表明，轨下结构深度0.85 m及以下处温度与外界因素日变化无关，称此处温度为地温。实际上，地温由气象因素年变化决定。

2.3 地温修正

除地球自转导致气象因素日周期变化外，地球绕太阳公转也会使得气象因素产生年周期变化，年变化对无砟轨道表面温度影响不大，但随着深度增加，气象年变化逐渐取代日变化，成为决定无砟轨道温度的主要因素。

由前述分析知，地温与气象因素的日变化无关，由年变化决定。若已知365 d的逐日平均气温和平均太阳辐射，应用前述类似方法可求得轨下结构深度0.85 m处温度为

(23)

(24)

(25)

式中：Syn、φsy与Sn和φsn类似，分别为轨道表面温度年变化幅值相对等效气温年变化幅值的比值和滞后相位；Ayn为年等效气温的振幅，℃；αy为混凝土以日为单位的导温系数，0.072 m2/d；uzy为以年平均风速和年平均气温代入式( 8 )算得的总换热系数，W/(m2·℃)；τy为时间，d。

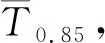
(26)

式中：Tc为某一深度处温度修正量，℃。

故无砟轨道温度场最终解为

(27)

而各深度处的日平均温度可由等效气温日平均值与地温线性插值得到

(28)

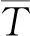
3 无砟轨道温度计算公式的验证

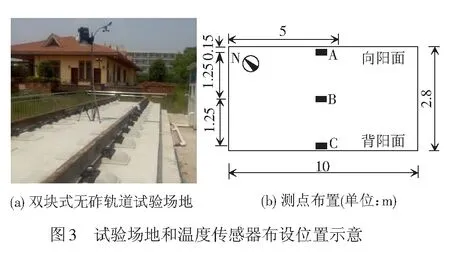
为研究无砟轨道温度场的特性，修筑了长10 m的CRTSⅠ型双块式轨道，轨道走向为北偏西37°, 见图3(a)。试验地点位于成都(104°1′E，30°5′N)，海拔500 m，常年风速较低，气候湿润，夏季日照较多，冬季日照较少。按图3(b)所示位置在道床板上下表面及距离上表面0.16 m深度处布置铂电阻温度传感器监测轨道温度，并在轨道上安装了气象站，对气象参数进行监测。

2015年8月21日—2016年8月21日的日平均太阳辐射强度、日平均气温见图4(a)，该段时间平均风速约为1 m/s。2016年8月21日太阳辐射、气温见图4(b)，当日平均风速0.3 m/s。由于试验是在该段无砟轨道修筑好两个月后开始监测温度，此时混凝土尚新，太阳辐射吸收系数取0.5。

利用式(23)、式(28)分别算得2015年8月21日—2016年8月21日的地温和道床板中部温度，见图5(a)。式(28)算得试验期间道床板表面和板底面日平均温度与实测值的对比见图5(b)。

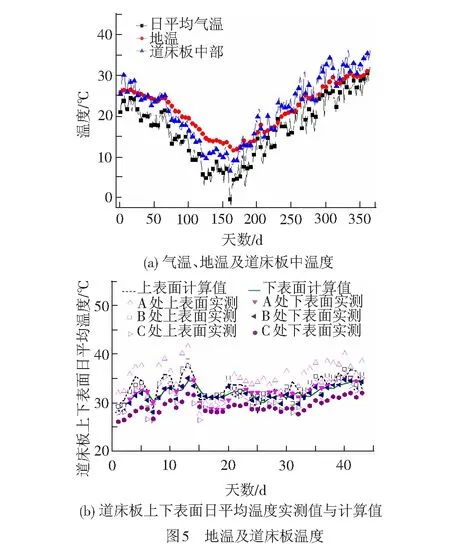
图5(a)表明，地温变化趋势与日平均气温变化趋势一致，但变化幅值有所减小，道床板内部温度由于受太阳辐射的影响，日平均温度高于气温，年变化幅度约为40 ℃，故成都地区无砟轨道年温差可取40 ℃。图5(b)表明，道床板向阳处的日平均温度最高，板中温度次之，背阳处日平均温度最小，但变化趋势一致。无砟轨道上下表面日平均温度计算值与实测值吻合较好，证实了本文提出的无砟轨道各深度日平均温度计算公式的准确性。

应用式( 8 )算得当日的总换热系数uz为13.1 W/(m2·℃)，算得等效气温见图4(b)虚线，最大值达60 ℃。8月21日地温为30 ℃，应用式(27)可计算道床板上下表面及深度0.16 m处的温度，将其与道床板相应测点的实测温度对比，见图6。

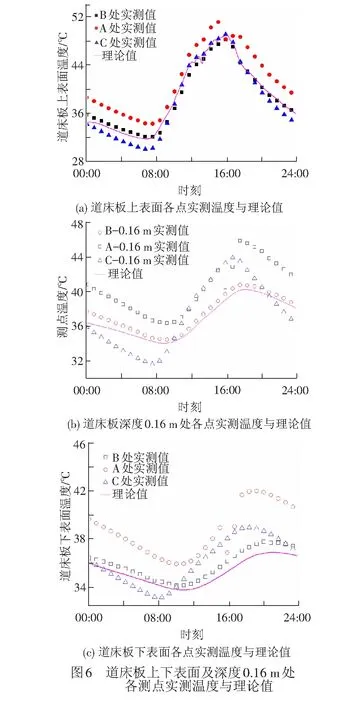
图6表明向阳侧(A处)道床板温度整体高于背阳侧(C处)温度约3 ℃，但板边处温度变化趋势与板中心处(B处)温度变化趋势一致。由图6可知，道床板中心上下表面、道床板中部温度的理论计算值与实测值吻合较好，说明本文推导的公式能够有效计算无砟轨道温度场。

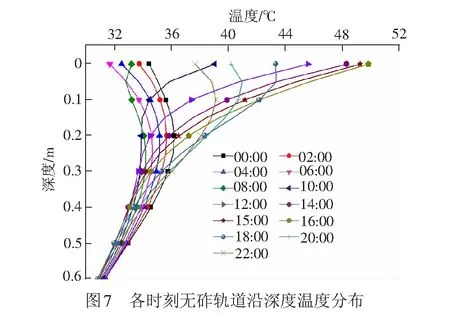
根据式(27)算得当日不同时刻轨道温度分布见图7。由图7可得，轨道表面温度波动18 ℃， 0.2 m处6 ℃，下表面约4 ℃。无砟轨道在0～0.2 m深度内日温度变化较大，容易出现较大温度梯度。凌晨0:00到8:00，道床板下表面温度较高，道床板呈负温度梯度，支承正温度梯度。6:00时出现负温度梯度极值-15 ℃/m。8:00时受太阳影响，轨道温度快速上升，16:00时正温度梯度达到极值，为70 ℃/m。16:00至次日凌晨0:00，道床板表面温度逐渐降低，热量集聚在道床板内，形成道床板中心温度高，上下表面温度低的非线性分布。

4 持续高温天气下的无砟轨道温度场

气象学根据人体适应性，将高温天气分有蓝、黄、橙、红级别，最高气温连续三天超过35 ℃时称为黄色预警。2013年夏季长江下游地区连续50多天最高气温超过35 ℃，部分无砟轨道出现上拱等病害，给行车带来巨大安全隐患。

杭州2013年日平均气温和太阳辐射见图8(a)，最热当天的逐小时太阳辐射强度、气温和等效气温见图8(b)，杭州当年平均风速1.5 m/s，持续高温期间风速0.3 m/s，太阳辐射吸收系数取0.5。

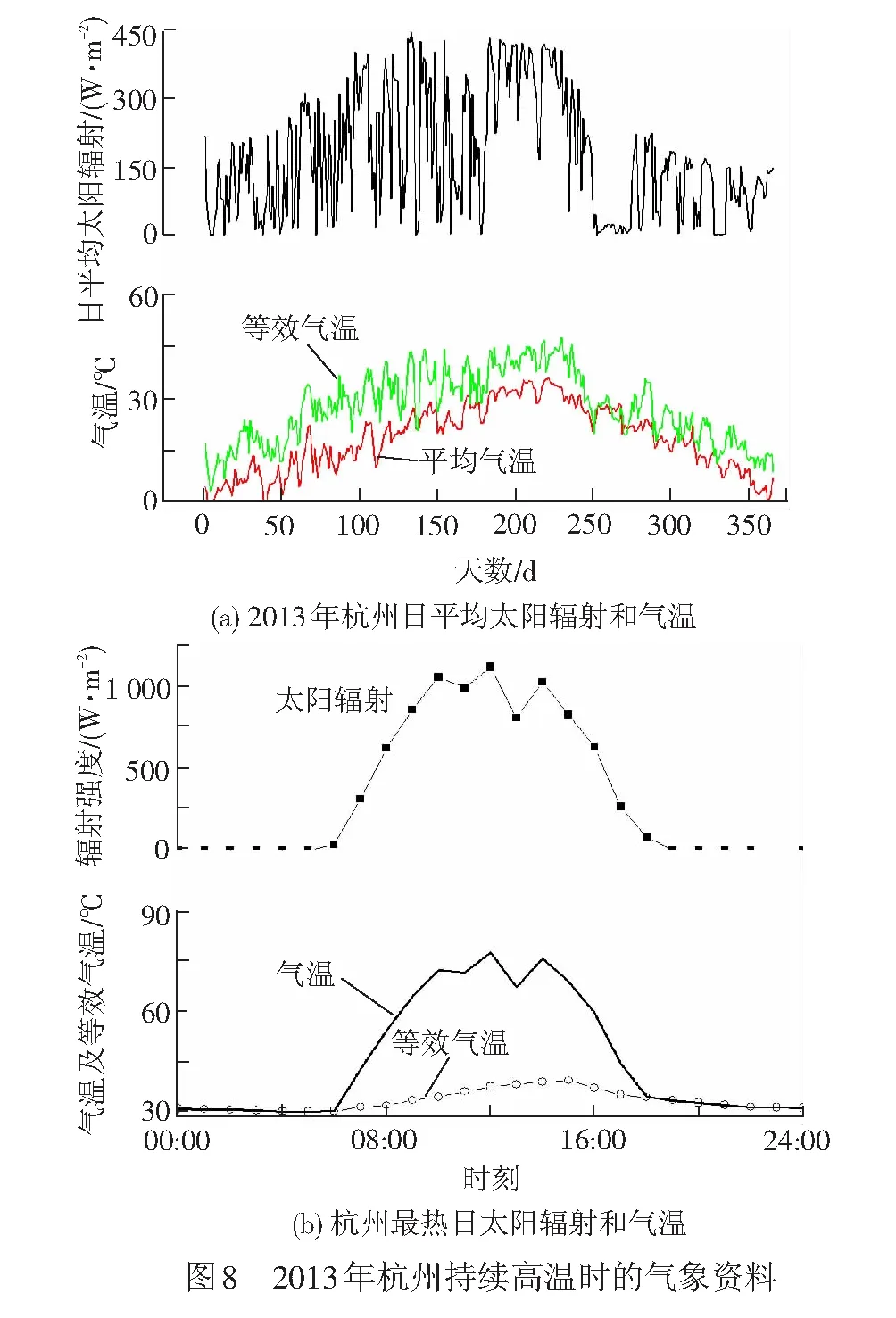
图8(a)表明，杭州地区从2013年第180 d到第230 d，日平均太阳辐射强度在400 W/m2左右，日平均气温约为35 ℃，是典型的持续时间很长的高温天气，图8(b)表明最热一天最高气温超过40 ℃，正午太阳辐射达到1 100 W/m2。

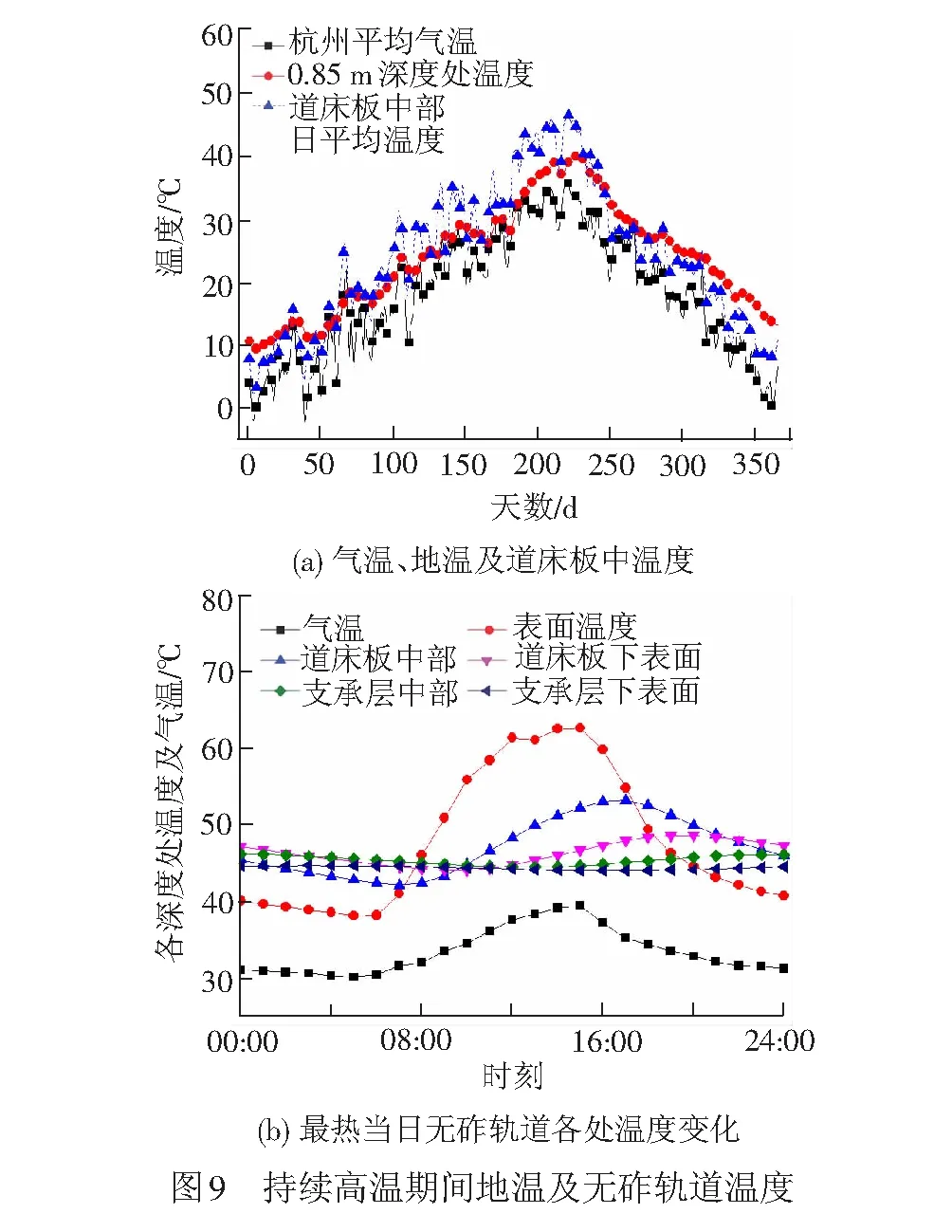
利用气象资料，以双块式轨道为例算得杭州地区2013年地温及道床板中部温度见图9(a)，从第180 d开始，地温随日平均气温的上升而持续上升，最热当日地温达到42 ℃，道床板中最高日平均温度更是达到47.5 ℃，远高于日平均气温。最热当日各深度处温度变化见图9(b)，无砟轨道各深度处温度远高于气温，表面最高温度达到65 ℃，支承层温度达到46 ℃。道床板表面日温差达25 ℃，道床板中部日温差12.5 ℃，支承层日温度变化较小，温差较小。

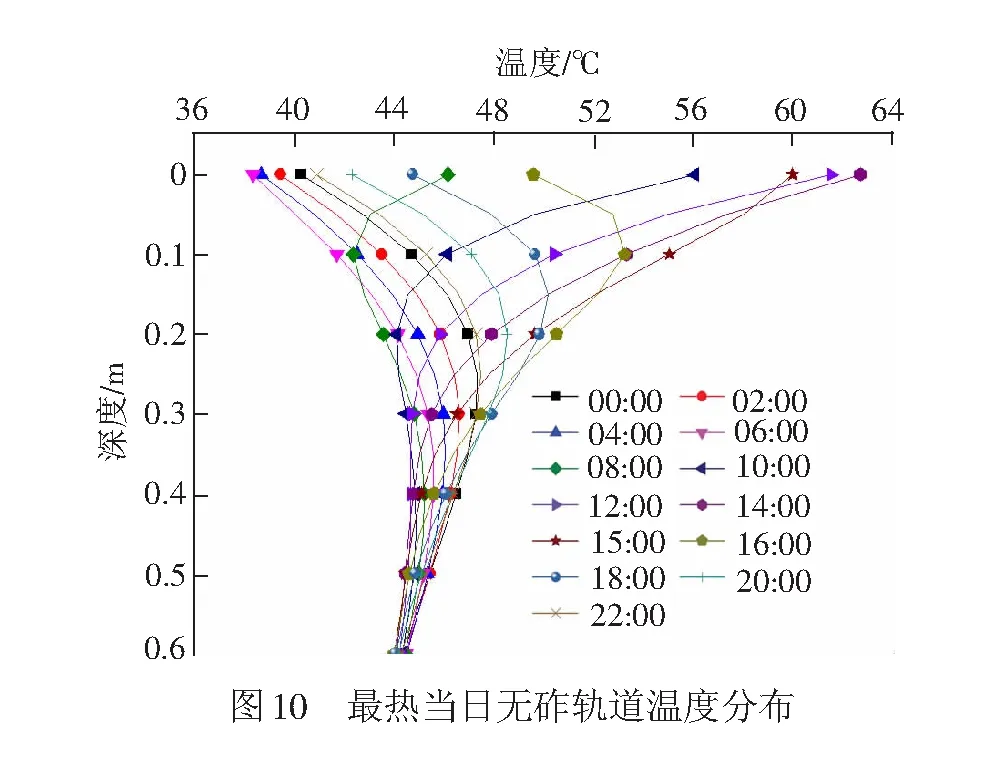
利用式(27)可算得最热当日各深度处温度分布见图10。相比图7，持续高温下的无砟轨道温度分布主要特点是：下部基础温度高，无砟轨道整体温度偏高。在杭州持续高温下，轨下结构深度0.2 m范围内，日最大正温度梯度达到100 ℃/m，高于TB 10621—2014《高速铁路设计规范》[11]规定值，日最大负温度梯度达到-30 ℃/m。

对2013年持续高温下无砟轨道温度场的计算表明：持续高温期间天气持续晴朗，太阳辐射持续较强，平均气温持续上升，无砟轨道整体温度也随之上升，由于太阳辐射的影响，无砟轨道整体温度远高于气温。道床板中部温度高于气温15 ℃，最高可达55 ℃，日均温度为46 ℃。在持续高温天气下，无砟轨道除了整体温度升高外，其正温度梯度也高于规范规定90 ℃/m。

由上述分析可以看出，气象学上对于持续高温的定义较难适用于无砟轨道温度。对于无砟轨道，不仅要关注最高气温，而且要关注日平均气温，当出现高温天气时，若日平均气温也较高时就要注意无砟轨道的整体温度，预防道床板/轨道板上拱等病害的发生。

5 结论

本文在分析无砟轨道与大气环境换热机理的基础上，考虑了气象日变化、年变化及地温对轨道温度的影响，推导了基于气温、风速及太阳辐射的无砟轨道温度场计算公式，开展实测验证，计算分析了持续高温天气下无砟轨道的温度特性。

主要结论为：

(1) 忽略钢轨扣件等的影响，将无砟轨道简化为受周期性热边界条件影响的导热均质半无限空间体，能够较为准确有效地计算无砟轨道温度特性。

(2) 无砟轨道温度不仅受气象日变化影响，而且受气象年变化的影响。气象日变化主要影响深度小于0.85 m的温度，气象年变化主要决定深度大于0.85 m的温度(即地温)，计算无砟轨道温度时，应考虑气象年变化造成的地温修正。

(3) 持续高温天气时，日平均气温很高，导致无砟轨道下部基础温度(地温)较高，地温能够达到42 ℃，热量难以向下传递。无砟轨道整体温度升高且远高于气温，可比气温高约15 ℃，而且出现较大的温度梯度，最大正温度梯度能够达到100 ℃/m。