交通荷载引起的静偏应力对压实黄土动力特性的影响

2019-08-20胡志平赵振荣李小乐

铁道学报 2019年7期

王瑞，王雷，胡志平,3，赵振荣，李小乐，王强

(1．长安大学建筑工程学院，陕西西安 710061； 2．中铁西安勘察设计研究院有限责任公司，陕西西安 710054；3．长安大学地下结构与工程研究所，陕西西安 710061)

相较于静力荷载，动力荷载对岩土材料的承载力和稳定性影响更为显著。在动力荷载作用过程中会出现诸如液化、失稳等一系列工程问题。动力加载过程中，岩土介质的动应力-应变关系是直接反映材料宏观动力特性的重要参数之一，也是开展场地地震反应分析、求解动力荷载下地基基础动力响应的必要条件。在研究动应力-应变关系时，需要结合荷载的特点设计相应的加载时程，如地震荷载主要以垂直传播的剪应力为代表，交通荷载具有一定的静偏应力并伴随着主应力轴的旋转，波浪荷载则多为简谐荷载且伴随着主应力轴的旋转。以往大部分的研究工作均集中在地震工程领域，并没有考虑交通荷载作用下的静偏应力对土体动力本构关系的影响[1-3]。近年来，公共交通事业飞速发展的同时也对路基在长期动力荷载作用下的稳定及变形特性提出了更高的要求。为揭示交通荷载引起的静偏应力对土体动力特性的影响，相关领域的研究者在已有试验手段的基础上开展了系列的研究工作。王常晶等[4]和蔡袁强等[5]通过开展饱和软黏土的动三轴试验指出交通荷载引起的静偏应力对软土的动力特性影响显著。Zhu等[6]通过分级加载形式研究了列车荷载作用下北麓河冻土的动力特性。Wang等[7]通过GDS空心圆柱系统研究了交通荷载引起的静偏应力对原状黄土动力特性的影响规律。罗飞等[8]通过分级加载研究了静偏应力作用下冻结兰州黄土和青藏黏土的动力特性，在考虑塑性应变的前提下定义了新的动模量计算方法。周文权等[9]考虑列车荷载偏应力研究了低围压循环荷载作用下饱和粗粒土的动应力-应变关系。根据现有研究结论，考虑静偏应力时土体塑性变形发展加快，相同应变水平下的动模量明显提高。

除此之外，运营期内交通荷载的重复作用势必影响路基土体的动力特性。因此，研究循环荷载的振次对土体动力特性的影响规律具有一定的现实意义[8]。在不考虑静偏应力时，土体的动模量往往随着振次的增加逐渐衰减且模量折减系数与振次在双对数坐标内呈线性关系[10-11]。周文权等[9]指出考虑静偏应力时，随着循环周次的增加，滞回圈斜率增大，土体动模量增加。导致动模量随振次变化规律差异的根本原因是累积应变的产生。在长期列车荷载作用下，静偏应力导致的累积应变也是交通工程领域关注的重点。国内外针对饱和砂土、软黏土、冻土和粗粒土在长期交通荷载作用下的累积应变规律开展了系列试验研究，得到了很多有意义的成果[12-15]。理论研究方面，除经典的指数模型等经验预测模型之外[16]，研究者将土体的累积应变看做动力蠕变[17-18]，将振次等效成时间变量，利用描述材料蠕变的元件模型建立了长期列车荷载作用下土体的累积应变预测模型[19-20]。在此基础之上，高广运等[21]通过线性叠加法建立了动荷载作用下土体的蠕变本构方程，采用分层总和法求解了列车荷载作用下地基的长期沉降。吴志坚等[22]基于现场实测数据和冻土的三轴流变试验结果，通过蠕变分析得到了列车荷载作用下冻土路基的长期变形。

虽然随着青藏铁路和高速铁路的建设开展了一系列研究工作，但针对交通荷载下土体动力特性演化规律的研究基础依然较为薄弱。已有的研究大都是针对饱和砂土、软黏土和冻土开展的，对于压实黄土路基在交通荷载下动力特性的研究还比较少见。近年来，由于国家西部政策的推进，黄土地区的基础设施建设不断完善。由于地形限制，兰州和延安相继开展了大规模的“开山造地”运动，黄土填方区域动辄几十平方公里。因此，研究长期交通荷载作用下的静偏应力和循环振次对压实黄土动力特性的影响规律具有重要的工程实践意义。此外，本文基于动力蠕变思想阐述了动力加载阶段滞回圈的“不闭合”现象并对其进行了修正。

1 试验介绍

1.1 试验仪器

本次室内试验采用英国产GDS动三轴试验系统(DYNTTS)。系统由GDS公司开发的GDSLAB软件控制，可以施加正弦波、半正弦波、三角波和用户自定义波形，选择差压传感器精确控制低固结应力，通过直接闭环控制轴向位移、偏应力、围压和反压。

1.2 试样制备

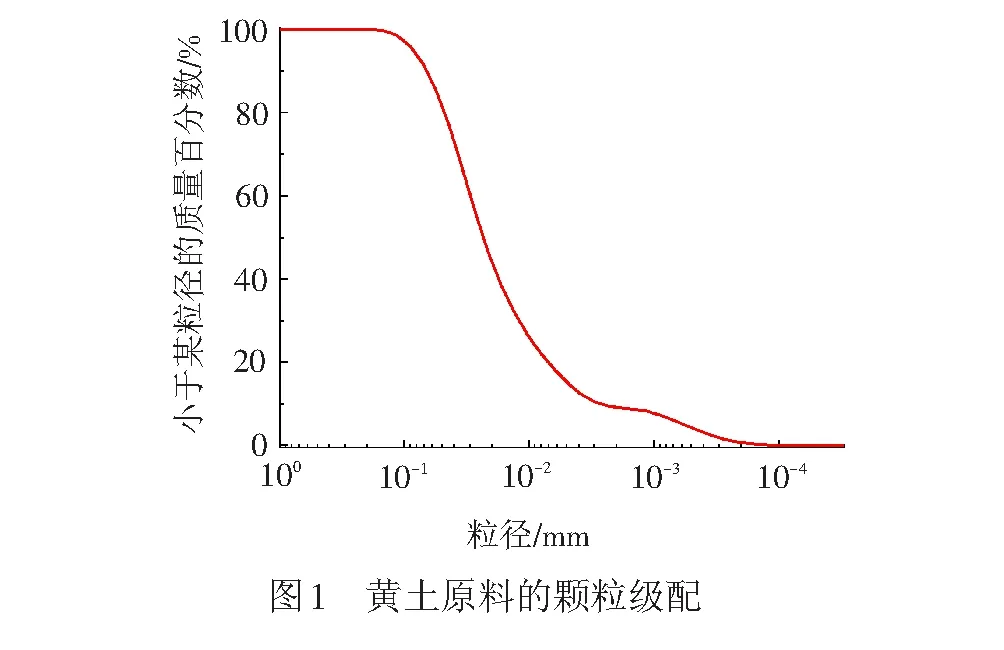
制样过程[23]：制样前将土烘干，木槌捣碎过0.5 mm筛；添加蒸馏水至最优含水率并拌匀后密封放置在保湿缸中养护一昼夜，使其充分浸润；将土样分5层压成直径58 mm、高100 mm的圆柱形土样，每层之间拉毛使其充分接触；最后削成直径38 mm、高76 mm的圆柱形试样，保鲜膜包裹后称重并放入保湿缸备用。过程中控制压实度为0.95。

1.3 试验方案

本次试验参照文献[24]相关规定进行。试验采用应力控制加载，输入频率为1 Hz的正弦波模拟交通荷载[4]。为研究静偏应力对压实黄土动力特性的影响规律，在围压100 kPa情况下设置静偏应力分别为0、80、240、400 kPa。加载示意见图2，图2中：N为每级振次；σs为静偏应力；σd为动应力幅值。

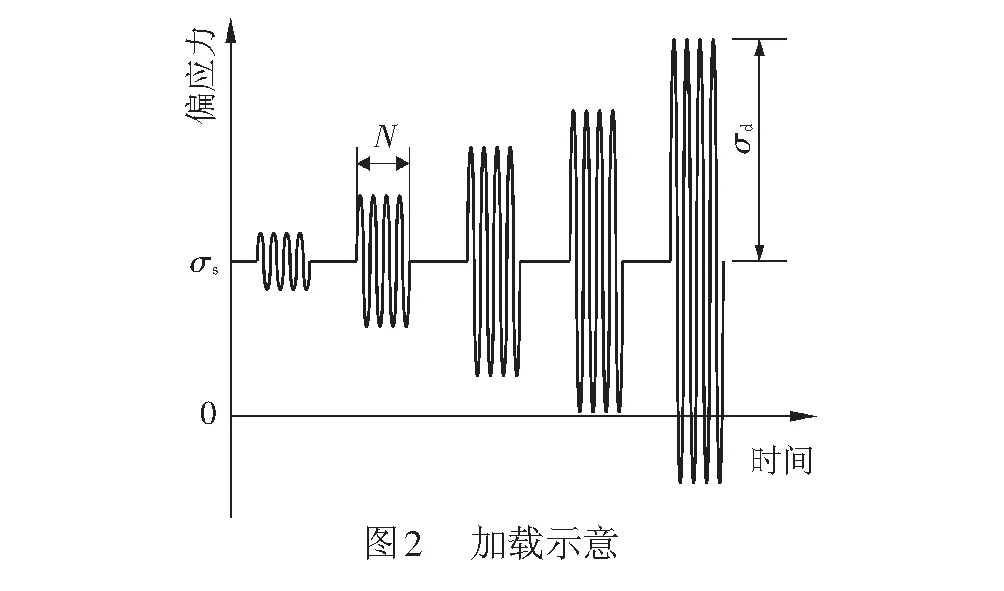
静偏应力为0 kPa时(常规工况)采用分级加载。考虑到分级加载的级数一般都大于20，较大的振次会显著增加单个试样的加载时长，每级荷载对土样的扰动也会逐渐显著，每级振次分别设置为10次和1 000次。逐级加载时荷载递增的幅值一般取4 kPa，两次测试的振级均为22级。加载过程中根据实际情况对加载幅值进行适当调整，如每级振次1 000次工况的加载后期，试样动应力-应变曲线渐趋平缓，则适当减小幅值增量以提高测试精度。当静偏应力不为0 kPa时，考虑土体动力蠕变对其的扰动，采用单级加载，振次取为1 000次。具体工况设置见表1。

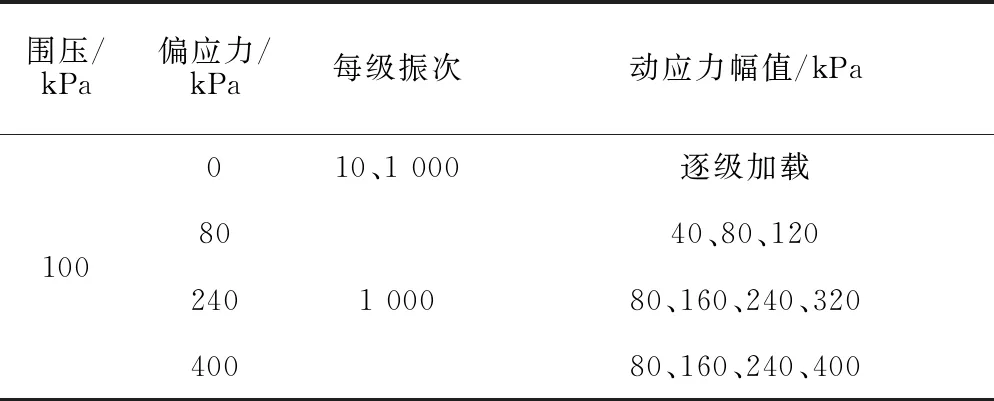
表1 压实黄土试验工况设置

试验时首先采用等向固结施加围压，过程中保持排水阀始终开放，设置1 h内轴向应变变化不超过0.05%为固结的结束条件。之后关闭排水阀，在1 min内将轴力均匀加至预设静偏应力值，施加完毕后即开始施加动应力。除了将振次作为试验结束条件之外，为了防止土样由于过度压缩而撑破橡皮膜，试验过程中设置双幅应变达到10%为备用结束条件。

2 结果分析

2.1 动应力-应变关系

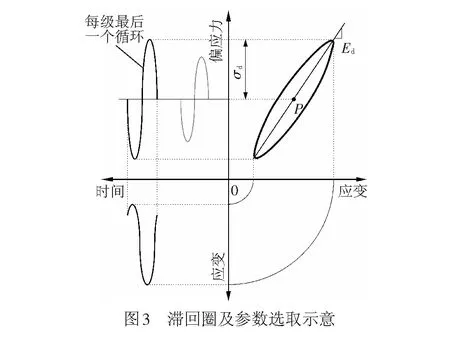
选用每级加载的最后一个滞回圈为代表见图3(图3中Ed为动应力-应变关系的割线模量)，提取滞回曲线时将坐标轴中心平移至当前滞回圈的几何中心(P点)，建立压实黄土的动应力-应变关系曲线和动模量随动应变幅值的变化规律[1],见图4、图5。

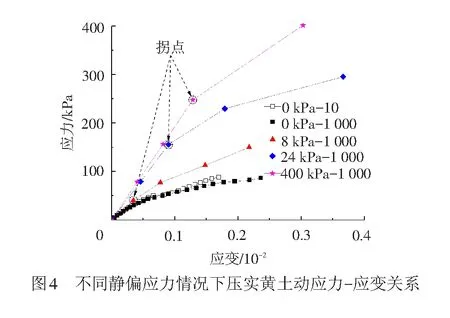
通过对比可以看出，静偏应力对压实黄土的动应力-应变关系影响显著。随着静偏应力的增加，相同动应变幅值下压实黄土的动模量显著增加。当静偏应力较小时(80 kPa)动模量随着动应变幅值的增加近似呈线性降低；随着静偏应力的增加(240 kPa)，在较小的动应变水平下动模量近似为定值，即土体的动应力-应变关系近似表现为线性，随着动应变的逐渐增加，动模量再次随着动应变幅值的增加近似呈线性降低；随着静偏应力的进一步增加(400 kPa)，动应力-应变关系呈现线性段的动应变区间进一步扩展。与典型的双曲线应力-应变关系相比，考虑静偏应力之后随着动应力的增加，动模量的衰减变得更为困难，并且静偏应力越大，动模量开始衰减时需要的动应力值(图4中的拐点位置)越大。出现上述现象的原因可能是静偏应力的作用导致土体结构逐渐趋于密实。可以认为，当考虑静偏应力对压实黄土动力特性的影响时，描述土体动应力-应变关系的经典双曲线模型不再适用。

对比静偏应力为0 kPa时不同每级振次(10和1 000)工况下的骨干曲线可以看出，在应变较小时两种工况下测定的动应力-应变关系曲线总体一致，但随着动应变幅值的增加，两种工况测得的动模量之间的差异逐渐显现。与每级振次为10的工况相比，每级振次为1 000时测得的动模量逐渐变小。也就是说，振次的增加可能会导致土体的刚度逐渐软化。

为提高教学质量，首先教师要结合学生的情况，制定合适的教学方案，然后再把学生分成不同小组，并选择基础比较好的学生担任小组组长。在每一节课程中，教师可以选择不同层次的问题引导，让学生们可以在小组探索中发挥自身的优势，形成共同探索的一种氛围。由于学生们都有自己喜欢的部分，通过小组成员之间的感染，可以形成互助学习的氛围，调动学生的学习积极性。

对于每级振次对动应力-应变关系的影响，考虑到在大应变条件下振动次数的累积会导致动应变的较大变化，文献[25]建议在测试土的动力特性时采用多个试样独立测定不同动应力下的动应变。尚守平等[26]通过应变控制的循环单剪试验研究了大应变条件下(>10-3)应变累积效应对饱和粉质黏土动力特性的影响，指出由于存在“记忆消失”现象，先前的较小幅值的循环荷载对后继较大幅值荷载下土体的动力响应影响较小，验证了逐级加载方式的可行性。本文逐级加载结果显示，每级加载振次的变化对压实黄土的动应力-应变关系有一定的影响，随着动应变幅值的增加，振次较少工况下土体的动模量有略微增大的趋势，但不太明显。

2.2 振次对动模量的影响规律

为探讨各级荷载作用下振次对压实黄土动力特性的影响规律，绘制动模量随加载振次的发展趋势见图6。静偏应力作用下随着振次的增加，各级荷载下土体的动模量有逐渐增加的趋势，静偏应力为80 kPa时增加的最为明显。此时动模量的逐渐增加可能是因为静偏应力的作用使土体逐渐被压密。2.1节已经指出，静偏应力的作用会导致压实黄土的动应力-应变关系在较小的动应变水平下近似表现为线性。通过进一步探讨振次对各级荷载下动模量的影响规律，发现在较小的动应力水平下，振动刚开始时的动模量具有一定的离散性，随着振次的增加逐渐趋于一致，见图6(c)。

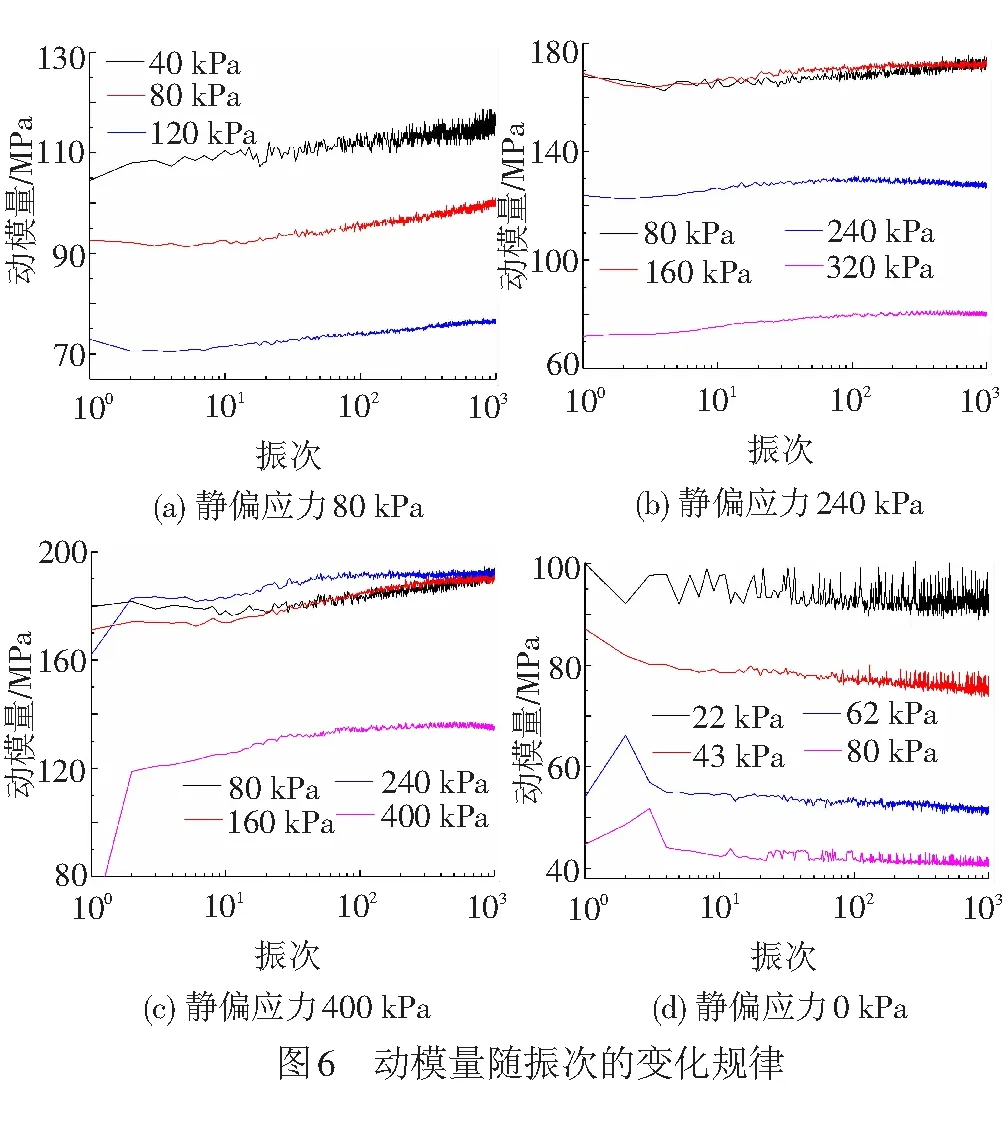
上述规律显示，在考虑静偏应力作用时，土体的动应力-应变关系在一定的起始应变区间内具备呈线性变化的“潜质”，只是由于制样、装样等操作差异导致其动力特性在荷载作用初期不太稳定(由于逐级加载时始终采用同一试样，结果的稳定性一般较好)。后期随着振动次数的增加，土体内部结构通过不断的调整最终趋于稳定。除此之外，通过图6(a)和6(d)还可以看出，当动应力幅值较小时(40、43 kPa)，加载后期土样的动模量震荡较为明显；随着动应力幅值的增加，动模量逐渐趋于稳定。另外，当静偏应力为0 kPa时，压实黄土的动模量随着振次的增加逐渐衰减，与考虑静偏应力情况下的变化情况完全相反。因此，常规不考虑静偏应力情况下得到的土体的动力本构参数并不适用于研究交通荷载下路基的动力响应。与此同时，由于常规情况下路基断面随列车运行方向的变化不大，2.5D有限元等频域分析方法在铁路工程中得到了广泛的应用，其中路基土体在动力荷载作用下的非线性应力-应变关系成为了制约频域计算方法的关键问题[27]。本文关于压实黄土在静偏应力作用下动应力-应变关系在一定应变区间内呈线性变化的相关发现可能会进一步推动频域分析方法在分析黄土地区铁路路基动力响应中的应用。

2.3 基于蠕变的动模量修正

由于振动过程中塑性变形的存在，滞回圈的中心会存在偏移。以往的研究多是简单的将坐标轴中心平移至相应滞回的几何中心来建立土体的骨干曲线，并未考虑由于土体塑性变形产生的滞回圈“不闭合”现象[1,9]。尤其是考虑静偏应力的影响时，土体的塑性变形更为显著，其对土体动力特性的影响不容忽视。国外相关规范也规定，当某一滞回圈的残余应变大于0.2%时，该滞回曲线不能用来定义土体的动模量[28]。众多文献表明，土体在交通荷载作用下的塑性变形机制可以归结为动力蠕变[17-18,20-21]。将交通荷载下土体的变形和动力学特性问题分开考虑不仅有助于明确研究思路、简化工程应用并且更容易将试验结果合理引入到现有的有限元及理论计算当中。

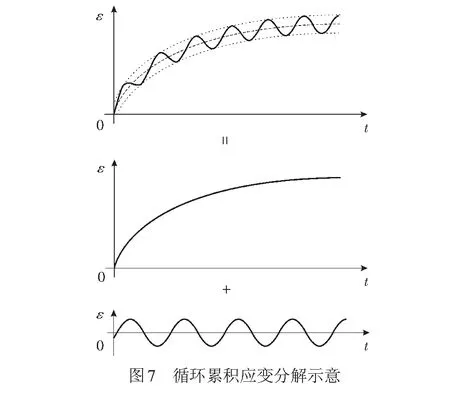
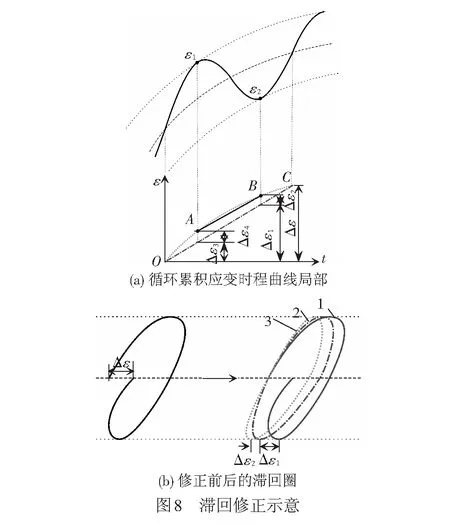
基于上述考虑，本文将土体在静偏应力作用下的循环累积应变分解为动力蠕变和弹性应变，并对其滞回特性进行修正(图7)。将每振次产生的塑性应变看做动力蠕变，通过消除原始滞回中的蠕变分量得到可以反映土体黏弹性动力特性的闭合滞回圈，在此基础之上进行动力分析，修正示意见图8。图8(a)为局部循环累积应变时程曲线，曲线OABC为一个滞回内的等效蠕变曲线；图8(b)为修正前后的滞回圈，定义图中的Δε为每循环产生的动力蠕变，图中1号线为原始滞回圈。修正时按照等效蠕变曲线将Δε分解到循环累积应变的各点即可以得到图8(b)中3号线闭合滞回圈(点线)。在进行实际操作时，由于单个振次内的实际等效蠕变曲线较难获得，为了提高计算效率，本文基于等效线性原则(直线OC)将Δε均匀分解到循环累积应变的各点即可以得到图8(b)中2号线闭合滞回圈(点划线)。

修正前后的动模量计算式如下：

修正前为

( 1 )

按等效线性原则修正后为

( 2 )

按照实际的等效蠕变曲线(OABC)修正后为

( 3 )

二者差异可以表示为

( 4 )

式中：δ为采用两种等效方法得到的动模量的差异。

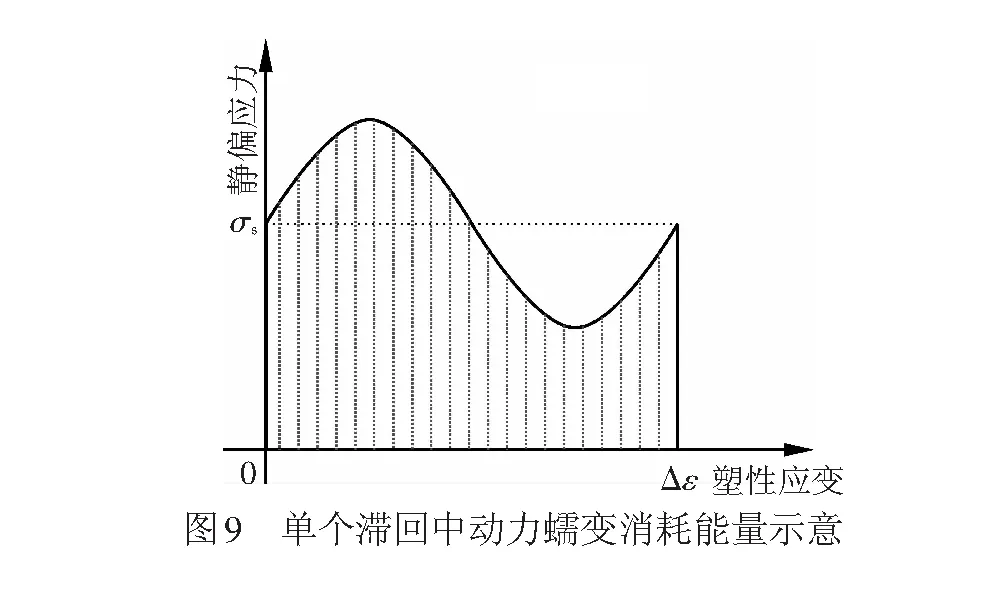
在某一个循环内部，图8(a)中A、B两点在时间轴上大致关于中轴对称，结合等效蠕变曲线可以判断，直线AB应大致平行于直线OC，δ的值为一个接近0的小值。因此可以认为，采用等效线性原则得到的修正动模量与采用实际等效蠕变曲线得到的修正动模量误差较小。在此基础之上，对比可以看出闭合之后的滞回圈变得较为紧凑，即消耗的能量相对未闭合时变少了，差值部分可看做土体蠕变消耗的能量。当采用等效线性原则修正时(即塑性应变随加载过程匀速发展)，通过偏应力与应变的积分易知，蠕变消耗的能量为静偏应力与塑性应变的乘积，见图9。

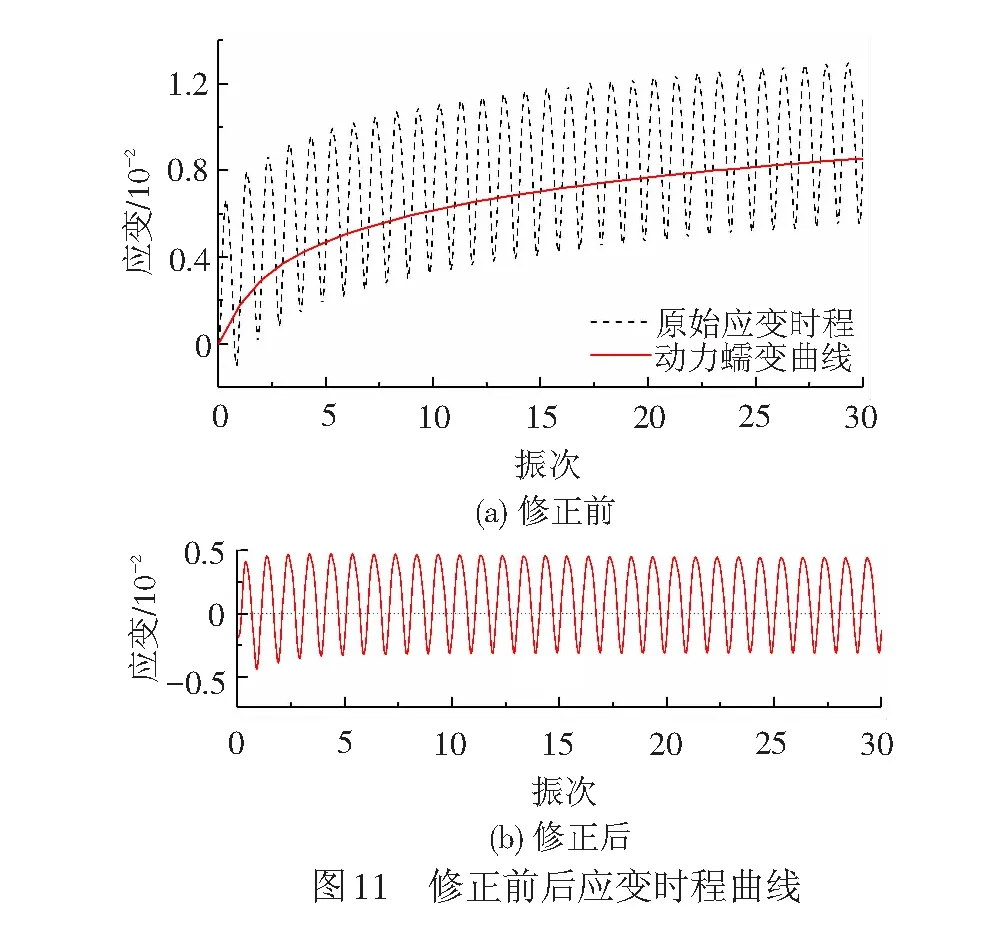
以静偏应力240 kPa、动应力幅值320 kPa工况为例，修正前后的滞回圈和应变时程曲线见图10、图11,图10中虚线为原始滞回圈，实线为修正滞回圈。可以看出，在动力加载初期，塑性变形快速发展，滞回圈严重不闭合。修正之后得到的闭合滞回圈的加卸载段形状没有明显改变，表明本文修正方法没有改变土体的滞后特性[29]。与此同时，本文方法可以很好地将动力蠕变和弹性应变分离开，有助于为交通荷载作用下路基的动力响应和长期变形分析提供更为清晰的研究思路和意义明确的力学参数。

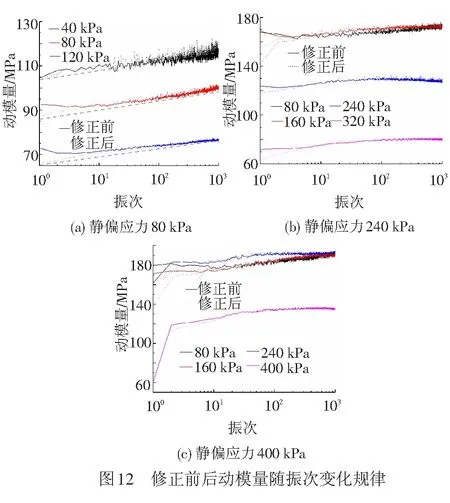
通过对比图12中修正前后动模量随振次的变化规律可以看出：修正对动模量的影响主要体现在加载的前几十个振次，之后由于塑性应变发展速率的减缓，修正对动模量的影响逐渐减弱。从修正后的曲线发展规律可以看出：此时静偏应力对土体动模量的强化作用更加明显。当静偏应力较小时(80 kPa)，在半对数坐标里动模量随着振次近似呈线性增加。