基于SD-GM理论的城市交通拥堵收费模型研究

贾书伟， 严广乐

(1.河南农业大学 信息与管理科学学院，河南 郑州 450002； 2.上海理工大学 管理学院，上海 200093)

0 引言

近年来，因居民生活水平的提高，机动车保有量也在不断攀升，而交通拥堵及机动车尾气污染问题已经变得越来越严重。这不仅仅影响交通安全和出行者的正常出行，而且会导致空气污染。因此，城市交通拥堵成为一个热点话题，并在许多地区中是一项迫切需要解决的任务，如北京，上海，广州和深圳等城市。

针对以上问题，国内外许多学者采用不同的方法进行了大量的研究，也取得了一些有价值的成果。

在交通拥堵问题的研究方面，文献[1,2]研究了城市动态网络车辆路径优化问题和突发事故下交通拥堵的控制策略，在一定程度上缓解了城市交通拥堵。文献[3]研究了城市交通的发生强度与城市规模之间的关系，得出：一旦城市规模的发展超出一定极限，必然会产生难于解决的交通拥堵问题的结论。

在拥堵收费政策的研究方面，英国学者Walters研究了拥堵收费的定价问题，并利用边际效应规律构建了静态模型[4]，实现了社会收益的最大化。近年来，部分学者对静态模型实施改进，研究了动态拥堵收费的定价问题[5,6]，并制定出相应的政策方案。

在实证研究方面, 具有代表性的城市有伦敦[7]，新加坡[8]，瑞典的斯德哥尔摩[9,10]和哥德堡[11]，研究结果表明：拥堵收费政策的实施，能够在一定程度上缓解城市中心区域的交通拥堵程度。

在大气污染方面，也有学者研究了机动车尾气排放[12]和空气质量[13]等问题，因为拥堵会加重机动车污染物排放量。另外，文献[14,15]利用最优化理论来进行动态拥堵定价问题的研究，文献[16]通过对某高速公路维护管理系统的仿真分析，展示了系统动力学方法在交通系统研究方面的有效性和实用性。

然而，很少有学者能够综合考虑到社会，经济及环境等多方面因素对城市交通拥堵和机动车污染物排放的影响，为此，与以往研究不同，本文利用系统动力学与灰色系统理论相结合的方法构建了城市交通拥堵收费管理模型，并利用收费这一经济手段来动态地分析拥堵的成因及缓解策略。以北京市为例，通过对模型中主要变量的仿真和灵敏性分析来确定北京市交通拥堵收费的一种较为合理的范围，进而为治理城市交通拥堵和抑制“雾霾”污染提供政策建议。

1 基于系统动力学的交通拥堵收费管理模型

1.1 系统动力学方法

系统动力学综合利用信息论、控制论、系统论、计算机仿真等理论方法。通过面向系统结构及流程的建模、设计与仿真，定量地模拟不同策略下系统的行为模式，特别适合处理变量间关系复杂，且非线性的情况。其应用十分广泛，如文献[17]引入动态惩罚和补偿策略，并运用系统动力学方法构建地方政府和制造企业之间的混合策略演化博弈模，为我国碳排放减排政策的制定提供了理论依据.文献[18]构建了基于采纳者决策过程的创新扩散系统动力学模型，该研究结果对制定创新推广策略具有一定的指导意义。文献[19]服务型制造项目实施过程中博弈参与主体。分析了三方演化稳定情况，构建了演化博弈模型，利用系统动力学研究了核心制造商、顾客和服务商之间策略选择的动态博弈过程得到了服务商单方面的努力不一定会增加顾客参与的期望收益等结论。文献[20,21]利用系统动力学方法构建了因果回路图和流图，以上研究方法为城市交通拥堵问题的动态仿真分析提供了有效借鉴。

1.2 因果回路图

回路1交通拥堵程度→政府治堵压力→机动车出行成本→机动车出行吸引度→机动车增长率→机动车总量→机动车出行量→车均道路面积→交通拥堵程度。

回路2交通拥堵程度→政府治堵压力→机动车出行成本→改善公共交通的投资和补贴→公共交通供给水平机→动车出行吸引度→机动车增长率→机动车总量→机动车出行量→车均道路面积→交通拥堵程度。

回路3车均道路面积→交通拥堵程度→机动车出行吸引度→机动车增长率→机动车总量→机动车出行量→车均道路面积。

回路4NOx排放量→空气污染→污染治理力度→机动车增长率→机动车总量→机动车出行量→NOx排放量。

回路5机动车出行量→NOx排放量→空气污染→污染治理力度→改善公共交通的投资和补贴→公共交通供给水平→机动车出行吸引度→机动车增长率→机动车总量→机动车出行量。

图中“+”号表示箭头两端变量的变化处于同一方向，“-”号表示箭头一端变量的变化，另一端的变量则会出现相反方向的变化。负反馈是指回路中任何一个初始参数的增加(或减少)都会通过回路中一系列参数的作用后引起这一初始参数的降低(或增加)，相反，正反馈则起自我增强作用。

回路1是一个负反馈回路，最初的交通拥堵程度的增加将会导致政府治堵压力增大，从而会提高机动车出行成本(本文主要考虑拥堵收费政策)，而出行成本的增加，又会降低机动车出行吸引度，较低的机动车出行吸引度会引起机动车增长率的降低，较低的机动车增长率能够降低机动车总量，进而减少机动车出行量，因此车均道路面积将增大，最终会降低交通拥堵程度。即:最初的交通拥堵程度，通过该回路一系列政策措施的作用后，最终的交通拥堵程度将降低。类似地，可分析其它回路。

图1 交通拥堵收费模型的因果回路图

回路2也是一个负反馈回路，即：利用拥堵收费来提高机动车出行成本，又利用改善公共交通的投资和补贴来共同治理拥堵，进而降低对小汽车的依赖，缓解了城市拥堵程度。由回路3可知：最初的车均道路面积通过该回路的作用之后，最终的车均道路面积将减少，从而又恢复了拥堵。因此，仅仅依靠修路来治理交通拥堵只是短暂的，不能从根本上解决问题，必须综合考虑其它政策，如回路2中的拥堵收费政策以及改善公共交通的投资和补贴等政策。

回路4和5分别采用“污染治理”和“改善公共交通的投资和补贴”来治理交通拥堵，借助拥堵收费的经济手段来实现。从而最终降低机动车出行量和NOx排放的增长速度，这不但在一定程度上缓解了城市交通拥堵，而且减少了空气污染，降低PM2.5含量，对“雾霾”程度的加剧具有一定的抑制作用。

1.3 系统模型的构建

根据图1，利用系统动力学软件Vensim绘制相应的流图，见图2。因影响城市交通拥堵系统的因素众多，根据系统动力学建模的几个原则，本文主要关注影响城市交通拥堵的关键变量，从治堵和空气污染减排的角度，提出以下假设。

假设1社会子系统中主要考虑人口总量的变化。

假设2城市人口只考虑常住人口总量。

假设3机动车尾气排放主要考虑NOx排放量，以NOx的污染程度来近似地描述空气污染程度。

假设4资源子系统主要考虑城市土地资源、车均道路面积。

设置：Initial time=2009, Final time=2025, Time step=0.5, Unit of time: Year.

2 参数的确定方法

本文以北京为例，模型中参数的确定方法大致分为以下几类：官网数据，借鉴现有研究文献，估算法，对于具有非线性特征的变量及方程可利用SD-GM理论来构建表函数及逻辑函数。

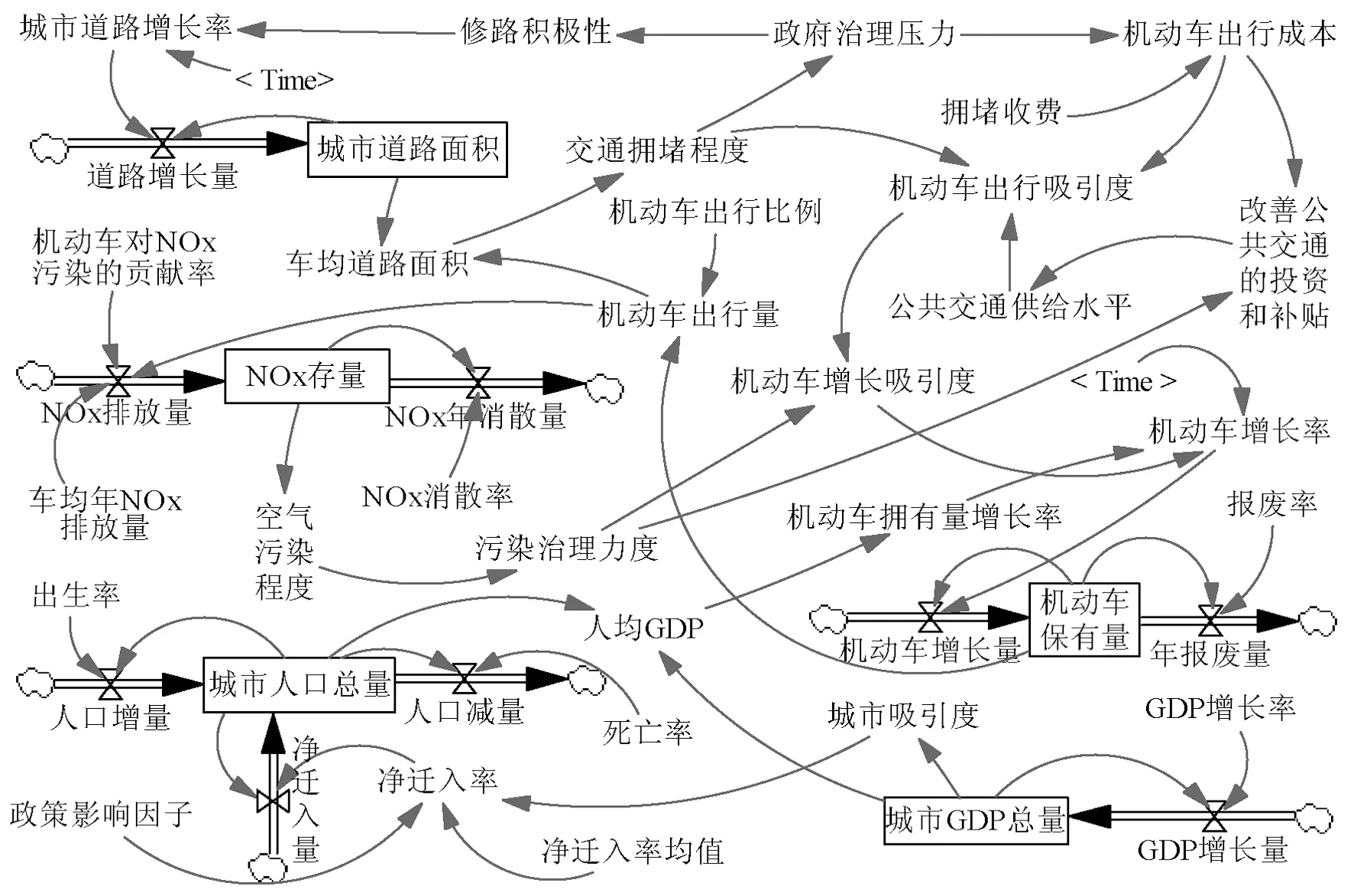
图2 拥堵收费管理模型的流图

2.1 官网数据

通过查阅官方网站的数据，如：《北京统计年鉴2015》，以此来确定部分参数的取值。

(a)北京市城市道路面积(2009～2014年)分别为：9.179e+007m2、9.3956e+007m2、9.164e+007m2、9.236e+007m2、9.611e+007m2和1.0002e+008m2，因此，城市道路面积初值=9.179e+007m2，年均增长率≈0.0173。同理可得：北京市机动车保有量初值=4.019e+006辆；北京市人口总量初值=1.86e+007人(常住人口)；北京市GDP总量初值=1.2153e+012元，GDP年均增长率≈0.1191。

(b)人口出生率(2009～2014年)分别为：7.66‰、7.27‰、8.29‰、9.05‰、8.93‰和9.75‰，故：年均出生率≈8.49‰=0.00849。同理，死亡率≈4.44‰=0.0044。

2.2 现有文献

根据文献[21]可知：(a)年均NOx排放量=0.02吨/年/辆；(b)机动车车对NOx污染的贡献率=0.5；(c)消散率=0.2； (d)报废率=0.067。

根据文献[22]和北京市的实情，机动车出行比例大约是0.55。

2.3 估算值

(a)NOx存量初值≈0.02×401.9×104=80380吨。

(b)城市吸引度的估计值

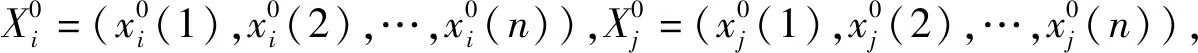
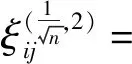
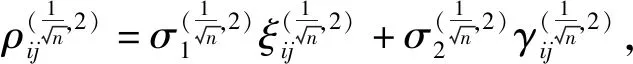
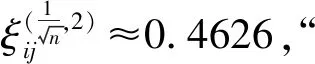
(c)净迁入率的估计

北京市常住人口机械增加值(2009～2014年)分别为：112163人、109091人、129313人、107072人、109656人和74654人，则它们的净迁入率分别为6.03‰、5.56‰、6.41‰、5.17‰、5.19‰和3.47‰，受北京市户口迁入政策的影响，呈现不断下降的规律。而净迁入率均值=5.31‰，远大于3.47‰，与北京户口迁入政策不符合，因此需要调整。本文设置：净迁入率=净迁入率均值×城市吸引度，其中α=1.5。

2.4 基于SD原理的表函数及逻辑函数的构建

因交通拥堵程度，空气污染程度以及公共交通供给水平等都是非线性的，很难直接建立方程，此时可先计算出北京市近10年的车均道路面积和NOx存量，并结合实际拥堵和污染程度来作估计，然后再采用系统动力学软件中的表函数以及逻辑函数等来描述这些非线性关系。

3 动态仿真和分析

3.1 模型测试和仿真

31.1 现实性测试

由图3a可知：(1)当拥堵收费=1000元/天*辆时，机动车排放的NOx总量值最小，当拥堵收费=2元/天*辆时，值最大，该结果与现实情况相符合。(2)曲线1和2的间距最大，说明拥堵收费在2与50元/天*辆之间变化时，所产生的效果最明显，在区间[50,100]内变化较缓慢，超过100，几乎无变化，图3b的分析与之类似。

因此可见，拥堵收费应不超过100元/天*辆，进一步分析见图4。

图3 现实性测试。 (a)NOx存量；(b)通拥堵程度

3.1.2 灵敏性分析

图4a表明：(1)从横向来看，随时间的推移，曲线1虽然增速有所下降，但NOx存量仍在持续上升，因此，拥堵收费为2元/天*辆时，达不到NOx减排的效果。而其它曲线都是先上升后缓慢下降，说明政策实施一段时间后，能够使NOx存量逐年下降，从而达到减排的目的。(2)从纵向来看，随着拥堵收费的增长，NOx存量在不断下降且曲线间距逐渐缩小，其中，区间[2，15]内曲线变化最显著，区间[15，25]内变化较显著，区间[25，35]和区间[35，45]内变化较为缓慢，而超过45元/天*辆，曲线几乎重合，因此，拥堵收费应不超过45元/天*辆。

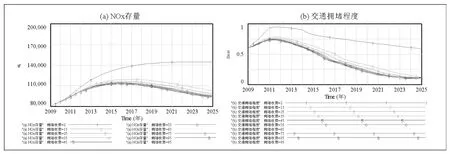
图4 灵敏性分析。 (a)NOx存量； (b)交通拥堵程度

图4b的分析与之类似，即：曲线1也达不到治堵的效果，而从其它曲线的变化中，能够粗略地观察到当拥堵收费在区间[15,45]内变化时，在一定程度上能够缓解交通拥堵程度，只是缓解的程度有所不同。更详细的分析见表1。

表1表明：随着拥堵收费的增长， NOx存量在不断地下降。特别的，区间[2,10]内变化最明显，变化率大约为-25.29%，在区间[10,15]，[15,20]和[20,25]内变化较明显，变化率分别为-4.86%，-2.64%，-1.69%。而在区间[25,30]，[30,35]，[35,40]和[40,45]内变化比较缓慢，分别下降了大约1.01%，0.84%，0.81%和0.76%。这些结果还揭示了：随拥堵收费的增长，虽然NOx存量下降幅度在减小，但总量却在持续不断地下降，并且在区间[25,45]内边际递减效果达到了“相对最小化”。而超过45，几乎无变化，说明并非拥堵收费越高越好。因此，从NOx减排(降低“雾霾”污染)的角度来看，拥堵收费的合理范围应该为[25,45]。

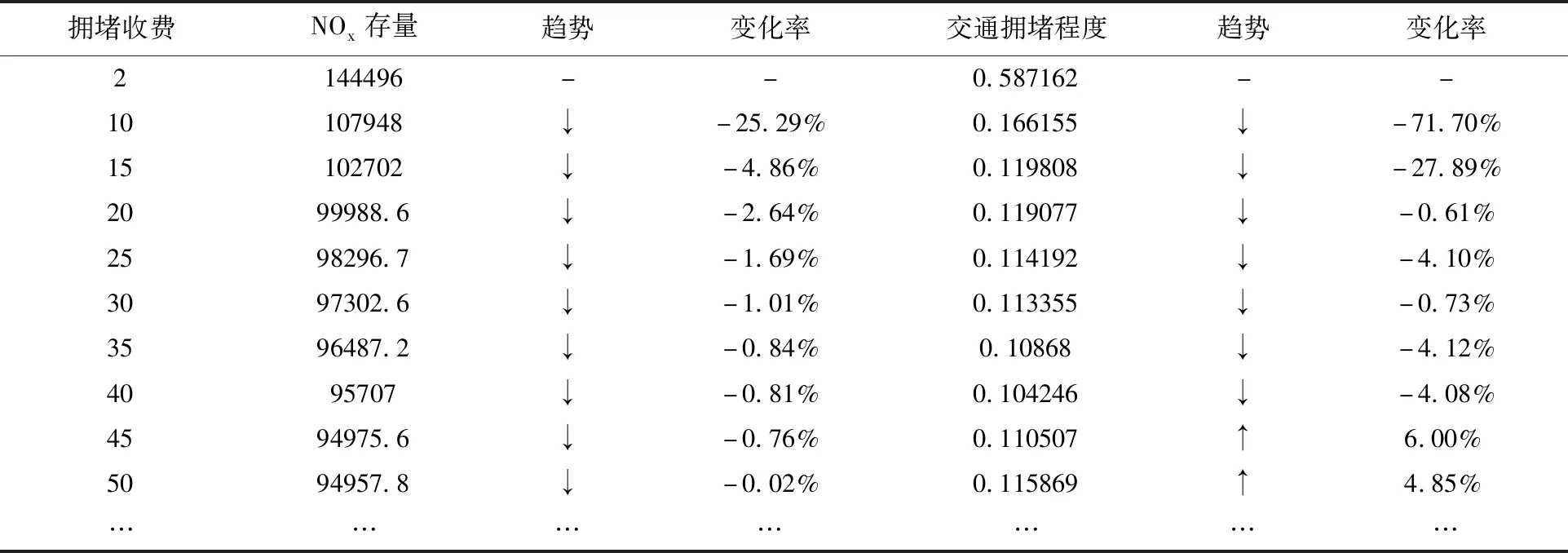
表1 不同拥堵收费对NOx存量和交通拥堵程度的影响(2025年)

类似地，随着拥堵收费的不断增长，在区间[2,10]和[10,15]内，交通拥堵程度有了显著下降，变化率分别是-71.70%和-27.89%。而拥堵收费在20至40元/天*辆之间增长时，交通拥堵程度的下降速度比较缓慢，分别下降了大约4.10%，0.73%，4.12%，4.08%。但超过40，会产生相反的效果，例如，当拥堵收费为45元/天*辆时，交通拥堵程度为0.110507，虽然低于收费为2元/天*辆时的0.587162，但高于0.104246(当拥堵收费为40元/天*辆)。因此，从交通拥堵程度的下降效果来考虑，拥堵收费应不超过40元/天*辆，即在区间[20，40]内将会达到较为有效的治堵效果。

综上所述，从NOx减排和治堵效果的角度来综合考虑，拥堵收费的较合理范围为[25,40]。

图5 主要变量的敏感性测试。(a)NOx存量；(b)交通拥堵程度；(c)机动车出行量； (d)车均道路面积

3.1.3 敏感性测试和分析

区间[25,40]进行等分，步长为1，进行敏感性趋势分析。图5a～5d表明：因参数的不同，仿真结果也略有差异，但图形变化趋势基本相同，没有出现过于敏感或过于不敏感的地方。

从图5a中可以清晰观察到：NOx存量的大致趋势是先缓慢上升，持续一段时间后会逐渐下降。具体地，在拥堵收费政策实施前期(2015年之前)，减排效果并不十分明显，NOx存量仍在不断增加，原因可能是：因受出行者出行习惯的影响，加之部分出行者对“雾霾”污染和交通拥堵的成因及危害性等认识不足，从而在政策实施前期，并没能很好地降低NOx存量。因此，建议：在政策实施前期，应加大对“雾霾”和交通拥堵的危害性的宣传力度。在仿真模拟的中期(2015～2017年左右)，NOx存量基本上呈现“水平直线型”变化态势，说明随着政策的不断实施与完善，NOx存量的上升趋势得到了有效控制。从图5a中还可以观察到：大约从2018年之后，NOx存量将会逐年下降，从而使“雾霾”污染能够在一定程度上得到缓解。

相应地，图5b表明：虽然在初期，交通拥堵程度仍有所上升，但拥堵收费政策实施一段时间之后，会稳步下降。类似地，图5c和5d显示：机动车出行总量在得到有效控制的基础上有所下降，而车均道路面积也有了一定程度的上升。

另外，图5a～5d还能观察到NOx存量，交通拥堵程度和机动车出行量的下降速度比较缓慢，而车均道路面积上升的程度也很有限，这些结果共同揭示了：仅凭拥堵收费政策并不能在短期内从根本上彻底消除交通拥堵或“雾霾”，而只是在某种程度上能够缓解拥堵或抑制“雾霾”污染。

3.2 模型检验

本节以北京市GDP总量为例，分别进行均方差比和小误差概率合格检验，其它变量的检验与之类似。

分别为序列X(0)的均值和方差，称

分别为残差的均值和方差。

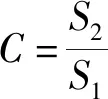
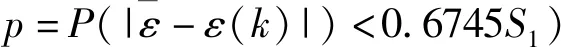
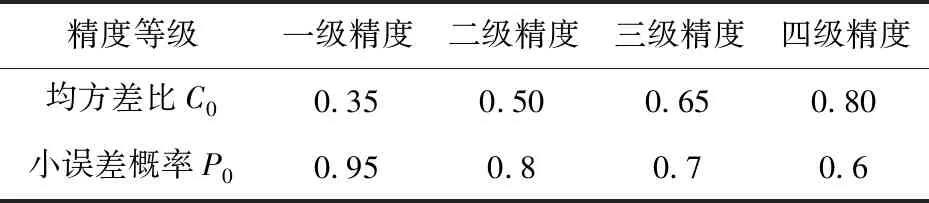
表2 精度检验等级参照表[24]

北京市GDP总量的真实值序列及其仿真值序列分别记为

则原始数据序列的均值与方差分别为

残差的均值和方差分别为

因此，∃C0=0.35，使得

所以：根据定义2和表2可知均方差比精度为一级。

计算小误差概率：

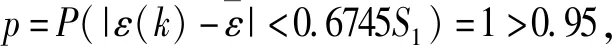
3.3 政策分析

拥堵收费以40元/天*辆为例，与基本情况(2元/天*辆)相比，比较结果见图6a～6d和表2。

表2显示：当拥堵收费=40元/天*辆时，与基本情况(2元/天*辆)相比， 交通拥堵程度， NOx存量，机动车出行量和机动车出行吸引度分别下降了82.25%、33.76%、39.64%和43.26%；而车均道路面积却增加了大约65.68%，这些结果说明：当拥堵收费=40元/天*辆时，不但能够有效缓解交通拥堵，而且能够降低机动车尾气排放，从而在一定程度上减少大气污染，抑制“雾霾”污染程度的加剧。

详细地，图6a表明，曲线2是先增后减，大约从2017年开始，持续下降，并且在2025年下降了大约33.76% (与曲线1相比)，NOx减排效果比较明显.在图6b中，曲线2与曲线1相比，下降速度更显著，而且能够提前实现缓堵的目的。图6c的变化规律与图6b相似。相反，图6d则是先缓慢下降而后逐年上升，从而能够进一步缓解道路拥堵。

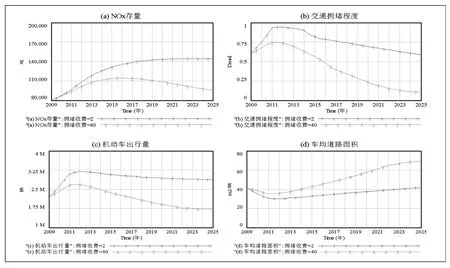
图6 不同拥堵费对主要变量的影响。(a)NOx存量；(b)交通拥堵程度；(c)机动车出行量；(d)车均道路面积

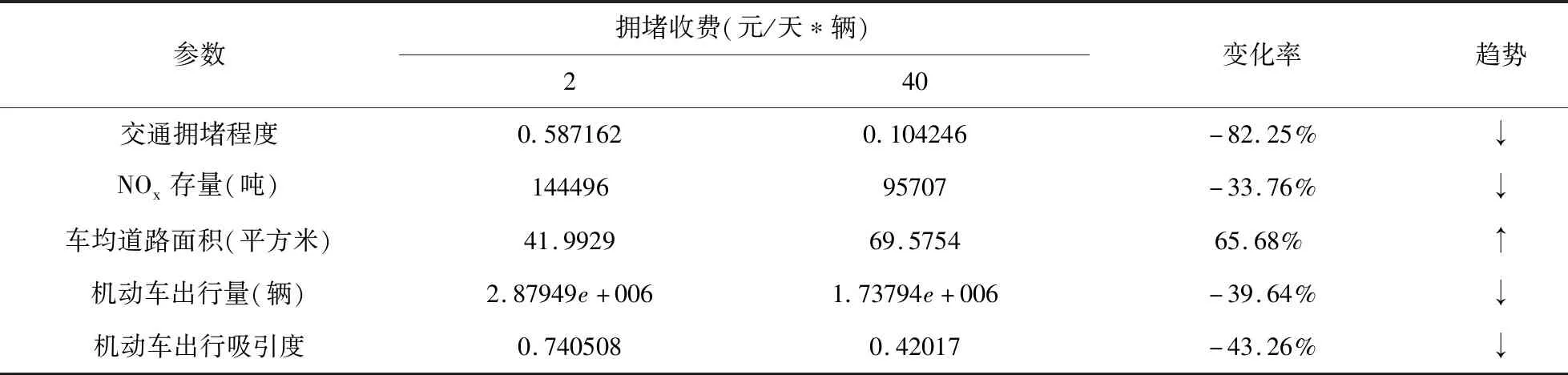
表3 不同交通拥堵收费的比较(2025年)

4 结论

为了缓解北京市交通拥堵及其引起的“雾霾”污染，本文利用系统动力学方法，构建了一种拥堵收费模型，通过因果回路分析了北京市交通拥堵产生的原因，并找出影响交通拥堵的关键变量。进而采用拥堵收费政策来进行仿真和灵敏性分析，计算出不同拥堵收费政策下各关键变量的变化程度，得到以下结论：在一定范围内，随着拥堵收费的增加，NOx存量，机动车出行吸引度，机动车出行量和交通拥堵程度都有所下降，而车均道路面积有了一定程度的上升;但并非拥堵收费越高越好，在区间[25，40]内，拥堵收费的增长所产生的治堵和NOx减排效果将达到“相对最大化”。因此，25至40元/天*辆是北京市交通拥堵收费的一个较为合理的范围。

然而，因数据有限，本模型仍然存在一些局限。例如，本文通过仿真和灵敏性分析，只是粗略的估计出适合北京市交通拥堵收费的大致范围，并没有精确地确定其准确范围。另外，该模型主要考虑了机动车总量，没有细分到各类不同排量的机动车;在提高机动车出行成本中主要考虑交通拥堵收费，没有考虑如提高停车费以及燃油税等其它因素;另外，虽然拥堵收费政策能够有效缓解拥堵和降低大气污染，但因该政策的实施，部分机动车出行者会转向公共交通，从而会加重公共交通负担，因此，又有必要采取补贴等政策来提升公共交通供给水平，将多政策进行综合集成，收费和补贴等政策的组合模型将更有利于城市交通拥堵的治理，这些都是今后研究中需要不断完善的地方。