基于堆积试验的黏壤土仿真物理参数标定

向 伟，吴明亮，吕江南，全 伟，马 兰，刘佳杰

基于堆积试验的黏壤土仿真物理参数标定

向 伟1,2，吴明亮1※，吕江南2，全 伟1，马 兰2，刘佳杰2

（1. 湖南农业大学工学院，长沙 410128；2. 中国农业科学院麻类研究所，长沙 410205）

为获取南方黏壤土的离散元仿真模型精准接触参数，构建土壤离散元仿真模型，基于土壤堆积试验，结合试验测定和EDEM软件推荐的参数构建土壤仿真模型，以休止角为响应值，采用Design Expert软件依次设计Plackett-Burman试验、最陡爬坡试验和Box-Behnken试验完成土壤仿真物理参数标定及优化。进一步通过成穴装置成穴的仿真试验与土槽试验的对比分析，验证黏壤土仿真模型的精准性。成穴试验的仿真与土槽试验结果表明，装置在仿真土壤中运动规律与土槽试验中差异较小，成型穴孔的开口纵长和有效深度的误差分别为3.98%和1.87%，模拟仿真土壤的物理力学特性与实际土壤一致，表明黏壤土的离散元仿真参数系统标定研究的方法准确可行。研究构建了南方黏壤土精准的离散元仿真模型，为该类型土壤与触土部件相互作用的动力学研究提供技术支持。

模型；离散元；黏壤土；参数标定；休止角；仿真参数；JKR接触模型

0 引 言

采用实测试验与仿真模拟相结合的方法研究触土机具与土壤相互作用规律，可从细观上研究受机具作用下土壤颗粒的动态行为，直观量化分析土壤在机具作用下的运动规律，为农机具的优化提供技术支持[1-3]。土壤颗粒具有典型的离散性[4]，且与触土部件作用时土壤颗粒呈现动态变化，离散元法分析中将土壤看作由一系列离散的独立运动的颗粒单元组成，整个土壤的运动和变形由各颗粒单元的运动和相互位置来描述，因而选择离散元法进行土壤数值模拟更为精准[5-7]。

构建散粒体的离散元仿真模型，其核心技术为仿真参数的确定，主要包括本征参数和物理参数[8-10]，大部分参数可通过试验测定得出，而部分参数（尤其是物理接触参数）很难通过试验获取，因而许多学者提出采用实测试验结合虚拟标定实现仿真参数的精准标定[11-15]。Coetzee等采用剪切和侧限压缩试验对玉米颗粒的摩擦系数和刚度系数进行标定，并进行了试验验证[16]。Grima等基于崩塌试验中颗粒堆休止角分别对干、湿颗粒在离散元仿真中所需滚动摩擦系数进行了标定[17]。刘凡一等基于堆积试验，采用模拟仿真与响应面法相结合完成小麦离散元仿真参数的标定[18-19]。在土壤离散元仿真模型参数标定研究方面，Ucgul等通过结合Hertze-Mindlin及Hysteretic spring接触模型，完成土壤粘结力及无粘结力土壤仿真参数标定，解决了其受力塑性形变等问题[20-21]。张锐等应用Hertz-Mindlin接触模型，对标准球和非标准球的无黏性沙土颗粒的碰撞恢复系数与摩擦因数进行了标定，建立了沙土接触模型[22]。王宪良等采用EDEM软件外置编译ECM接触模型，以休止角等因素为目标值对砂壤土的颗粒半径和摩擦因素等进行标定，并进行了轮胎-土壤压实接触仿真验证[23]。武涛等基于土壤休止角物理试验结果，采用JKR接触模型借助GEMM数据库获得离散元模型关键参数初始范围，运用Box-Behnken试验方法进行休止角仿真模拟，通过回归分析求取砂壤土仿真模型参数的最优值[24]。

应用离散元法研究散粒体动力学问题已成为一种发展趋势[25-28]。利用离散元法建立土壤仿真模型，本征参数可通过试验实测得出，在离散元软件数据库中，多数土壤颗粒的物理参数的推荐值与真实数值相近，但由于颗粒间接触特性复杂，部分参数需要进行精准标定及优化，在土壤的离散元仿真参数标定研究方面，尤其是砂土及砂壤土等类型土壤的仿真参数标定研究，各国学者已经做了许多的探索[29-30]，针对中国南方地区种植土壤黏壤土的仿真参数系统标定研究却少见报导。本研究采用实测试验与仿真模拟相结合，提出一种显著性分析和响应面法相结合的方法，对中国南方地区黏壤土的离散元仿真参数进行系统的标定研究；通过筛分试验、三轴剪切试验等测定样品土壤的本征物理力学特性参数，基于土壤堆积试验，结合试验测定和EDEM软件的GEMM数据库推荐的参数构建土壤仿真模型，以休止角为响应值，采用Design Expert软件依次设计Plackett-Burman试验、最陡爬坡试验和Box-Behnken试验完成土壤仿真参数标定及优化；进一步通过穴孔成型装置的仿真试验与土槽试验的对比分析，验证黏壤土离散元仿真模型反映土壤物理力学特性的准确性，以期构建中国南方地区种植土壤黏壤土精准的离散元仿真模型。

1 黏壤土本征参数测定

1.1 土壤原型及粒径分布

土壤样品为中国南方种植土壤黏壤土，采自湖南农业大学农业机械化工程实训中心试验土槽，含水率为15.8%，采用比重瓶法测得土壤密度为2 680 kg/m3。如图1所示，采用筛分法测定土壤粒径分布及百分含量，土壤粒径为＞5、5～2.5、2.5～1和＜1 mm的质量和质量分数分别为93.12 g、11.64%，194.96 g、24.38%，343.68 g、42.89%和168.24 g、21.09%。

图1 土壤粒径筛分试验

1.2 土壤直剪试验

采用SJ-1A型应变控制式三轴剪力仪，可测得试验土壤的弹性模量，确定泊松比，进一步分析得出试验土壤的剪切模量[22]。试验过程中加载3种不同围压，每组试验重复4次，分别取平均值记为试验土壤的指标参数，并计算出其标准偏差。

根据试验数据绘制图2所示的主应力差—轴向应变关系曲线图，主应力差与轴向应变的比值，即图中曲线线性变化段的斜率为土壤的弹性模量。

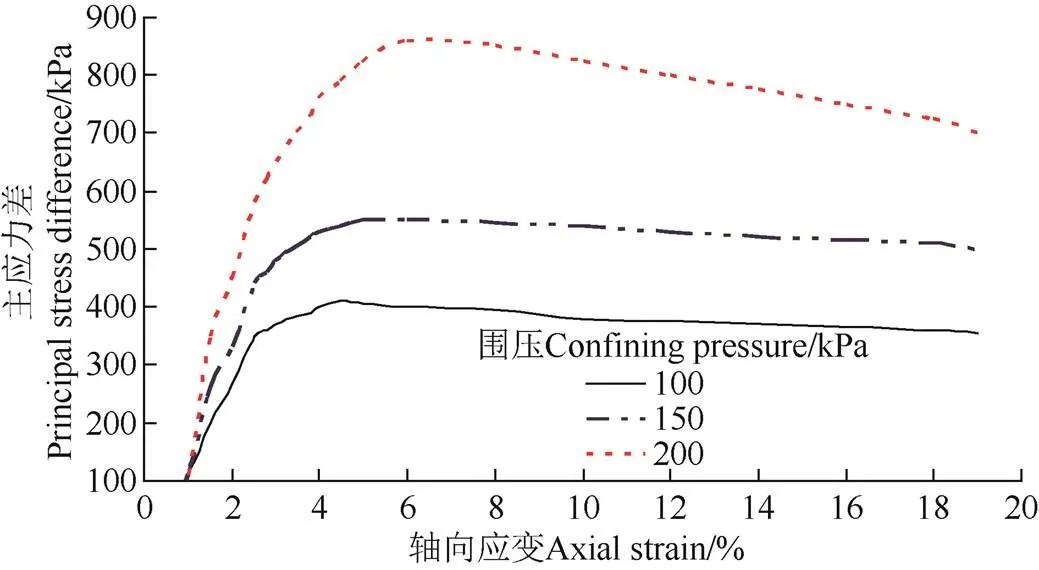
图2 主应力差-轴向应变关系曲线

弹性模量的计算公式为

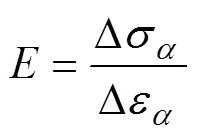
泊松比为土壤本征参数，南方黏壤土的泊松比一般为0.25～0.45，根据样品黏壤土的特性与相关文献，选用泊松比n为0.38[31]。剪切模量的计算公式为

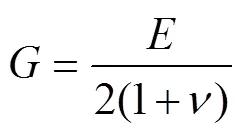
得出试验土壤的剪切模量1.2×103kPa，标准偏差0.099 kPa。

1.3 土壤堆积试验

采用漏斗法测定土壤的休止角，其实测试验装置如图3a所示，主要由三角铁架、漏斗和接土盘组成。试验后，采用Matlab读取土壤堆单侧图像，对图像分别进行去噪、灰度、二值化处理，最终提取图像边界点，对边界点进行线性拟合，得出拟合直线的斜率即为土壤休止角的正切值。

图3b所示为土壤堆积仿真模拟试验装置。仿真模拟试验中，漏斗下端落料口一直处于打开状态，随着仿真土壤颗粒的不断生成，落料口下端一直落料，直至所有土壤颗粒停止运动则模拟结束，采用EDEM软件自带的量角器功能测定土壤休止角。

图3 休止角测定试验装置

土壤堆积实测试验重复4次，取平均值记为试验土壤的休止角，其结果为42.4°，标准偏差0.45°。

2 土壤仿真参数模拟标定

2.1 土壤仿真模型

中国南方地区种植土壤黏壤土具有较强的粘结性和弹塑性，EDEM软件中内置的Hertz-Mindlin with JKR模型（简称JKR模型）能模拟颗粒受力条件下土壤应力-应变特征，该模型不仅能体现颗粒的弹塑性，且能体现颗粒的粘结性[32]，本文采用EDEM 2017版开展仿真模拟试验，选择JKR模型为土壤颗粒接触模型。

堆积试验的离散元仿真模型参数主要为：本征参数和物理参数。

（1）前文已完成土壤本征参数的测取。根据实测的土壤粒径及百分含量测定数值，设定模拟土壤的粒径及质量百分比分别为：5 mm，11.64%；3 mm，24.38%；1 mm，63.98%。土壤堆积仿真试验中，试验装置材料为钢材，其本征参数为：密度7.85×103kg/m3，泊松比0.3，剪切模量7.0×107kPa[22]。

（2）将土壤及钢材的本征参数和仿真规模输入到EDEM软件中，从GEMM数据库获取仿真参数的范围值和推荐数值分别为：土壤-钢材恢复系数0.2～0.5，0.3；土壤-钢材静摩擦因数0.5～1.2，0.6；土壤-钢材滚动摩擦因数0.05～0.2，0.1；土壤泊松比0.25～0.45，0.38；土壤JKR表面能7.5～14.5 J/m2，12.5 J/m2；土壤-土壤恢复系数0.15～0.75，0.6；土壤-土壤静摩擦因数0.44～1.16，0.85；土壤-土壤滚动摩擦因数0.05～0.2，0.1。

2.2 仿真参数标定方法

EDEM软件的GEMM数据库对土壤仿真参数的推荐并非基于土壤不同类型和不同物理特性条件下的精准数值，由于土壤的多样性，导致不同土壤的物理参数差异性较大，因而需基于推荐范围值对试验土壤的仿真参数进行精准标定及优化。

（1）应用Design Expert 软件设计Plackett-Burman试验，以土壤休止角为响应值，筛选出影响显著的物理参数。仿真模拟试验中共8个真实参数1～8，设计3个虚拟参数9～11，每个参数按照推荐范围值均取低、高2个水平，分别以编码−1和+1表示，如表1所示。仿真试验中设定1个中心点，共进行12 组试验，每组仿真模拟试验重复4次，取平均值记为单组试验的休止角。

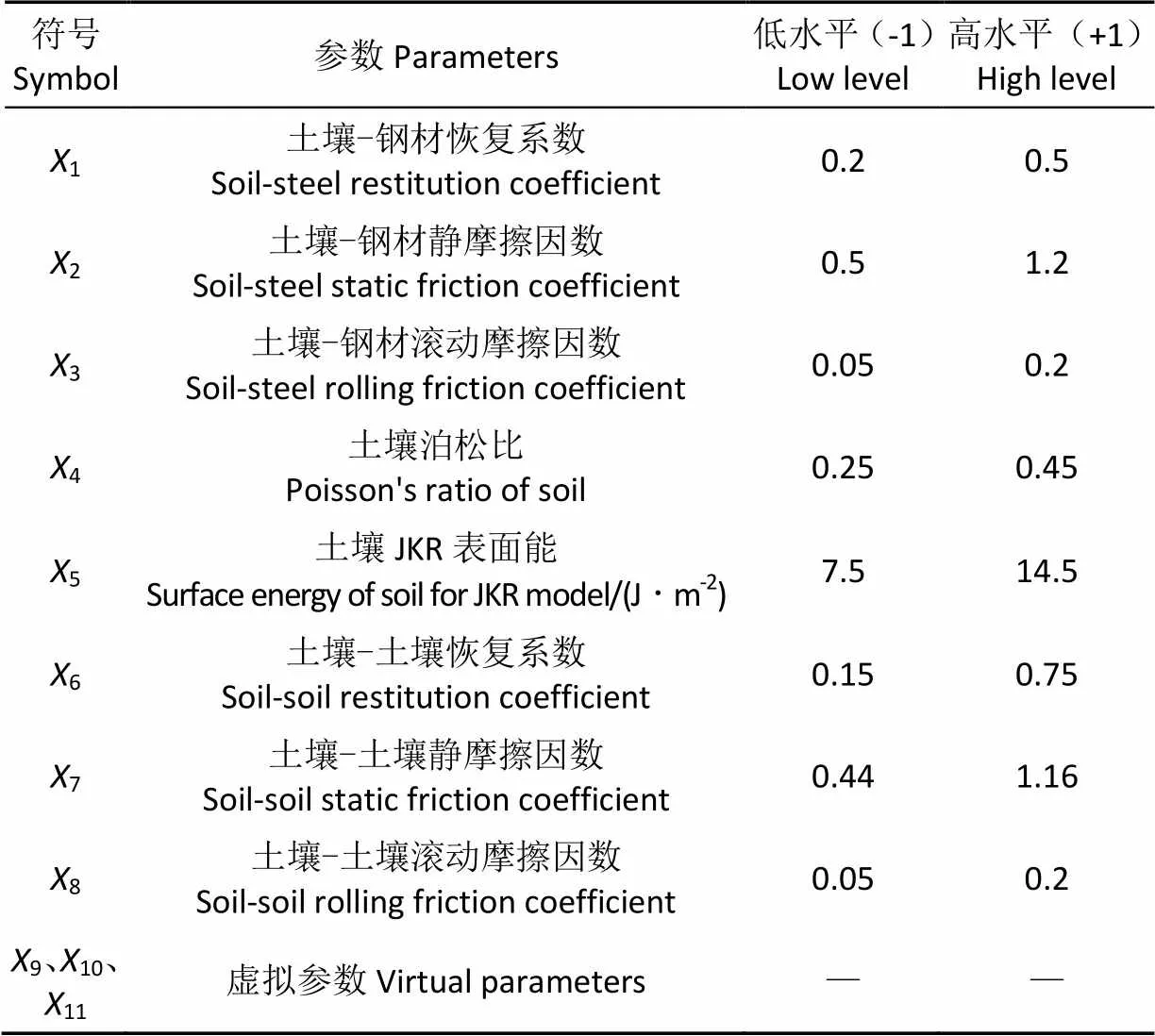
表1 Plackett-Burman 试验参数列表

（2）基于Plackett-Burman 试验筛选出的显著性参数，设计最陡爬坡试验，进一步缩小显著性参数的范围值，以准确地进入到最优值的附近区域。仿真模拟试验时，非显著性参数取GEMM数据库的推荐数值，显著性参数按照设计的步长逐步增加，记录并分析仿真试验的休止角，分别计算仿真试验结果与实测试验结果的相对误差。

（3）基于最陡爬坡试验结果，根据Box-Behnken试验设计，显著性参数取高、中和低3个水平设计试验，分别以编码+1、0和−1形式表示，非显著性参数取值同最陡爬坡试验，记录每组仿真试验的休止角。此外，试验中采用5个中心点进行误差估计，共进行17组试验，每组仿真模拟试验重复4次，取平均值记为单组仿真试验的数值结果。

2.3 结果与分析

2.3.1 Plackett-Burman试验

表2所示为Plackett-Burman试验的设计方案及仿真模拟结果，采用Design Expert软件对该模拟试验结果进行方差分析，得出各参数的影响效果如表3所示。

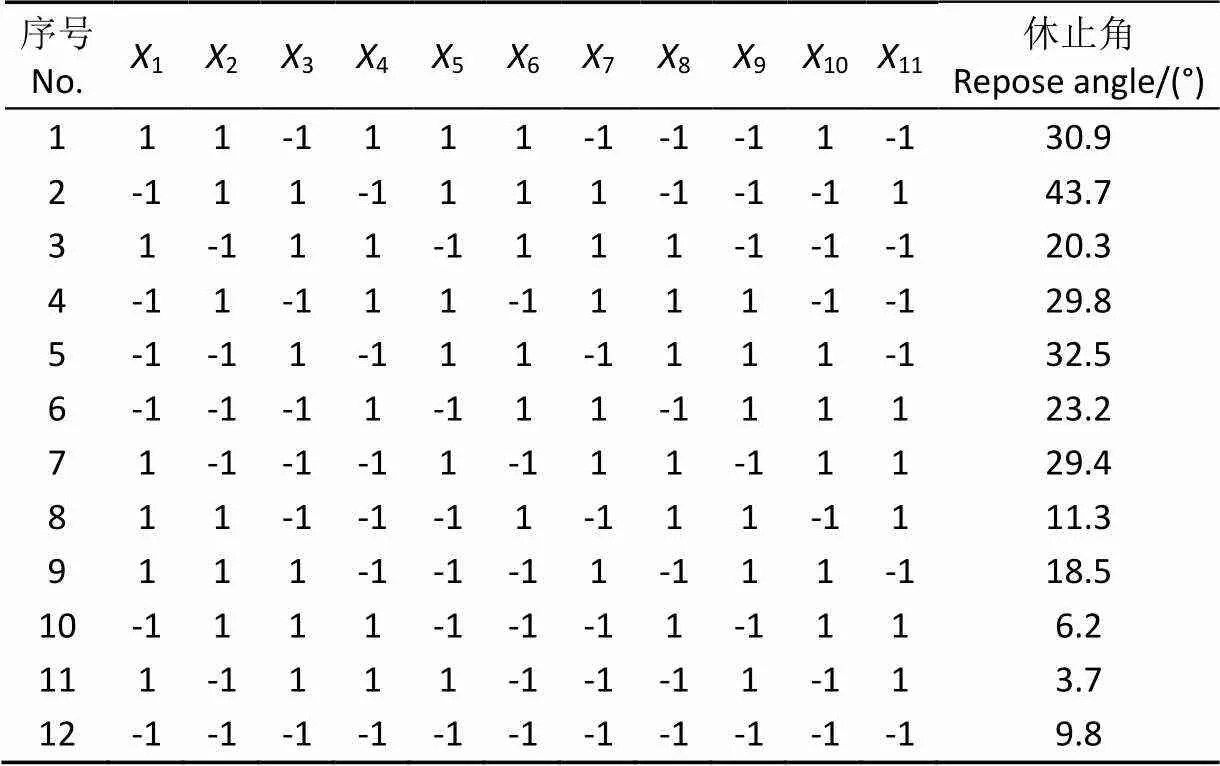
表2 Plackett-Burman 试验方案设计及结果

注：变量1-11含义同表1。

Note: The variables1-11are equal to those in table 1.

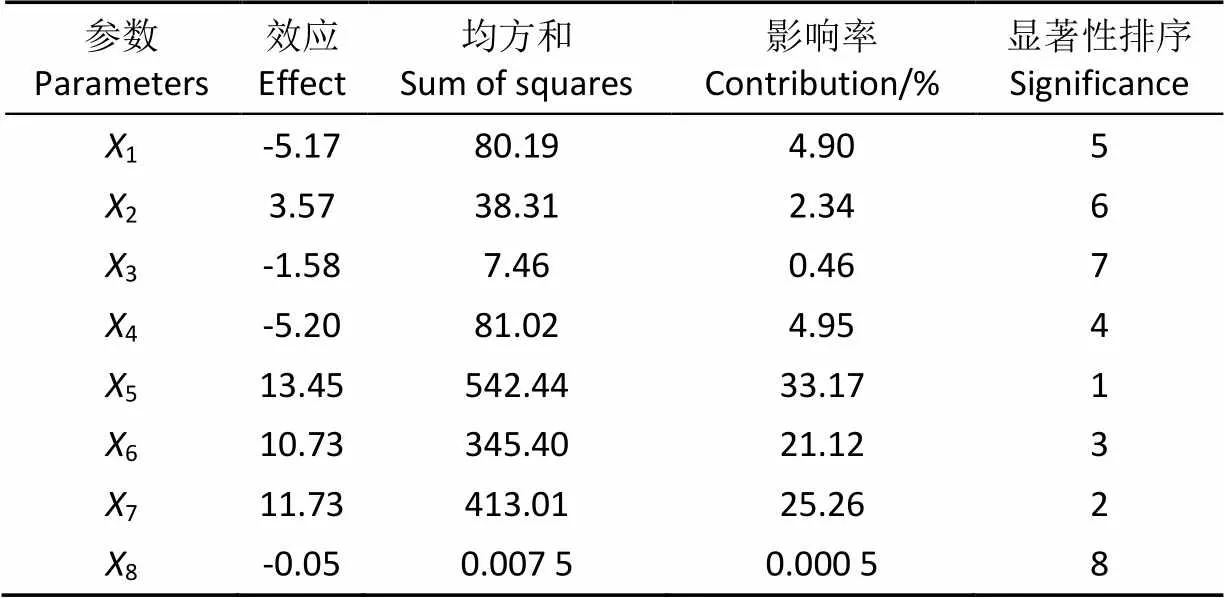
表3 Plackett-Burman 试验参数显著性分析

表3结果显示：仿真参数5—土壤JKR表面能（）、6—土壤-土壤恢复系数（）、7—土壤-土壤静摩擦因数（）对土壤颗粒休止角影响显著，其余参数影响较小，并不显著。因此，在后续的最陡爬坡试验以及Box-Behnken试验中开展、、共3个影响显著的物理参数的标定及优化。

2.3.2 最陡爬坡试验

表4所示为最陡爬坡试验设计方案及结果，结果表明：随着、、数值的增加，仿真试验得出的休止角逐渐增大，而仿真与实测试验得出的土壤颗粒休止角的相对误差呈现先减小后增加的趋势；在4号试验水平时，休止角的相对误差达到最小值，由此可知，试验变量的最优区间在4号试验水平附近。因此，选取4号水平为中心点，设为中水平，选取3号、5号水平分别为低、高水平进行后续的Box-Behnken试验和回归模型分析；物理参数、、的低、中、高水平分别为10.3 J/m2、11.7 J/m2、13.1 J/m2，0.39、0.51、0.63和0.73、0.87、1.02。

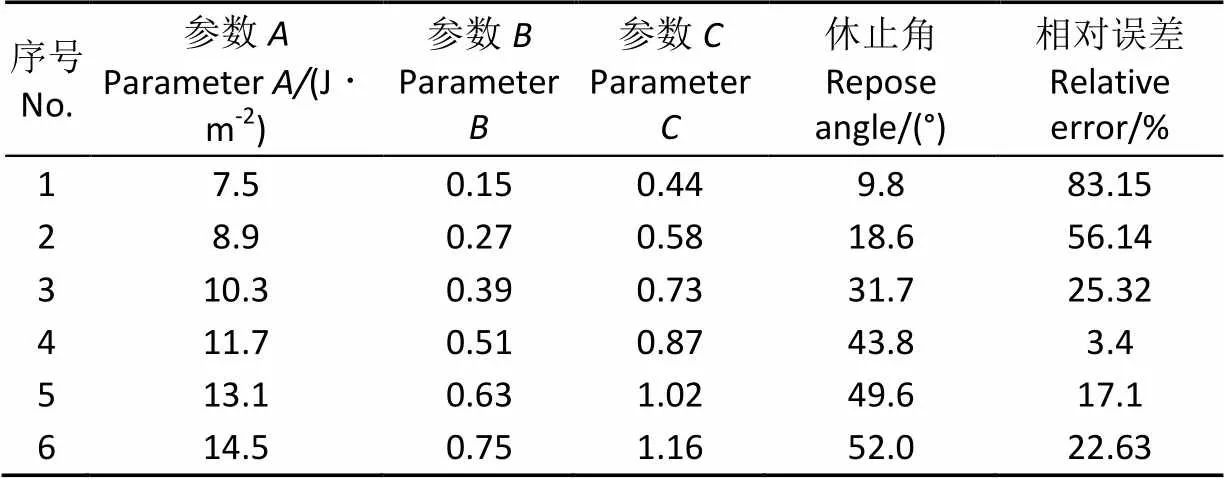
表4 最陡爬坡试验设计方案及结果

注：参数、、指参数5、6、7，下同。

Note: Parameter,andare equal to parameter5,6,7, reopectively. The same below.

2.3.3 Box-Behnken试验和回归模型

表5所示为Box-Behnken 试验设计方案及结果，根据试验结果，采用Design-Expert软件建立土壤颗粒休止角与3个自变量（编码值）的二阶回归模型，其二次多项式方程为

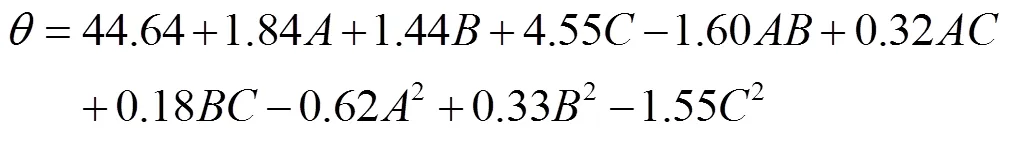
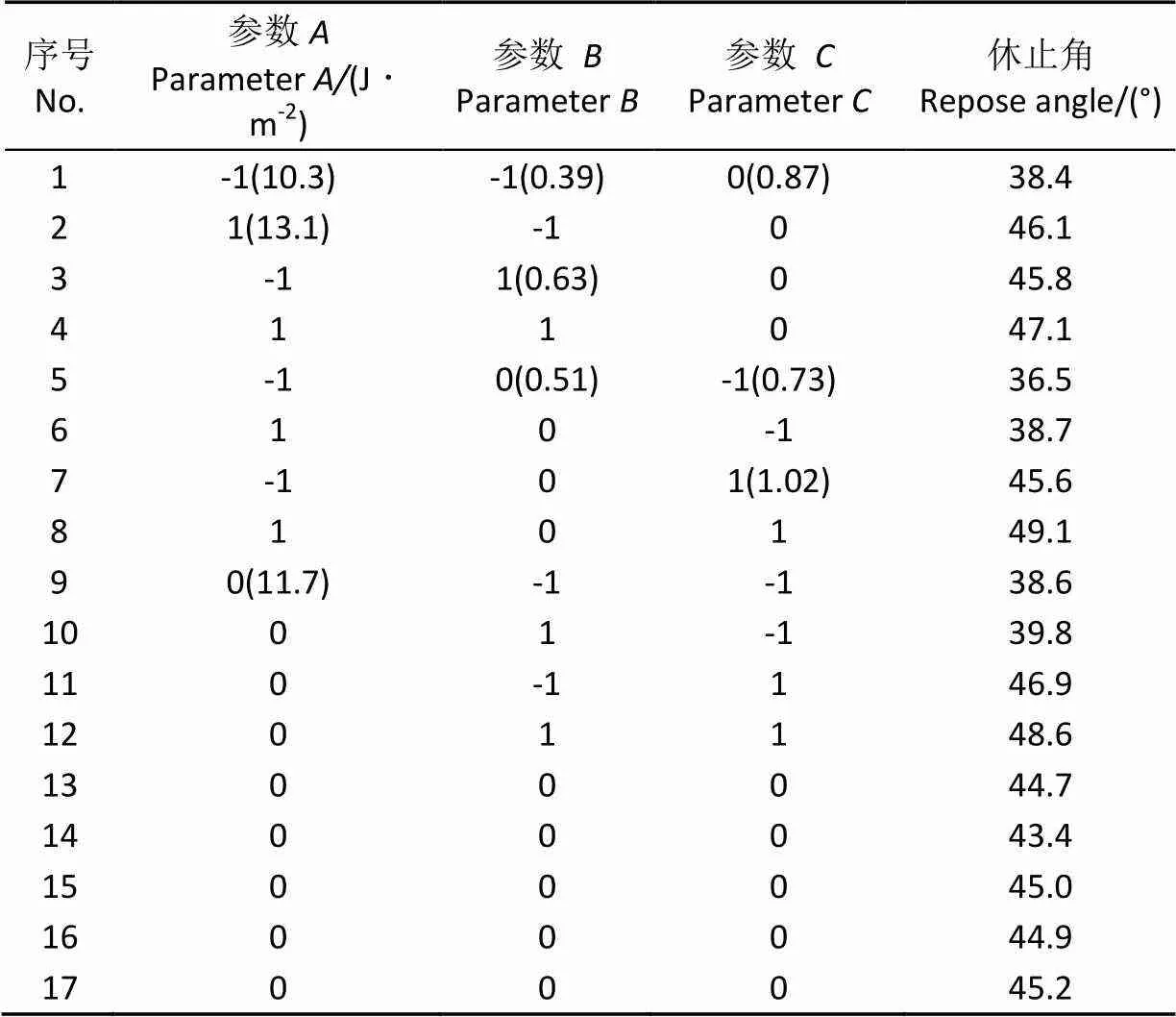
表5 Box-Behnken 试验设计方案及结果

对表5的试验模型进行方差分析，得到结果如表6所示，结果表明：方程模型值为0.000 2，呈现极显著性（<0.01），在统计学上是有意义的，表明该模型因变量（休止角）与所有自变量之间均呈现极显著性；失拟项不显著（=0.118 6>0.05）表明，采用此模型进行结果分析，虽存在一定的失误概率，但该方程的模拟可信；决定系数2=0.967 6、校正决定系数2adj=0.926 0，二者均接近1，表明拟合方程有意义，其可靠度高；变异系数=2.41%、精密度Adeq precision达到16.305，表明该模型具有良好的可信度和精确度。

表6结果表明：模拟的一次项、、对休止角影响极显著，交互作用项和二次项2对休止角影响显著。从单因素水平分析，各因素对休止角的影响顺序：（土壤-土壤静摩擦因数）>（土壤JKR表面能）>（土壤-土壤恢复系数）；交互作用存在下，交互作用项对休止角影响顺序：>>。

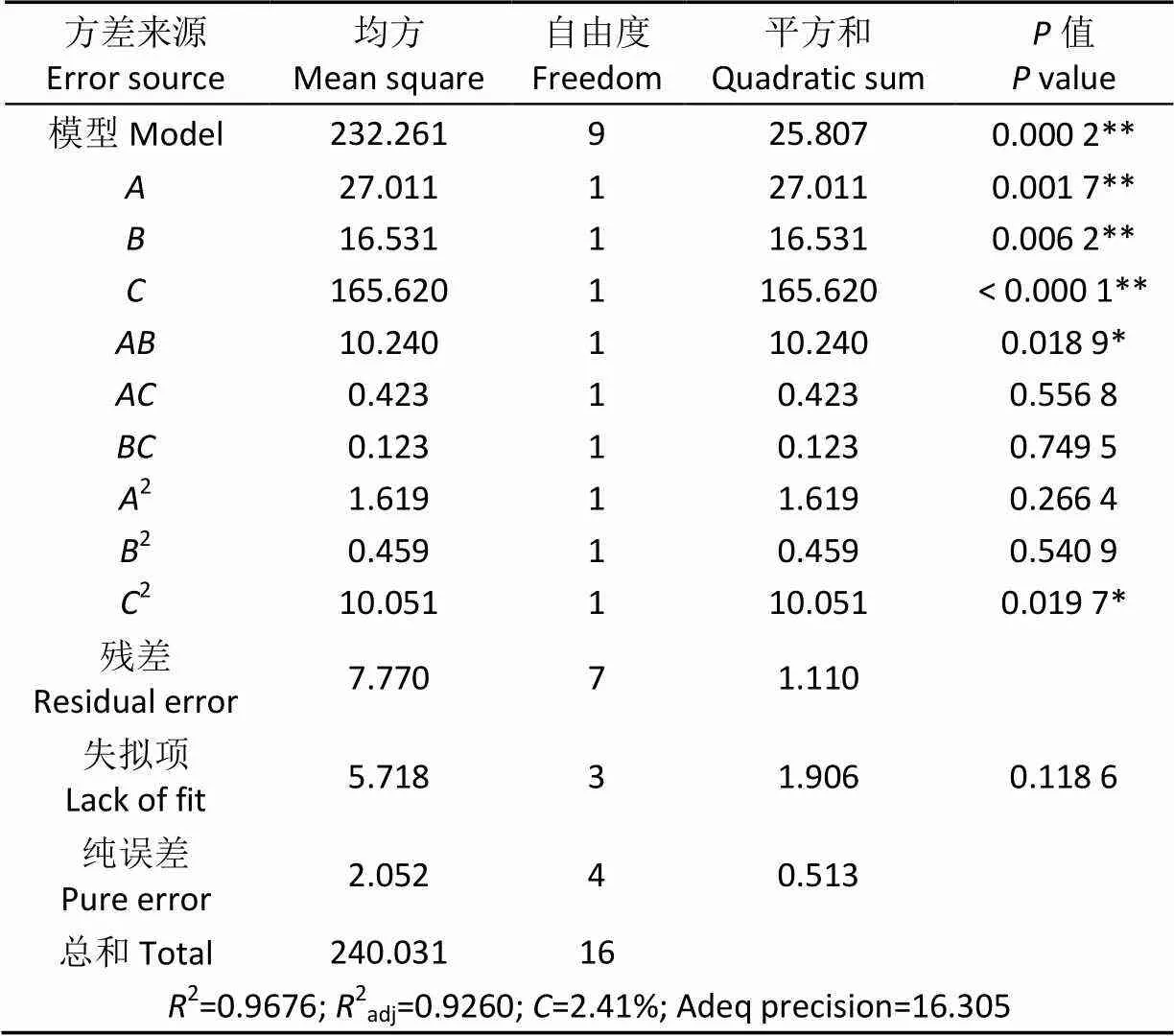
表6 Box-Behnken 试验二次多项式模型方差分析

注：**表示该项极显著(<0.01)，*表示该项显著(<0.05)。

Note: ** and * indicated significance at 0.01 and 0.05 levels, respectively.

2.3.4 回归模型交互效应分析

本试验以土壤休止角作为土壤仿真模型参数标定的评价指标，采用Design Expert软件对模型数据进行二次多元回归拟合，得出图4所示的影响目标函数休止角的参数间相互作用的响应面和等高线分布图，分别为土壤JKR表面能和土壤-土壤恢复系数交互作用、土壤JKR表面能和土壤-土壤静摩擦因数、土壤-土壤恢复系数和土壤-土壤静摩擦因数交互作用。

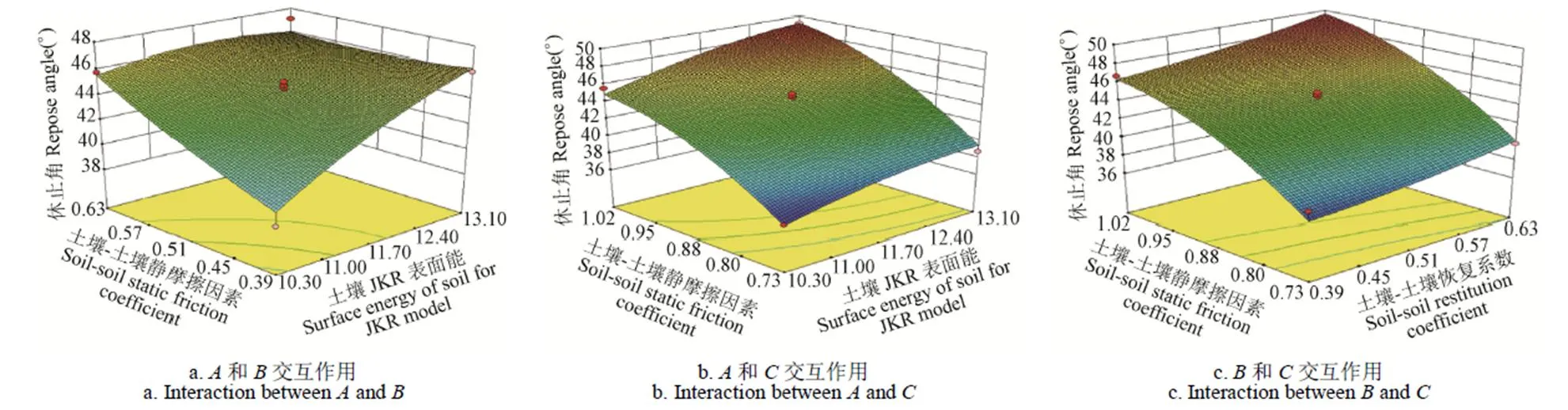
图4 影响休止角的参数间的交互作用

图4a可看出，土壤JKR表面能和土壤-土壤恢复系数变化引起的休止角变化较小，同时等高线呈现较大曲率的椭圆形表明，土壤JKR表面能和土壤-土壤恢复系数交互影响显著；图4b、图4c的响应面的坡度较大，表明土壤JKR表面能和土壤-土壤静摩擦因数、土壤-土壤恢复系数和土壤-土壤静摩擦因数对休止角的影响较大；图4b、图4c的等高线的曲率平缓，表明土壤JKR表面能和土壤-土壤静摩擦因数、土壤-土壤恢复系数和土壤-土壤静摩擦因数交互影响不显著。

2.4 最优参数组及仿真验证

利用Design-Expert软件的优化功能，以实测休止角42.4°为目标对回归模型进行寻优，所得出的优化解并非唯一解，而是若干组解。分别采用这些优化解进行土壤堆积仿真试验验证，选取与土壤实测堆数据最为近似的一组最优解：土壤JKR表面能为12.73 J/m2、土壤-土壤恢复系数为0.55、土壤-土壤静摩擦因数为0.84，其余非显著性参数取GEMM数据库的推荐值。

优化解下休止角仿真试验结果与实测试验结果对比如图5所示，仿真与实测试验得到的土壤颗粒在形状和相关数值上均无明显差异（>0.05），4次重复仿真试验得到土壤休止角为43.5°、41.8°、43.9°、42.3°，均值为42.9°，标准偏差为0.87°，与实测试休止角的相对误差（实测休止角为标准值）仅为1.2%，结果表明应用显著性分析和响应曲面法相结合的方法优化土壤颗粒仿真物理参数是可行的。

图5 堆积试验结果

3 穴孔成型试验验证

3.1 试验目的

为验证经过参数标定优化后构建的黏壤土离散元仿真模型是否能够准确反映土壤的物理力学特性，结合土槽试验和离散元仿真试验进行穴孔成型试验，以成型穴孔的开口纵长和有效深度为响应值，将实测值与仿真值进行对比分析，利用相对误差值判断离散元仿真模型的精准性。

3.2 试验方法与指标

3.2.1 穴孔成型土槽试验

土槽试验在湖南农业大学农业机械化工程实训中心试验土槽开展，为保障多次试验中土槽土壤条件的一致性，每次试验前对土槽土壤依次进行：刮土板刮平、旋耕机旋耕、刮土板刮平、喷淋系统洒水、镇压辊压实等处理。测定土壤参数：土壤较平整，土壤比重2 680 kg/m3，含水率为15.8%，0～160 mm深度土壤坚实度为185.6 kPa、土壤孔隙度为48.7%。

试制图6a所示成穴装置试验样机，样机作业参数如下：滚动半径260 mm，穴刺直径35 mm，锥尖倒角65°，入土深度68 mm。

图6 土槽试验

土槽试验进行4次平行试验，每次试验设定机具的前进速度为1.68 km/h，单次试验机具前进30 m，测定单次试验运行的中间段5 m内的穴孔的开口纵长和有效深度，记为单次试验的数值结果，取4次平行试验均值记为最终的数值结果，并计算其标准偏差。

开口纵长：测定成型穴孔上部端面沿着装置前进方向的长度，记为开口纵长。

有效深度：沿着成型穴孔端面到穴孔内部纵长为35 mm位置平面的垂直高度，记为有效深度。

相对误差：土槽试验和仿真试验结果的相对误差，以仿真模拟得出的数值为标准值，相对误差均取绝对值。

3.2.2 穴孔成型仿真试验

采用Pro/E 5.0软件按照1∶1比例建立成穴装置三维模型，简化模型并导入EDEM软件，试验装置的材料为钢材，本征参数为：密度7.85×103kg/m3，泊松比0.3，剪切模量7.0×107kPa。

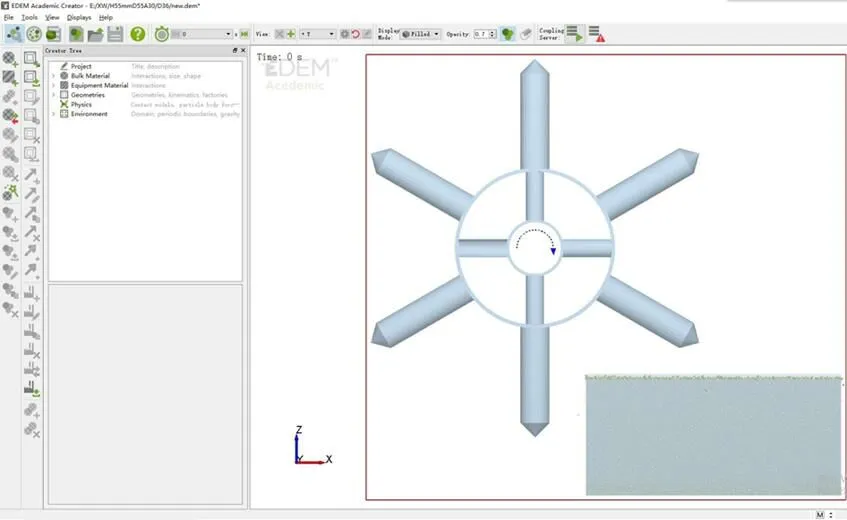
a. 穴孔成型仿真装置

a. Simulation device of hole forming

b. 仿真成型穴孔

在EDEM软件中建立土槽模型，其尺寸（长´宽´高）为350 mm´250 mm´180 mm，按照标定优化后的土壤物理参数在土槽模型中模拟生成高度为160 mm的土壤（土壤生成过程中，采用一定程度压实以实现土壤孔隙度48.7%）。EDEM仿真模型初始状态如图7a所示，成穴装置位于土槽左上端。

设定成穴装置以2 rad/s进行顺时针转动，其水平前进（向右平动）速度为0.468 m/s。进行4次仿真穴孔成型平行试验，测定成型穴孔的开口纵长和有效深度，取4次平行试验数值的均值记为仿真试验结果，并计算其标准偏差。

3.3 试验结果与分析

土槽试验成型穴孔如图6b所示，仿真试验成型穴孔如图7b所示。成穴装置成穴的土槽试验与仿真试验的结果对比如表7所示，结果表明：基于JKR接触模型，结合EDEM软件的GEMM数据库推荐的物理参数范围值，利用代理模型进行黏壤土离散元仿真模型参数标定及优化后，触土部件在仿真土壤模型中运动规律与土槽试验中差异较小，成型穴孔的开口纵长和有效深度的误差分别为3.98%和1.87%，仿真土壤的物理力学特性与实际土壤一致，从而表明黏壤土的离散元仿真参数系统标定研究的方法准确可行。

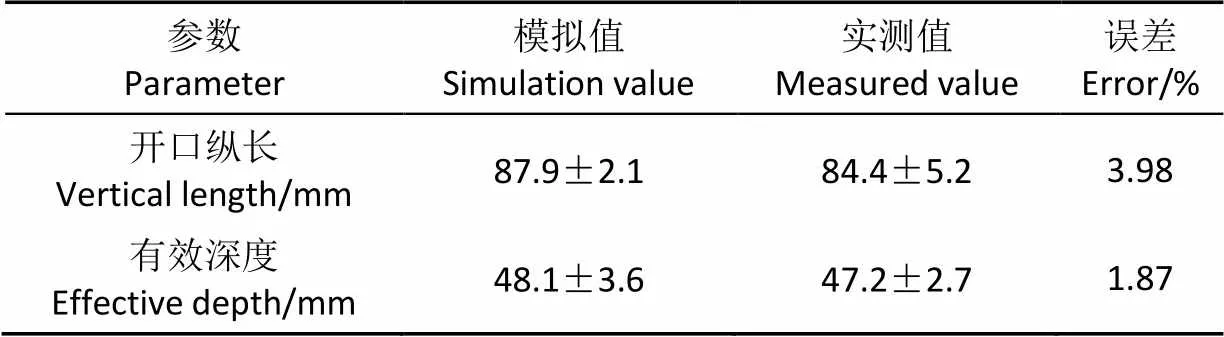
表7 仿真与土槽试验结果对比

4 结 论

本文基于土壤堆积试验，采用实测试验与离散元仿真相结合的方法，结合EDEM软件对中国南方地区种植土壤黏壤土进行仿真参数标定及优化，以休止角为响应值，借助Design Expert软件，将显著性分析和响应面法应用于仿真参数的优化求解，筛选出对休止角影响显著的物理参数，分析影响休止角的参数间的交互作用，确定最优参数。进一步通过穴孔成型的仿真试验与土槽试验对比分析，验证黏壤土离散元仿真模型反映土壤物理力学特性的准确性。得出如下结论：

1）仿真模拟的Plackett-Burman试验结果表明，仿真物理参数中土壤JKR表面能、土壤-土壤恢复系数、土壤-土壤静摩擦因数对土壤休止角影响显著；而其他物理参数对土壤休止角无显著性影响。

2）仿真模拟的Box-Behnken试验结果表明，3个显著性参数的一次项（土壤JKR表面能、土壤-土壤恢复系数、土壤-土壤静摩擦因数）和二次项（土壤JKR表面能和土壤-土壤恢复系数交互项、土壤-土壤静摩擦因数）对土壤休止角影响显著。对二阶回归模型求解，得出黏壤土仿真参数最优值：土壤JKR表面能12.73 J/m2、土壤-土壤恢复系数和静摩擦因数分别为0.55、0.84，其余非显著性参数取GEMM数据库推荐值，土壤泊松比0.38、土壤-土壤滚动摩擦因数0.1、土壤-钢材恢复系数、静摩擦因数和滚动摩擦因数分别为0.3、0.6和0.1。

3）成穴装置成穴的仿真试验与土槽试验的对比结果表明，利用代理模型进行黏壤土离散元仿真参数标定及优化后，成穴装置在土壤仿真模型中运动规律与土槽试验中差异较小，成型穴孔物理尺寸的数值差异在3.98%以内，仿真模拟土壤的物理力学特性与实际土壤一致。本研究探索出土壤离散元仿真物理参数系统标定及优化的方法，构建中国南方地区黏壤土精准的离散元仿真模型，为该类型土壤与触土部件相互作用下的动力学研究提供理论基础与技术支撑。

[1] 李博，陈军，黄玉祥．机械与土壤相互作用的离散元仿真研究进展[J]．农机化研究，2015，37(1)：217－222．Li Bo, Chen Jun, Huang Yuxiang. Research progress of discrete element simulation of soil-machine interaction[J]. Journal of Agrucultural Mechanization Research, 2015, 37(1): 217－222. (in Chinese with English abstract)

[2] 王学振，岳斌，高喜杰，等．深松铲不同翼铲安装高度时土壤扰动行为仿真与试验[J]．农业机械学报，2018，49(10)：124－136．Wamg Xuezhen, Yue Bin, Gao Xijie, et al. Discrete element simulations and experiments of disturbance behavior as affected by mounting height of subsoiler’s wing[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(10): 124－136. (in Chinese with English abstract)

[3] 马帅，徐丽明，邢洁洁，等．叶轮旋转式葡萄藤埋土单边清除机研制[J]．农业工程学报，2018，34(23)：1－10．Ma Shuai, Xu Liming, Xing Jiejie, et al. Development of unilateral cleaning machine for grapevine buried by soil with rotary impeller[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(23): 1－10. (in Chinese with English abstract)

[4] 贾洪雷，刘行，余海波，等．免耕播种机凹面爪式清茬机构仿真与试验[J]．农业机械学报，2018，49(11)：68－77．Jia Honglei, Liu Hang, Yu Haibo, et al. Simulation and experiment on stubble clearance mechanism with concave claw-type for no-tillage planter[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(11): 68－77. (in Chinese with English abstract)

[5] Zdancevičius E, Kačianauskas R, Zabulionis D. Improvement of viscoelastic damping for the hertz contact of particles due to impact velocity[J]. Procedia Engineering, 2017, 172: 1286－1290.

[6] Buechler S R, Mustoe G G W, Berger J R, et al. Under-standing the soil contact problem for the LWD and static drum roller by using the DEM[J]. Journal of Engineering Mechanics-Asce, 2012, 138(1): 124－132.

[7] 方会敏，姬长英，Farman A C，等．基于离散元法的旋耕过程土壤运动行为分析[J]．农业机械学报，2016，47(3)：22－28． Fang Huimin, Ji Changying, Farman A C, et al. Analysis of soil dynamic behavior during rotary tillage based on distinct element method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(3): 22－28. (in Chinese with English abstract)

[8] Janda A, Ooi J Y. DEM modeling of cone penetration and unconfined compression in cohesive solids[J]. Powder Technology, 2016, 293: 60－68.

[9] 黄玉祥，杭程光，苑梦婵，等．深松土壤扰动行为的离散元仿真与试验[J]．农业机械学报，2016，47(7)：80－88．Huang Yuxiang, Hang Chengguang, Yuan Mengchan, et al. Discrete element simulation and experiment on disturbance behavior of subsoiling[J]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(7): 80－88. (in Chinese with English abstract)

[10] 袁全春，徐丽明，邢洁洁，等．机施有机肥散体颗粒离散元模型参数标定[J]. 农业工程学报，2018，34(18)：21－27．Yuan Quanchun, Xu Liming, Xing Jiejie, et al. Parameter calibration of discrete element model of organic fertilizer particles for mechanical fertilization[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(18): 21－27. (in Chinese with English abstract)

[11] 石林榕，孙伟，赵武云，等．马铃薯种薯机械排种离散元仿真模型参数确定及验证[J]. 农业工程学报，2018，34(6)：35－42．Shi Linrong, Sun Wei, Zhao Wuyun, et al. Parameter determination and validation of discrete element model of seed potato mechanical seeding[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(6): 35－42. (in Chinese with English abstract)

[12] Mak J, Chen Y, Sadek M A. Determining parameters of a discrete element model for soil-tool interaction[J]. Soil and Tillage Research, 2012, 118: 117－122.

[13] Li Bo, Chen Ying, Chen Jun. Modeling of soil-claw interaction using the discrete element method (DEM)[J]. Soil and Tillage Research, 2016, 158: 177－185.

[14] Chen Y, Munkholm L J, Nyord T. A discrete element model for soil-sweep interaction in three different soils[J]. Soil and Tillage Research, 2013, 126: 34－41.

[15] Xiao Xiangwu, Tan Yuanqiang, Zhang Hao, et al. Experimental and DEM studies on the particle mixing performance in rotating drums: Effect of area ratio[J]. Powder Technology, 2017, 314: 182－194.

[16] Coetzee C J, Els D N J. Calibration of discrete element parameters and the modelling of silo discharge and bucket filling[J]. Computers & Electronics in Agriculture, 2009, 65(2): 198－212.

[17] Grima A P, Wypych P W. Development and validation of calibration methods for discrete element modelling[J]. Granular Matter, 2011, 13(2): 127－132.

[18] 刘凡一，张舰，李博，等．基于堆积试验的小麦离散元参数分析及标定[J]．农业工程学报，2016，32(12)：247－253．Liu Fanyi, Zhang Jian, Li Bo, et al. Calibration of parameters of wheat required in discrete element method simulation based on repose angle of particle heap[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016,32(12): 247－253. (in Chinese with English abstract)

[19] 刘凡一，张舰，陈军．小麦籽粒振动筛分黏弹塑性接触模型构建及其参数标定[J]．农业工程学报，2018，34(15)：37－43．Liu Fanyi, Zhang Jian, Chen Jun. Construction of visco-elasto-plasticity contact model of vibratory screening and its parameters calibration for wheat[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(15): 37－43. (in Chinese with English abstract)

[20] Uchul M, Fielke J M, Saunders C. 3D DEM tillage simulation: Validation of a hysteretic spring (plastic) contact model for a sweep tool operating in a cohesionless soil[J]. Soil and Tillage Research, 2014, 144: 220－227.

[21] Ucgul M, Fielke J M, Saunders C. Three-dimensional discrete element modelling (DEM) of tillage: Accounting for soil cohesion and adhesion[J]. Biosystems Engineering, 2015, 129(1): 298－306.

[22] 张锐，韩佃雷，吉巧丽，等．离散元模拟中沙土参数标定方法研究[J]．农业机械学报，2017，48(3)：49－56．Zhang Rui, Han Dianlei, Ji Qiaoli, et al. Calibration methods of sandy soil parameters in simulation of discrete element method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(3): 49－56. (in Chinese with English abstract)

[23] 王宪良，胡红，王庆杰，等．基于离散元的土壤模型参数标定方法[J]．农业机械学报，2017，48(12)：78－85． Wang Xianliang, Hu Hong, Wang Qingjie, et al. Calibration method of soil contact characteristic parameters based on DEM theory[J]. Transactions of the Chinese Society of Agricultural Machinery, 2017, 48(12): 78－85. (in Chinese with English abstract)

[24] 武涛，黄伟凤，陈学深，等．考虑颗粒间黏结力的黏性土壤离散元模型参数标定[J]．华南农业大学学报，2017，38(3)：93－98．Wu Tao, Huang Weifeng, Chen Xueshen, et al. Calibration of discrete element model parameters for cohesive soil considering the cohesion between particles[J]. Journal of South China Agricultural University, 2017, 38(3): 93－98. (in Chinese with English abstract)

[25] 王金武，唐汉，王奇，等．基于EDEM 软件的指夹式精量排种器排种性能数值模拟与试验[J]．农业工程学报，2015，31(21)：43－50． Wang Jinwu, Tang Han, Wang Qi, et al. Numerical simulation and experiment on seeding performance of pickup finger precision seed-metering device based on EDEM[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(21): 43－50. (in Chinese with English abstract)

[26] 戚江涛，蒙贺伟，坎杂，等．基于EDEM 的双螺旋奶牛饲喂装置给料性能分析与试验[J]．农业工程学报，2017，33(24)：65－71． Qi Jiangtao, Meng Hewei, Kan Za, et al. Analysis and test of feeding performance of dual-spiral cow feeding device based on EDEM[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(24): 65－71. (in Chinese with English abstract)

[27] 高国华，马帅．基于离散单元分析与物场分析的盆花移栽手爪优化[J]．农业工程学报，2017，33(6)：35－42．Gao Guohua, Ma Shuai. Improvement of transplanting manipulator for potted flower based on discrete element analysis and Su-field analysis[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2017, 33(6): 35－42. (in Chinese with English abstract)

[28] 朱德泉，李兰兰，文世昌，等．滑片型孔轮式水稻精量排种器排种性能数值模拟与试验[J]．农业工程学报，2018，34(21)：17－26． Zhu Dequan, Li Lanlan, Wen Shichang, et al. Numerical simulation and experiment on seeding performance of slide hole-wheel precision seed-metering device for rice[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2018, 34(21): 17－26. (in Chinese with English abstract)

[29] Zhong Wenqi, Yu Aibing, Liu Xuejiao, et al. DEM/CFD-DEM modelling of non-spherical particulate systems: Theoretical developments and applications[J]. Powder Technology, 2016, 302: 108－152.

[30] 石林榕，赵武云，孙伟．基于离散元的西北旱区农田土壤颗粒接触模型和参数标定[J]．农业工程学报，2017，33(21)：181－187． Shi Linrong, Zhao Wuyun, Sun Wei. Parameter calibration of soil particles contact model of farmland soil in northwest arid region based on discrete element method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(21): 181－187. (in Chinese with English abstract)

[31] 贺一鸣，向伟，吴明亮，等．基于堆积试验的壤土离散元参数的标定[J]．湖南农业大学学报：自然科学版，2018，44(2)：216－220． He Yiming, Xiang Wei, Wu Mingliang, et al. Parameters calibration of loam soil for discrete element simulation based on the repose angle of particle heap[J]. Journal of Hunan Agricultural University: Natural Sciences, 2018, 44(2): 216－220. (in Chinese with English abstract)

[32] 罗帅，袁巧霞，GOUDA Shaban，等．基于JKR粘结模型的蚯蚓粪基质离散元法参数标定[J]．农业机械学报，2018，49(4)：343－350．Luo Shuai, Yuan Qiaoxia, Gouda S, et al. Parameters calibration of vermicomposting nursery substrate with discrete element method based on JKR contact model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(4): 343－350. (in Chinese with English abstract)

中国农业工程学会会员：吴明亮（E041200186S）

Calibration of simulation physical parameters of clay loam based on soil accumulation test

Xiang Wei1,2, Wu Mingliang1※, Lü Jiangnan2, Quan Wei1, Ma Lan2, Liu Jiajie2

(1.,,410128;2.,,410205,)

In order to obtain the precise physical parameters of the discrete element simulation model of typical cultivated soil clay loam in southern China, this paper constructed a soil discrete element simulation model. Based on a soil accumulation test, this study proposed a method for combining the significance analysis and response surface method, which calibrated and optimized the simulation parameters of clay loam in southern China. Combining the results of actual test and GEMM database parameters recommended by constructing the DEM model of the soil, repose angle of soil was taken as response value, using the Design Expert software through the Plackett-Burman test, the steepest climbing test and Box-Behnken test, simulation physical parameters were calibrated and optimized. The simulation model of discrete element in clay loam was verified to be accurate by analyzing the simulation and soil bin testing of hole forming device. The DEM model of soil was established on the basis of the parameters determined by the basic test. The 8 initial physical parameters were screened for significance using the Plackett-Burman test. The results show that: the surface energy of soil for JKR model, soil-soil restitution coefficient, and the soil-soil static friction coefficient have significant effects on the response value and repose angle. Based on the optimal interval value of the significant parameters are determined by the steepest ascent test and the Box-Behnken test result, the quadratic regression model of significance parameters and repose angle is established and optimized to obtain the optimal combination of the significance parameters: The surface energy of soil for JKR model is 12.73 J/m2. The soil-soil restitution coefficient is 0.55. The soil-soil static friction coefficient is 0.84. Other insignificance parameters are as recommended by the GEMM database (Poisson's ratio of soil is 0.38. Soil-soil rolling friction coefficient is 0.1. Soil-steel restitution coefficient is 0.3. Soil-steel static friction coefficient is 0.6. Soil-steel rolling friction coefficient is 0.1). By the analog simulation of optimal parameter combination, it can be obtained that the simulated repose angle is 42.9° and the measured repose angle is 42.4°, therefore, the relative error is only 1.2%. There is no significant difference in shape and relevant value between the soil in simulation and the soil in experiment (>0.05). The optimized parameters can be used for further DEM analog simulation between the clay loam and the soil-contacting components and revealing the law of motion of clay loam under the action of soil-contacting components. The results of the simulation and soil bin testing of hole forming device show that, motion law of the soil-engaging component in the simulated soil model is slightly different from that in the soil groove test, with the numerical difference within 3.98%, which proves that the soil simulation model after parameter calibration and optimization can accurately replace the real soil for simulation. The research can provide theoretical basis and technical support for the dynamic study of the interaction between this type of soil and the contact soil components.

models; discrete element method; clay loam; parameter calibration; repose angle; simulation parameters; Johoson-Kendall-Roberts contact model

10.11975/j.issn.1002-6819.2019.12.014

S152.9；TP391.9

A

1002-6819(2019)-12-0116-08

2019-01-10

2019-05-17

国家科技支撑计划（2014BAD11B03）；湖南省科技厅重点项目（2017NK2131）；国家麻类产业技术体系项目（CARS-16-E21）；中国农业科学院科技创新工程项目（CAAS-ASTIP-2016-IBFC）

向伟，博士，助理研究员，主要从事农业机械创新设计。Email：xwxblg@163.com

吴明亮，教授，博士生导师，主要从事农业机械研究。Email：mlwu@hunau.edu.cn

向 伟，吴明亮，吕江南，全 伟，马 兰，刘佳杰. 基于堆积试验的黏壤土仿真物理参数标定[J]. 农业工程学报，2019，35(12)：116－123. doi：10.11975/j.issn.1002-6819.2019.12.014 http://www.tcsae.org

Xiang Wei, Wu Mingliang, Lü Jiangnan, Quan Wei, Ma Lan, Liu Jiajie. Calibration of simulation physical parameters of clay loam based on soil accumulation test[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(12): 116－123. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.12.014 http://www.tcsae.org