宇宙大尺度结构空洞的演化研究∗

赵 飞 罗 煜 韦成亮

(1 中国科学院紫金山天文台星系宇宙学与暗能量实验室 南京 210034)

(2 中国科学技术大学天文与空间科学学院 南京 210034)

1 引言

宇宙中的物质分布在大尺度上形成了非常复杂的网络状的结构,一般我们把这些大尺度结构分为空洞(void)、墙结构(wall)、纤维结构(filament)、团块结构(cluster)等.空洞结构的体积大约占宇宙总体积的80%,自从1978年人类第1次从星系巡天中发现空洞结构以来[1],人们便开始考虑利用空洞来研究宇宙学,以作为星系等其他宇宙学探针的补充.

空洞结构在宇宙学方面有非常重要的潜在应用价值.空洞的尺度跨度比较大[2–4],从1 Mpc到100 Mpc都有,这使得我们能够同时在不同尺度上研究宇宙.空洞结构内部的密度非常低,重子物质的质量占比相对较少,故其内部的动力学可能由暗能量主导,这使得我们能够用空洞结构来研究暗能量的属性,限制暗能量的状态方程[5–10].此外,空洞内部密度低,故修改引力理论如F5(Fifth force)等的效果更容易在其内部体现出来,因此空洞是检验修改引力理论的一个非常好的探针[11–15].空洞的统计性质对中微子的质量比较敏感,通过空洞来限制中微子的质量也是颇受关注的问题[16–18].空洞结构包含了宇宙大尺度结构形成的信息,可以用来做Alcock-Paczynski检验[19–20].如与宇宙微波背景结合,可以用来研究累积萨克斯-沃尔夫(ISW)效应[21–26].此外,空洞结构的尺度和红移畸变的尺度相近,这使得空洞结构还能用来研究红移畸变[27–32].

尽管空洞有很多潜在的应用价值,但目前这方面有很多问题尚未解决.其一是我们对空洞这一概念没有一个严格的定义,我们对空洞的研究主要是数值模拟主导的,每个人的算法或多或少存在差异,以致不同研究者之间的结果存在差异,互相之间不好比较[33–37],二是我们没有一个和实际模拟以及观测数据相符合的完善的空洞理论模型[38–42].

空洞理论模型的建立主要借鉴了暗物质晕的理论模型,为进一步完善空洞的理论模型,从数值模拟角度出发研究其演化是一个非常好的思路,能够为构建理论模型提供一些数据支撑.而目前空洞演化研究还尚未成熟[43–46],Sutter等[43]以及Wojtak等[44]通过借鉴暗物质并合树的方法来研究空洞的演化,这些研究整体上定性给出空洞演化的物理图像,即相对暗物质等高密度结构而言,空洞的演化过程没有那么剧烈,从数值模拟的初始条件红移z=100开始直到z=0时刻,在跨度如此大的红移区间内,空洞基本上保持了最初的位置,空洞随红移逐渐缓慢地膨胀变大,最后体积大概增加20%左右.在演化过程中,空洞的形状分布整体改变很小,其形状有比较弱的变扁趋势.其主轴的指向也大体保留了初始时刻的指向.Sutter等[43]和Wojtak等[44]工作的结果也有不同之处,Sutter等[43]的结果是空洞的演化历史和其等级结构更加相关,与空洞大小关系比较弱,而Wojtak等[44]的演化轨迹主要是由空洞的大小决定的.这其中的差异主要是他们选择的具体空洞样本以及追踪空洞的起源等方法上的不同所致.即空洞演化在细节上的结果是依赖于研究方法的.

之前关于空洞演化的研究主要关注暗物质空洞的演化,但是暗物质空洞和星系空洞之间的统计性质存在差别[47–51],这主要源自星系偏袒,即星系分布不能精确代表宇宙所有物质的分布.Kreisch等[17]在研究空洞的统计性质对中微子质量响应的时候,发现不同示踪物找出来的空洞大小分布对中微子质量的响应是相反的.这说明搞清楚不同示踪物找出来的空洞之间的差别非常重要.之前一些研究暗物质空洞和星系空洞的文章[47–48]指出,星系空洞和暗物质空洞大体上能够匹配得上,但是两者的质心会在统计上偏离大约空洞大小的50%.另外暗物质空洞和星系空洞的叠加密度轮廓非常相似,能够用Hamuas等人给出的公式拟合[52].在研究星系偏袒的时候,模拟粒子的数密度会带来非常大的影响,会掩盖掉星系偏袒造成的星系空洞的统计性质的差别[48].Pollina等[49–50]在研究星系、星系团、活动星系核(AGN)等空洞的偏差时,发现重子物质的空洞的叠加密度轮廓和其中的暗物质的叠加密度轮廓之间存在比值关系,该比值随着空洞的变大而逐渐减少,最后渐近于线性偏袒因子,偏袒因子即星系功率谱和暗物质功率谱的比值.

这里需要特别注意的是,目前研究中所讨论的关于星系空洞和暗物质空洞之间的差别由以下几个原因导致:(1)暗物质和星系之间真正由宇宙的物理演化过程所产生的偏袒,这部分是我们真正所关心的部分;(2)目前主流的基于Tesselation的空洞算法比如VIDE(Void Identification and Examination toolkit)将星系看作是等质量的粒子,在做Tesselation的时候没有考虑质量权重,这部分会引起噪声.没有考虑星系质量权重的主要原因有两点,一是目前真实巡天数据中的做法也是直接去数星系的数目而不考虑其质量权重,二是Mao等[53]指出,不同密度环境中的星系质量分布差别不是特别大;(3)示踪物的数密度不同所带来的误差.前人的研究往往忽略了这一点,即没有考虑不同示踪物之间的粒子数密度不同所带来的影响.Sutter等[48]在研究示踪物的粒子数密度对空洞统计性质影响的时候发现,当示踪物的粒子数密度比SDSS DR7(Sloan Digital Sky Survey Data Release 7)的星系数密度(约为10−2Mpc−3·h−1,h为无量纲哈勃常数)低的时候会带来比较大的系统性误差,主要体现在对空洞统计性质的系统性影响,而更高的示踪粒子数密度给出的结果比较稳定.因此目前设置示踪物粒子数密度的时候以SDSS DR7对应的值为参考或更高.

前人关于示踪物导致的空洞统计性质差别的相关研究包含了上述3个方面,而本文在研究示踪物偏差的时候将不同示踪物的粒子数密度设置为相等,这样就避免了示踪物数密度不同所带来的不确定性,即本文中的偏袒只包含真实的示踪物之间的偏袒且没有考虑星系质量权重所带来的噪声.另外,前人关于示踪物的研究主要关注红移z=0处的星系空洞和暗物质空洞统计性质之间的差别,或者研究一些真实的星系巡天数据如SDSS数据的开源空洞列表[53–56],在本文的工作中,基于密度场极小值这一空洞的最基本的定义,我们系统研究了暗物质和星系示踪物找出来的空洞的统计性质的差别及其随时间的演化.此外,本文中使用了比较高的示踪物数密度(约是SDSS DR7星系数密度的100倍),这样能够更好地解析小的空洞,以便于对空洞的理论模型的完善提供借鉴.本文接下来的第2部分主要介绍我们使用的空洞结构算法,第3部分主要介绍我们使用的数据,第4部分主要介绍我们的研究结果,最后是总结和讨论.

2 VIDE算法

空洞的算法多种多样[57–61],不同的算法给出的结果还或多或少存在差异[33,37],这也是目前空洞领域比较棘手的问题.但是相对而言,目前使用比较多的算法是Sutter等[57]的开源程序VIDE,VIDE是一个优化版的ZOBOV(ZOnes Bordering On Voidness)[58].并且其模块化程度比较高,易于根据自己的需要修改.

VIDE的基本思路分为4个步骤:

(1)生成维诺图(Voronoi Tesselation)[62].对于一个离散的粒子集,我们给每个粒子生成一个小多面体,该多面体按照如下规则确定: 对于该体元内部的任意点,其与该粒子的距离比其他粒子与该粒子的距离都要小.该体元的倒数就是该位置处粒子的局域密度值,这样一来就得到了一个以每个粒子为中心的密度场.

(2)寻找密度极小值点.对于第1步给出的密度场,我们找出所有的密度极小值点.密度的极小值点按照如下定义: 如果某个粒子的局域密度比所有与它相邻的粒子的局域密度都要低,那么这个粒子的位置就认为是密度场的极小值点.

(3)建立局域的低密度区域.以第2步给出密度场的每个极小值点为中心向四周扩散,把所有相邻的并且密度更高的体元连接起来,在连接的过程中不断以边界的体元为准进行迭代扩张,直到没有更高密度的相邻体元.如此则给出了围绕每个密度极小值的局域的低密度区域.这些局域的低密度区域就可以认为是空洞结构.

(4)分水岭变换(Watershed transform)[60].这一步骤对第3步得到的局域低密度区使用分水岭算法进行连接,从而形成更大的空洞结构.这种分水岭算法也给出了空洞结构的等级结构,根据其包含与被包含的关系,我们将之称为父空洞结构和子空洞结构.所谓的父空洞是不被其他空洞包含的空洞,而子空洞是被其他空洞结构包含的空洞.我们用等级深度来表示被包含的层次,不被包含的父空洞的等级结构深度为0,被包含一次的等级深度为1,依此类推.

VIDE程序给出来的空洞是通过成员粒子集合来表示的,其形状是不规则的.而一些情况下我们需要对大量空洞样本进行叠加,这首先要求我们确定空洞的中心,比较常见的确定空洞中心的方法有两种,一种是把空洞密度最低的位置(即体积最大的成员粒子的位置)定义为中心,而另一种方法则是将空洞成员粒子的质心定义为中心(所有维诺体元的体积加权的中心):

其中xi是空洞结构的第i个成员粒子的位置,而Vi则是对应的维诺体元的体积.对空洞中心本文中使用上述定义.

另外,由于VIDE给出的空洞形状是不规则的,这给空洞的叠加以及衡量空洞的尺度带来了不便,对于空洞尺度我们使用有效半径Reff来描述其大小,其定义如下:

其中V是空洞结构的体积(所有维诺体元的体积之和),即空洞的有效半径是与空洞真实体积相等的球的半径,在本文后面的内容中,我们统一使用有效半径来表示空洞结构的大小.另外,我们在叠加空洞的时候也是以(1)式计算的中心为准对齐,参与叠加的粒子是Reff内的粒子.

上述算法的第4步分水岭变换即是以密度场极小值为中心的局域低密度区域的扩展,通过这一步空洞形成了复杂的等级结构.但问题也是恰恰在这一步产生,即如何扩展目前并无定论.最常见的情况是根据低密度区域之间的分隔区域的密度高低和人为设定的阈值来比较以确定是否扩展.而常用的阈值选择之一是0.2,即当两个低密度区域之间的分隔区域的密度低于整个模拟体积密度的0.2倍的时候满足扩展条件.另外一种策略是将该阈值设置为无穷大,如此一来,密度值最小的低密度区域会将其他所有的低密度区吞噬,其结果是空洞的体积加起来超过了整个模拟体积,很显然这是不太合适的.

Nadathur等[37]在对比空洞的性质和理论模型预言的时候,将并合阈值设为0,即不考虑密度极小值区域的扩展,空洞列表由上述算法的第3步得到的局域低密度区域构成.Nadathur的初衷是这种做法在建立理论模型的时候可能更好处理.除此之外,这种做法很适用于我们研究空洞的演化,因为空洞的演化大体上是内部密度减小的过程,在不同红移处设置相同的并合阈值比如0.2显然是不合适的,而这种不考虑扩展只研究密度场极小值区域的做法对不同红移而言是比较合适的.

3 数据

我们使用的数据是一个高精度的N体宇宙学模拟的数据,该数值模拟是ELUCID(Exploring the Local Universe with the reConstructed Initial Density Field)项目的一部分[63–65].该模拟的粒子数是30723,模拟盒子的边长是500 Mpc,并使用周期性边界条件.宇宙学参数是WMAP9(Wilkinson Microwave Anisotropy)[66]的结果,具体的宇宙学参数值分别是: Ωm=0.282,Ωλ=0.718,Ωb=0.046,ns=0.965,h=0.697,σ8=0.817,质量分辨率是3.3747×108M⊙·h−1.该模拟起自红移100,从红移19到红移0处,在lg(1+z)空间中等间隔输出100个红移位置的数据.

基于该N体数值模拟,我们通过FOF(Friends of Friends)算法给出暗物质晕的列表,再基于此暗物质晕列表,通过半解析模型[67]给出了对应红移处的模拟星系列表.

为了研究空洞演化,我们在红移2.03到红移0之间总共取了6个红移位置的星系数据.图1给出的是6个红移位置处的星系数目Ngal,其中红移2.03处的星系数目为13495546,记作Ngal(z=2.03)=13495546,相应的数密度为0.1079 Mpc−3,星系在不同的红移处其数目略有变化,如图1所示.另外,由于暗物质粒子和星系粒子的数密度差异比较大,这会对研究星系空洞和暗物质空洞之间的偏袒带来影响[48],因此我们将6个红移位置处的暗物质粒子向下采样至和对应红移的星系相同的数密度,并且为了考虑泊松噪声的影响,我们还产生了对应的具有相同粒子数密度的泊松样本.本文使用的N体模拟数据以及基于此给出的半解析模拟星系皆是在共动坐标系下的结果,相关的坐标皆是共动坐标.

图1 不同红移处的星系数目的分布,其中Ngal(z=2.03)=13495546Fig.1 The distribution of galaxy number at different redshifts where Ngal(z=2.03)=13495546

4 结果与分析

图2给出的是空洞的大小和内部密度最小值的2维分布,图2中nmin是空洞内部密度最小值,是整个模拟体积的粒子平均数密度,之后相同的变量同此意.左边一列是暗物质空洞,右边一列是星系空洞,从上到下依次是从高到低的3个不同红移.空洞内部密度的最小值我们用整个模拟体积内部的粒子平均密度进行归一化处理.其中的虚线是由对应的泊松样本找出来的空洞2维分布等值线,其物理意义是该等值线内部包含了泊松样本的空洞数目的99%.从图2可以看出,相对同一红移处的暗物质空洞的分布,星系空洞的分布总是更加紧致,并且内部密度相对要低一些.另对比3行子图可以看出随红移的演化,我们找出来的空洞分布和泊松样本的空洞分布差别越来越大,从最后一行图中可以看出,在红移0处,我们的空洞样本几乎不受泊松噪声的影响.在高红移处,空洞样本的分布和泊松空洞样本的分布重合比较多.

图2 空洞内部密度最小值nmin和大小Reff的2维分布,右边的子图是星系空洞的分布,左边是暗物质空洞的分布.子图中的虚线内部包含了99%的泊松样本找出来的空洞.Fig.2 The distribution of void minimum density values nmin and effective radius Reff of the void samples defined from dark matter particles(left panels)and mock galaxies(right panels).Deshed line in each panel encloses 99 percent of voids found in poisson particles.

通常在研究空洞的时候,为保证结果的可靠,只选择部分比较显著的空洞样本作为研究对象.主要的评估空洞样本的稳健性有两种,一是根据空洞内部的最小密度,一般把该值设定为0.2[41].另外一种常见做法是Neyrinck[58]给出的由密度比来确定一个空洞是泊松噪声的概率P(r):

其中r表示密度比,其物理意义是空洞边界处的密度最小值和空洞内的密度最小值之比:

其中,min(nridge)是空洞边界处密度最小值,nmin是空洞内部密度最小值.常用做法是选择1.4作为阈值,对应的泊松噪声的概率约为12%.因为其他人只研究红移0左右的空洞,如此筛选仍然能够保留足够多的统计样本,然而对于不同红移的空洞来说,其密度处在演化的过程中,因此这种固定的阈值选择是不太合适的,尤其是以红移2.03处的暗物质空洞为例,如按照上述方法筛选将会大大减少样本中的空洞数量.因此,我们的空洞除了考虑粒子平均间隔的限制,对样本不做任何其他筛选,这样更加符合密度极小值的定义和我们的研究目标.

图3表示的是红移0处不同大小空洞的叠加密度轮廓,其中n(R)是空洞径向距离R处的平均粒子数密度.该叠加密度轮廓通过如下方法得到,即我们对每一个空洞计算其围绕质心球壳的密度,其中密度用样本平均粒子数密度归一化,半径则用其有效半径归一化,然后对所有的空洞样本平均,误差棒是标准误差.左边是暗物质空洞,右边是星系空洞.从图中我们可以看出星系空洞的叠加密度轮廓和暗物质空洞的叠加密度轮廓的差异非常明显,星系空洞的叠加密度轮廓更加陡峭,其内部密度更低,边界处的密度更高.并且不管是暗物质空洞还是星系空洞,都表现出来小的空洞整体密度更高这一特点.这说明小的空洞倾向于处在高密度区域,其背景密度相对更高.而大的空洞倾向于处在比较低密度的环境中.

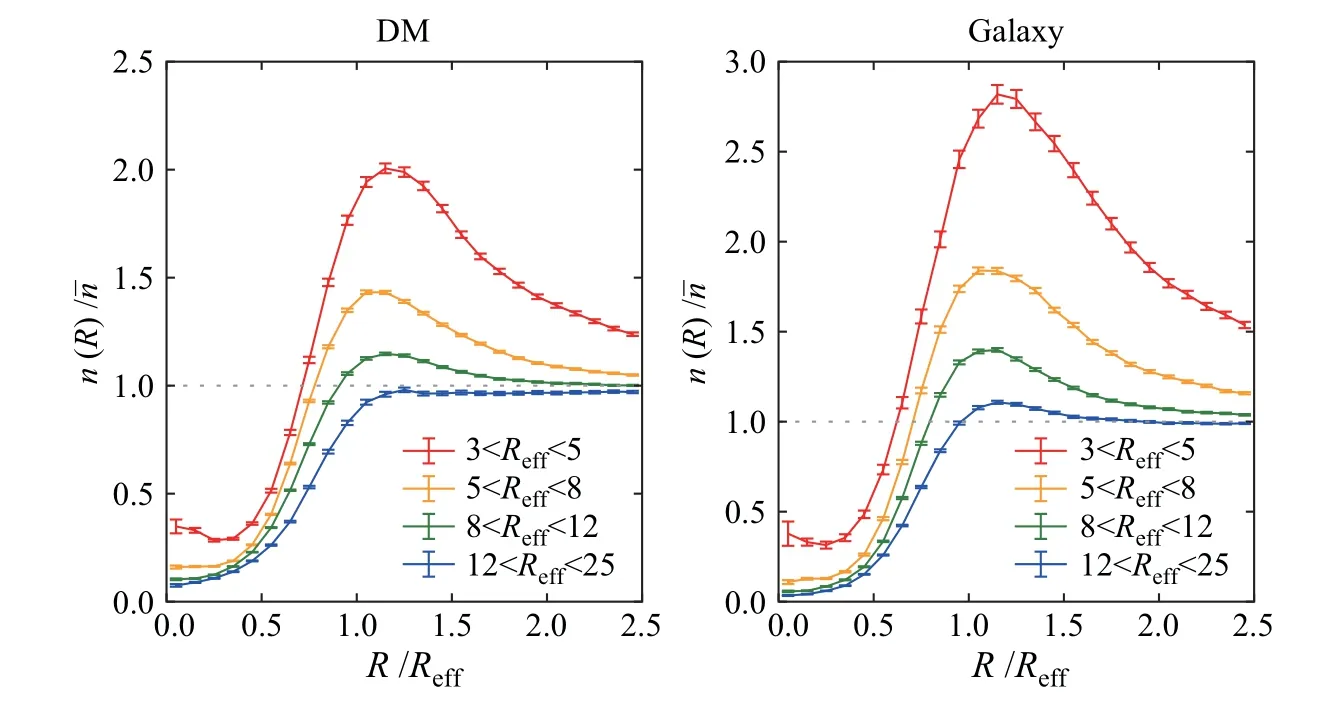
图3 红移0处空洞的叠加密度轮廓Fig.3 The stacked density profile of void at z=0

Hamaus等[52]结果显示的是大的空洞内部密度更高,小的空洞的内部密度更低,而在边界处的趋势则和我们的结果相同.关于空洞内部密度这一点,Hamaus等[52]没有做出特别的解释,我们的结果与之相反,本文和Hamaus等[52]的研究在定义空洞中心的方法上完全一样,其结果的差异主要是空洞算法的不同导致的,Hamaus等[52]的空洞包含了极小值区域的扩展,而我们的算法则没有.

此外我们发现小空洞中心处的密度有微小的翘起,而大空洞则没有,导致这一现象的主要原因是本文使用的空洞中心的定义方法((1)式)并不完全对应空洞内部密度最小值位置,小空洞倾向于处在高密度区域,其内部的密度轮廓更加陡峭,因此相对大空洞而言,质心位置和空洞内部密度最小值点的位置不重合会对中心的叠加密度轮廓带来更大的影响.

图4给出的是空洞的密度比和对应位置处用另一种示踪物的密度值计算出来的密度比的分布.图4中横坐标r即由(4)式计算,而纵坐标r′的计算方法是:

其中min(n3)是min(nridge)位置处最近邻的3个另一种示踪粒子的密度最小值,对于星系空洞则是暗物质粒子,反之亦然.空洞边界处密度的最小值和空洞的贯通并合直接相关,在空洞的演化进程中是一个非常重要的物理量.通过图4星系和暗物质两种示踪物找出来的不同大小的空洞密度比的分布可以看出,不论是暗物质空洞还是星系空洞,大空洞的密度比在分布上比小空洞的更高,因此小空洞相比大空洞,更加容易发生并合,其演化效应更加明显.另外对比图4中第1列子图和第3列子图可以发现,对于小空洞而言,星系空洞的密度比在分布上略微高于暗物质空洞.

图4 空洞的密度比r((4)式)和对应相同位置处用另一种示踪物的密度计算出来的密度比r′((5)式)的2维分布.左边两列给出的是暗物质空洞的密度比,右边两列则是星系空洞.所有子图中的虚线r′= r.Fig.4 The comparison between void density contrast r(Eq.(4))and the density contrast r′(Eq.(5))at the relative same position,calculated by another tracer,as shown in the left two columns for dark matter(DM)voids and the right two columns for galaxy voids.Dashed line indicates r′= r.

此外,在暗物空洞容易贯通的地方星系的密度更低,这体现在第1列子图中分布的峰值位置在直线r′=r以下,而对于大空洞而言,其容易贯通的位置处星系的密度和暗物质的密度相对接近.因为在大尺度结构的形成过程中,总是先形成暗物质场的高密度区域,然后再开始形成星系,表现出来的结果是星系更容易示踪暗物质空洞的一些很明显的墙结构,而不能很好地示踪暗物质空洞相对比较薄弱的墙结构,这导致了星系空洞提前贯通,这里提前贯通意为星系找出来的空洞通常更加显著,而在对应位置处暗物质会存在更多的小结构,使得通常会找到更多显著性更弱的小的暗物质空洞,在之后的演化过程中,这些小暗物质空洞容易发生并合.从图4中右边两列子图中可以看出,对于已经形成的星系空洞而言,即便是其墙上最薄弱的地方也往往堆积着显著的暗物质,使得星系的位置保持稳定,甚至形成新的星系,从而抑制星系的贯通.基于这个对比结果我们可以做出如下推断:(1)暗物质空洞数目要多于星系空洞数目,因为暗物质粒子能够解析更薄弱的墙结构;(2)暗物质空洞更容易并合,从而比星系的演化更快,特别是小的空洞;(3)空洞的并合会改变空洞的对称性,由于提前贯通,星系空洞的形状在统计上比暗物质空洞更扁一些;(4)由于演化速度的差异,暗物质空洞和星系空洞的统计性质最终会趋于一致.我们接下来对上述推断分别给予论证.

图5给出的是空洞的数目及其演化,其中Nv是空洞的数目,而Ndm和Ngal分别代表暗物质和星系空洞的数目.其中上面的子图给出是星系和暗物质两种示踪物找出来的空洞数目的变化,这里我们用高红移的数目对其进行了归一化.图中的点线代表的是泊松样本的空洞数目的变化,点划线是纵坐标为1的参照线,而其中黑色的菱形则是不同红移处产生的泊松样本的粒子数目,这里仍然用高红移的粒子数目做了归一化处理.可以看出,泊松样本中空洞数目的变化完全是泊松样本的粒子数目变化引起的,即泊松样本的空洞数目和泊松样本的粒子数目呈正比关系.这进一步确定了星系空洞和暗物质空洞各自的数目变化是宇宙演化的结果.另外可以看出,暗物质空洞数目的演化要比星系空洞的数目演化更加明显.

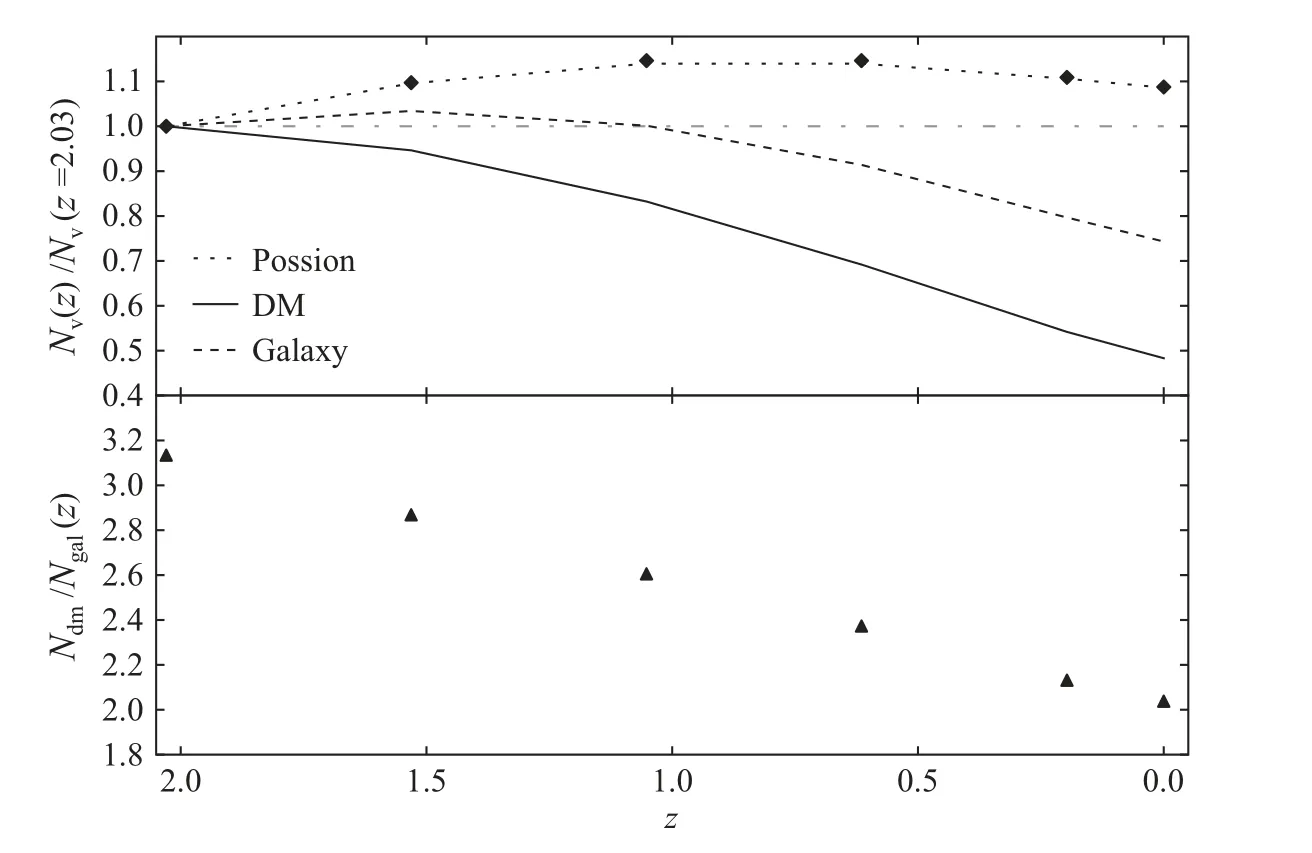
图5 上面的子图中展示的是空洞的数目随红移的分布,而暗物质空洞和星系空洞的数目的比值则在下面的子图中展示.此处的比值随红移线性变化.Fig.5 Top panel shows the distribution of void numbers as the function of redshift,and the ratio of void number of DM to galaxy is shown in the bottom panel.Here the result indicates that the ratio linearly changes with redshift.

图5下面的子图则给出的是暗物质空洞数目和星系空洞数目的比值随红移的演化.可以看出暗物质空洞的数目要多于星系空洞的数目,另外红移越低,它们之间的比值越小,即暗物质空洞的数目逐渐接近星系空洞的数目.以上的结果从空洞数目这一角度证实了上述几条推断的正确性.除此之外,该比值不仅随着红移定性地减小,还在我们研究的整个红移区间内随红移呈现出良好的线性关系.这使得我们能够定量地刻画星系偏袒所带来的空洞数目的差别,而不再是单纯地停留在定性的描述层面,这种良好的线性关系能够为空洞理论模型的完善提供很好的数据参考.Nadathur等[37]在对比z=0处分别由暗物质空洞和HOD(halo occupation distribution)模型[68]给出模拟星系数据找出来的空洞数目的差别的时候,发现星系偏袒会导致星系空洞的数目大概只有暗空洞数目的一半,图5中下面的子图在红移0处的比值为2,在这一点和我们的结果非常吻合,并且我们还给出了更高红移的数目差别.我们的研究和Nadathur等[37]的研究各自使用了不同精度的N体数值模拟以及不同的产生星系的模型,并且采样后的示踪物的绝对数密度也不同,Nadathur等[37]使用的粒子数密度和SDSS DR7数据给出的全部星系在共动坐标下的数密度相当,而我们的示踪粒子的数密度大约是100倍左右.尽管有这些区别,我们与Nadathur等[37]的研究在示踪物造成的空洞数目的偏袒上吻合得比较好.

图6给出的是空洞的大小分布随红移的演化,左边是暗物质空洞,中间是星系空洞,右边是暗物质空洞的分布和星系空洞的分布函数的比值.可以看出空洞在大小分布上的演化特点是小的空洞逐渐减少,大的空洞逐渐增多.不论是星系空洞还是暗物质空洞,小空洞的数目变化要比大空洞的数目变化更加明显.另外,对比暗物质空洞和星系空洞的演化我们可以发现,暗物质空洞的演化相对明显一些,而星系空洞的演化则非常平缓.随红移的演化,暗物质空洞的尺度函数的形状和星系的越来越接近.这也符合前面的推断.

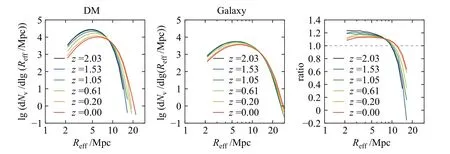
图6 不同红移处空洞有效半径的分布,左边是暗物质空洞,中间是星系空洞,右边则是二者的比值Fig.6 The distribution of void effective radius at different redshifts for DM voids(left panel)and galaxy void(middle panel).The right panel shows the ratio of DM void number to that of galaxy void

图7给出的是不同示踪物找出来的空洞大小及其随红移的演化,其中是空洞的平均有效半径,而分别是暗物质空洞和星系空洞的平均有效半径.上面的子图给出的是星系和暗物质两种空洞各自统计平均大小的演化.点线代表泊松样本空洞的大小变化,点划线是纵坐标为1的参照线,该变化完全是由于粒子数密度不同导致的,这说明星系和暗物质空洞的尺度变化是物质演化的结构.从图7中我们可以看出暗物质空洞和星系空洞都在逐渐变大,而暗物质的尺度演化更加明显,这正说明了小暗物质空洞的贯通并合要更容易发生.图7下面的子图给出的是暗物质空洞和星系空洞平均尺度的比值,可以看出星系空洞要更大一些,这是因为星系空洞提前贯通了,所以在尺度上要更大一些.而在随后的演化中,由于暗物质空洞比星系空洞并合得更快,使得暗物质空洞的尺度逐渐接近星系空洞的尺度.这正是之前推断的必然结果.此外,暗物质空洞和星系空洞尺度的比值随红移有很好的线性关系.结合图7空洞尺度的增加和图5空洞数目的减少我们可以估算出,不管是暗物质空洞还是星系空洞,其体积之和基本不随红移改变.另外,在相同红移处,星系空洞和暗物质空洞所占的总体积也相当.

图7 上面的子图展示的是空洞的有效半径随红移的变化,下面的子图中展示的是暗物质空洞的有效半径和星系空洞的有效半径的比值,该比值随红移呈现出线性变化.Fig.7 Top panel shows the distribution of void effective radius as the function of redshift,and the ratio of DM void effective radius to galaxy void effective radius is shown in the bottom panel.Here the result indicates that the ratio linearly changes with redshift.

从图7上面的子图中我们可以看出,在我们所研究的红移区间,暗物质空洞的平均大小增加了约25%,其体积大约增加了1倍.而之前的研究如Sutter等[43]以及Wojtak等[44]给出的结果是空洞的体积大约增长20%,这和我们的结果有所不同,此处的差异主要是空洞的算法以及所研究的空洞样本不同导致的.在Sutter等[43]和Wojtak等[44]的研究中使用的空洞算法包含第4步的VIDE(本文算法部分),而我们没有包含第4步,另外更加重要的区别是,Sutter等[43]和Wojtak等[44]只选取了几个尺度比较大且特别显著的空洞研究其演化,而本文则是基于大量空洞样本的统计研究.当只研究几个特别显著的空洞样本时,因这些空洞边界处的墙和纤维状结构比较密集,不容易被潮汐力瓦解,导致空洞的体积变化比较小.

图8给出的是空洞形状的演化.这里我们采用常用的借助惯性张量的方法来定义空洞的形状.即每一个空洞的形状是通过其成员粒子来估计的,根据成员粒子的位置,我们可以计算该空洞的惯性张量[57],其中的对角分量是:

而非对角分量的形式是

其中,Np是空洞结构成员粒子的数目,xi、yi、zi是第i个成员粒子相对空洞结构质心的坐标,惯性张量的其他分量则是该形式的轮换对称.然后通过求解惯性张量的本征值和本征矢可以计算空洞结构的椭率:

其中J1和J3分别是惯性张量的最大和最小本征值,其中0<ϵ<1,ϵ越大,说明空洞越扁.而Wojtak等人的研究[44]则使用了该方法的一种变体形式来计算形状,即先将整个模拟体积划分成规则的小网格,然后对其内部的网格点计算几何中心,这两种方法的区别在于是否有物质密度加权.我们的方法给出的是空洞物质分布的形状,而Wojtak等[44]的方法则给出的是空洞所占空间体积的形状.Wojtak等人的研究[44]发现暗物质空洞在高红移的时候形状几乎不改变,而在红移2.03到红移0之间,空洞的形状有微弱的变扁趋势.

图8 上面的子图展示的是空洞的平均椭率随红移的变化,而下面的子图则是暗物质空洞的平均椭率和星系空洞的椭率的比值,该比值随红移呈现出线性变化的特点.Fig.8 Top panel shows the distribution of void mean value of ellipticity as the function of redshift,and the ratio of DM void ellipticity to galaxy void ellipticity is shown in the bottom panel.Here the result indicates that the ratio linearly changes with redshift.

我们采用了惯性张量的方法计算空洞形状,图8上面的子图给出的是暗物质空洞和星系空洞椭率的演化.暗物质空洞和星系空洞都随红移逐渐变得越来越扁,如空洞的数目和大小一样,星系空洞的椭率演化也相对弱一些,这一演化趋势和前述几条推断是自洽的,即空洞的并合会破坏空洞的对称性,使其形状更扁.但是之前的理论认为,对于一个独立的、非球对称的空洞,其演化特点是逐渐变得越来越圆[69],这和我们数值模拟的结果相悖.理论模型给出这一结果是因为假定了空洞是独立的演化个体,其主要演化轨迹是要么膨胀变大要么塌缩成高密度区域而消失,具体服从哪种轨迹取决于空洞的内部密度和边界密度的关系,而不涉及空洞之间的相互作用.但实际上空洞处在极其复杂的宇宙大尺度网状结构中,一个空洞与周围的其他结构以及其他相邻的空洞是密切相关的[70],其演化是互相影响的.前人的结果发现单个空洞的演化不太明显[44],而我们的结果清楚显示空洞并合在演化中非常重要.这说明要完善空洞的理论模型需要建立空洞的并合模型.

图8下边的子图给出是暗物质空洞和星系空洞平均椭率的比值随红移的演化,ϵ代表空洞的椭率则分别代表暗物质空洞和星系空洞的椭率的均值.可以看出星系空洞的形状在分布上更扁一些,之后暗物质空洞的快速演化使其形状逐渐逼近暗物质空洞的形状,最后在红移0处,二者的平均椭率几乎一致.这里更加确信了前述几条推断的正确性.此外暗物质空洞的平均椭率和星系空洞的平均椭率的比值随红移也呈现出很好的线性关系.

空洞的叠加密度轮廓是空洞的一个非常重要的性质.目前大多数研究中对空洞叠加密度轮廓均做球对称假设[52],该假设认为大量空洞样本叠加起来应该是球形的,尽管单个空洞的形状可能非常不规则.这种球对称叠加方法可以用来做Alcock-Paczynski检验[19–20]及研究空洞的红移畸变[30–31],这也是目前为什么球对称叠加方法仍然是主要方法的原因.Cautun等人提出了一种等边界距离壳层叠加方法[71],这种方法实际上是对空洞边界的叠加密度轮廓的描述,Wojtak等人的研究[44]则使用了一种类似边界叠加的方法研究了暗物质叠加密度轮廓的演化特点,即对于膨胀变大的空洞,其叠加密度轮廓的演化可以分为两个过程,一是内部密度的降低,二是边界密度的升高.

我们在本文中使用了第1类叠加方法.图9给出的是空洞的叠加密度轮廓的演化,左边是暗物质空洞,右边是星系空洞,其中误差棒是标准误差.可以看出空洞内部的密度逐渐降低,而边界处的密度逐渐升高.可以看出暗物质空洞在演化上存在非常剧烈的物质从内部向外流动的过程,而星系空洞叠加密度轮廓的演化则非常弱,但演化趋势完全一致.虽然本文和Wojtak等[44]相比,使用了不同的叠加方法以及不同的空洞并合条件,但在叠加密度轮廓的演化趋势上完全吻合.这反映了从统计上来说空洞叠加密度轮廓的演化特点是比较确定的,对计算方法的依赖性不高.另外星系空洞内部的密度要比暗物质空洞的密度低,而边界处的密度则反之,综合来看星系空洞的叠加密度轮廓更加陡峭.

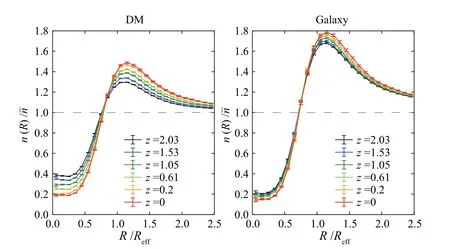
图9 不同红移处空洞的叠加密度轮廓.左图是暗物质空洞,右图是星系空洞Fig.9 The stacked density profile at different redshifts for DM voids(left panel)and galaxy voids(right panel)

图10中左边的子图则是使用暗物质空洞的大小和位置,但是使用星系得到的叠加密度轮廓,而右边的子图是使用星系空洞的大小和位置,但用暗物质粒子作为示踪物给出的叠加密度轮廓.通过右边的子图可以发现,利用星系示踪找出来的空洞在叠加密度轮廓随红移演化上不能真实反映其对应的暗物质空洞的性质.利用星系示踪找出的暗物质空洞与纯暗物质分布找出来的空洞的性质也存在差异.但是真实的数据中主要是星系巡天数据,因此进一步量化暗物质空洞和星系空洞的叠加密度轮廓之间的关系就非常重要.如此才能在未来的空洞理论模型和真实的星系巡天中找出来的空洞之间建立起相关性.

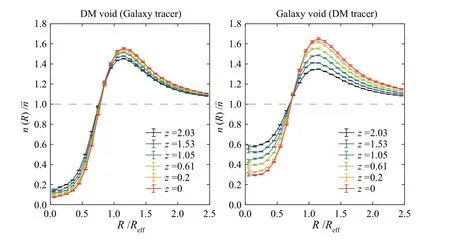
图10 交叉叠加密度轮廓的演化,左边是暗物质空洞,右边是星系空洞Fig.10 The distribution of cross stacked void density profile at different redshifts for DM voids(left panel)and galaxy voids(right panel)

5 结论

为了研究空洞的演化,我们在红移2.03到红移0之间取了6个红移位置的星系列表,同时为了考虑星系和暗物质两种示踪物找出来的空洞的统计性质偏袒以及他们在演化上的区别,我们还在对应红移处取了相应的暗物质粒子的数据,并且将其向下采样至与星系相同的数密度,从而去除粒子数密度不同带来的影响.由于星系数目随红移有变化,为了排除不同红移的星系数目不一致可能带来的问题,我们根据星系的数密度又产生了对应的具有相同粒子数密度的泊松样本.

我们使用VIDE程序得到空洞列表,但是我们在VIDE程序的第4步没有让密度场极小值区域向外扩展,我们的空洞列表由局域密度场极小值区域构成.我们研究了星系空洞和暗物质空洞的一些统计性质如大小分布、空洞数目、形状、叠加密度轮廓等随红移的演化,并且对比了星系空洞和暗物质空洞在演化上的异同以及星系空洞和暗物质空洞大小、数目、形状统计平均的比值随红移的演化.

使用密度场极小值区域作为空洞列表具有诸多优点.首先,能够避免人为设定的扩展条件带来的不确定性,这尤其在研究空洞的演化上具有很大的优势; 其次,在理论上密度场极小值区域更容易建模,可能是未来的一个很好的研究方向.

根据宇宙结构形成理论,由于引力的不稳定性,宇宙的原初物质密度涨落会随时间逐步增强,首先形成墙结构,进而塌缩成纤维结构及团块结构.在这一过程中,空洞的中心密度会持续降低,我们的工作和前人的结果都清楚地看到了这一效应.随着墙塌缩成纤维结构,墙上的低密区会出现缺口,引起相邻空洞贯通成为一个空洞,导致空洞数目减少,体积增大,形状变得更椭,我们的结果很好地反映了这一图景.我们的研究还发现,小的空洞倾向于处在高密度区域,这导致两个结果:(1)小空洞随高密环境一起塌缩,最终被挤压消失;(2)小空洞更容易与周围的空洞贯通成为大空洞,这两个效应都造成了小空洞的快速演化.我们的暗物质空洞的尺度演化统计结果很好地支持了这一预言.同时我们的结果也显示大尺度空洞特别是暗物质空洞有比较明显的增加,鉴于之前的研究表明,对于单个空洞而言,其膨胀压缩的演化非常缓慢,我们推断,低红移的大尺度空洞主要是由高红移的小空洞贯通而成的.

星系形成于高密度暗物质中,这造成了众所周知的星系和暗物质分布之间的偏袒,这一效应在空洞的统计性质上更加明显.由于星系主要示踪高密度区,不能有效示踪暗物质空洞的一些薄弱的墙结构,导致星系空洞表观上的提前贯通.在尺度方程和叠加密度轮廓上更加接近暗物质空洞的晚期分布形式.星系空洞受暗物质密度场的抑制,导致星系空洞之间的贯通效应不强,主要是被动演化,所以其大小、椭率、叠加密度轮廓等的演化都较暗物质示踪的空洞来得平缓.另外还需注意到,星系空洞和暗物质空洞(或者几个潜在的并合暗物质空洞)并不是严格一一对应的,先前的研究也发现它们的中心位置匹配得不好,这些因素都提醒我们在利用观测的星系空洞推断暗物质空洞属性时要特别谨慎.

以上的研究非常初步,有许多待完善的地方,一方面,目前在利用星系做示踪物找空洞的时候没有对星系进行质量加权,因此这部分问题带来的误差有待进一步澄清.另一方面,空洞的尺度和红移畸变的尺度相当,红移畸变会带来很大的影响[30–31].而实际观测数据总是在红移空间进行的,因此在研究示踪物的偏袒和空洞演化的时候还需要把红移畸变的影响考虑进来[72],这样才能够将模拟数据和真实观测数据进行对比.如前文所述,空洞具有很强的应用潜力,但同时目前还有很多细节需要澄清.

致谢感谢李国亮老师以及蔡彦川老师对本工作的指导和讨论.