基于非参数逆向思维的参数推断设计与模拟实验

吕书龙，刘文丽，梁飞豹，薛美玉

(福州大学 数学与计算机科学学院，福州 350108)

0 引 言

参数估计和假设检验是统计中最常见的两类统计推断问题，在点估计方面，矩估计法和极大似然估计法是基本方法，而区间估计和假设检验则通常是通过构造枢轴量[1-2]得以实现。随着非参数理论和方法的深入研究，各种基于非参数理论的统计推断方法也相继出现，如秩方法[2-3]、Bootstrap法[4-6]、随机加权法[7]等。关于分布参数的参数型和非参数型的统计推断方法的研究很多，成果也很丰硕，文献[8-16]中列举了近几年的一些研究。大量的研究成果极大地促进了经典的统计推断理论和方法的发展。

经典的参数统计推断问题的背景可描述为：假设总体X～F(x,θ)(或f(x,θ))，且F(x,θ)(或f(x,θ))的函数形式已知，但θ未知，θ∈Θ，其中Θ为θ的参数空间。已知该总体的一个样本X1,X2,…,Xn及其观测值x1,x2,…,xn，对于未知参数θ，经典的参数推断问题为：① 关于θ的点估计和置信度为1-α的区间估计；② 关于θ的假设检验问题。

现有的参数型或非参数型的很多方法都可以解决上述问题，其中有些方法都已成为教学和实际应用中的经典。在讲授“应用概率统计”和“统计计算”课程[1,17]的参数估计和假设检验内容时，为了激发学生对统计方法的探索和对R统计软件的应用水平，以密度函数、核估计、Bootstrap法3个关键词，要求构造一套基于直观统计理论和随机模拟的，有一定新意的统计推断方法。这个问题来自是教学过程中的一个突发的想法，本意是希望通过问题式、探究式教学来促进学生的统计计算思维。遗憾的是，这个综合了统计建模、实验设计、程序设计和随机模拟的问题没有在学生群体中得到突破，反而成了本文研究的一个起点。希望通过此文对类似课程的问题式、探究式、实验式教学提供一种参考，以便提升教学效果。

1 逆向法思路与模型构建

核密度是对总体密度函数f(x,θ)的一种估计实现，经验分布函数是对总体分布函数F(x,θ)的一种估计实现，不妨将这两个估计统一称为拟合分布，而F(x,θ)(或f(x,θ))统一称为理论分布。即

(1)

(2)

式中:h称为窗宽;K(x)称为核函数;I(x)为示性函数，当条件x为真时,其值为1,否则为0。现有的很多理论和实践都说明了上述估计的合理性和优良性[3-6,18-19]。

既然式(1)和(2)的非参数型拟合分布是理论分布的良好估计，那么在式(1)和(2)的基础上，不妨逆向思考：拟合分布Fn(x)(或fn,h(x))中形式上已经不含未知参数θ了，不妨转换其角色，将其当作最终的“理论分布”，而把含未知参数的理论分布F(x,θ)(或f(x,θ))当作“拟合分布”，然后通过合适的手段寻找最佳的θ,使得“拟合分布”逼近“理论分布”，这就诞生了求解未知参数点估计的一个方法，不妨称之为“非参数逆向思维法”。

此处合适的手段指构建度量“拟合分布”和“理论分布”偏差的损失函数，通过最优化手段确定某个θ的值使得损失函数值达到最小，得到未知参数θ的最优估计，即,

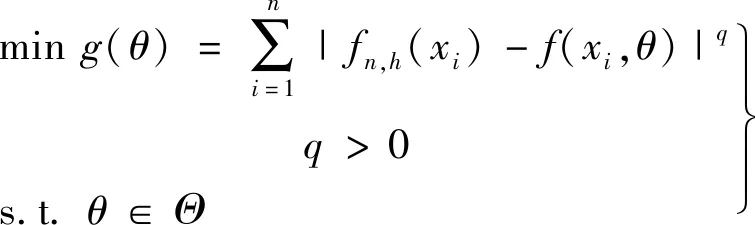
(3)

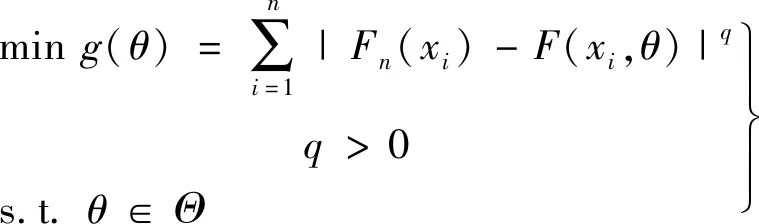
(4)

上述约束优化模型的求解若需要一个合理的初值，不妨取参数θ为参数空间Θ的中间值。

从形式上看，式(3)适用于连续型分布，若直接套用给离散型分布是不行的。实际上对于离散型分布，取其密度估计为频率即可，即

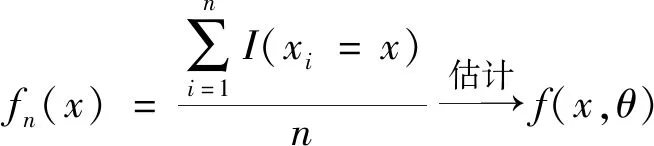
(5)

另外,若取函数K(x)=I(x)，且窗宽h=1，即可将式(5)统一到式(1)中。

式(3)和(4)给出了通过密度函数和分布函数求解未知参数点估计的基本模型，而要实现参数的区间估计与假设检验，还需借助非参数的Bootstrap方法。利用Bootstrap理论和方法，以已知样本产生足够多的自助样本并利用式(3)或(4)得到相应的θ估计序列，再基于Bootstrap方法体系中的求解区间估计的枢轴量和非枢轴量法[5]，可计算出未知参数θ的置信度为1-α的区间估计，同理可计算未知参数θ相应的假设检验问题的检验p值。

2 逆向法解决3个核心问题的过程设计

2.1 点估计的实现

考虑式(3)或(4)中的q值，若取q=2，则是基于最小二乘思想；若取q=1，则基于最小一乘思想，代入样本观测值，可得到θ的点估计。结合R软件给出如下过程：

步骤1根据样本选择合适的窗宽h，由式(1)结合R软件中的density函数得到核密度估计fn,h(x)或者由式(2)结合R软件中的ecdf函数是得到经验分布函数Fn(x)。

步骤2选定q值，构建式(3)或(4)的最优化目标函数g(θ)。

若希望得到未知参数θ更稳定可靠的估计，可以引入Bootstrap方法，以Bootstrap法估计的平均值作为最终的点估计值。

2.2 区间估计的实现

近似正态法：由

可得：

(6)

近似t分布法：由

可得：

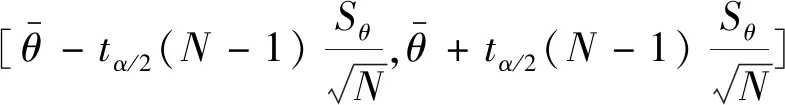
(7)

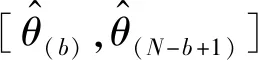
(8)

2.3 检验p值的实现

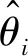
近似正态法：

(9)

此处Φ(x)为标准正态分布的分布函数。同理可以实现近似t分布法的检验p值，不再赘述。

分位数法：

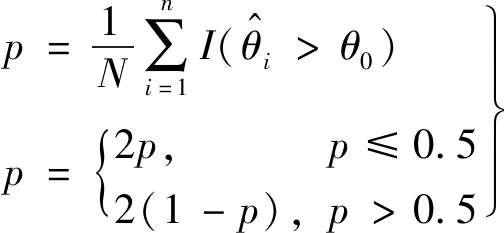
(10)

参照双侧检验的作法，同理可以得到右侧检验或左侧检验的检验p值。

3 逆向法的随机实验设计与分析

例1设样本X1,X2,…,Xn及观测值x1,x2,…,xn来自柯西分布总体X～C(μ,γ)，其概率密度函数为

求参数μ、γ的估计值。

柯西分布的各阶矩均不存在，故无法使用矩法得到点估计，但可以使用极大似然估计法。而本文方法属于非参数法，故不受此限制。下面给出本文方法(简称逆向法)和极大似然估计法(简称极大法)的随机模拟比较结果。

从表1结果可知，式(3)和(4)定义的逆向法可用来求解分布参数的点估计。由于核密度估计受到窗宽的影响较大，故式(3)的逆向法与极大似然估计法的偏差较式(4)的逆向法大，而式(4)的逆向法与极大似然法估计的结果非常接近。再给出μ=0,γ=1时，100次模拟的各种基本统计指标，以便比较这3种估计，具体见表2。

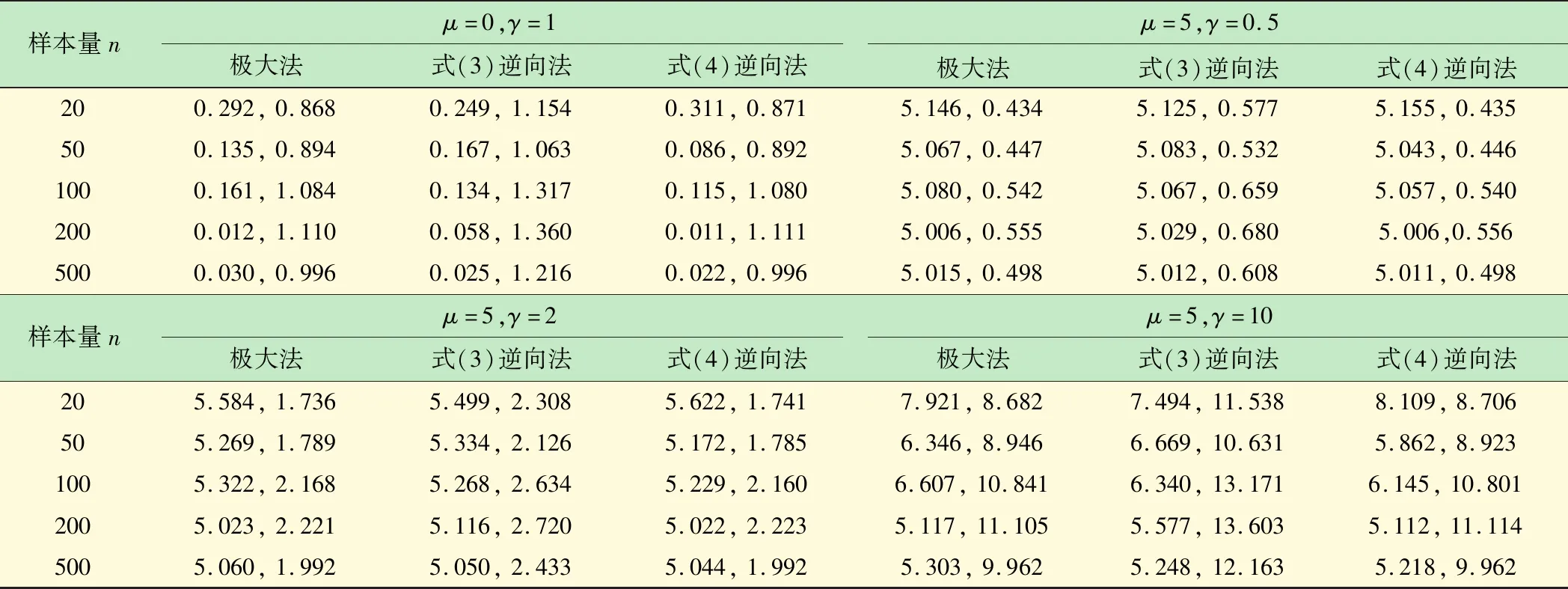
表1 逆向方法与极大似然估计法对于参数μ和γ估计的模拟对比(q=2)

注：模拟用的随机样本采用函数set.seed(12)进行固定以便分析结果可验证和可重现，具体程序见附录1

表2 2个参数(μ,γ)100次随机模拟估计值的统计指标(q=2)

注：具体程序见附录2

从表2及图1、2输出可知，式(3)逆向法的各项统计指标弱于式(4)逆向法，且式(3)逆向法与极大似然估计有较大差异。但式(4)逆向法与极大似然估计法只有微小差异，由检验p值可知，两者不存在统计意义上的显著差异。

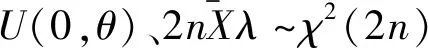
对表3给出的计算结果分析可知，式(4)逆向法结合Bootstrap方法得到的区间估计与检验p值与常规的方法相比没有本质区别，这归功于经验分布函数的稳健性。而式(3)逆向法得到的区间估计与检验p值与常规方法相比大部分没本质区别，但在指数分布上差异明显，主要原因在于指数分布的密度最高值在边界处达到，而核密度估计的劣势正好在边界处。但在分布密度基本对称时，式(3)和(4)没有本质差异。

图1 参数μ的100次模拟结果的箱线图

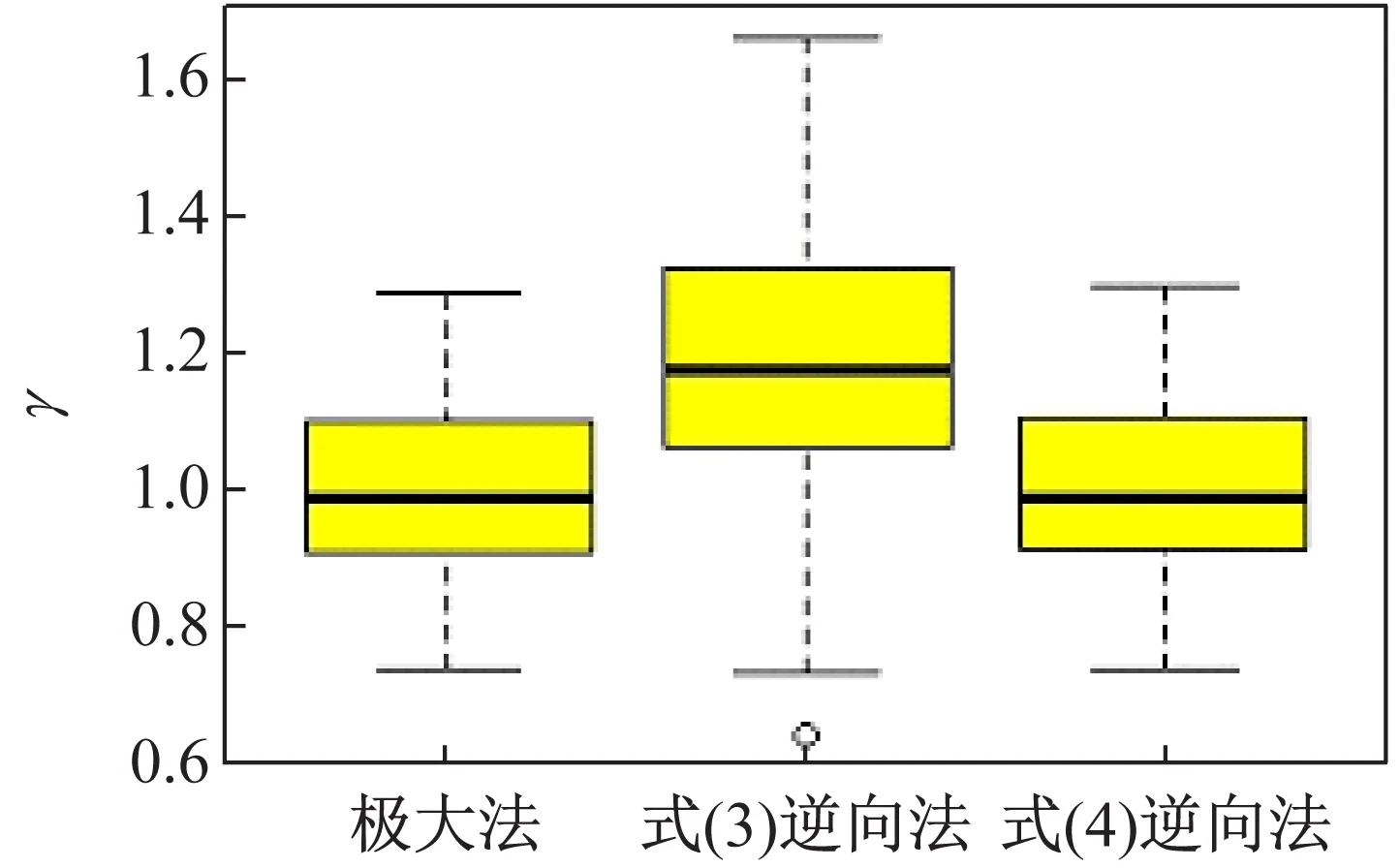
图2 参数γ的100次模拟结果的箱线图

表3 分布参数的双侧置信区间和检验p值(q=2)

注:各分布均采用函数set.seed(12)指定随机数表，分别提取100个随机数；Bootstrap方法的自助样本依随机数表1～2 000生成，见附录3

总体而言，在实际应用中，式(4)逆向法优于式(3)逆向法。一方面式(4)逆向法估计精度有保障而且估计更稳健；另一方面式(4)逆向法的计算效率高于式(3)逆向法。

4 结 语

本文将非参数核密度估计和经验分布函数这两个实际上的拟合分布当作“理论分布”，而将密度函数和分布函数这两个实际上的理论分布当作“拟合分布”，让“拟合分布”逼近“理论分布”为基本思想逆向地构建了两者之间逼近的损失函数，通过优化模型得到未知参数的估计，并给出了这两套方法的R脚本程序。通过构建两个例子和大量的随机模拟过程，一方面将这两套方法与极大似然估计方法进行比较;另一方面给出了解决统计推断中的区间估计和假设检验两类问题的基本过程，实现了统计方法教学所需要的完整过程，有利于学生充分思考、研究并掌握该方法，随机模拟实验设计与对应的R程序也便于实际教学及演示。随机模拟结果表明基于分布函数的逆向法的普适性、精确性和稳健性优于基于密度函数的逆向法，基于分布函数的逆向法与极大似然估计方法没有本质差别。在区间估计和假设检验方面，基于分布函数的逆向法表现与常规方法无显著差异；除了在边界处出现密度极端值外，其他情况下，基于密度函数的逆向法与常规方法也没有太多差别。但在实际应用中，建议优先使用基于分布函数的逆向法。至于如何提高基于密度函数的逆向法的普适性，则需要在核密度估计的天生缺陷问题上进行改进，有一定难度。至于提高基于密度的逆向法的精度，需要样本量、最优窗宽和核函数的综合考量，有待进一步研究。