四旋翼飞行器动态粒子群优化算法的PID控制技术

胡文华，曹仁赢，温泽之，刘剑锋

(华东交通大学 电气与自动化工程学院，南昌 330013)

0 引 言

得益于传感器、微处理器、通信以及新材料等技术领域的飞速发展，并应用于四旋翼飞行器上，使四旋翼飞行器具有体积小、灵活度高、结构简单、性能可靠的特点，现已在各行各业得到深入的应用。例如农业领域：无人机农作物监测、数据采集，无人机农药喷洒除害；能源领域：输电线路无人机巡检[1]，石油和天然气管道设备检测；公共安全领域：在突发事件中，无人机可大范围监控和搜索，迅速传递现场情况；媒体领域：采用无人机摄影，为记者、摄影师提够独特的视角；军事领域：无人机参与战场勘察、火力支援、目标跟踪等；除此之外，无人机还在环境评估、交通调控、基础设施建设、物流、家庭娱乐方面有着广泛的应用。在此背景下，研发具有高可靠性、高精度、控制迅速的四旋翼飞行器控制系统是工业界和学术界都广泛关注的课题。

PID控制[2-4]技术是工业生产过程中应用最广，也是最成熟的控制技术。对于线性系统，PID控制能达到较好的控制品质且参数整定难度小、计算量不大。然而，对于欠驱动、强耦合、非线性、多变量的四旋翼飞行器，采用常规的PID参数整定方法则计算量复杂，不能获得最优的控制参数，难以满足飞行器设计需求。由此，在实际工程中往往采用各种改进PID[5-7]控制技术，其中就有基于粒子群优化(PSO)算法的PID控制技术，然而对于四旋翼飞行器的复杂控制系统以标准PSO算法改进的控制技术存在陷入局部最优和收敛速度慢的问题。

本文采用动态粒子群算法设计四旋翼飞行器的PID控制器。该方法既有标准PSO不需要人工调整参数，粒子群自动寻优的优点，又有效避免了标准PSO会陷入局部最优的缺点以及为避免陷入局部最优增加粒子群数量和迭代次数，导致收敛速度慢与计算量大的问题。

1 四旋翼飞行器建模

通过四旋翼飞行器的动力学[8]与运动学方程以及欧拉定理建立了四旋翼飞行器的数学模型[9-10]：

(1)

式中:x、y、z为四轴飞行器地理坐标系下的空间坐标系的坐标位置；φ、θ、ψ分别是机体相对于参考坐标系(地理坐标系)的翻滚角、俯仰角、偏航角；Ix、Iy、Iz分别为飞行器绕x、y、z轴的3个转动惯量；g为飞行器所受重力加速度；m为飞行器整机质量；u1、u2、u3、u4为系统控制量，它与4个旋翼的转速关系如下：

(2)

式中:kt表示飞行器旋翼的升力系数;kd表示飞行阻力系数;Ω1、Ω2、Ω3、Ω4分别表示飞行器无刷直流电动机[11]调控的4个旋翼转速。

2 动态粒子群算法

2.1 标准粒子群算法

PSO是计算智能领域除了遗传算法[12]、蚁群算法[13]、鱼群算法[14]之外的一种群体智能优化算法[15]。PSO中的每个粒子都有n个维度，代表所需解决问题的一组可能解，通过与其他粒子相互作用以及适应度函数不断更新自身，以及整个群体的状态信息从而找到问题的最优解。

假设在n维空间中，粒子群由m个粒子组成，Xi=(xi1,xi2,…,xin)表示第i个粒子在n维空间的位置，也即一组潜在解；vi=(vi1,vi2,…,vin)表示第i个粒子的速度；Pi=(pi1,pi2,…,pin)表示第i个粒子在迭代过程中保留的历史最优值；Pg=(pg1,pg2,…,pgn)表示整个粒子群的历史最优值。

粒子群中的每个粒子在迭代过程中通过自身历史最优值和群体最优值按下式更新自身在空间中的速度和位置:

(3)

(4)

式中:ω为惯性权重；d=1,2,…,n；i=1,2,…,m；c1、c2为加速度因子，其值大于零；r1、r2是分布于[0，1]区间上的随机数；k为当前迭代的次数。为避免粒子群在解空间内盲目搜索，通常会设置粒子位置和速度的上限和下限。

ω体现了粒子继承先前速度的能力，Shi提出了线性递减惯性权重，

ω(k)=ωmax-k(ωmax-ωmin)/Tmax

(5)

式中:Tmax为最大迭代次数;ωmax、ωmin分别为最大和最小的惯性权重值。较大的惯性权重值有利于全局搜索，而较小的惯性权值则更有利于局部搜索。

2.2 惯性权重的改进策略

通过分析式(5)可知，迭代过程中ω呈线性递减，初期惯性权重值大，全局搜索能力强，符合早期需要粒子探索能力的要求，而后期惯性权重值小，有利于粒子收敛于全局最优值。但这样的方法存在一定的问题。① 若粒子群前期就搜寻到较优点，则希望粒子快速收敛于全局最优点，但初期惯性权重值ω较大，减慢了粒子的收敛速度；② 迭代后期，因为ω逐渐减小，使得全局搜索的能力降低，粒子群缺乏多样性，易陷入局部最优。

通过分析式(3)可知，越靠近最优解的粒子，其式(3)右边后两项越趋近于零，其速度越取决于ω。综上,提出改进惯性权重策略的方法：让靠近最优点附近的部分粒子在最优点周围搜索，而不承担大范围的搜索，赋予其较小的ω，而让远离最优值的粒子承担大范围的搜索，赋予其较大的ω，因此ω的值不仅会随着迭代次数变化，而且会因为不同粒子与最优值之间距离远近的改变而发生变化。故设计思路是：一方面粒子ω会随着迭代次数增加而减少;另一方面ω会因为粒子与全局最优点距离远近而动态变化[16]。

设Lki表示第k次迭代后粒子i与当前最优粒子的距离(全局最优粒子除外);Lkimax表示粒子i经过k次迭代后的最大Lki;Lkimin表示粒子i经过k次迭代后的最小Lki，则有：

ω随距离大小的关系

(6)

ω随迭代次数而递减的关系

(7)

式中,Tmax为最大迭代次数。

结合上述两种因素，由式(6)和(7)可得：

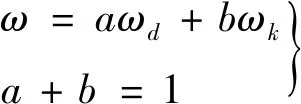
(8)

式中,a、b为常数，a可取0.45。

2.3 粒子杂交

由于惯性权重的引入，在迭代次数逐渐增长的过程中，最优粒子的控制度会不断得到强化，使得整个粒子群多样性逐渐下降，容易陷入局部最优。故引入杂交变异，在连续h代迭代过程中，若全局最优点一直未变化，表明粒子群很可能陷入了局部最优。为使种群多样性提高，此时可从m个粒子中选取较优的q个粒子(包括最优粒子)的历史最优位置，与新产生的粒子随机杂交，从而改变最优粒子的前进方向和速度，以进入其他区域搜索，寻找新的个体极值，

Pnew(xi)=cPselect(xi)+(1-c)Pcurrent(xi)

(9)

式中：Pnew为新产生的粒子;Pselect为选取的较优粒子；Pcurrent为当代新产生的粒子;c为[0，1]之间的随机变量。

2.4 动态粒子群算法的基本流程

(1)初始化粒子群各个粒子的位置和速度，根据适应度函数值选择粒子个体历史最优和全局最优；

(2)计算各个粒子与当前全局最优位置的距离，得到Lkimax，Lkimin,由式(8)更新下次迭代各粒子的ω；

(3)根据式(3)、(4)更新每个粒子的位置和速度并计算适应度值；

(4)若该粒子当前适应度值比其历史最优值好，则当前值取代历史最优值；

(5)若该粒子历史最优值比全局最优值好，则替代全局最优值；

(6)判断是否满足杂交条件即连续h代全局最优值保持不变，是则执行第(7)步，否则执行第(8)步；

(7)从m个粒子中选取q个较优粒子根据式(9)杂交产生新粒子，替换旧粒子，再执行第(2)步；

(8)判断是否满足终止条件，是则输出全局最优点，否则执行第(2)步。

3 动态粒子群算法PID控制器

(1)根据四旋翼飞行器的数学模型，在MATLAB/Simulink中搭建四旋翼飞行器仿真模型，如图1所示(以四旋翼飞行器高度和3个姿态角控制为例)。

图1 四旋翼飞行器仿真模型

(2)在MATLAB中编写动态粒子群算法程序代码，通过Rastrigrin测试函数重复运算，结果如图2所示，证明了其算法的准确性。

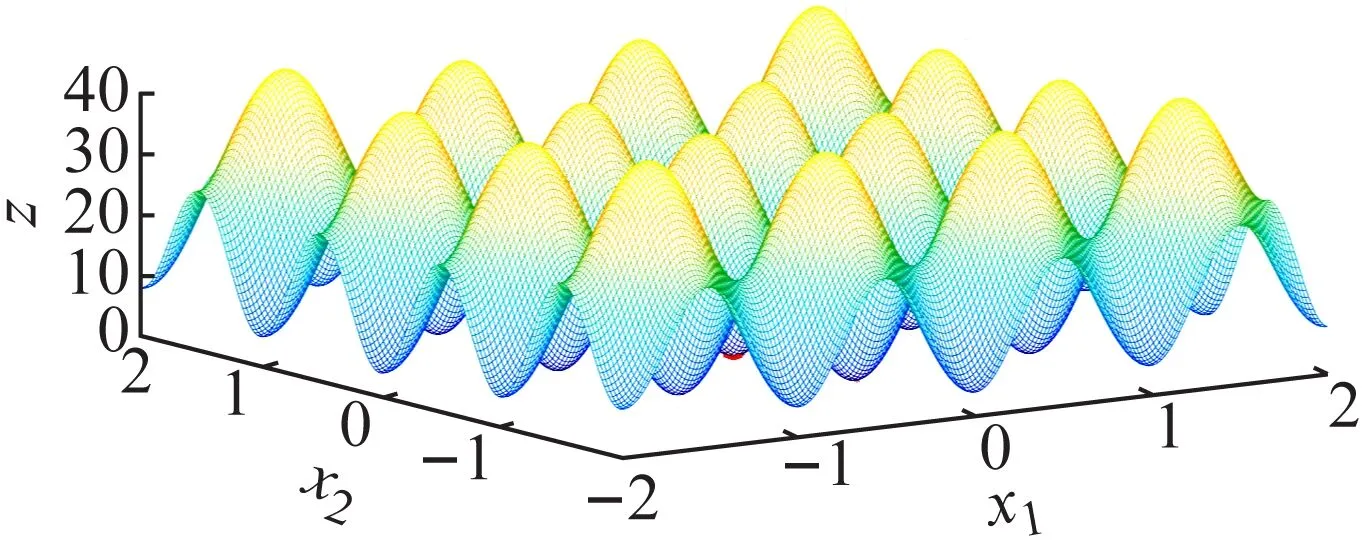
图2 Rastrigrin测试函数

将其与四旋翼飞行器仿真模型中的PID控制器相结合，如图3所示。图中误差性能指标定义为：

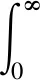
(10)

(3)设置四旋翼飞行器参数和动态粒子群算法初始化参数。四旋翼飞行器参数如下：m=0.75 kg，l=0.25 m，Ix=19.68 g·m2，Iy=19.68 g·m2，Iz=3.93 g·m2。

图3 动态粒子群算法PID控制器

动态粒子群算法初始化参数如下：维度=3，ωmax=0.9,ωmin=0.4,c1、c2=2,粒子群规模=50,迭代次数=50，粒子速度范围=[-1，1]，Kp、Ki、Kd=[0，50],最小适宜度值=0.01。

(4)仿真结果分析。以高度为例，设置了悬停高度为4 m。高度变化曲线如图4所示。

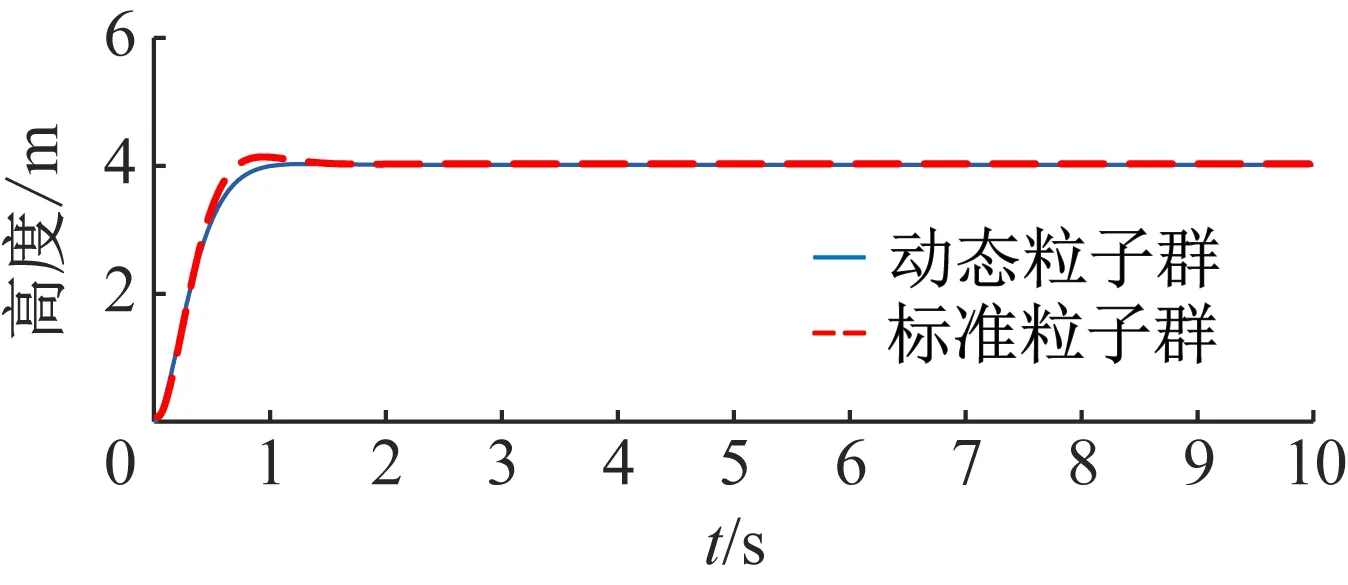
图4 高度变化曲线

迭代次数误差适应度值变化曲线如图5所示。

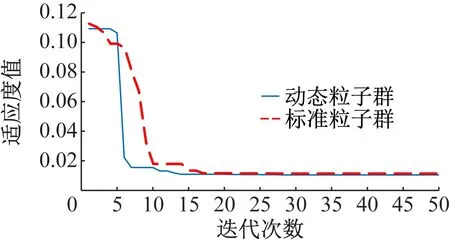
图5 误差适应度值变化曲线

采用动态PSO，Kp、Ki、Kd参数优化随迭代次数变化如图6所示，标准PSOKp、Ki、Kd参数变化如图7所示。

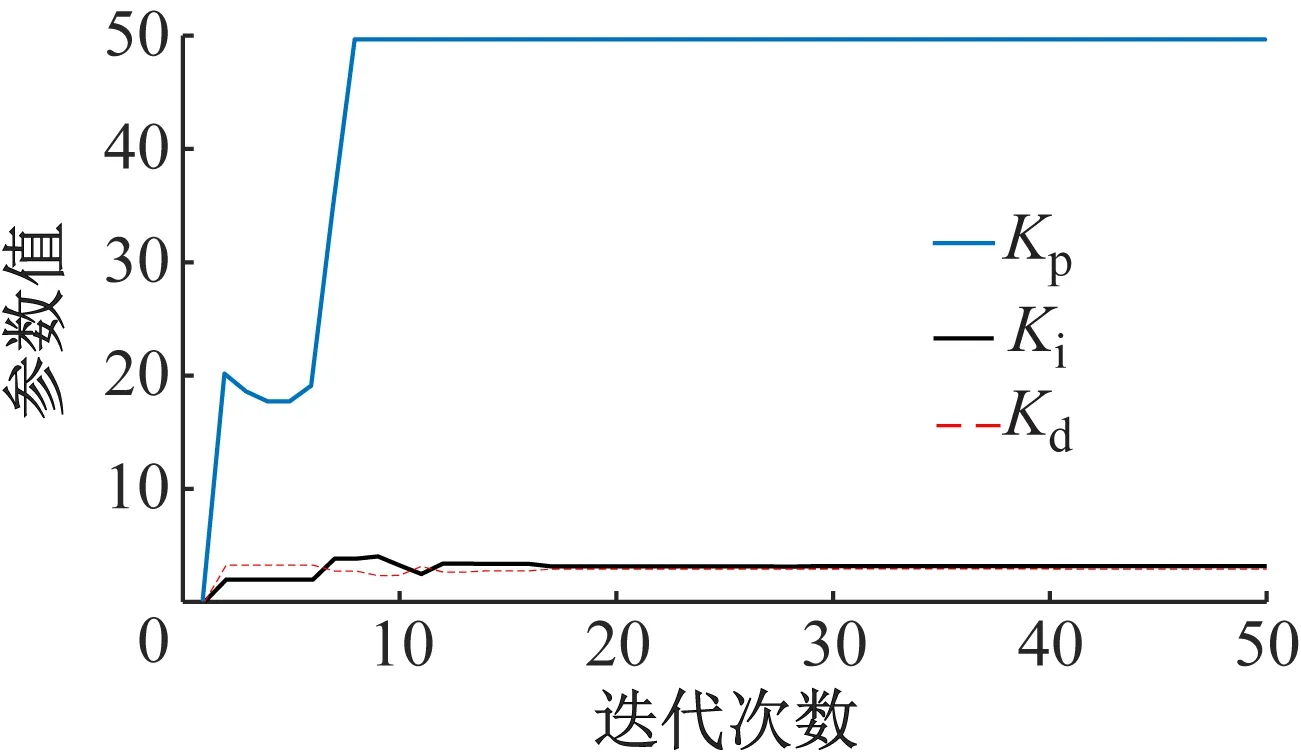
图6 动态粒子群Kp、Ki、Kd优化曲线

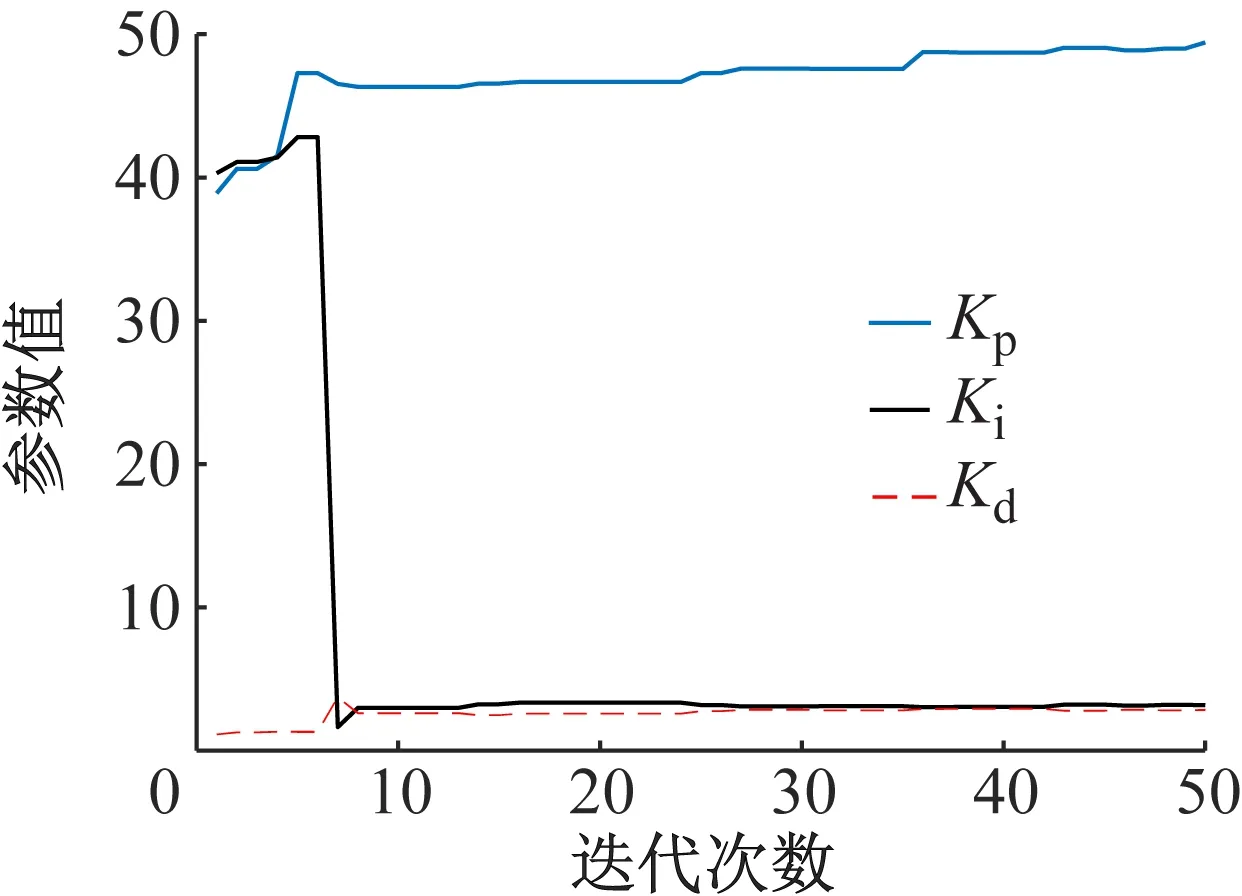
图7 标准粒子群Kp、Ki、Kd优化曲线

由图4～7仿真结果证明,动态粒子群算法相比于标准粒子群算法，其对四旋翼飞行器高度控制不仅超调量更小，控制更精确，而且收敛速度更快，对于实际复杂飞行控制系统它的控制将更迅速，更有效率。

4 结 语

本文在对标准PSO研究的基础上，对PSO进行改进优化，用以对四旋翼飞行器的飞行姿态和位置进行控制，通过Simulink搭建飞行器仿真模型，证明了基于动态PSO的PID控制技术能更好的避免陷入局部最优，实现更精准控制，同时其收敛速度更快，提高了飞行控制系统设计的效率，对以后用于更复杂的飞行器模型或需要对更多参数整定的控制方法具有重要的参考价值。