不同土岩比地表沉陷特征数值模拟分析

叶帅飞，王 辉，杨修歌

（河南理工大学土木工程学院，河南 焦作454000）

0 引言

中国是世界上煤炭资源最丰富的国家之一，已经探明的总储量位居世界前列，同时我国也是煤炭使用大国，煤炭作为我国的主要能源，对我国的经济发展起着举足轻重的作用，因此大量煤炭的开采也是必然的.我国的煤炭资源广泛分布在平原、丘陵、山地等地区，地形的复杂使得煤炭的开采面临着很多问题.对于一般地层结构条件下的开采，地下矿产的开采造成上覆岩体及地表的移动规律，经过大量的研究和探索，已经有了较为成熟的研究成果.但是地表移动变形观测资料分析表明，不同的松散层厚度与不同的基岩厚度条件下的开采，造成的地表移动规律有一定的特殊性，因此不同松散层厚度和基岩厚度条件下的开采研究不能等同于一般开采条件下的研究，一般的开采沉陷理论也不能适用于土岩比变化比较大的条件下的开采.近年来，许多数学者对厚松散层条件下开采的地表移动规律进行了研究，取得了大量的成果，但对于土岩比变化较大情况下的开采造成的地表移动规律的认识尚不充分，有待继续研究[1-3].

1 厚松散层和薄基岩的定义

在煤层开采中，松散层与基岩的厚薄以及土岩比都对煤层开采的沉陷参数、地表下沉和岩层移动有着很大的的影响.但是目前对于厚松散层与薄基岩的定量还没有任何的资料给予明确的界定[4].

参考大部分文献和资料认为松散层可以分为薄松散层、厚松散层和巨厚松散层，综合分析后给出了建设性的定量界定：厚度小于50 m的松散层称为薄松散层；厚度大于50 m小于100 m的松散层称为厚松散层；厚度大于100 m的松散层则被称为巨厚松散层.而对于薄基岩的定义也未见相关的资料给予确切的定量，这里以煤层开采后引起的煤层上方“三带”即垮落带、断裂带、弯曲带与基岩厚度的相对关系来确定薄基岩建设性的定量界定：当基岩厚度小于垮落带高度时，称为超薄基岩；当基岩厚度大于垮落带高度小于断裂带高度的时候，称为薄基岩；当基岩厚度大于断裂带高度时，称为正常厚度基岩.假设垮落带的高度可以填满整个采空区，则垮落带的高度可以取采高的2～4倍；而断裂带的高度可以取采高的4～8倍[5-6].

2 不同土岩比地表变形沉陷分析

2.1 不同松散层厚度下的沉陷模拟分析

为了研究不同厚度松散层下的沉陷规律，将采用FLAC3D软件进行模拟.在岩层厚度不变的情况下，改变上部松散层的厚度，模拟得到的地表变形规律是不相同的.因此现将模型的岩层厚度固定，分阶段的递增上部松散层的厚度，以获得地表的沉陷规律.

同时为提高计算精度，使模拟结果更加准确，因此建立模型前需确定模型的物理力学参数、选择地层的本构模型及确定模型的边界条件[7].模拟采用西部某矿区的各类岩层物理力学参数，详细参数如表1.在FLAC3D中摩尔-库伦本构模型被广泛应用到岩土体工程的模拟运算中，针对本工程选用摩尔-库伦本构模型能够提高运算速度，使收敛时间缩短，因此各类岩土体将采用库伦-摩尔本构模型进行运算[8-10].根据现场勘查岩层

应力主要以自重应力为主，因此模型中上部地表为自由面无加载，模型的主要受力为各地层的自重应力，模型底部为固定约束，四周采用位移约束.

表1 各类岩层物理力学参数表

该模型以该矿区一个采煤工作面倾向剖面作为建立物理模型的基础.在建立模型的过程中为了能够针对某一问题进行解决，不需要把所有情况都考虑进去，因此做出以下假定：认为各地层都是均匀连续的，不考虑周围其他采空区对该处的影响.对此在建立模型时为了计算方便对地层和模型尺寸进行了相应的简化处理.开采厚度为1 m，模型截面大小为80 m*80 m，采空区走向长度为30 m，倾向长度也为30 m.现固定岩层厚度为30 m，松散层厚度为20 m～140 m，以10 m为步长逐级增加松散层的厚度进行模拟计算.计算模型如图1.

图1 计算模型图

在松散层厚度不同的情况下，以地表监测点位置为横坐标绘制下沉曲线图和地表位移曲线图，如图2和图3.

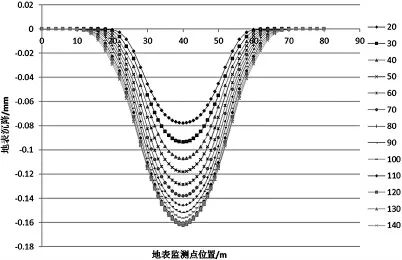
图2 地表下沉与松散层厚度关系曲线图

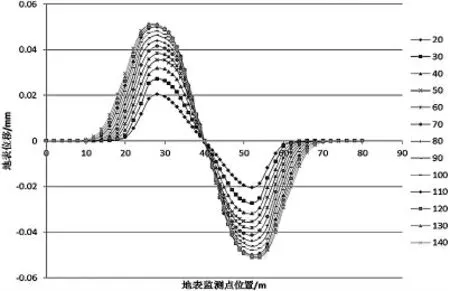
图3 地表位移与松散层厚度关系曲线图

由图2、图3以及模拟出的随松散层厚度改变时的位移和沉降云图可以看出，其下沉曲线基本符合倒概率分布曲线的形式，且关于采空区中间对称.当上覆岩层厚度一定时，随着松散层厚度的改变，地表的影响范围在逐步的扩大，最大下沉值也在逐步增加，其下沉率也变得越来越大.对于地表位移曲线，伴随着松散层厚度的增加，位移的最大值的位置处于开采工作面的边缘部位，并且基本不变.而在盆地边缘部位指向采空区中心位置的位移量在大幅度的增加，位移率也在不断增加.地表的最大沉降位于采空区中心位置，水平移动曲线呈现中心反对称的形式.

取松散层厚度不同时地表的最大位移量和最大沉降量，绘制出如图4和图5的曲线，根据图中曲线形式，在基岩厚度不变时改变松散层厚度有如下规律：

（1）随着松散层厚度的增加，最大沉降和最大位移曲线都呈现出对数曲线的形式，其最大沉降量和最大位移量的增长逐渐变缓，最终趋于平稳.

（2）随着松散层厚度的增加，地表下沉等值线逐渐变缓，下沉盆地的坡度明显变缓，采空区引起的地表垂直方向的位移影响范围明显变大.

（3）随着松散层厚度的增加，地表水平方向的位移影响范围逐渐扩大.

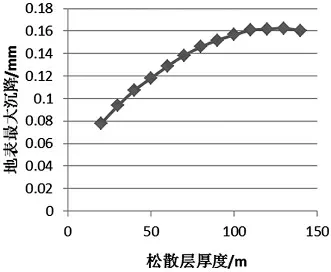
图4 最大下沉值与松散层厚度关系曲线

图5 最大位移值与松散层厚度关系曲线

地表沉降和位移等值云图，如图6 和图7 所示.

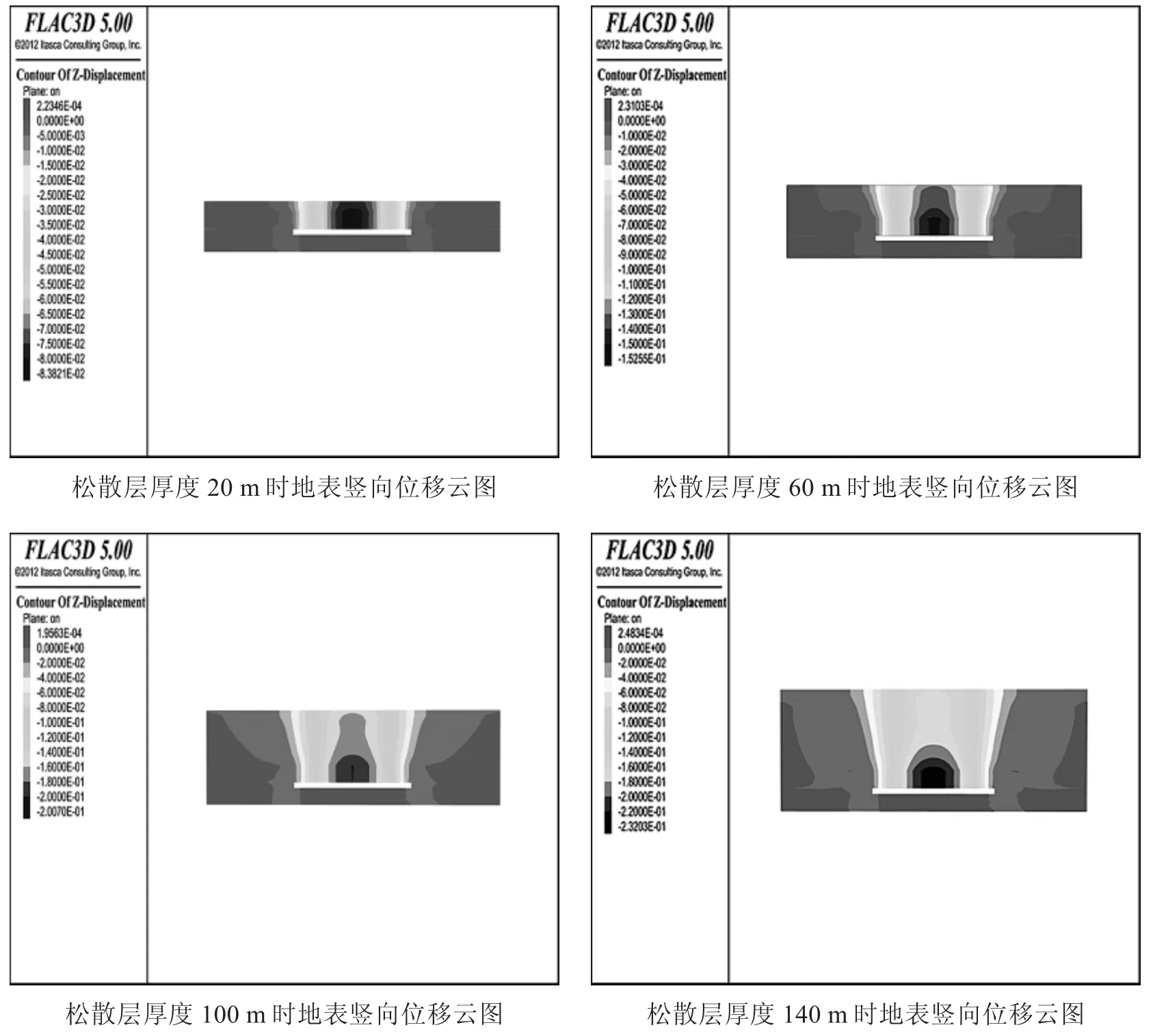
图6 不同松散层厚度地表竖向位移云图

图7 不同松散层厚度时地表水平位移云图

当控制岩层厚度改变松散层厚度时，通过对数值模拟结果分析得到如下结论：

（1）随着松散层厚度的改变，其地表移动变形分布规律与一般条件下的开采所引起的地表移动变形规律基本相同.地表最大下沉值位于采空区中心，地表下沉曲线关于采空区中心对称，最大下沉值随着松散层厚度的增加有增大的趋势.地表位移曲线关于采空区中心成反对称关系.

（2）当岩层厚度不发生改变的时候，松散层厚度由20 m 开始以20 m 为步距增加到140 m 时，地表最大沉降值呈现出对数曲线增长的方式.最大下沉值由80 mm 增加到160 mm，在松散层厚度达到110 m 时最大下沉值就达到了160 mm，若继续增加松散层的厚度，其地表最大下沉值基本稳定不变.而大于100 m 的松散层为巨厚松散层，因此当松散层厚度达到巨厚松散层时，其地表最大下沉值呈线性趋势，基本稳定在某一数值.

（3）地表位移曲线随着松散层厚度的增加其形式基本不变，最大位移值位于开采区域的边界处.开采区域以内的地表随松散层厚度的增加，位移增大趋势不明显，但是在开采区域以外的地表其位移增大趋势比较明显.

（4）地表位移最大值随着松散层厚度的增加呈现对数曲线关系，在松散层厚度达到110 m 时候，地表位移达到最大值.当松散层厚度继续增加，即岩层上方为巨厚松散层时，其地表最大位移值维持在一数值基本不变.

（5）随着松散层厚度的增加，地表下沉更加明显.开采对地表造成的影响范围明显的扩大，在整个采空区域内地表的沉降曲线收敛越来越缓慢，曲线的分布形式也由较陡变得缓和一些.

2.2 不同基岩厚度下的沉陷模拟分析

当固定松散层厚度，改变岩层厚度时，地表移动变形规律也是不尽相同的.因此固定松散层厚度，通过改变岩层厚度进行模拟计算，以此得到岩层厚度对于地表移动变形的影响.

为了研究不同岩层厚度对于地表移动变形的影响，基于大型数值模拟软件FLAC3D建立数值模型.模型尺寸为80 m*80 m，开采区域的走向长度和倾向长度都为30 m.上部松散层厚度固定为40 m，岩层厚度由40 m 到130 m，以10 m 为步距逐渐增加进行计算研究.

固定上部松散层的厚度，通过改变下部岩层厚度进行模拟计算，将得到的计算结果以地表监测点位置为横坐标绘制不同岩层厚度下的地表沉降和位移图，如图8 和9.以岩层厚度为横坐标，不同岩层厚度下的地表最大位移量和最大沉降量为纵坐标绘制出如图10 和11 的曲线图.

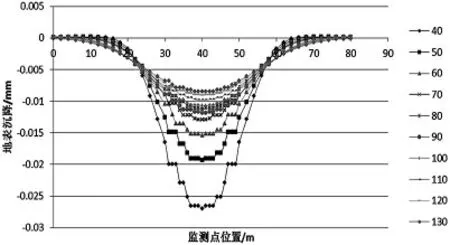
图8 地表沉降与岩层厚度关系曲线图

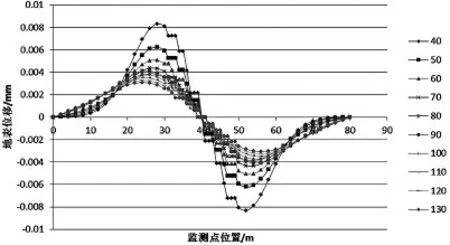
图9 地表位移与岩层厚度关系曲线图

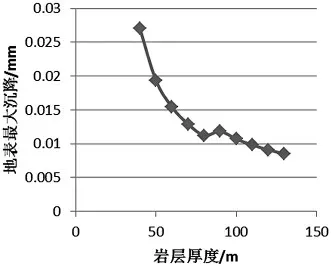
图10 最大下沉值与岩层厚度关系曲线

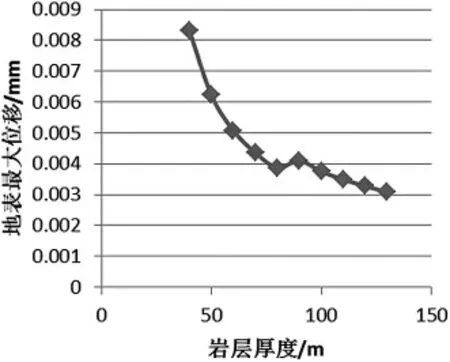
图11 最大位移值与岩层厚度关系曲线

由图8 可以看出地表下沉曲线关于采空区中心对称，随着岩层厚度的增加，中心最大沉降量越来越小，而采空区对地表的影响范围在逐步的扩大，同时地表的沉降速率在不断地减小，地表也变得更加平缓.由图9 可以发现地表位移曲线图关于采空区中心成反对称，随着岩层厚度的增加，位移影响范围在不断扩大，地表位移最大值出现在采空区的边界处.最大沉降值出现在采空区的中心.

从绘制的最大沉降、位移值与岩层厚度关系曲线上可以看出，随着岩层厚度的增加其最大位移值与最大沉降值都在逐渐减小，呈现负指数函数曲线的形状.两曲线随着岩层厚度的增加变得越来越平缓，其最大值的减小速率也随之减小.在岩层厚度为90 m 的时候其最大位移与沉降值出现了小浮的上涨，说明了岩层厚度对地表的沉降位移起到了控制作用.随着岩层厚度的增加，地表沉降位移量也在不断减小，这也说明了岩层的控制作用.

岩层厚度对地表位移与沉降影响的等值云图如图12 和图13.

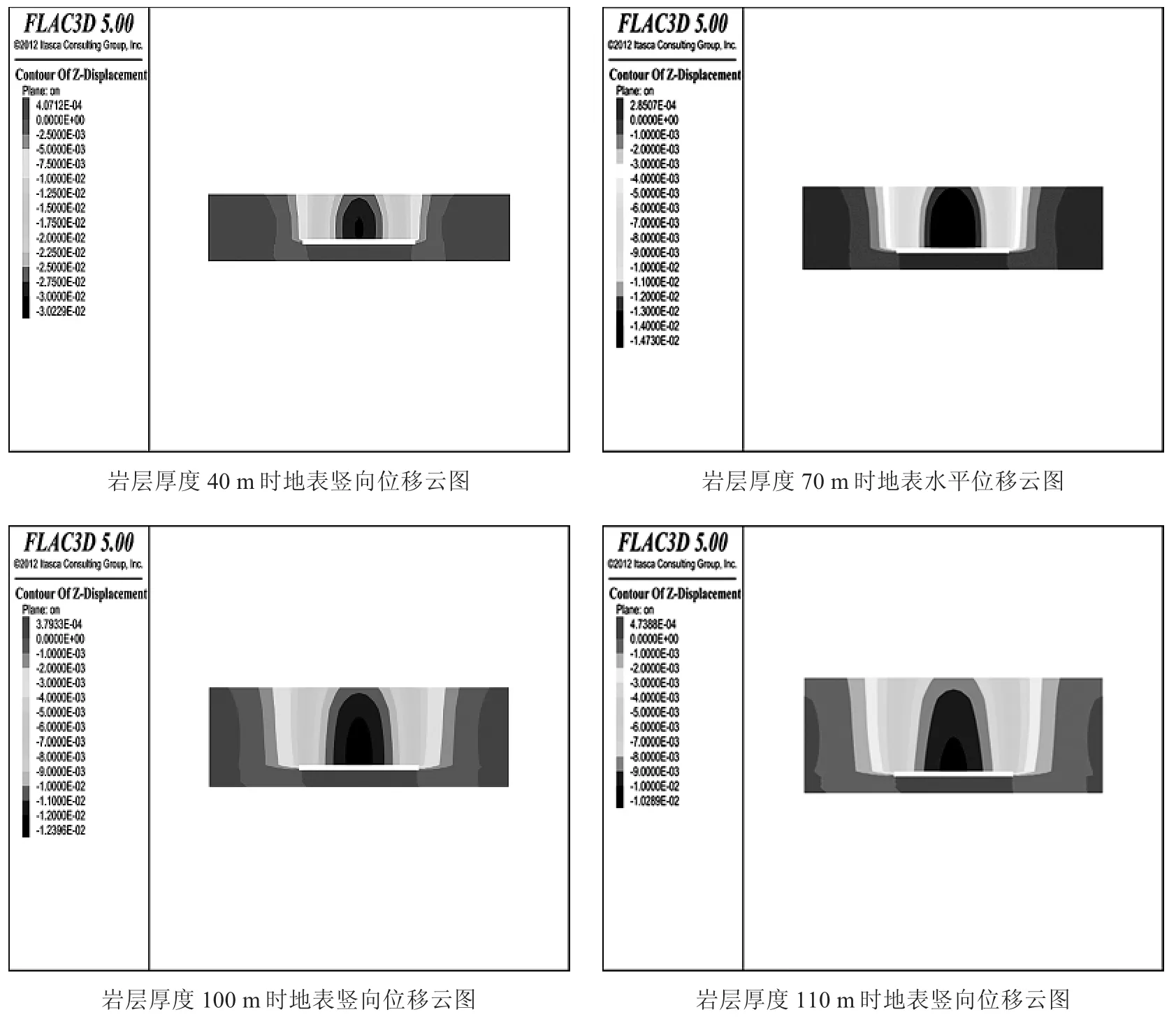
图12 岩层厚度不同时地表竖向位移云图

图13 岩层厚度不同时地表水平位移云图

通过对不同岩层厚度下地表变形规律的模拟研究，得到如下结论：

（1）固定松散层厚度，基岩厚度由40 m 逐渐增加到130 m 的过程中，地表下沉与位移的最大值在不断地减小，地表的下沉与位移速率也在不断减小，地表变形更加的缓和.说明了随着基岩厚度的增加，控制松散层沉降变形的岩层也在增加.充分说明了岩层的控制作用.

（2）随着基岩厚度的增加，地表位移的最大值逐渐减小，地表沉降的最大值也逐渐减小，最大位移值位于采空区边缘附近，最大沉降值位于采空区的中心.地表位移最大值逐渐减小的同时，地表位移范围有逐渐扩展的趋势，且扩展的趋势没有下沉曲线明显，但是在位移的边缘附近随着基岩厚度的增加位移值也在不断地增加.

2.3 计算结果对比分析

该矿区为厚松散层薄基岩型地层，与固定基岩厚度松散层厚度为130 m 的模拟地层情况相对应，将模拟结果与实测结果进行对比分析，如表2.

表2 对比分析表

模拟值与实测值相差并不大，说明模拟结果的正确性，也说明了运用FLAC3D进行模拟计算该问题是可行的.

3 结论

以西部某矿区的岩层参数为基础，以不同的土岩比为条件进行数值模拟分析，对得出的不同土岩比条件下数值模拟结果进行分析表明：

（1）固定岩层厚度，随着松散层厚度的增加，地表沉降和位移影响范围在不断扩大，沉降中心地区变得越来越平缓，最大沉降值与最大位移值先成对数曲线增长，然后呈线性趋势且稳定在某一数值范围内.最大沉降速率和最大位移值出现在开采工作面边缘处，在盆地边缘部位指向采空区中心位置的位移量在大幅增加，位移率也在不断增加，整个地表的下沉移动规律与一般开采引起的地表下沉位移规律相似.

（2）当松散层厚度固定时，随着基岩厚度的增加，最大位移与沉降值都在不断减小，单间小幅度在不断降低.最大位移值出现在开采工作面边缘处.在采空区影响范围边缘处与开采工作面边缘处之间的区域内，位移与沉降值随着岩层厚度的增加而出现了增大的规律，这与中心区域的规律截然相反.因为随着岩层厚度的增加，地表的位移与沉降值在不断减小，同时地表位移与沉降的影响范围也在不断扩大，这使得地表的变形变得越来越平缓，因此会出现这种现象.

（3）随着岩层厚度与松散层厚度之比的增加，地表的最大下沉速率和位移速率在不断地减小，当比值减小时，其最大下沉与位移速率呈增加趋势，但都是呈阶段性的线性变化.