R3上一类圆盘型Besicovitch集的Hausdorff维数估计

陈泽斌

（汕头大学理学院，广东 汕头515063）

0 引言

Kakeya在1917年提出了寻找单位直线段可以在其内部调转方向并且具有最小面积的平面集的问题.到了1928年，Besicovitch构造了一个令人惊奇的面积为零的平面集，它在所有方向上都包含一单位直线段，即R2上的Besicovitch集.取这种集与Rn-2的乘积集，就得到了Rn上的Besicovitch集.有一个已经很长时间的猜想是：Rn空间中的任意Besicovitch集的Hausdorff维数等于n.这就是著名的Kakeya猜想.关于Kakeya猜想，目前n=2的情形已完全解决并存在好几种证明方法，见文献[1-3].而对于高维（n≥3）的情形，1985年Christ-Duoandikoetxea-Rubio de Francia[4]首先证明了下界为到了1991年，Bourgain[2]利用一个称为“bush”的构造将其改进为这里εn是一个固定的数，只与n有关.而这项工作最突出的结果来自于Wolff，1995年Wolff[5]利用另一个称为“hairbrush”的更有效的构造再次将这个下界提高至其中对于3≤n≤8，这仍然是目前最好的结果.而对于n＞9，Katz-Tao[6]于2000年将其提高至由前面介绍可知在高维空间虽然已得到丰富的结果，但是我们可以看到，即使是n=3的情形，最好的结果也仅是2.5，距离最终结果3还差了很多.针对n=3，利用已有的构造和方法要想进一步提高这个下界是相当难的.那么一个比较自然的想法是，若仅对一类特殊的Besicovitch集进行维数估计，能否推出该类Besicovitch集的Hausdorff维数为3呢？本文以此作为出发点，将Kakeya问题二维情形的一种证明方法（参见文献[2]）推广到R3空间，定义了一类圆盘型Besicovitch集并对其进行维数估计.

1 定理的提出

1.1 相关定义

1.1.1 圆盘型Besicovitch集：记E集为R3上的圆盘型Besicovitch集，E集包含以ξ∈S1为法向量，点a为圆心的各个方向的单位圆盘，即

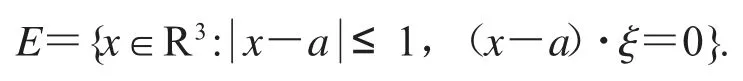
其中，R3是3维欧氏空间，S1是单位圆周.

1.1.2 δ-圆盘：令0＜δ≪1，对E中任一方向的圆盘，我们给其增加δ厚度，使其成为一个 δ-圆盘（见图1），记为（a），即

其中x⊥=x-（x·ξ）·ξ.

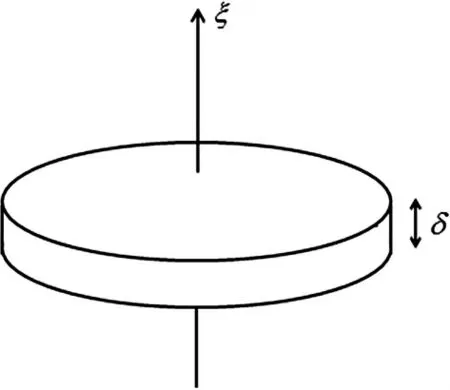
图1

1.2 主要结论

有了上述相关定义，下面我们给出本文的主要结论：

定理1 R3中的E集的Hausdorff维数为3.

2 预备知识

这一小节我们将简要介绍Hausdorff维数的一些相关概念：

令E⊂Rn，α＞0，对0＜δ≪1，定义：

其中κδ是E的可数覆盖，由半径ri＜δ的小球B（xi，ri）构成的集合，即

令δ→0，得到E的Hausdorff测度：

（1）若0≤α＜dimE，则Hα（E）=∞；

（2）若dimE＜α＜∞，则Hα（E）=0.

约定：本文我们约定对于f和g两个函数，f≾g表示存在常数C，独立于f和g，使得f≤Cg.

3 定理1的证明

下面我们将分为两个定理来证明.

成立，那么R3中的E集的Hausdorff维数为3.

证明 给定一个E集，注意到若E的Hausdorff维数不是3，那么便存在α＜n使得Hausdorff测度H（αE）为0.由于对我们只需证对于某些δ＞0，

这里

定义

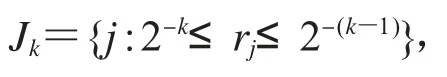
对于一个方向ξ∈S1，令dξ为其所对应的E中的单位圆盘.令

定义

所以

由（2）我们可以得到

因此

这里σ（Sk）指Sk的长度测度.

另一方面通过已知条件我们有

结合（3）可得

第二个不等号利用了k4≤Cε22kε.现在固定α＜n，选择ε＞0，使得α＜3-4ε，则

这里常数c与E的覆盖无关，所以（1）成立.证毕.

成立.

注意到我们有

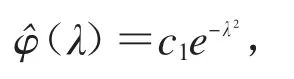
这里ξ∈S1.

令pξ∈SO（2），这里SO（2）为所有2阶行列式为1的正交变换的集合，转动使得因此我们有

所以

最后一个不等号运用了Hölder不等式.

对于（4）右边第二项，我们可以选择适当的坐标系使得ξ=e1，故有

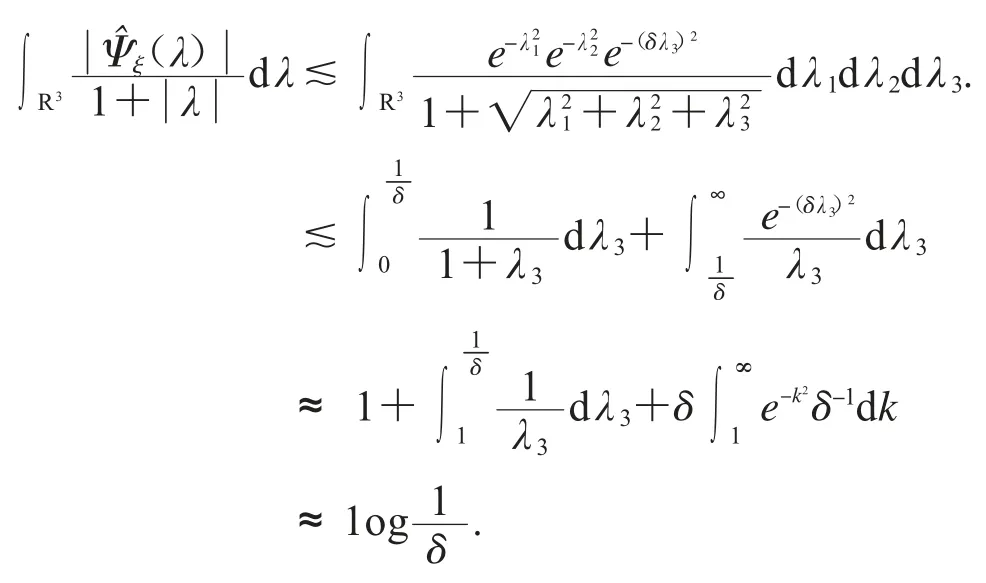
应用Fubini定理，我们可以得到

成立，由Plancherel定理可得

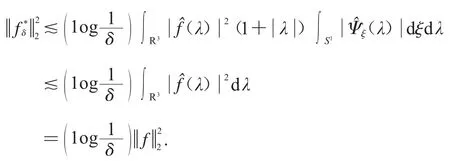
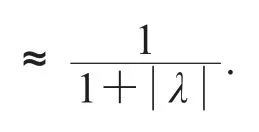
结合定理3.1和定理3.2，我们得到R3上的E集的Hausdorff维数为3.

本文定义了R3上一类圆盘型Besicovitch集并对其进行维数估计，证明了该圆盘型Besicovitc集的Hausdorff维数为3.因为Kakeya二维情形已有的证明方法不能推广到高维（n＞3）情形上，所以接下来我们将会致力于寻找高维情形新的证明方法.