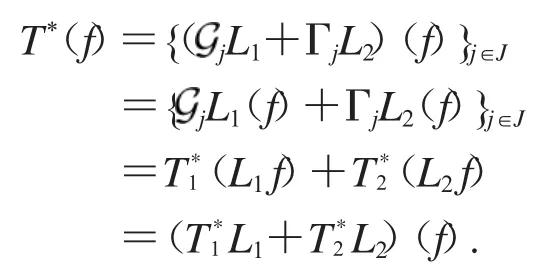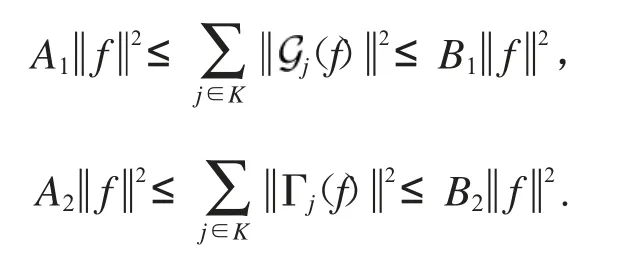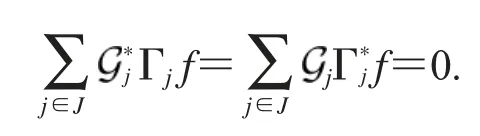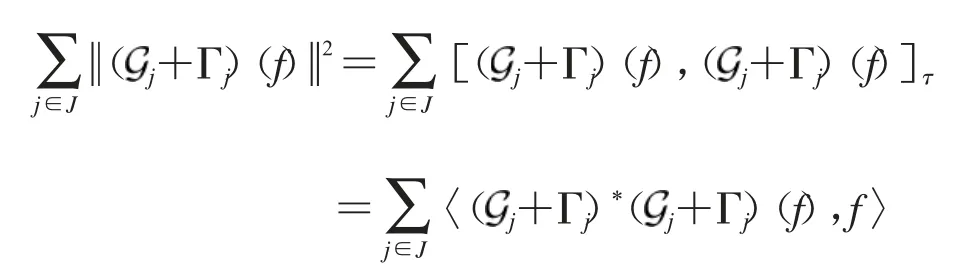关于Hilbert-Schmidt框架的一些性质

李文文，杨守志

（汕头大学理学院，广东 汕头515063）

0 引言

1952年，Duffin和Schaeffer[1]为了研究非调和Fourier级数问题，引入了框架的概念.但在后来几十年中，并未受到人们的重视，直到1986年，Daubechies，Grossman与Meyer的再次引入，使得框架重新进入大众的视野.在实际应用中，框架作为一个有用的工具，在很多领域都有应用，如信号处理、信号采样、神经网络、信号重构等.

随着对框架深入的研究，扩充原理引起很多研究者的关注.许多作者围绕这一方面进行研究：1997年，Ron与Shen[2-3]对任意的一个小波序列可通过添加一个元素，把小波Bessel序列扩充成为紧小波框架；而后，Casazza与Leonhard[4]提出了在有限维空间中，任意的Bessel序列都可以扩充为紧框架；Li与Sun[5]将结果延伸到了无限维的情况；后来，Christensen，H.O.Kim和R.Y.Kim[6]把Bessel序列扩充到更一般的对偶框架对.

而在框架概念的基础上，好几种框架的推广被提出，如g-框架、融合框架、斜框架、HS-框架等.在文献[7]中，作者提出了g-框架的定义，把g-框架的概念从有界线性泛函推广到了算子的形式，并利用g-框架对几种框架进行了统一，说明了有界的准投影器[8]、子空间的框架[9]、伪框架[10]、斜框架[11]、外框架[12]和时间频率定位算子[13]都是g-框架的特殊情况，也即这几种框架的某些性质仍然适用于g-框架.

在文献[14]中，作者给出了在Hilbert空间中，两个框架相加的情况.后来在文献[15-16]中，作者把框架的相加的情况推广到了g-框架.文献[17]给出了关于g-框架扰动的一些结果.Ghadir Sadeghi与Aliakbar Arefijamaal[18]通过von Neumann-Schatten p-框架，给出了当p=2时Hilbert-Schmidt框架的概念，简称为HS-框架.并且给出了g-框架与HS-框架之间的关系：设{Λj}j∈J为H中关{Kj}j∈J的g-框架，则{Λj}j∈J是H中关于的HS-框架，所以g-框架可以看作HS-框架.因此g-框架的一些性质适应于HS-框架.

下面有一些文中的符号的表示，H，K为Hilbert空间，{Kj}j∈J为K中的一列闭子空间，{Λj}j∈J为算子序列，Z为整数集，其中J、I为Z的子集，表示从H到K上的有界线性算子的全体.若H=K，则记为既是Banach空间又为Hilbert空间.

1 基础知识

定义1[1]设序列{fj}j∈J是可分的Hibert空间H的序列，且存在常数0＜A≤B＜∞，使得

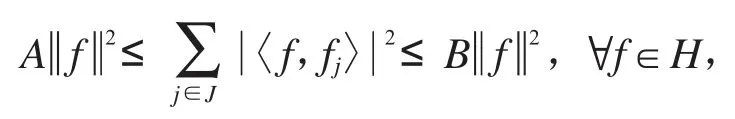
称{fj}j∈J为H上的框架.其中A、B分别为框架的下界和上界.若仅有右边的不等式成立，则称{fj}j∈J是一个界为B的Bessel序列.当A=B时，则称{fj}j∈J为紧框架.若A=B=1，则称{fj}j∈J为Parseval框架.

设框架{fj}j∈J是Bessel序列，T为{fj}j∈J的合成算子，对有

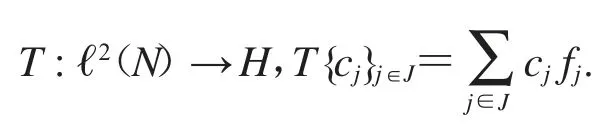
定义T的伴随算子T*为分析算子，对有

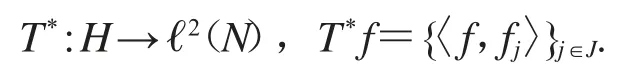
明显有，{fj}j∈J是框架当且仅当分析算子T*是可逆算子.

设{fj}j∈J和{gj}j∈J都为H中的Bessel序列，若

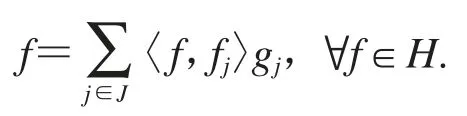
则称{gj}j∈J为{fj}j∈J的对偶框架.当{fj}j∈J={gj}j∈J时，有

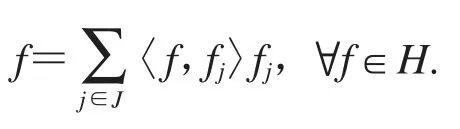
知{fj}j∈J为紧框架，框架界是A=B=1.

下面介绍g-框架的定义.

定义2[7]称算子列为H中关于{Kj}j∈J的推广框架，简称为g-框架，若存在0＜A≤B＜∞，使得对有

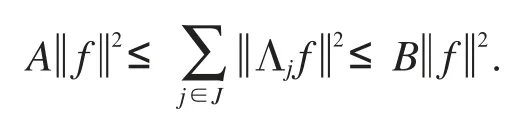
其中A和B分别称为g-框架的上界和下界.若仅有右边不等式成立，则称{Λj}j∈J是一个g-Bessel序列.若A=B，则称为紧g-框架.若A=B=1，则称{Λj}j∈J为Parseval g-框架.

关于g-框架更详细的内容可以参考文献[7].根据文献[18]，下面给出HS-框架的定义.

定义3[18]称是从H到的Hilbert-Schmidt框架或简称在H中关于K的HS-框架，如果0＜A≤B＜∞，对有

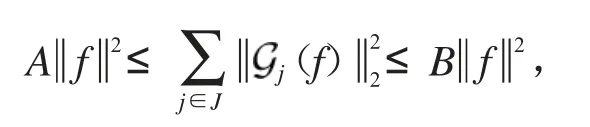
其中A和B分别称为HS-框架的上界和下界.若仅有不等式右边部分成立，则称为HS-Bessel序列并且框架界为B.若A=B，则称为H到K中的紧HS-框架.若A=B=1，则称其为Parseval HS-框架.

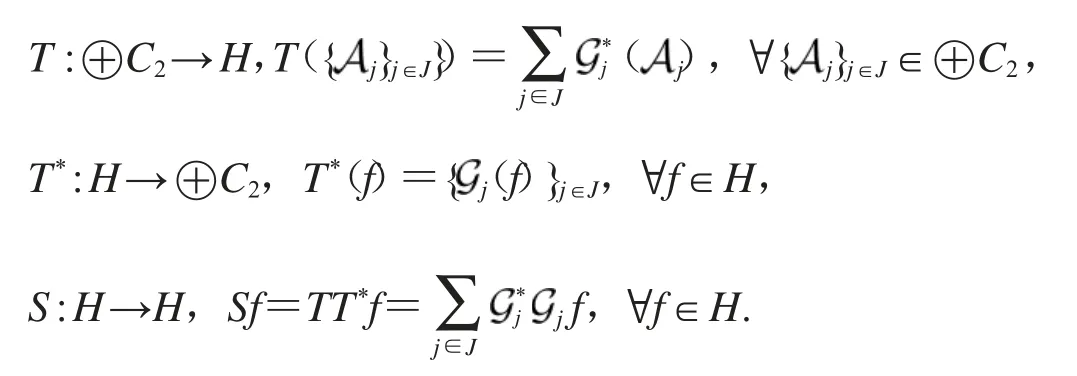
其中框架算子S是有界可逆正定自伴.

引理1[19]序列为HS-Bessel序列且界为当且仅当合成算子T:⊕C2→H的定义为

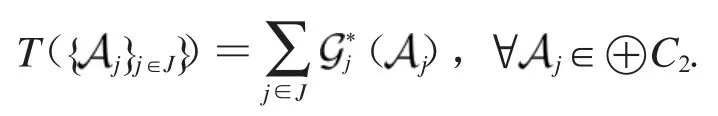
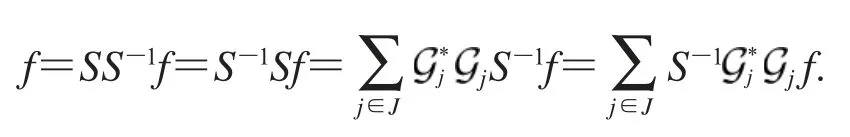
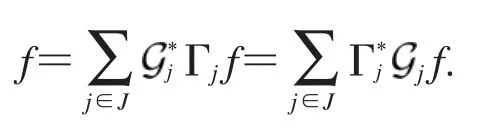
2 HS-Bessel序列的扩充

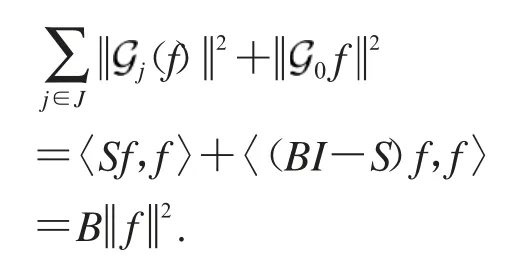
证明 令S为HS-Bessel序列的框架算子，则可知BI-S仍为自伴正定算子，设序列{ei}i∈I为H中的标准正交基，使用{ei}i∈I来展开有

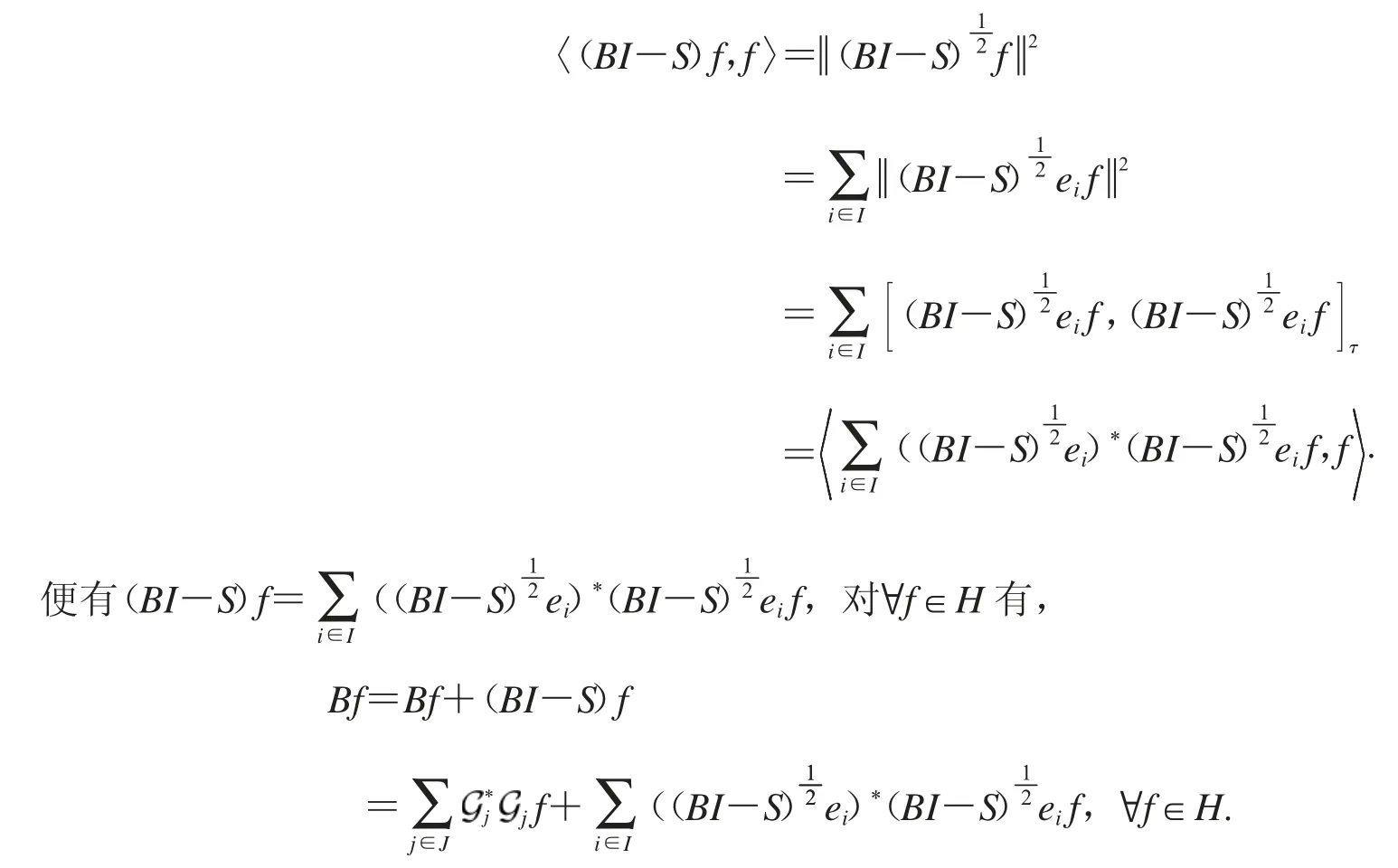
证明 设S1、S2分别为的框架算子，令{ai}i∈I与{bi}i∈I为任意的对偶HS-框架对，有

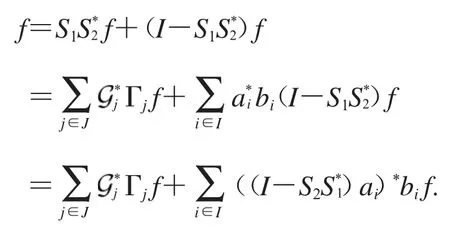
3 HS-框架相加

所以，有

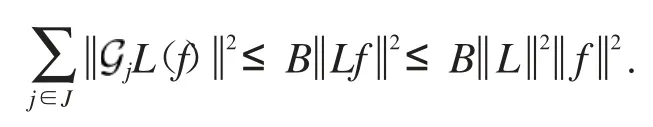
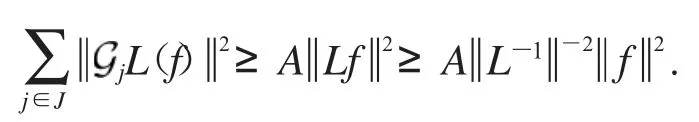
证明 根据定理4，令L=S-1即可.

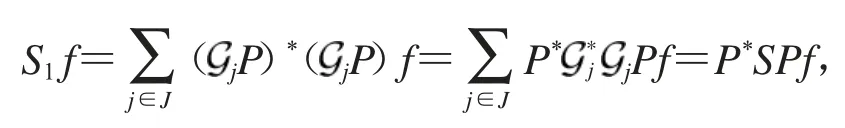
证明 设I+L在H中可逆，由定理4有

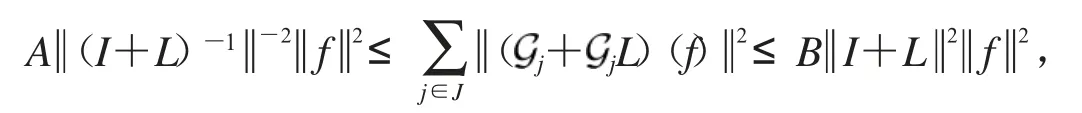
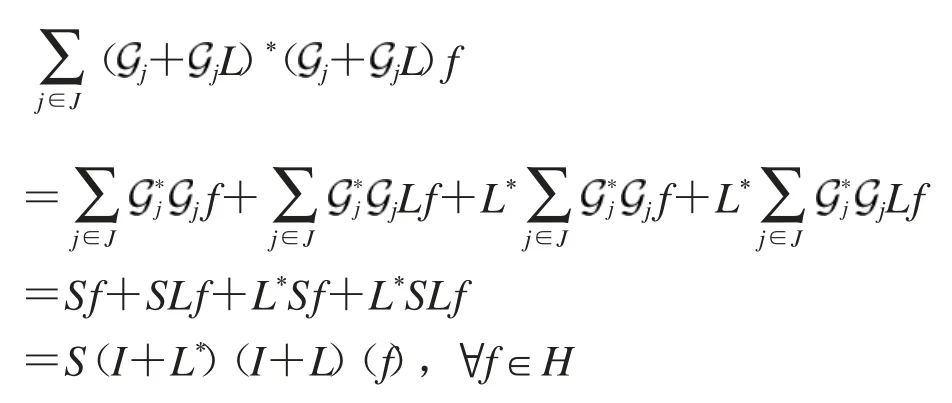
所以，有I+L在H中可逆.