核电部件屈曲设计方法的对比分析与案例研究
2019-08-15宫建国黑宝平2高付海2轩福贞
刘 芳,宫建国,黑宝平2,高付海2,轩福贞
(1.华东理工大学 机械与动力工程学院,上海 200237;2.中国原子能科学研究院,北京 102413)
0 引言
屈曲是快堆关键部件的重要失效模式,涉及地震载荷下的反应堆主容器、轴压载荷下的泵和换热器支撑筒等部件。按照服役温度[1-2]的不同,其失效模式又可分为瞬时屈曲(时间无关屈曲)失效和蠕变屈曲(时间相关屈曲)失效。与瞬时屈曲相比,蠕变屈曲一般发生在服役一段时间后、且温度较高的环境,其临界载荷低于瞬时屈曲载荷,原因在于蠕变变形加剧了缺陷对临界载荷的不利影响[3]。为保证反应堆安全可靠地运行,核电部件的屈曲设计问题至关重要。
目前,国际上已有相关设计规范[4-7]可用于核电部件的瞬时屈曲和蠕变屈曲设计中。本文分别介绍针对瞬时屈曲和蠕变屈曲的现有设计方法。
对于瞬时屈曲设计,ASME NB[4]中基于屈曲弹性解,给出圆柱壳、球壳等结构的设计方法;ASME NH[5]中提供了瞬时屈曲设计系数,该系数适用于所有结构和载荷。RCC-MRx[6]中基于屈曲弹性解,也给出了圆柱壳和球壳等结构的屈曲设计方法,该方法与ASME NB相同。此外,RCC-MRx给出了瞬时屈曲设计系数,并且在附录A7中提出用于屈曲强度评价的弹性和非弹性分析方法,其中弹性分析需要保证结构的应力水平不能超过标准中的许用值;对于非弹性分析,需对结构进行详细的非弹性屈曲分析,判断结构在施加载荷下是否满足标准中的屈曲准则。上述两种方法都是针对恒载屈曲分析,附录A7中还提供了两种用于循环载荷的屈曲设计方法:方法一是将等效应力限制在许用应力范围内;方法二是将等效应力限制在失稳应力范围内。
对于蠕变屈曲设计,ASME NH中提供蠕变屈曲设计系数,需要保证设计寿命内,当施加的载荷等于设计载荷乘以设计系数时,结构不会发生屈曲失效。此外,对于轴压圆柱壳蠕变屈曲设计,ASME Code Case 2676(CC2676)[7]中提出一种基于弹性屈曲解和等时应力应变曲线的设计方法。RCC-MRx中也提供了蠕变屈曲设计系数,并且在附录A7中提出一种蠕变屈曲的简化设计方法,该方法基于含缺陷的外压圆环模型以及弹性屈曲理论,适用于薄壳结构。
目前,关于不同规范中所涉及屈曲设计方法的案例比较研究,尚未有相关文献报道。为进一步系统评价不同屈曲设计方法的适用性,本文在调研ASME和RCC-MRx设计方法的基础上,结合轴压圆柱壳典型案例,开展现有屈曲分析方法的比较研究。
1 瞬时屈曲设计方法
1.1 ASME规范
1.1.1 ASME NB
不超过蠕变温度时,轴压圆柱壳、外压圆柱壳、外压球壳等部件可按照ASME NB中的方法进行屈曲设计,该设计方法基于薄膜理论和弹性屈曲理论。通过将弹性屈曲解分解为应变和应力两项,加入安全系数,分别得到应变A和许用应力B,许用应力根据弹性计算公式或外压设计曲线得到,再通过薄膜理论得到结构的许用载荷。ASME Ⅱ[8]中给出了不同材料的外压设计曲线,这些设计曲线是通过拉伸曲线转换得到的,转换方法见文献[8]。不同工况下的屈曲载荷(应力)等于许用载荷(应力)乘以表1中的系数。其设计方法如下。

表1 不同工况下用于屈曲设计的载荷
(1)轴压圆柱壳。
首先采用式(1)计算应变A;再根据材料和工况选择外压设计曲线;最后根据A从外压设计曲线中确定许用应力B。当A在设计曲线的左侧或者弹性段时,也可按照式(2)确定B;当A落在曲线右侧时,作设计曲线的水平延伸线与纵轴相交,交点值即为B。
(1)
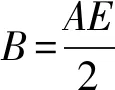
(2)
(2)外压圆柱壳。
当Do/t≥10,根据L/Do和Do/t,查ASME Ⅱ中的外压圆柱壳参数曲线,确定应变A;再根据A和外压设计曲线确定许用应力B,确定方法与轴压圆柱壳相同;最后根据式(3)或(4)确定许用载荷。
(3)
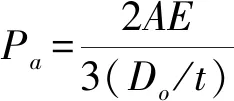
(4)
当Do/t<10,根据外压圆柱壳参数曲线确定A;当Do/t<4时,也可根据式(5)确定A;最后采用式(6),(7)计算许用载荷Pa1和Pa2,选择二者中的较小值作为许用载荷。
(5)
(6)
(7)
(3)外压球壳。
应变A的确定方法与轴压圆柱壳相同,因此可根据式(1)确定A,再采用式(8)或(9)计算许用载荷。
(8)
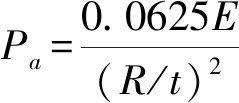
(9)
1.1.2 ASME NH
ASME NH中将屈曲分为两类,一类是载荷控制屈曲,此类屈曲在结构进入后屈曲阶段,载荷仍然保持不变;另一类是应变控制屈曲,结构屈曲后载荷会减小,具有自限性,危险程度小于载荷控制屈曲。对于上述两种类型的屈曲,ASME NH中给出不同工况下的设计系数,如表2所示。当载荷(应变)系数(见式(10))大于表2中给出的系数时,满足设计要求,但目前标准中还未提供屈曲分析方法。
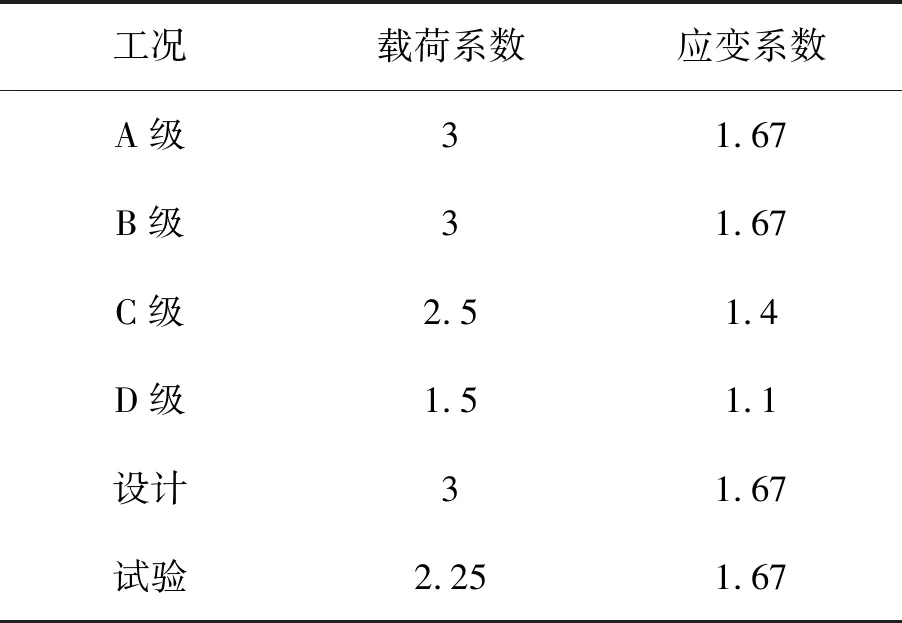
表2 不同工况下瞬时屈曲设计系数(ASME NH)
1.2 RCC-MRx标准
1.2.1 RB3270
RCC-MRx中对屈曲的分类与ASME相同,
分为载荷控制屈曲和应变控制屈曲,不同工况下的载荷系数如表3所示。对于应变控制屈曲,不规定设计系数,但在弹塑性失稳、疲劳和过度变形中应考虑屈曲的影响。

表3 不同工况下瞬时屈曲载荷系数(RCC-MRx)
1.2.2 附录A7
附录 A7中给出用于屈曲强度评价的弹性和非弹性分析方法,分析流程分别如下。
(1)弹性分析方法。
弹性分析流程如图1所示。通过弹性分析计算结构薄膜应力和薄膜加弯曲应力,屈曲判定准则如表4所示,其中,应力强度(σm)l,(σm+b)l,(σL+b)l应根据附录A7中给出的应力强度曲线确定。
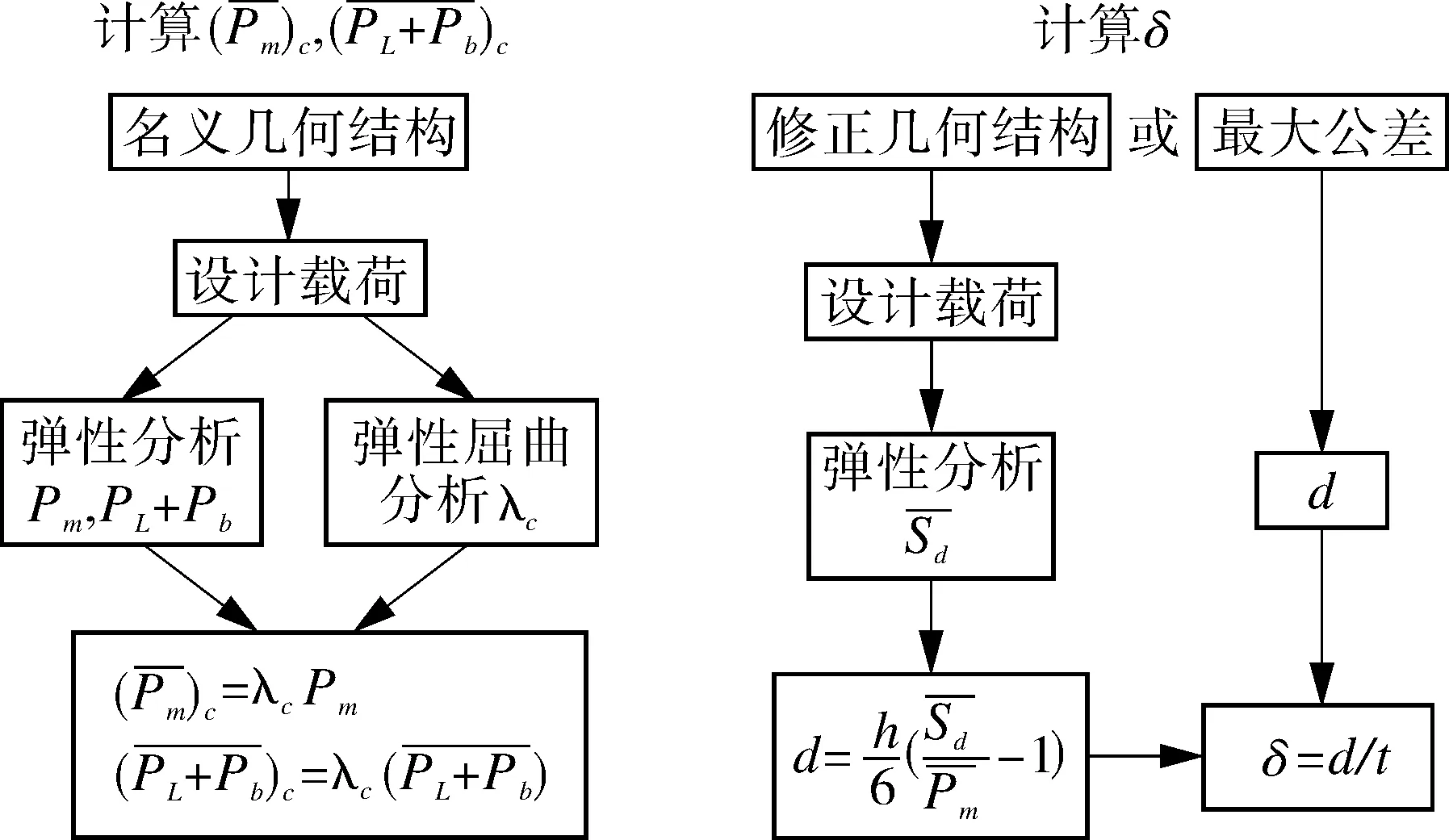
图1 弹性分析流程

表4 弹性分析判定准则
(2)非弹性分析方法。
非弹性分析流程见图2,其中,最大缺陷为设计说明书中规定的最大公差,模态为第1阶屈曲模态,分析过程中考虑大变形,使用最小拉伸曲线,施加载荷L等于设计载荷乘以表3中的载荷系数。若分析结果满足判定准则,则结构不会发生屈曲失效。
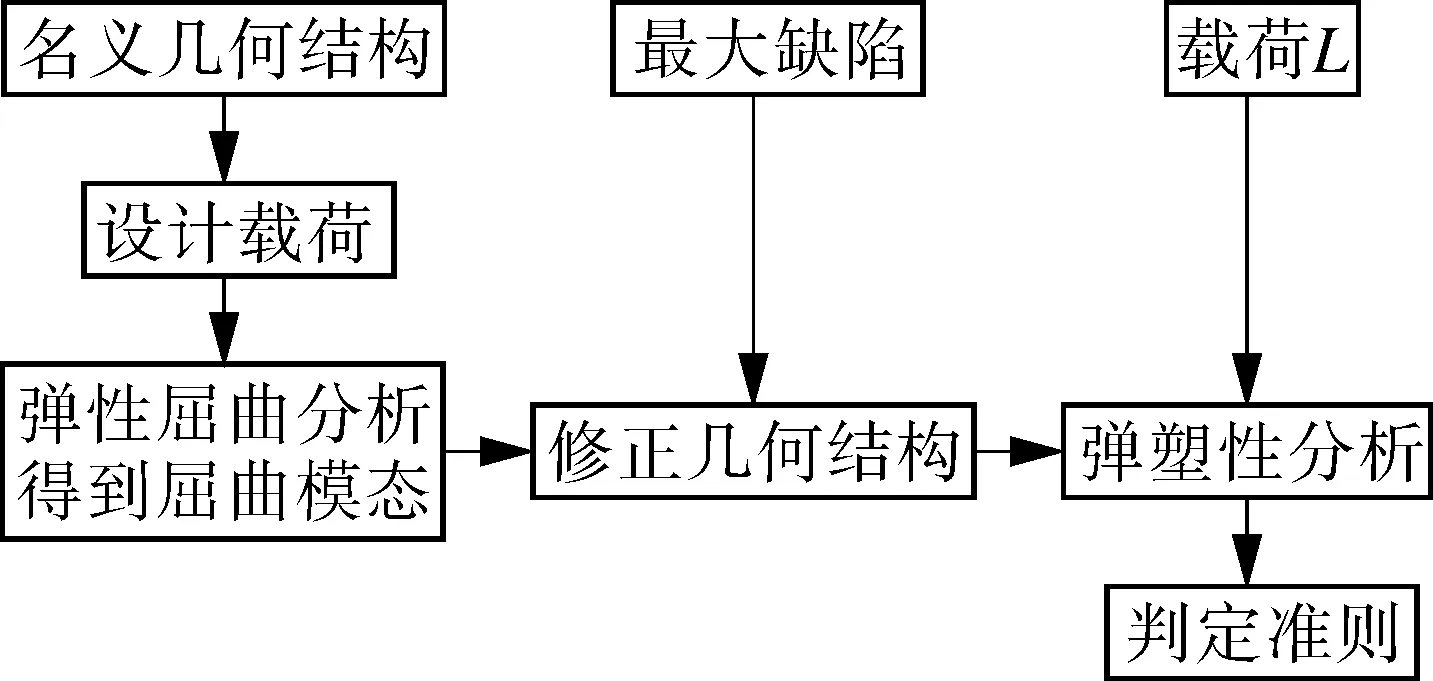
图2 非弹性分析流程
图2中的判定准则如下:
(1)对于载荷λL(λ≤1),结构处于稳态;
(2)结构在载荷L下不会发生分叉屈曲;
(3)在载荷L下,结构的变形不会很大。
由上述分析流程可以看出,弹性屈曲分析需要进行应力分类,分类结果会因设计者不同而有所差异;非弹性分析可以避免应力分类问题。
上述弹性和非弹性分析方法都是针对恒载屈曲问题,附录A7中还提供了循环载荷下的屈曲分析方法,包括方法1和方法2,其分析流程分别如下。
(1)方法1:将等效应力限制在许用应力内。
其分析流程如图3所示。
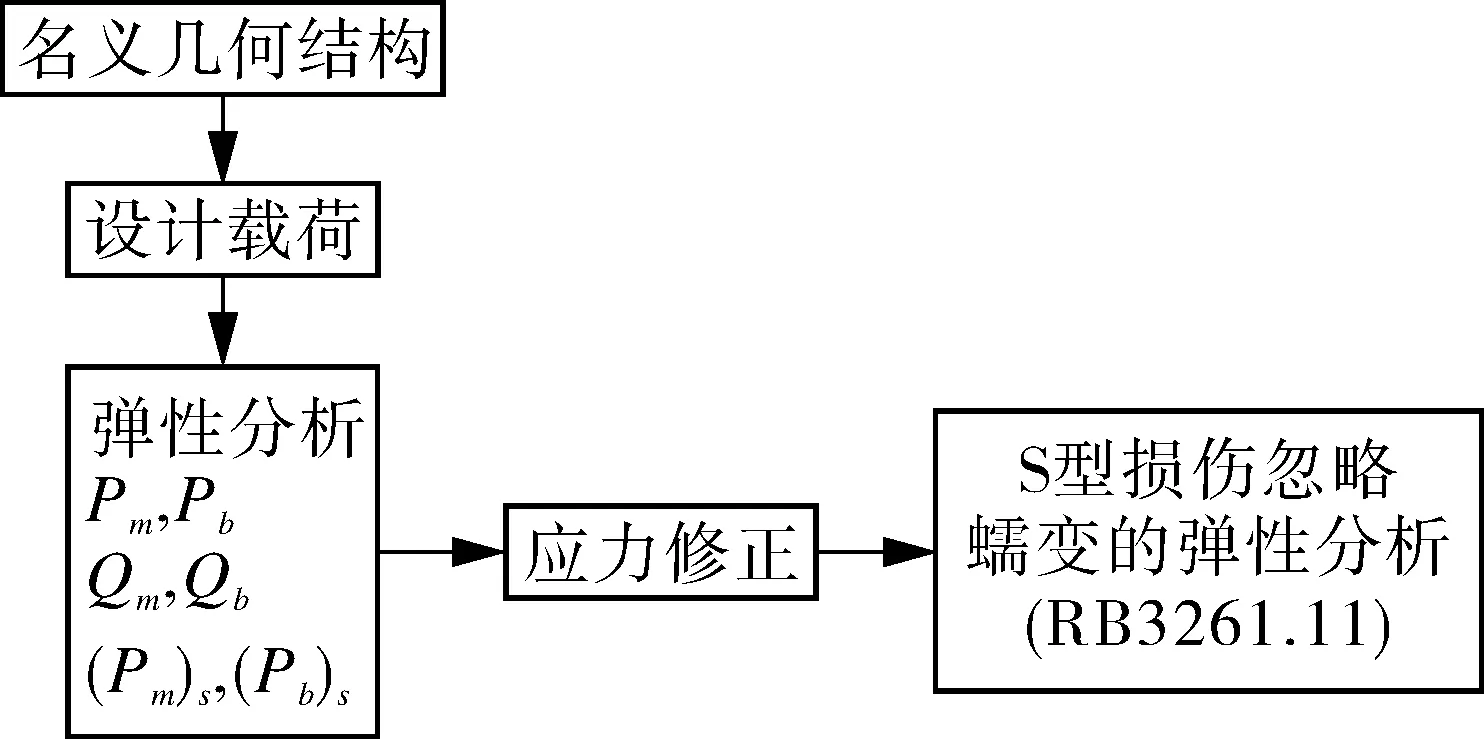
图3 循环载荷下屈曲分析流程(方法1)
采用S型损伤忽略蠕变的弹性分析方法,分别按照累计变形准则、疲劳准则进行评定。此外,结构还需满足弹性屈曲分析或非弹性屈曲分析中的设计准则。
(2)方法2:将等效应力限制在失稳应力内。
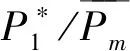

图4 循环载荷下屈曲分析流程(方法2)
1.2.3 附录A12
对于外压旋转薄壁容器和轴压载荷下的圆柱壳,附录A12给出另一种设计方法,该方法与ASME NB中的方法相同,本节不再详细说明。对于不同工况下的许用载荷,计算得到的载荷应乘以表5中的系数。

表5 不同工况下用于屈曲设计的载荷
1.2.4 附录A15
对于内压作用的椭球、碟形封头,在过渡区会产生环向压应力,因此,局部屈曲是椭球和碟形封头的一种重要失效模式。附录A15中给出了封头最小厚度的计算方法,主要考虑3种失效模式:顶部爆破失效、过渡区屈服失效、过渡区局部屈曲失效。防止顶部爆破失效的设计基于等效球壳的中径公式(见式(11));防止过渡区屈服的设计基于文献[9]中的方法,考虑大变形和理想弹塑性材料模型,推导得到内压-位移曲线,根据两倍弹性模量确定封头失效压力,再结合工程经验[10]得到屈服设计公式(见式(12));防止过渡区局部屈曲失效的设计基于Galletly公式[11],考虑大变形和理想弹塑性材料模型,通过对有限元计算结果进行数据拟合[12],得到屈曲预测公式[13],再结合试验结果得到屈曲设计公式[14](见式(13))。最小壁厚取这三者中的最大值(见式(14))。当ey>0.005Di,计算时不需要考虑局部屈曲失效。
(11)
(12)
e=Max(es,ey,eb)
(14)
2 蠕变屈曲设计方法
2.1 ASME规范
2.1.1 ASME NH
载荷控制屈曲的设计系数如表6所示。对于应变控制屈曲,蠕变明显时结构对屈曲的抗力下降,但随着应变增加,结构中的载荷也会下降,所以对于应变控制屈曲,其应变系数取1。目前标准中还未提供蠕变屈曲分析方法。

表6 不同工况下蠕变屈曲载荷系数(ASME NH)
2.1.2 CC2676
CC2676中给出轴压圆柱壳蠕变屈曲设计的另一方法,该方法由Jawad等[15]提出,与ASME NB中的设计方法相似,都是根据弹性屈曲理论得到,但是外压设计曲线是通过等时应力应变曲线转换得到的,转换方法见文献[15]。根据式(15)计算应变A,采用设计曲线或式(2)确定许用应力B,其方法与ASME NB中的方法相同。蠕变屈曲设计中需采用一个减小的模量来替代弹性屈曲解中的弹性模量,设计中一般取切线模量作为减小的模量,随着蠕变时间增长,从等时应力应变曲线中得到的切线模量与真实减小的模量相比越来越保守,因此,蠕变屈曲设计中引入参数K1(见式(16))来减小设计的保守性。
(15)
(16)
2.2 RCC-MRx标准
2.2.1 RB3270
RB3270中给出蠕变屈曲载荷设计系数,如表7所示。对于应变控制的屈曲,不规定设计系数,但在弹塑性失稳、疲劳和过度变形中应该考虑屈曲的影响。

表7 不同工况下蠕变屈曲载荷系数(RCC-MRx)
2.2.2 附录A7
附录A7中提出一种蠕变屈曲简化设计方法,可用于薄壳结构的蠕变屈曲设计。该方法由Combescure[16-17]提出,根据外压圆环的薄膜理论和屈曲弹性解,假设圆环含正弦型几何缺陷,结合材料蠕变本构方程,通过理论推导可得蠕变屈曲控制方程,将方程绘制成蠕变屈曲设计曲线,如图5所示。其主要流程如下。
(1)根据操作温度θ以及蠕变时间T判断是否需要考虑蠕变影响,如果不需要考虑蠕变,可按瞬时屈曲进行设计;
(2)计算操作温度下弹性屈曲载荷Pe和屈服载荷Py,不考虑几何缺陷的影响;
(3)根据Pe/Py选择合适的设计曲线;
(4)计算比值x=P/Pe(其中,P等于设计载荷乘以设计系数);
(5)确定缺陷系数δ=d/t;
(6)若(x,δ)落在时间设计曲线下面,说明结构寿命期内不会发生蠕变屈曲。
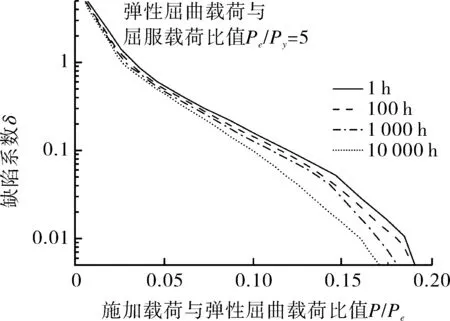
图5 316L-N蠕变屈曲设计曲线(550 ℃)
3 ASME规范和RCC-MRx标准屈曲设计方法对比分析
ASME规范和RCC-MRx标准中屈曲设计方法比较如表8所示。ASME NB中基于弹性屈曲理论提出瞬时屈曲的设计方法;ASME NH中提出适用于所有结构瞬时屈曲和蠕变屈曲设计的设计系数;对于轴压圆柱壳,CC2676中提出一种基于弹性屈曲解和等时应力应变曲线的蠕变屈曲设计方法。目前,ASME中还未提出适用于一般结构的屈曲分析方法。RCC-MRx在RB3270中提出屈曲设计系数,并且在附录A7中给出弹性和非弹性分析方法;对于圆柱壳和球壳瞬时屈曲设计,附录A12中的设计方法与ASME NB中的方法相同;对于内压封头局部屈曲设计,附录A15中的设计方法基于理想弹塑性材料模型和大变形假设,根据有限元分析结果和试验数据得到屈曲设计公式;针对薄壳蠕变屈曲设计,附录A7中基于含缺陷的外压圆环模型以及材料蠕变本构方程,结合弹性屈曲理论进行推导,得到设计曲线。
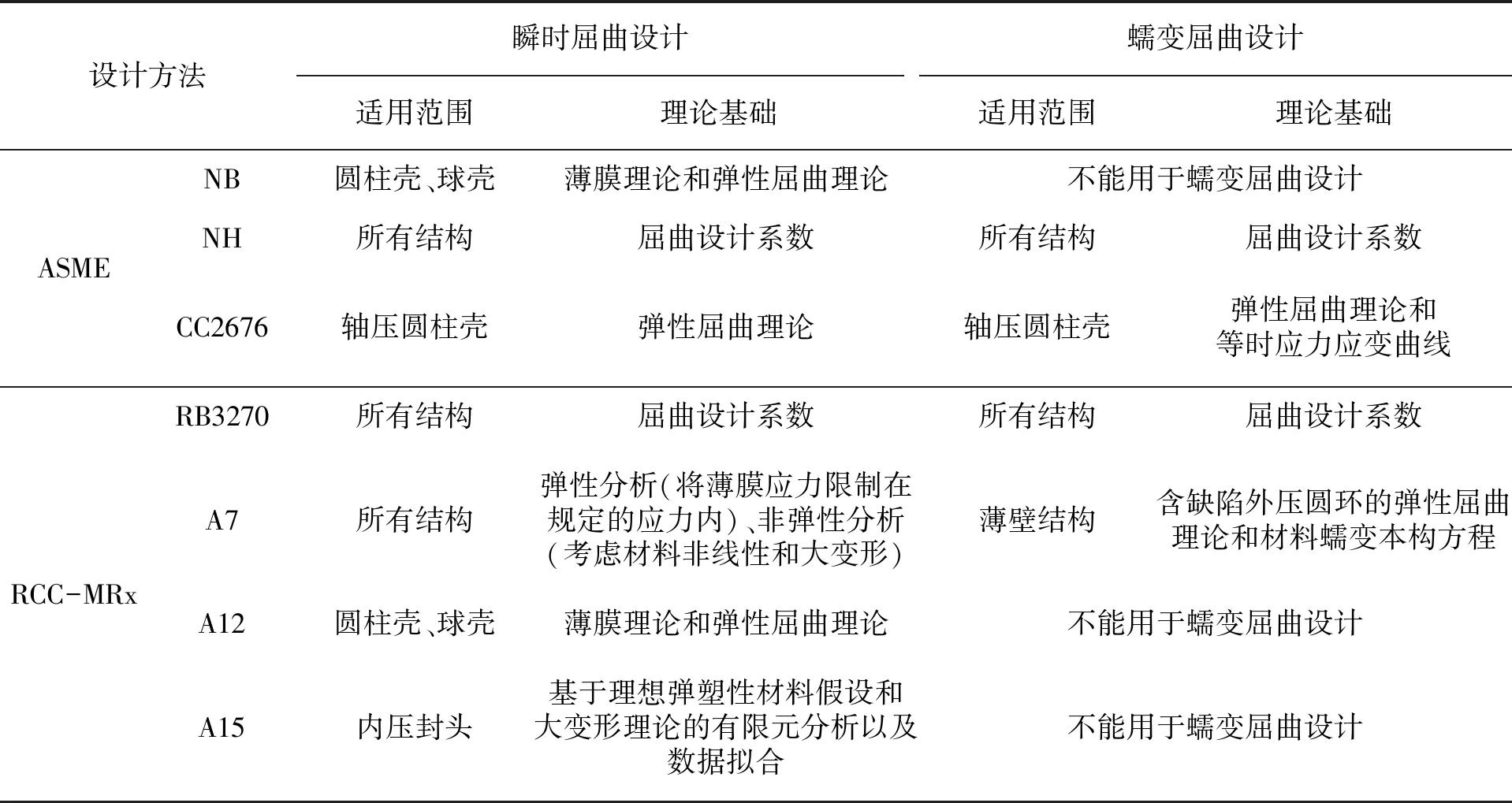
表8 ASME规范和RCC-MRx标准屈曲设计方法比较
4 基于ASME规范和RCC-MRx标准屈曲设计方法的算例研究
4.1 有限元分析模型
为了详细介绍ASME规范和RCC-MRx标准在屈曲设计上的应用,本文以轴压圆柱壳为例进行说明。圆柱壳长度L=3 000 mm,直径Do=2 000 mm,壁厚t=10 mm。在ABAQUS中建立圆柱壳模型,采用S4R单元进行网格划分,共生成14 442个单元,网格模型如图6所示。在圆柱壳上端施加均匀轴压载荷,壳体下端节点全部固定,上端限制除轴向平动以外的所有自由度,如图6所示。由于ASME和RCC-MRx中缺少某些材料数据,所以进行瞬时屈曲和蠕变屈曲分析时分别采用不同的材料,其材料性能如表9所示。
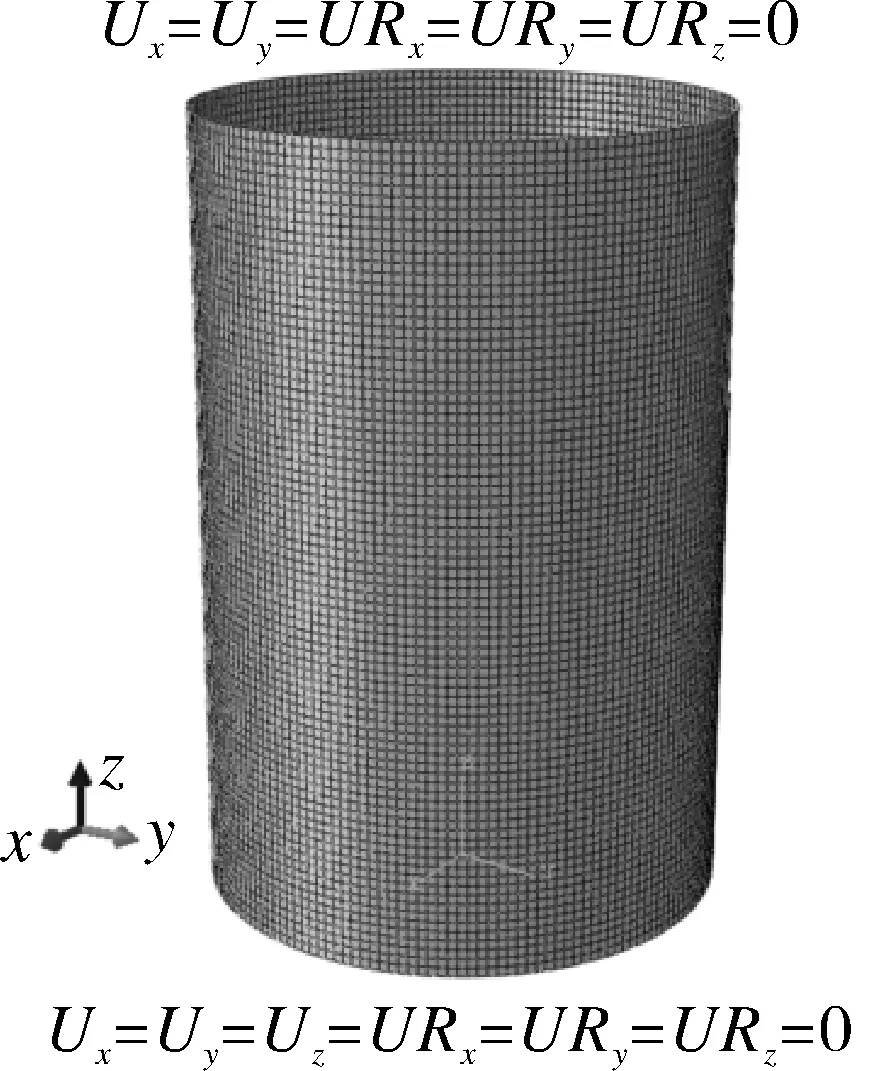
图6 圆柱壳网格模型

表9 316L,2.25Cr-1Mo,316L-N材料参数
计算圆柱壳屈曲载荷时,首先进行特征值分析,将特征值分析得到的第1阶屈曲模态作为初始几何缺陷导入非线性屈曲分析中,缺陷幅值等于壁厚,即缺陷系数等于1。最后根据非线性屈曲分析得到的危险点的载荷-位移曲线来确定临界轴压载荷。在非线性屈曲分析中,瞬时屈曲分析采用最小拉伸应力应变曲线,蠕变屈曲分析采用对应蠕变时间下的最小等时应力应变曲线,由于ASME NH中提供的是平均应力应变曲线,所以应按照文献[15]中的方法,得到最小等时应力应变曲线。对于316L-N,ASME NH中没有提供该材料的等时应力应变曲线,由于316SS与316L-N材料属性较为接近,因此,本文采用316SS的等时应力应变曲线近似代替316L-N。
4.2 有限元分析结果
特征值屈曲分析见图7(a),屈曲模态为向内或向外鼓起的坑状变形。将第1阶模态作为初始几何缺陷导入非线性屈曲分析中,非线性分析屈曲模态如图7(b)所示,变形呈凹坑状,绘出危险点的载荷-位移曲线如图7(c)所示。可以看出,载荷先是随着位移的增加而增大,达到临界点A后,载荷随位移的增大而减小,结构进入后屈曲,故取临界点处的载荷为临界屈曲载荷。本节中有限元分析结果以瞬时屈曲为例进行说明,对于蠕变屈曲,变形模态基本相同,不再详细说明。
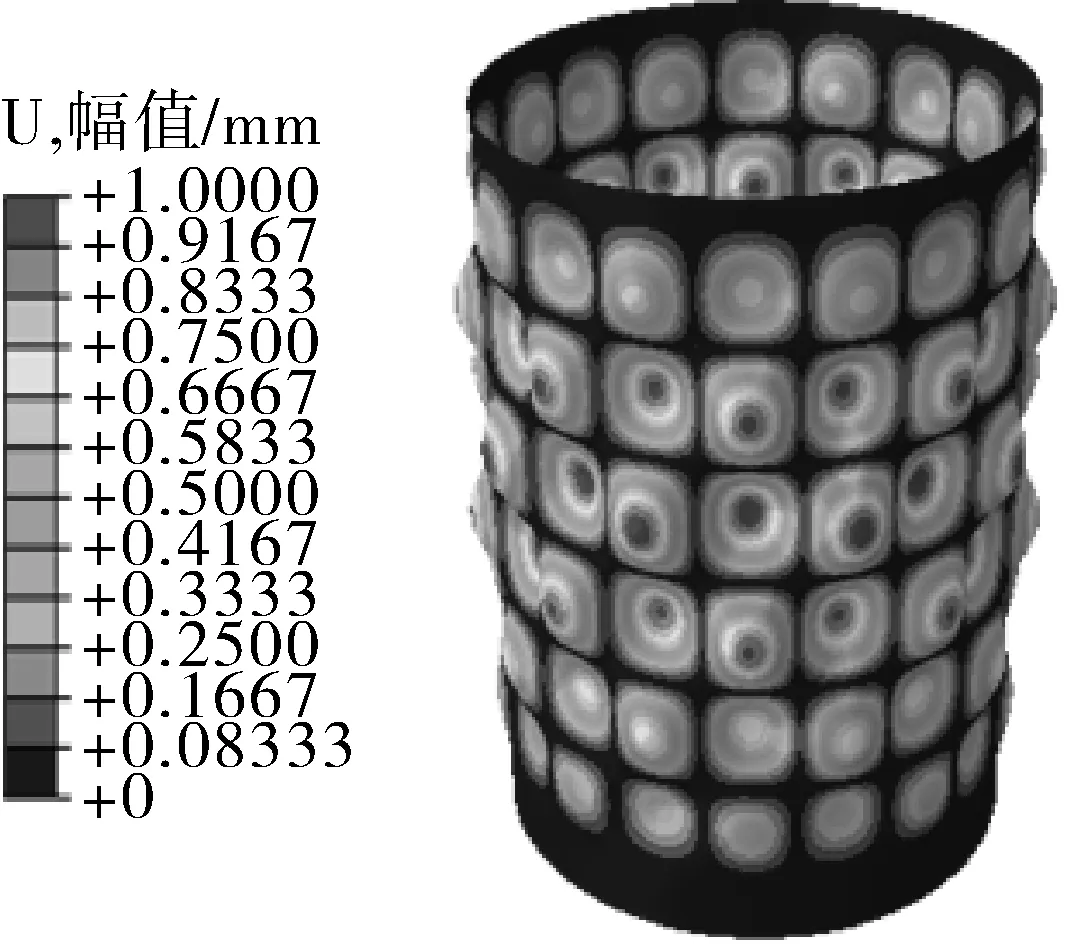
(a)特征值分析第1阶模态(变形系数=100)

(b)非线性分析屈曲模态
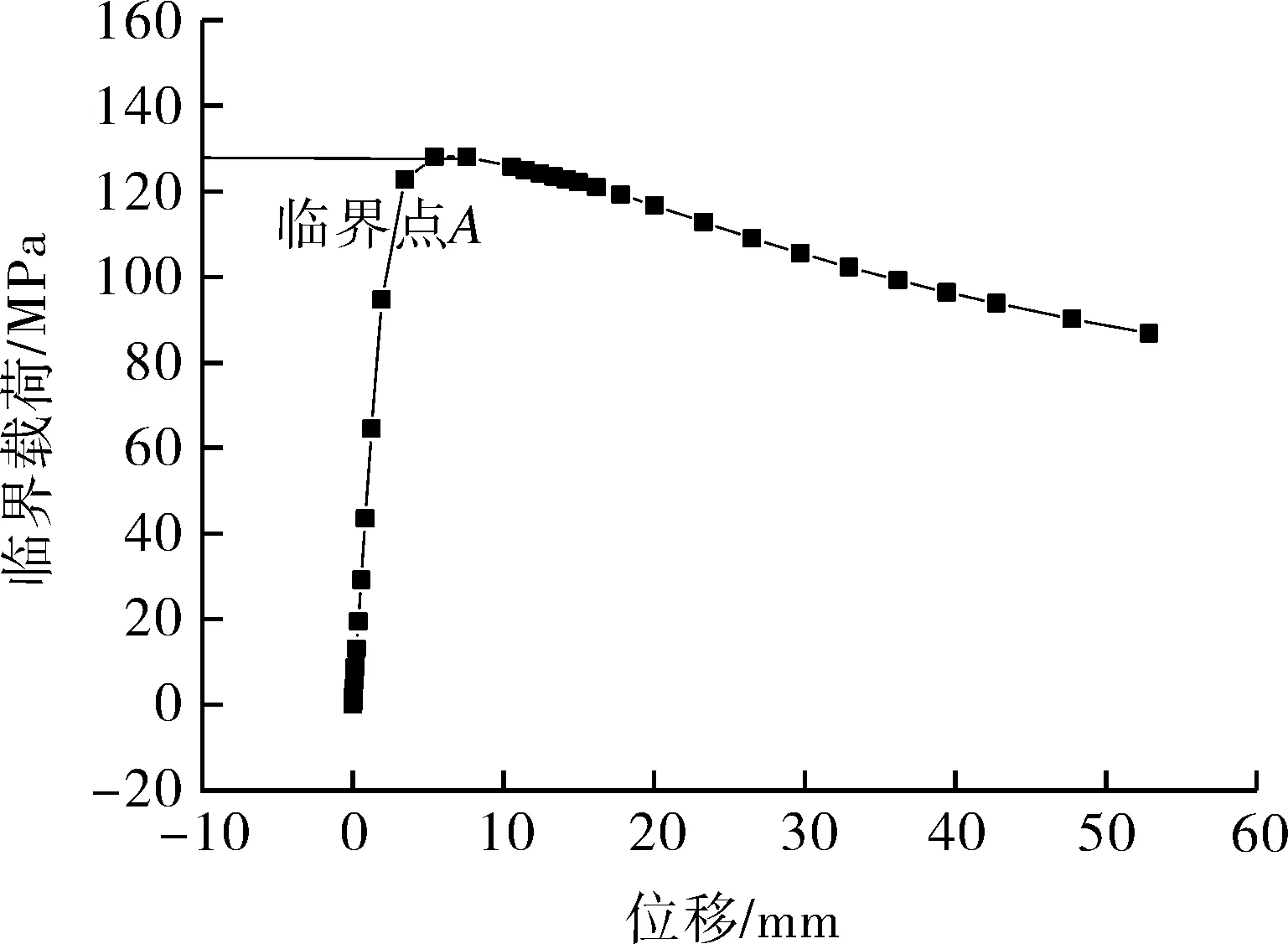
(c)临界载荷-位移曲线
4.3 瞬时屈曲设计比较
根据有限元分析求得的临界载荷,分别除以安全系数3.0(ASME NH)和2.5(RCC-MRx),得到许用应力。根据第1.1.1节中所述,按照ASME NB中的方法求得许用轴压应力。采用不同方法得到的许用应力见表10。可以看出,采用ASME NH计算得到的结果最保守,RCC-MRx方法次之,ASME NB的方法最危险。
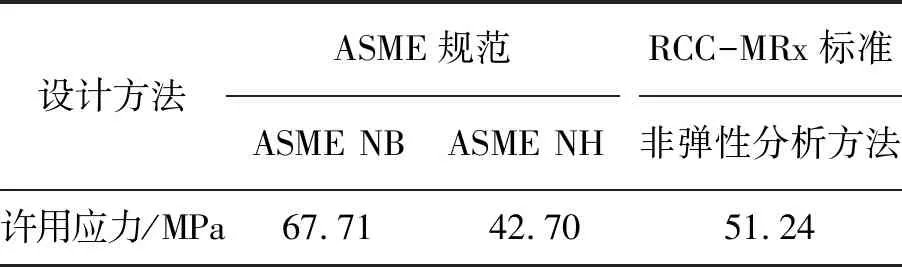
表10 瞬时屈曲许用应力比较
4.4 蠕变屈曲设计比较
分别采用2.25Cr-1Mo和316L-N的等时应力应变曲线作为材料的非线性数据进行有限元分析,蠕变时间为10 000 h。得到的临界载荷除以安全系数1.5(ASME NH和RB3270)后,可得到圆柱壳蠕变屈曲许用应力。再分别按照第2.1.2节中CC2676的方法和第2.2.2节中附录A7的方法计算许用应力,采用不同方法得到的许用应力如表11所示。可以看出,与有限元分析结果相比,CC2676和简化分析方法都是安全的,但简化分析方法的保守性更大。

表11 蠕变屈曲许用应力比较
5 结论
本文针对快堆屈曲失效模式,介绍了现有的屈曲设计方法(包括ASME规范和RCC-MRx标准),并以轴压载荷下的圆柱壳为例,开展了基于上述方法的案例研究,得到结论如下。
(1)对于瞬时屈曲设计,ASME NB和RCC-MRx中提出基于弹性屈曲理论的设计方法,两个标准中的方法相同,且只针对圆柱壳和球壳。对于一般结构的屈曲设计,ASME NH和RCC-MRx中提出了用于屈曲设计的载荷(应变)系数,但目前ASME NH中还未提供明确的分析方法,RCC-MRx附录A7中提供了屈曲强度评价的弹性分析方法和非弹性分析方法。
(2)对于蠕变屈曲设计,ASME NH和RCC-MRx中提供了用于屈曲设计的载荷设计系数,CC2676中提出一种基于弹性屈曲理论和等时应力应变曲线的蠕变屈曲设计方法,但只针对轴压圆柱壳。目前,ASME中并未提供针对一般结构的蠕变屈曲分析方法,RCC-MRx附录A7中提出简化分析方法,可进行所有壳体结构的蠕变屈曲设计。
(3)根据轴压圆柱壳屈曲算例可知,对于瞬时屈曲设计,ASME NH的结果最保守,RCC-MRx的非弹性分析方法次之,ASME NB方法最危险;对于蠕变屈曲设计,与CC2676相比,RCC-MRx中的简化设计方法更保守。
