共焦双曲柱面电极的电场及其数值模拟

王 福 谦

(西南交通大学 希望学院 基础部，成都610400)

0 引 言

由复变函数理论可知，解析函数的实部和虚部分别满足拉普拉斯方程，且其实部为常数和虚部为常数的两族曲线互相正交。在静电场中，解析函数的这一特性使其代表一定的平行平面场，其实部和虚部分别代表势函数(或通量函数)和通量函数(或势函数)。不同的解析函数的实部和虚部可描绘出不同的几何图形，如果某一解析函数所给出的几何图形与所讨论问题的边界的等势线或等通量函数线相吻合，则此解析函数的实部或虚部可作为待求势函数(或通量函数)和通量函数(或势函数)的解，即用此解析函数作为所求静电场的复势来求解电场分布。

复势函数法为求解复杂二维边值问题的一种有效方法[1-2]。文献[3-10]中利用复势函数法讨论了非平行板电容器电场、扇形导体中的电场、线电荷与无限大接地导体板间的电场及共焦椭圆柱电缆的磁场等复杂形状边界的静电场和静磁场的边值问题，但用该方法对复杂形状电极的电场分布的研究，相关文献还未见报道。本文利用复势函数法研究双曲柱面电极的电场，给出其电势分布、场强分布函数及电极顶点处的场强，讨论电极形状蜕变的几种特殊情形，并通过Matlab数据处理软件的数值计算功能进行数值模拟，绘制出其电场线和等势线图。

1 电势函数与通量函数

有一对共焦双曲柱面的电极，其实半轴和虚半轴分别为a1、a2和b1、b2，左侧电极接地，右侧电极的电势为U，其横截面如图1所示。因在垂直于双曲柱面母线的所有截面上的电场分布均相同，故本文所研究的电场为平行平面场。由于本文所讨论的二维边值问题的电势函数满足二维拉普拉斯方程，且其边界与反余弦函数实部所表示的曲线族中的曲线重合，故可选用反余弦函数作为所求静电场的复势[11]，即

W=Aarccos(z/k)+B

(1)

可进一步表述为

W=Aw+B=A(u+iv)+B1+B2

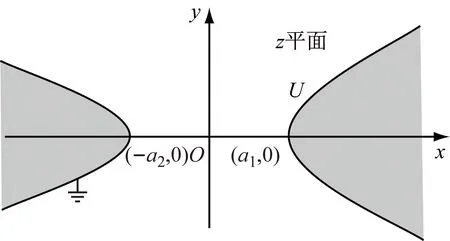
图1 共焦双曲柱面电极的横截面

令式(1)中的电势函数和通量函数分别为φ和Ψ，则

φ=Au+B1

(2)

Ψ=Av+B2

(3)

对图1右侧的双曲线顶点处(a1,0)，式(1)有：

U=Aarccos(a1/k)+B1

(4)

对图1左侧的双曲线顶点处(-a2,0)，式(1)有：

0=Aarccos(-a2/k)+B1

(5)

再者，由于式(3)中的附加常数可取任意值，故令

B2=0

(6)

由式(4)～(6)，可得：

故共焦双曲柱面电极电场的复电势为

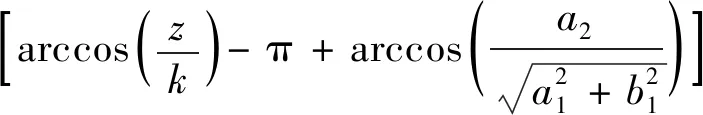
(9)

共焦双曲柱面电极电场的电势函数和通量函数可分别表示为:

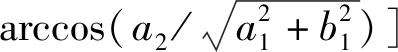
(10)

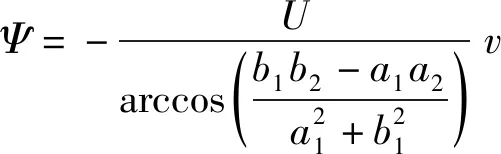
(11)

式(1)中的反余弦函数亦可表述为[12]:

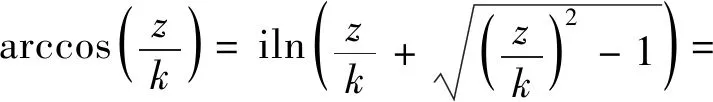
iln{x+F1cosα+i[y+F1sinα]}-ilnk=

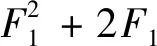
(12)

式中:

由式(12)得:

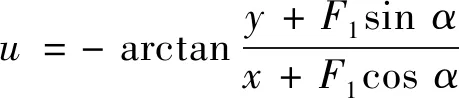
(13)

2F1(xcosα+ysinα)]-lnk

(14)

将式(13)、(14)分别代入 式(10)、(11)，可得共焦双曲柱面电极电场的电势函数和通量函数分别为:

(15)

2F1(xcosα+ysinα)]-lnk

(16)

2 场分布数值模拟及电极形状蜕变特殊情形

2.1 场分布的数值模拟

为了给出共焦双曲柱面电极电场分布图的直观图像，以验证本文所得结论的正确性,下面用Matlab对该电场分布进行数值模拟[13-15]，其电场线和等势线的分布见图2(取U=150 V)。由图2可见,图中的电场线与等势线及导体边界均垂直，场线分布正确，为预期结果。

2.2 电极形状蜕变的特殊情形

当共焦双曲柱面电极的实半轴和虚半轴取一些特殊值时，可得到几种特殊情形下的电场分布:

(1)双曲柱面电极的实、虚半轴的长度分别为5、0和4、3时，右双曲柱面电极蜕变为带电板，此情形的电场为水平带电平板与双曲柱面电极所形成(见图3)。

(3)左双曲柱面电极的实半轴和虚半轴的长度分别为0.01、5和5、0.01时，两双曲柱面电极蜕变为相互垂直的带电板，此情形的电场为双相互垂直的带电板所形成(见图5)。

(4)左、右双曲柱面电极的实半轴和虚半轴的长度均为5和0.01时，左、右两双曲柱面蜕变为共面平板，此情形的电场为共面带电平板为所形成(见图6)。

(5)左、右双曲柱面电极的实半轴和虚半轴的长度均为6和无限大时，左、右两双曲柱面蜕变为平行板，此情形的电场为大平行带电板所形成(见图7)。

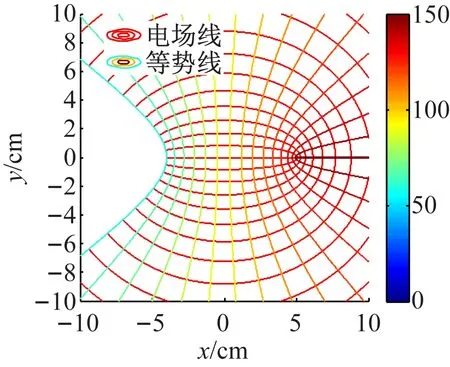
图3 带电板与双曲柱面的电极的电场

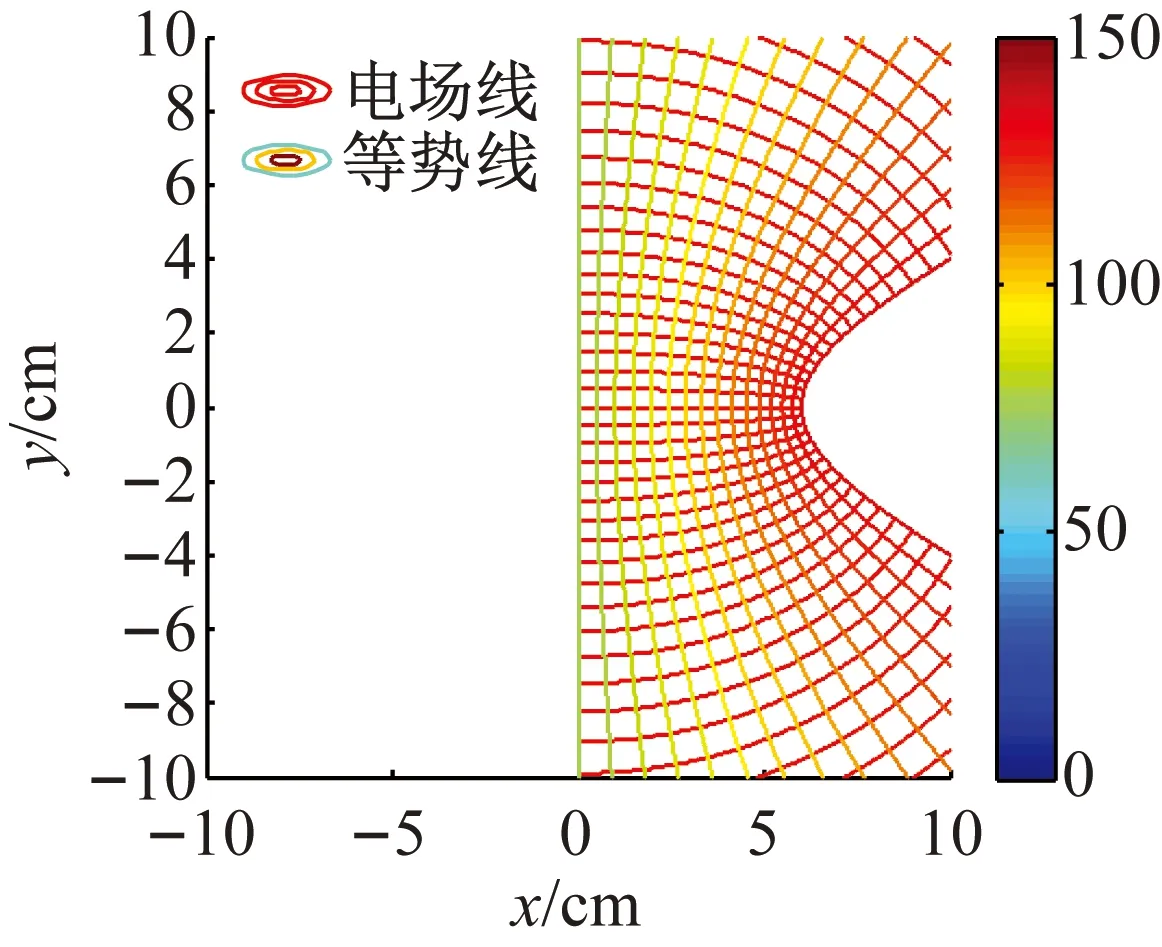
图4 双曲柱面的电极与带电板的电场

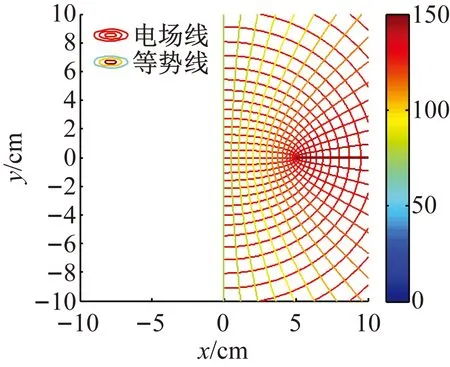
图5 两垂直不相连的带电板间的电场

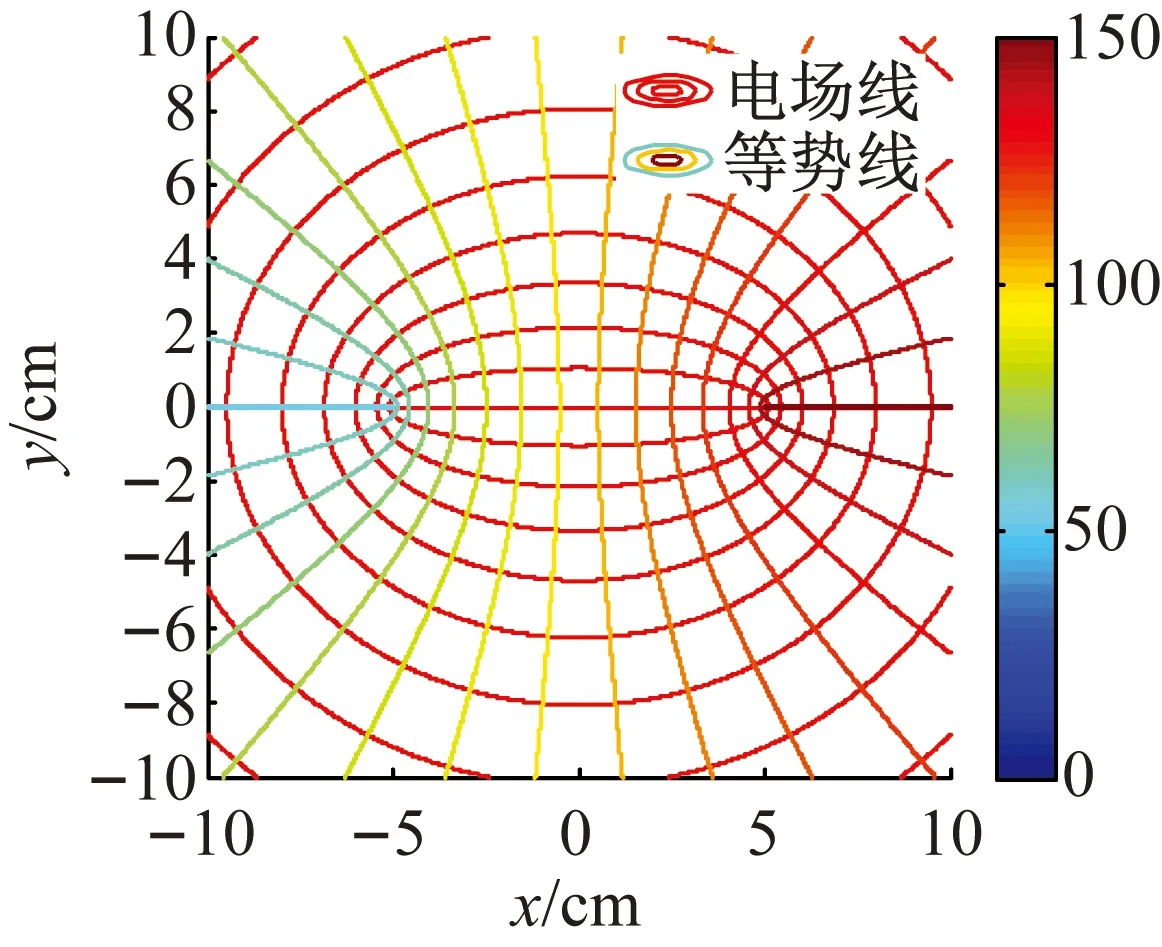
图6 两共面不相连的带电板间的电场

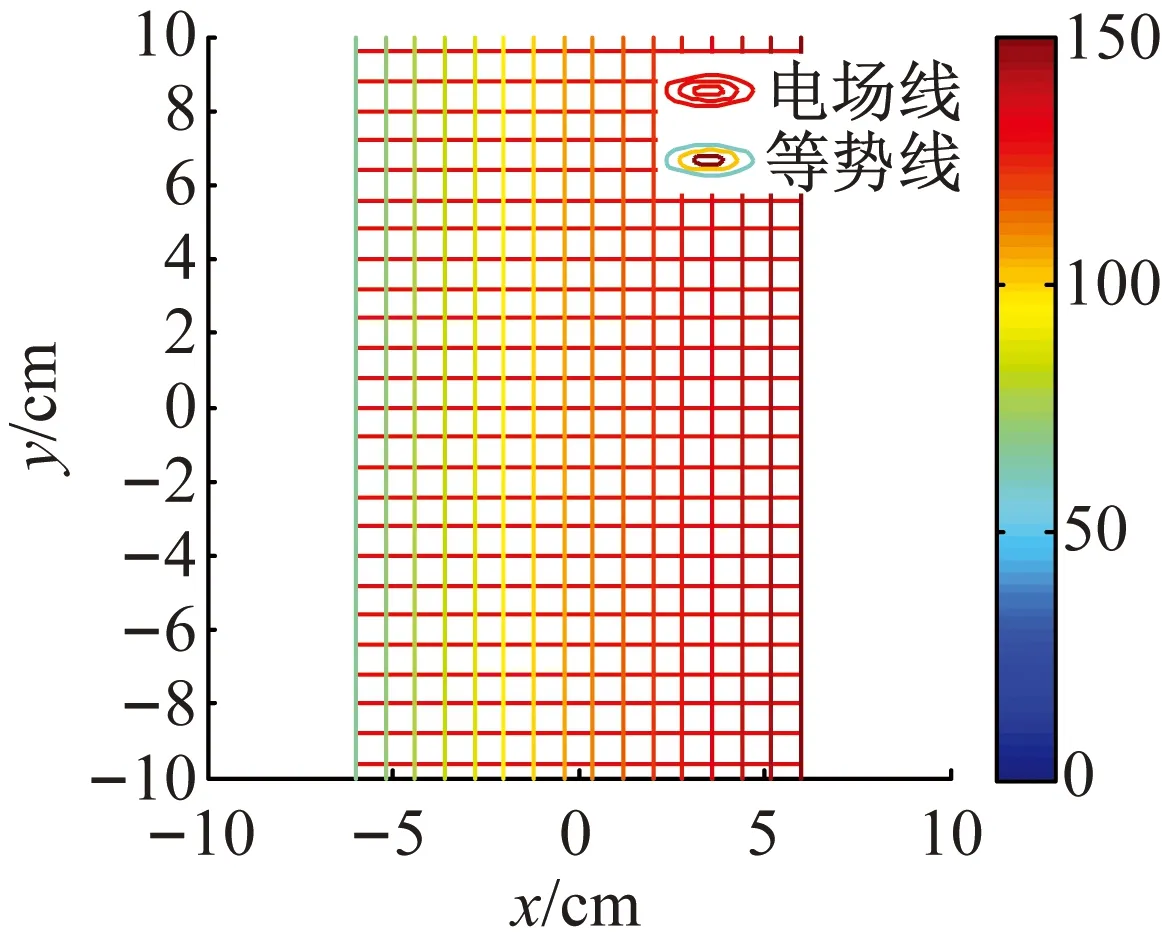
图7 平行带电板间的电场

所以，双曲柱面电极和带电平板所形成的电场、两相互垂直不相连的带电板所形成的电场、共面带电平板所形成的电场及平行带电板所形成的电场，均为本文所讨论问题的特例,本文的研究结论具有一定的普遍性。

3 电极场强分布及电极顶点处场强

由式(9)，根据电场强度与复势函数关系E=-[dW/dz]*，可得共焦双曲柱面电极电场的电场强度的复数形式为

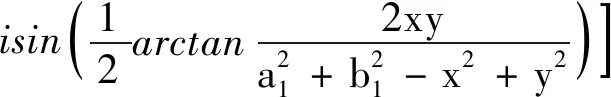
(17)

对于双曲柱面电极的两顶点处，其坐标分别为(a1,0)和(-a2,0)，将此两坐标值分别代入上式，则得双曲柱面电极的顶点处的场强大小分别为:

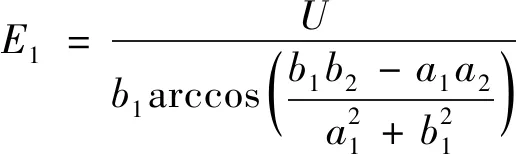
(18)

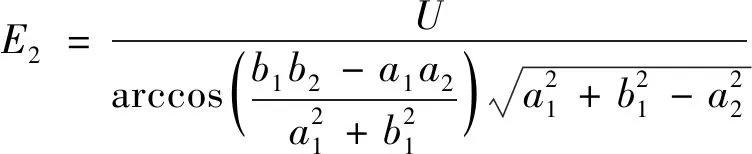
(19)

由表1可以看出：当双曲柱面电极顶点处曲率变大时，其附近的场强增大，而当双曲柱面电极的形状蜕变为两共面带电板时，其端头间的场强最强；当双曲柱面电极顶点处曲率变小时，其附近的场强减小，而双曲柱面电极的形状蜕变为两平行带电板时，其间的场强最小，且为匀强电场。

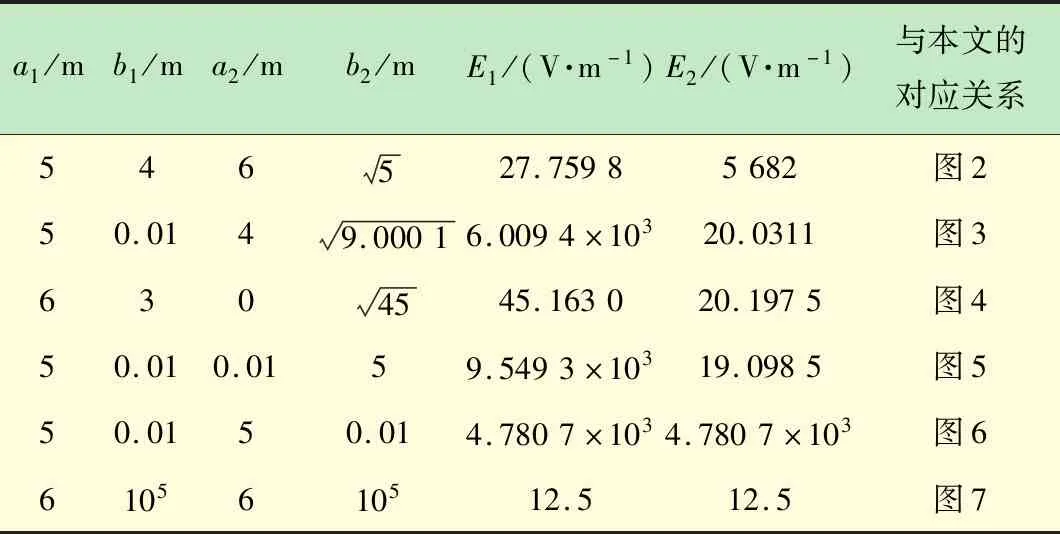
表1 双曲柱面电极顶点处的场强

4 结 语

本文将理论计算与数值模拟相结合，利用复势函数法研究研究双曲柱面电极的电场，得到了其电势分布和场强分布函数，并利用Matlab软件对场分布进行了数值模拟，给出了场分布的直观图像，为边界形状复杂的电极的电场分布问题的求解提供了一种新的方法，在科研上具有一定的理论意义和实用价值。