裂隙延展性统计分布离散性对岩体块体化程度REV的影响
2019-08-15于青春
夏 露,谢 娟,于青春
(中国地质大学(北京)水资源与环境学院,北京 100083)
表征单元体(representative elementary volume,REV)是裂隙岩体中重要的概念。对岩体来说,表征单元体的存在是应用连续介质力学方法对其进行研究的前提。正如只有当某岩体存在渗透表征单元体时,其渗透张量才有定义,才能够将多孔介质方法用于这一岩体。
由于岩体表征单元体概念的基础性,长期以来引起了众多学者关注。不同学者从不同角度对岩体REV进行了讨论。Bear从孔隙度的角度对岩体REV进行了研究[1];Long[2]、Wang 等[3]从渗透张量的角度讨论了表征单元体的存在性和尺度问题;张贵科等[4]从结构面几何参数和力学参数的角度以岩体内所有结构面在某截面上的投影面积之和与岩体体积的比值作为衡量岩体REV 尺度的指标;安玉华等[5]从岩体体积节理数收敛的角度来确定岩体的REV的大小;Xia等[6]提出了从岩体块体化程度的角度确定岩体REV。
块体化程度[7]是评价岩体完整性的一种指标,已有一些学者采用这一指标对岩体进行质量分级[8-10]。裂隙岩体的块体化程度指岩体中由裂隙圈闭形成的孤立块体的总体积在岩体中所占体积百分比,文献[6]从岩体块体化程度的角度对岩体REV存在性进行了较系统的分析。作者在文献[6]中,根据国际岩石力学学会的裂隙分级,针对7个延展性级别、11个间距级别建立了77种岩体结构模型。并对这77种岩体进行了块体识别,分别讨论了这77种岩体结构的块体化程度随着模型范围变化的波动情况。由于所建立的岩体结构模型是随机的,对每种结构的每个研究范围进行了多次随机实现。结果表明,对于所有的77种岩体,76种岩体的表征单元体的尺寸在2~20倍间距之间。然而在以往的研究中,作者简化裂隙模型,假设所有裂隙相互平行且大小相同。而实际岩体中裂隙数量众多,大小各异。块体是由裂隙相互交切圈闭而形成的,其几何特征自然受裂隙的几何特征的影响。裂隙大小与产状相结合影响岩石块体数量和规模,进而影响岩体的稳定性。因此,基于以往研究基础,本文讨论裂隙大小对形成块体的作用,使建立的岩体裂隙模型相对于以往研究的更一般化,更实际化。在文献[6]模型的基础上,首先,保持裂隙位置、产状、密度等其他参数不变,改变裂隙大小统计分布的方差;第二步,构建裂隙延展性统计分布的离散程度不同的三维裂隙网络模型;第三步,识别岩体中所有块体及其几何参数,绘制块体化程度与模型范围的关系图;最后,对各种裂隙岩体的块体化程度进行统计分析和定量计算,进而确定基于块体化程度统计的REV 存在性及其大小。
为了得到规律性的认识,本文选取最常见的裂隙延展性统计分布形式:正态分布。用其标准差来表达裂隙大小离散程度,利用课题组自主研发的软件General Block 软件[11]建立裂隙网络模型及块体识别计算,对得到的结果进行统计分析,从块体化程度这个角度,总结归纳裂隙延展性统计分布的离散程度对岩体REV的影响。
1 裂隙延展性统计分布
1.1 裂隙的三维形状及大小
若要建立三维裂隙网络模型,裂隙面在三维空间上的形状和空间分布是一个无法回避的问题。实际岩体中的裂隙面会是非常复杂的形状,即使是在很小的范围内所有的裂隙也极可能不是一个固定的形状。在不同的研究中,裂隙曾被假设为圆形、椭圆形、任意多边形等。一般来说,任意多边形、椭圆形假设由于含有更多的参数,可以更符合实际地描述野外的实际裂隙,但一个模型含有的参数越多,对野外数据的要求则更高。像椭圆模型,在野外如何确定椭圆长短轴的方向和大小就是一个很大的困难。因此无论是理论还是实际工程应用研究,目前绝大多数情况下都把裂隙看作是圆盘形,这样描述裂隙的大小只需要一个参数,即它的直径或半径。因此,本文采用空间位置分布满足均匀泊松过程的圆盘模型[12-13],这种模型是目前最为流行的裂隙模型,是许多裂隙参数统计理论建立的基础。这种情况下,裂隙面的延展性可以用圆盘的半径进行描述。
1.2 裂隙延展性及其统计分布
裂隙的延展性是表征裂隙系统的一个重要几何参数。文献[14-17]中可见,裂隙直径概率分布形式最常见的是服从正态分布(Normal分布)。如果随机变量X的概率密度函数为:
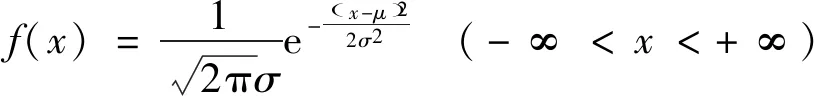
(1)
则称随机变量X服从正态分布,记作X~N(μ,σ2),其中μ与σ是分布的参数,参数μ是随机变量X的数学期望,参数σ是随机变量X的标准差。若固定μ,改变值σ,由f(x)的最大值可知,σ越大,正态密度曲线越平坦;σ越小,正态密度曲线越陡峭。参数σ决定曲线的形状(图1)。本研究中,裂隙延展性统计分布的离散程度即由标准差(σ)来表征。
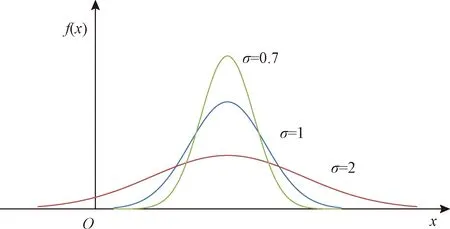
图1 正态分布概率密度函数曲线Fig.1 Curves of the probability density function of normal distribution
2 裂隙岩体块体化程度分析
2.1 裂隙网络模型
文献[6]中作者根据国际岩石力学会(1978)的岩体裂隙分级表,构建77种不同长度(D)、不同间距(C)的裂隙网络模型(表1)。由于计算量巨大,本文选取中间的模型即中等间距-中等延展性(MS1-MP1)模型(C=0.4 m,D=6.5 m)来进行详细分析讨论。模型的研究范围为长、宽、高相同的立方体,选取从2倍裂隙间距一直取到20倍裂隙间距:0.8,1.6,2.4,3.2,4,4.8,5.6,6.4,7.2和8 m。
根据3σ原则[18],随机变量x几乎落在区间[μ-3σ,μ+3σ]内,概率为0.997 4(图2),而落在该区间以外的概率可以忽略不计。因裂隙直径大于0,即μ-3σ>0,故本研究中对于每个模型范围,裂隙延展性统计分布选取5个不同标准差(σ=0.1,0.25,0.5,0.75,1)条件下的正态分布。
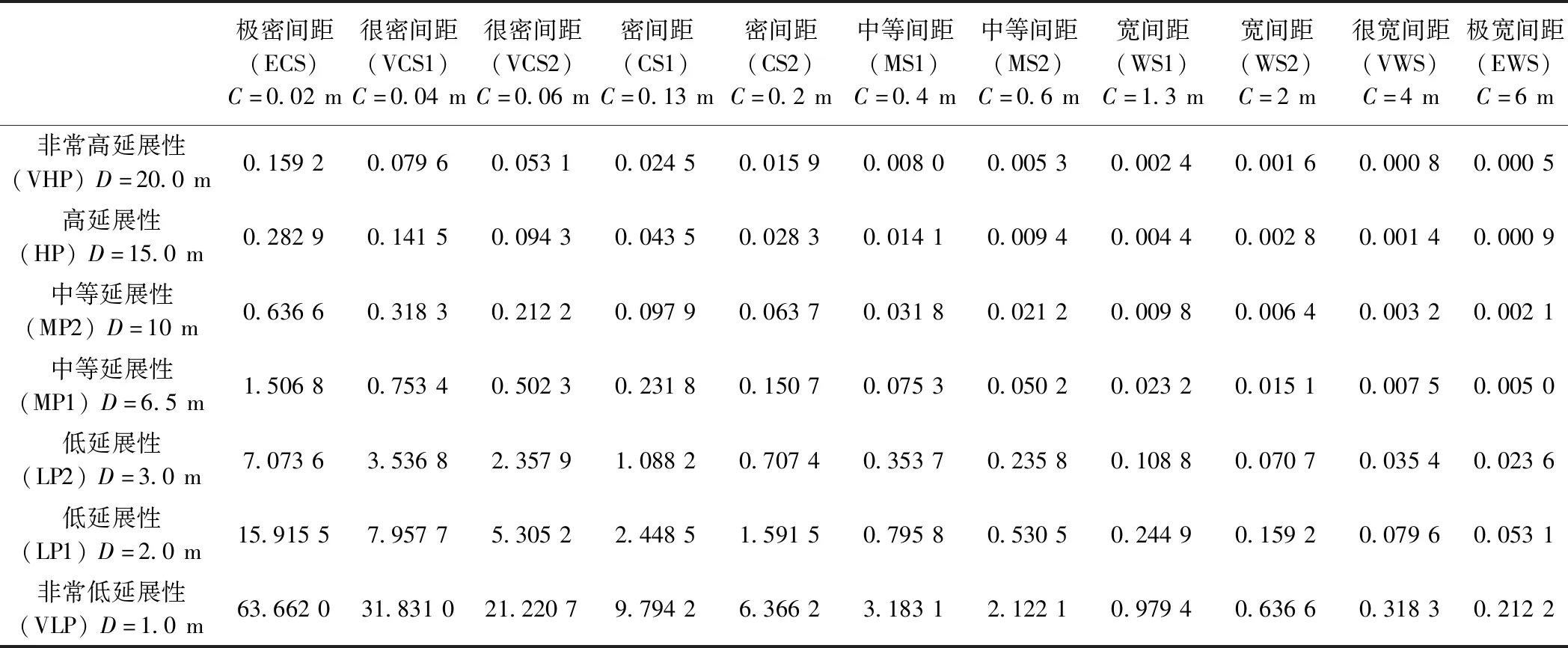
表1 77种裂隙岩体的裂隙间距、延展性、三维密度表(D=延展性;C=间距)Table 1 Spacing,persistence and three-dimensional density(d3)of the fractures in the 77 fractured rock models(D=persistence;C=spacing)
由于所建立的岩体结构模型是随机的,本文首先对每种结构的每个研究范围先进行9次随机实现,得到MS1-MP1裂隙岩体的块体化程度和REV值大小。然后再对研究范围为REV大小,即块体化程度达到稳定时,进行100次随机实现,得到模型的块体化程度。本文选取裂隙延展性统计分布为5个不同标准差条件下的正态分布,故文中共建立了1 005个裂隙模型,分别进行了块体识别并计算其块体化程度,归纳总结裂隙延展性统计分布的离散程度对岩体表征单元体的影响。
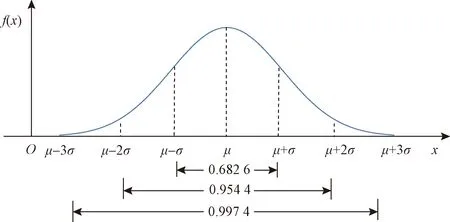
图2 正态分布μ两侧σ、2σ、3σ之间的概率Fig.2 Probability of σ,2σ,3σ on both sides of the normal distribution μ
中等间距-中等延展性裂隙网络模型具体参数如表2所示。图3是MS1-MP1裂隙岩体模型(模型范围:4 m×4 m×4 m)3种不同裂隙参数的三维裂隙网络图。图3a是裂隙延展性统计分布为标准差(σ=0.1)条件下的正态分布;图3b是裂隙延展性统计分布为标准差(σ=0.5)条件下的正态分布;图3c是裂隙延展性统计分布为标准差(σ=1)条件下的正态分布。
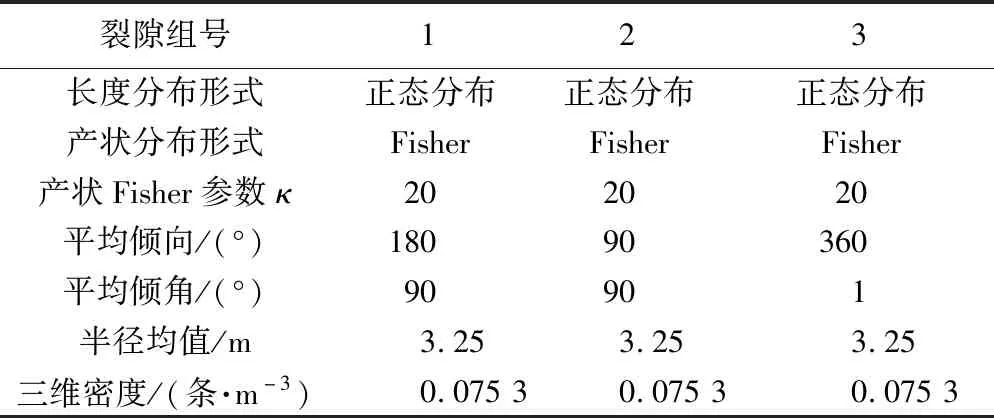
表2 中等间距-中等延展性裂隙网络模型参数表Table 2 Parameters for the discrete fracture network of the MS1-MP1 model
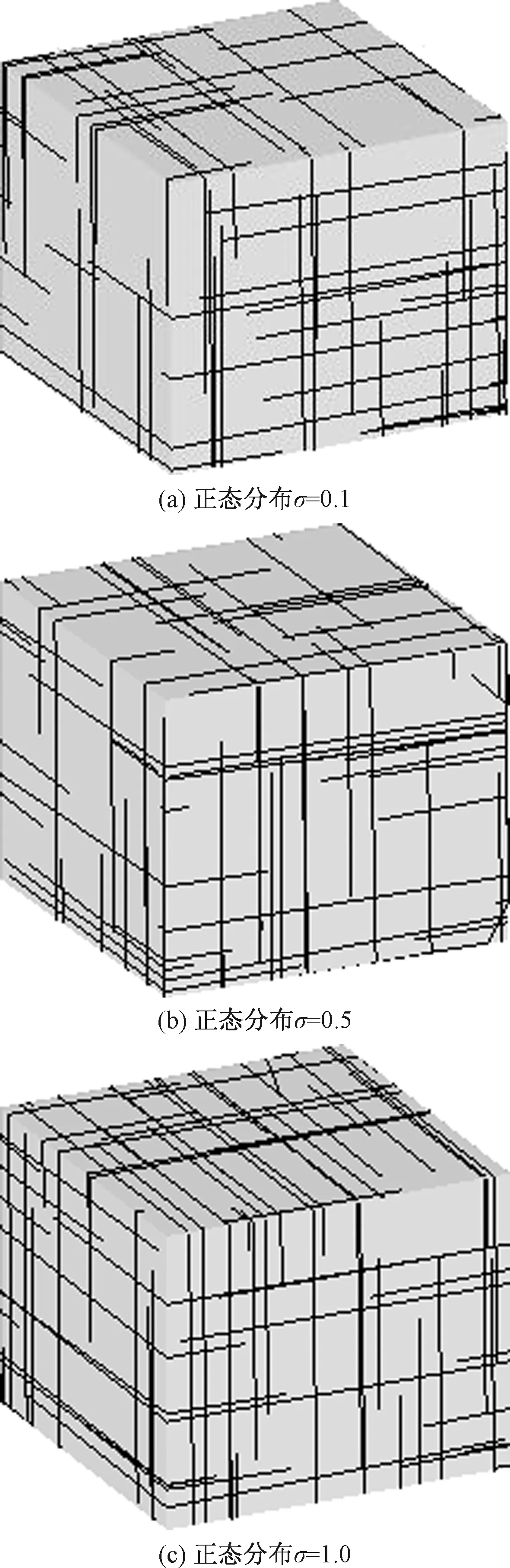
图3 中等间距-中等延展性裂隙岩体模型(模型范围:4 m×4 m×4 m)不同裂隙延展性统计分布离散程度的三维裂隙网络图Fig.3 3D fracture networks produced by different statistical distribution dispersions in the fracture size of the MS1-MP1 model(model dimensions:4 m×4 m×4 m)
对比设定的理想值与模拟值(表3)可发现,二者之间在裂隙半径均值、标准差、数量等方面都十分接近,说明建立的模型比较合理。
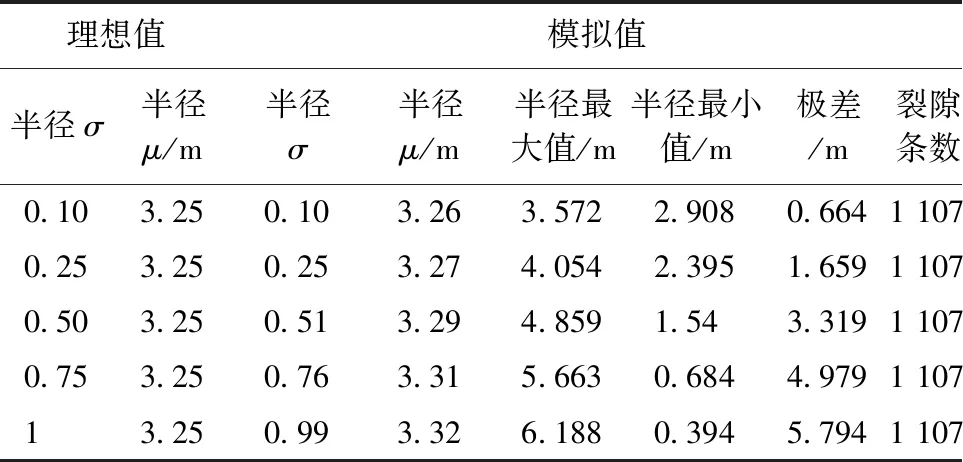
表3 中等间距-中等延展性岩体模型裂隙半径理想值与模拟值对比Table 3 Comparison between the theoretical and simulated of the fracture radius in the MS1-MP1 model
2.2 裂隙模型块体化程度计算
作者自主开发的General Block软件,它能够在“有限延展裂隙、复杂开挖面形状”条件下识别出所有块体,并得到块体的稳定性和几何参数,如块体体积、块体各顶点坐标等。用General Block 建立岩体模型,输入裂隙几何参数建立裂隙网络模型,对裂隙岩体进行块体识别及稳定性计算可以得到相关结果。用General Block软件建立中等间距-中等延展性裂隙岩体模型,并输入各组裂隙的随机参数(表3),进行三维裂隙网络模拟,并进一步进行块体识别计算。计算结果可以得到相应模拟的裂隙岩体中存在的所有块体及其几何参数。用块体百分比[6]来确定各不同裂隙岩体的块体化程度,进而来确定REV的大小。图4是图3中所示的3个模型的块体发育情况,图中的裂隙大小离散程度、间距及模型范围与图3相同。
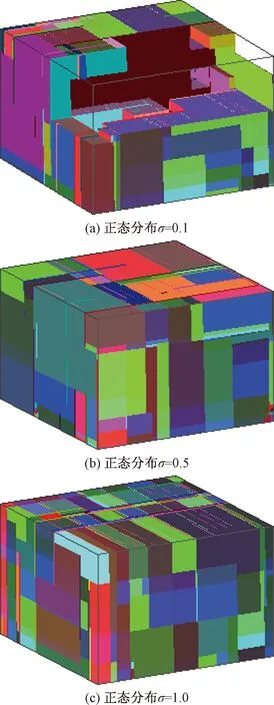
图4 不同裂隙延展性统计分布离散程度的中等间距-中等延展性裂隙岩体模型形成块体情况(模型范围:4 m×4 m×4 m)Fig.4 3D models of rock masses produced by different statistical distribution dispersions in the fracture size of the MS1-MP1 model(model dimensions:4 m×4 m×4 m)
3 裂隙大小离散性与REV的关系
3.1 裂隙大小离散性与岩体块体化程度的关系
利用General Block软件对中等间距-中等延展性模型中每个不同模型研究范围下的块体化程度进行计算统计分析。文献[6]中作者已得出中等间距-中等延展性裂隙岩体模型在研究范围达到10倍裂隙间距,岩体的块体化程度趋于稳定,即中等间距-中等延展性岩体模型的REV大小为4 m×4 m×4 m。由于所建立的岩体结构模型是随机的,为了得到裂隙大小离散性与岩体块体化程度的关系,减少随机性的影响,作者对此岩体模型研究范围4 m×4 m×4 m,裂隙延展性统计分布为5个不同标准差(σ=0.1,0.25,0.5,0.75,1)的正态分布条件下的裂隙网络模型,分别进行100次随机实现,绘制裂隙岩体的块体化程度随裂隙延展性统计分布离散程度的波动情况(图5)。图中纵轴(B)代表岩体块体化程度,即岩体中由裂隙圈闭形成的孤立块体的总体积在岩体中所占体积百分比;横轴(σ)表示裂隙大小的离散程度,即标准差(σ),图中的曲线表示的是100次随机实现的平均值。由图5可见,岩体的块体化程度随着裂隙延展性统计分布的离散程度增大而略有增加,其块体化程度从85.31%增加到90.96%。即随着裂隙延展性统计分布的离散程度变化,中等间距-中等延展性裂隙岩体模型的块体化程度稍有变化,其模型岩体处于相对破碎状态。这说明裂隙直径平均值一定的情况下,如统计分布的离散程度变化,岩体模型的块体化程度会略有上升,这方面有待于进一步详细研究。
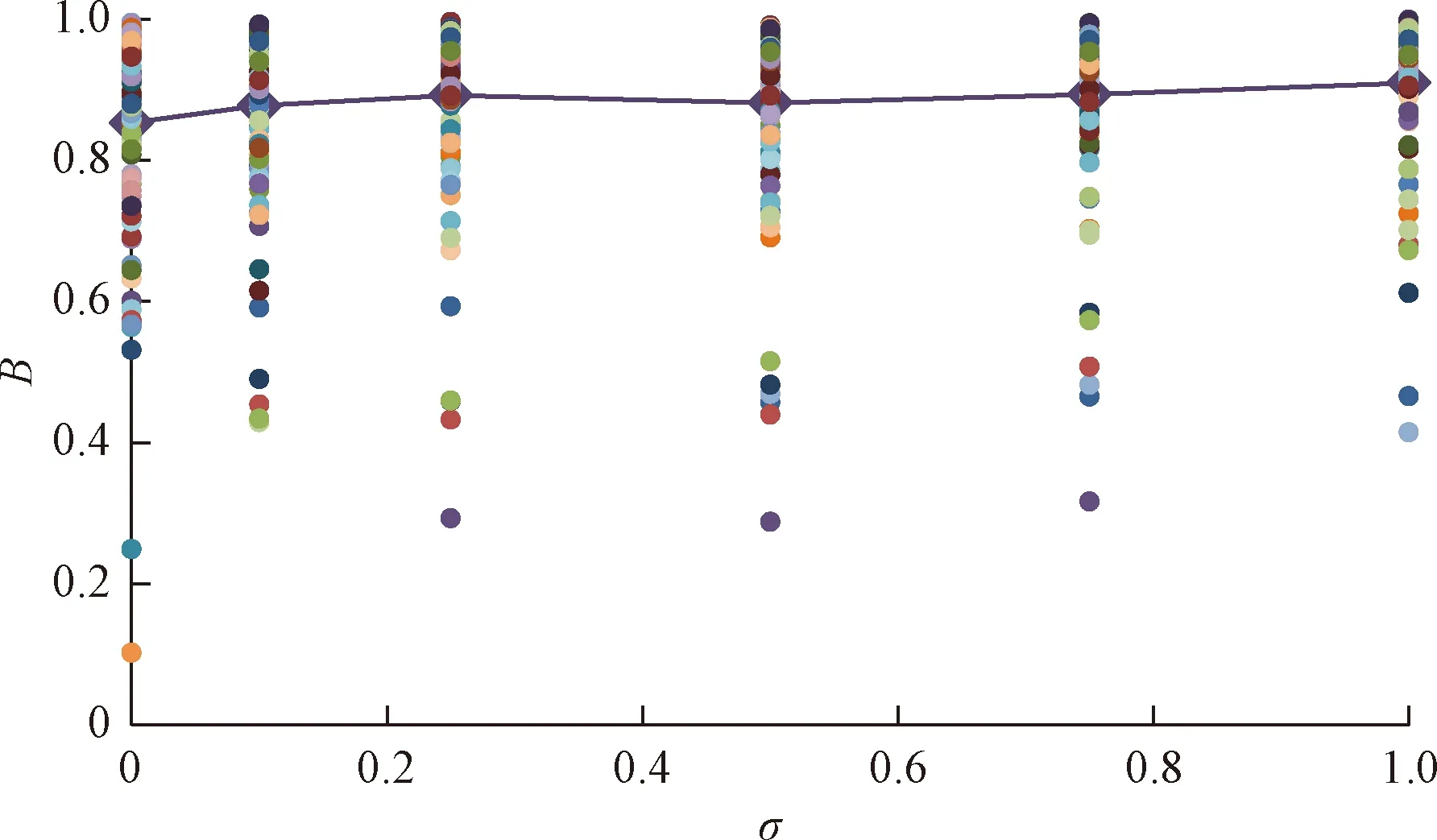
图5 中等间距-中等延展性裂隙岩体(模型范围:4 m×4 m× 4 m)B值与裂隙延展性统计分布离散程度(σ)的关系Fig.5 Relationships between B and statistical distribution dispersion in the fracture size(σ)of the MS1-MP1 model(model dimensions:4 m×4 m×4 m)
3.2 裂隙大小离散性与岩体REV值的关系
结合以上General Block软件的计算结果和相关的块体理论,绘制不同裂隙大小离散性条件下,岩体结构的块体化程度随着模型范围变化的波动图(图6)。图中纵轴是岩体块体化程度,横轴表示一个无量纲长度,研究范围长度L与裂隙间距C的比值。图中的5条曲线分别表示5个不同离散程度的裂隙延展性统计分布下,裂隙岩体块体化程度随模型范围的变化情况。如果把岩体模型的块体程度波动趋于稳定时的研究范围的长度定义为表征单元体的大小,那么可以初步认为,中等间距-中等延展性裂隙岩体的表征单元体的大小在10倍间距时,裂隙岩体的块体化程度达到稳定,中间的模型即中等间距-中等延展性模型(C=0.4 m,D=6.5 m),当裂隙直径平均值一定的情况下,其统计分布的离散程度变化,不影响其REV值的大小,中等间距-中等延展性模型的REV大小为4 m×4 m×4 m。

图6 中等间距-中等延展性裂隙岩体模型B值与模型范围的关系(C=0.4 m,D=6.5 m)Fig.6 Relationships between B and the model domain size of the MS1-MP1 model(C=0.4 m,D=6.5 m)
4 结论
(1)裂隙大小不变的条件下,中等间距-中等延展性裂隙岩体的块体化程度为85.31%。
(2)裂隙直径服从正态分布的情况下,如果其平均值一定,岩体的块体化程度随着统计分布离散程度的增加略有上升。
(3)中等间距-中等延展性裂隙岩体的REV值与裂隙延展性统计分布的离散程度相关性不大,其岩体的REV值为10倍间距,即4 m×4 m×4 m。
(4)以上结论是关于裂隙大小离散性与REV的关系的基本认识,假设裂隙大小满足正态分布。对于更复杂的分布形式仍有待于进一步研究。
