基于岩体结构特征和未确知测度评价模型的岩质开挖边坡稳定性研究
2019-08-15穆成林裴向军习朝辉
穆成林,裴向军,裴 钻,张 引,习朝辉
(1.四川师范大学工学院,四川 成都 610101;2.成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)
随着国家西部大开发和能源战略的深入推进,黔西地区的基础工程建设日益增多,其中层状岩质开挖边坡是最为常见的一项基础工程。层状岩质边坡在开挖过程中的变形失稳仍是亟待解决的问题,也是科学研究的重点和难点,其主要表现为:层状边坡的复杂岩体结构在差异性开挖条件下的变形失稳模式和机制具有多变性、多样性;边坡开挖前地质信息不完备导致传统稳定性预测结果出现较大偏差。
1993年,孙广忠教授[1]提出了岩体结构控制论的观点,认为变形失稳是岩体结构系统的失稳,不仅是材料的变形,更多情况下是结构失稳。孙玉科等[2]在岩质边坡稳定性分析中总结出“岩体结构分析的方法”,主张在边坡结构类型划分的基础上,以结构面与边坡的具体组合关系为依据分析边坡稳定性。
层状边坡岩体结构类型是控制变形失稳模式和机制的主要因素之一,是边坡评价的基础。Nicholson[3]分析了开挖岩体边坡结构类型和破坏模式,采用岩体质量为主要指标的稳定性评价;殷跃平[4]系统研究了三峡库区边坡结构类型,并对划分的5种典型边坡开挖前后变形破坏过程进行了研究;胡厚田等[5]在详细考虑红层边坡岩体的特征之后,甄选了4个对岩体结构和边坡稳定性影响最大的因素作为划分依据,将红层边坡分类,提出岩体结构的工程地质评价;周德培等[6]提出按坡体结构对边坡岩体进行分类,再由此建立计算分析模型进行岩质边坡的稳定性分析。
开挖岩质边坡的稳定性研究已有诸多成果。对于具体工程中边坡稳定性而言,已开挖边坡采用位移监测分析研究稳定性发展趋势较为理想,也实用可靠。非确定性分析方法在分析大量边坡稳定性中有明显优势。如,张军等[7]基于云模型理论,选取影响边坡稳定性的11 项指标,计算各指标隶属于不同岩质边坡稳定性等级的云模型数字特征,结合正向正态云模型和指标权重,计算待评估边坡的综合确定度,最终确定岩质边坡稳定性等级;李远松等[8]针对公路高边坡研究甄选坡体结构和评价因素,然后采用专家主观赋权和模糊计算模型对边坡进行稳定性评价;赵建军等[9]以汤口—屯溪高速公路44个典型边坡为研究对象,采用因子分析法,提出了边坡稳定性快速评价方法。以上研究成果为甄选边坡稳定性影响指标以及对指标的定性定量分级提供了宝贵经验。如果在此基础上对坡体结构进行合理分类并采用改进的指标赋权方法,将使边坡评价结果更为准确、科学。
本文以具有不同岩体结构类型的层状边坡在差异性开挖条件下的变形失稳模式、机制和稳定性预测为研究重点,通过对黔西地区高速公路、高速铁路以及工程场地开挖的124处层状岩质边坡系统的工程地质调查、统计分析,将岩体结构划分为4个大类、10个亚类,甄选12个稳定性评价指标,提出一种新的层状岩质开挖边坡稳定性研究思路:以边坡岩体结构类型为基础,建立组合赋权-未确知测度理论稳定性评价方法。
1 层状边坡岩体结构类型与特征
1.1 区域地质环境概况
黔西地区在大地构造上位于上扬子地台滇东—黔中隆起东部,处于特提斯构造域和滨太平洋构造域的结合部位,特殊的大地构造位置决定了其必然受到两者的共同作用,燕山期强烈的褶皱和断裂变形尤其复杂[10]。研究区边坡岩性主要为层状灰岩、白云岩、白云质灰岩、砂岩以及薄层状页岩、泥岩,且边坡岩体质量差异较大。
1.2 坡体结构类型划分主要因素
(1)岩性组合特征。岩性组合特征对边坡岩体的结构有重要影响[5]。地层岩性及组合是一个边坡基本地质结构框架,决定着边坡演化规律。地层岩性不同组合形式对边坡的演化模式、速度、规模特征及稳定性影响较大。常见地层岩性组合形式为层状硬岩、层状硬岩夹软岩、层状软硬互层、层状软岩夹硬岩、层状软岩。
(2)地质构造特征。层状岩质边坡除了层面以外,由地质构造作用形成的结构面特征对边坡变形失稳影响较大。通常缓倾层状岩体发育两组以上垂直(陡倾)层面的结构面,发育密集程度和延伸规模直接决定岩体质量;此外,岩体中发育的小断层、层间错动带以及长大构造裂隙使得边坡在开挖后发生不同失稳模式。地质构造作用同样使得边坡坡体中存在差异的应力效应,边坡开挖后,应力释放、岩体卸荷作用等致使边坡岩体劣化,整体稳定性渐进降低。
(3)软弱层(面)特征。层间软弱夹层(面)多为边坡变形失稳的滑移面(带),而其它裂隙软弱夹层(面)通常为变形失稳的侧边界或局部界面。软弱层(面)形成原因、空间的分布和延伸规律、力学效应及其与开挖边坡相对位置关系等是岩体类型中需考虑的重要因素[11]。
1.3 坡体结构类型及特征
参考相应规范[12-13]以及文献[5,14],结合上述层状岩质边坡结构类型划分主要因素,将黔西地区层状边坡坡体结构类型划分为4个大类、10个亚类(表1)。表中着重评价了各类型边坡工程地质特征,分析可能的失稳模式和形成机制,为进一步深入预测边坡稳定性打下了良好的基础。表1参考胡厚田等[5]分类评价,有修改。

表1 层状边坡坡体结构类型与特征Table 1 Rockmass structure styles and characteristics of the layered slopes
2 开挖层状边坡稳定性预测
边坡的稳定性预测主要是以坡体结构类型为基础,甄选影响边坡稳定性的控制性因素进行组合赋权,建立未确知测度评价模型。
2.1 组合赋权
以粗糙集改进层次分析法主观和熵值法客观权重形成的组合权的形式对边坡稳定性影响指标赋予权重,消除指标的差异性,使其符合真实情况。粗糙集改进层次分析法和熵值法的权重计算过程详见文献[15-19],不细阐述。
设粗糙集改进的层次分析法得到的权重为w′i,熵值法计算得到的权重为w″i,设两者的距离函数为d(w′i,w″i),其表达式为:
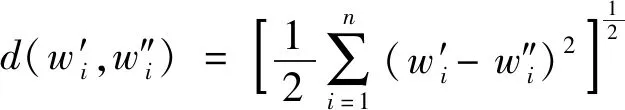
(1)
设组合权重为wi,则表达式为:
wi=αw′i+βw″i
(2)
其中,α,β为分配系数,其约束条件如下:
d(w′i,w″i)2=(α-β)2
(3)
α+β=1
(4)
2.2 未确知测度模型
(1)模型理论
假设被评价的边坡有n个,则待评价的边坡可以用空间向量集表示为:R={R1,R2,R3,…,Rn}。而对于每个待评价的边坡Ri(i=1,2,…,n)有m个单项评价指标空间:X={X1,X2,X3,…,Xn}。如果Xij代表边坡Ri的第j个评价指标的测量值,那么Ri={Ri1,Ri2,Ri3,…,Rim}。设每个指标Xij都有p个评价等级,即评价空间向量表示为:U={C1,C2,C3,…,Cp},并且设Ck(k=1,2,…,p)为第k级评价等级,k级比k+1级的稳定性差,记作Ck>Ck+1,若满足C1>C2>…>Cp,则称{C1,C2,C3,…,Cp}为评价空间U的一个有序分割类[16]。
(2)单指标测度评价矩阵
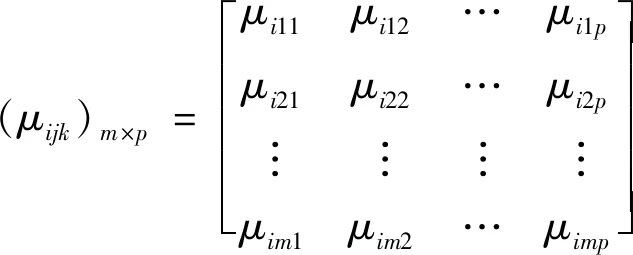
(5)
设μijk=μ(Xij∈Ck)表示测量值Xij属于第k个评价等级Ck的程度,若μ满足0≤μ(Xij∈Ck)≤1,且同时满足可加性和归一性准则,则称μ为未确知测度,简称测度。矩阵(μijk)m×p为单指标测度评价矩阵。
(3)多指标综合测度评价矩阵
令μik=μ(Ri∈Ck)表示边坡Ri属于第k个评价等级Ck的程度,则:
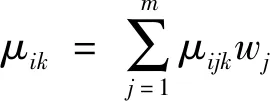
(6)
其中(i=1,2,…,n;k=1,2,…,p),wj为评价指标Xj在体系中所占的权重。多指标综合测度评价矩阵可表述为:
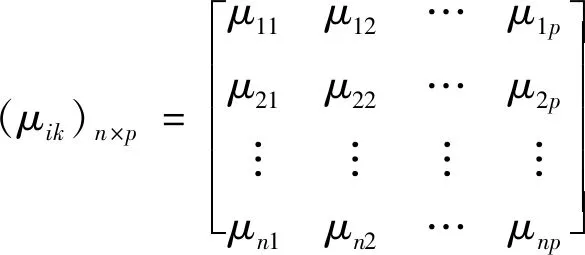
(7)
(4)置信度识别准则分析
采用置信度识别准则对待评价边坡进行稳定性等级预测。
若评价的空间U有序,且C1>C2>C3>C4>C5,设λ为置信度(常取λ≥0.5),则有式(8):
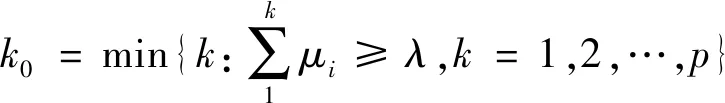
(8)
可以确定边坡Ri的稳定性属于第k0个评价等级Ck0。
2.3 评价体系和等级划分
开挖边坡稳定性指标涉及广泛且复杂,评价系统应具有系统全面、简单灵活、相对独立等特点,故选取指标应遵循以下原则:①科学性、目的性;②宏观性、实用性;③协调性、相对独立性。
(1)评价体系
以表1为基础,甄选影响边坡稳定性的主要因素为6个定性指标和6个定量指标(Xi),见表2~3。
(2)等级划分
将评价指标进行按稳定性进行等级划分及取值,评价集为{C1,C2,C3,C4,C5}依次代表边坡的稳定性:(Ⅰ级)极稳定、稳定(Ⅱ级)、一般稳定(Ⅲ级)、不稳定(Ⅳ级)、极不稳定(Ⅴ级),见表2~3。
2.4 构建单指标测度函数
根据上述单指标测度函数的定义和表2~3构建的单指标测度函数,求得各评价指标的测度值。其各自的单指标测度函数见图1~2。
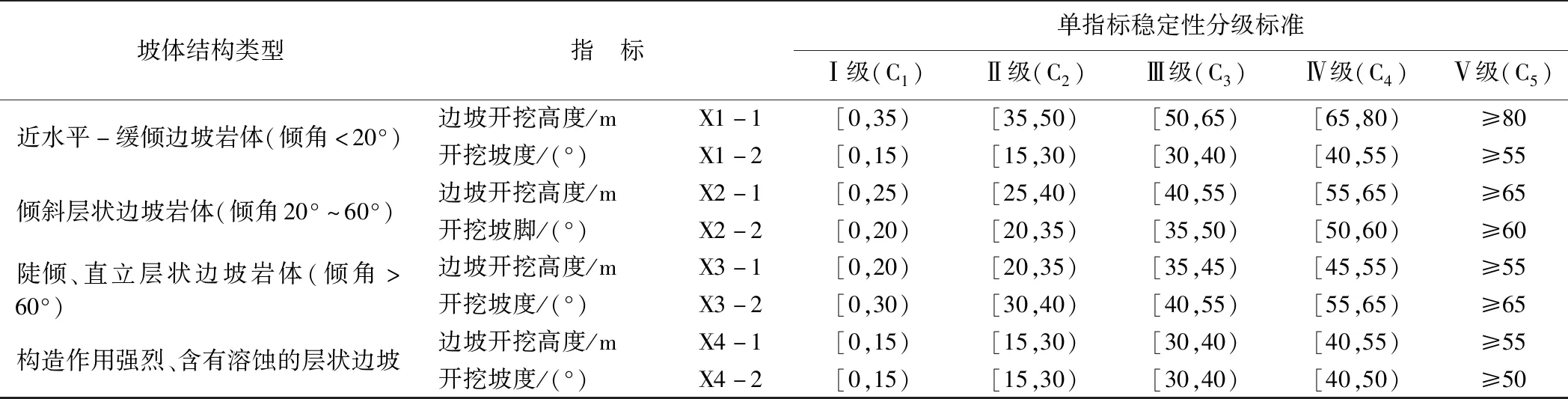
表2 层状边坡类型和指标评价等级Table 2 Types and influence indices grading standards of the layered slopes
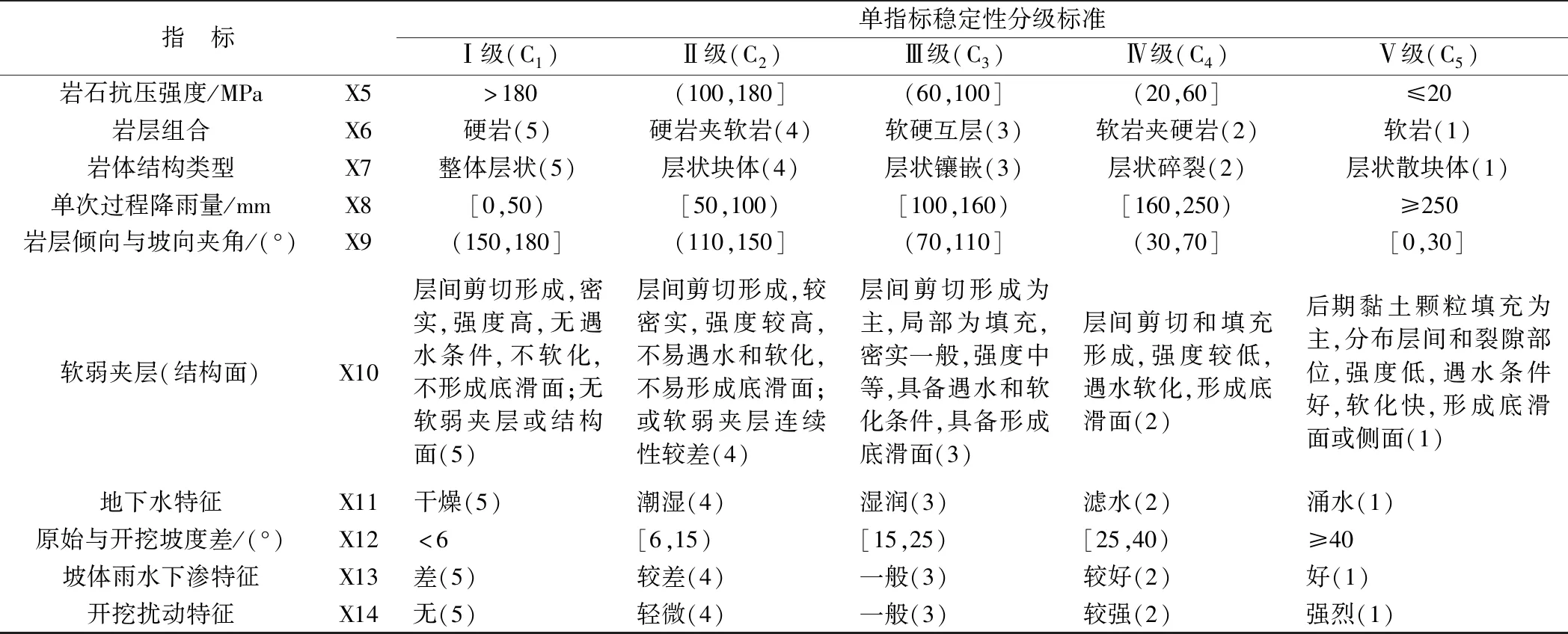
表3 层状边坡稳定性影响指标和评价等级Table 3 Influence index and grading standards of the layered slopes
注:X9按岩层倾向与坡面倾向在同一水平面上垂直法线投影的最小夹角原则取值,取值范围0~180°。
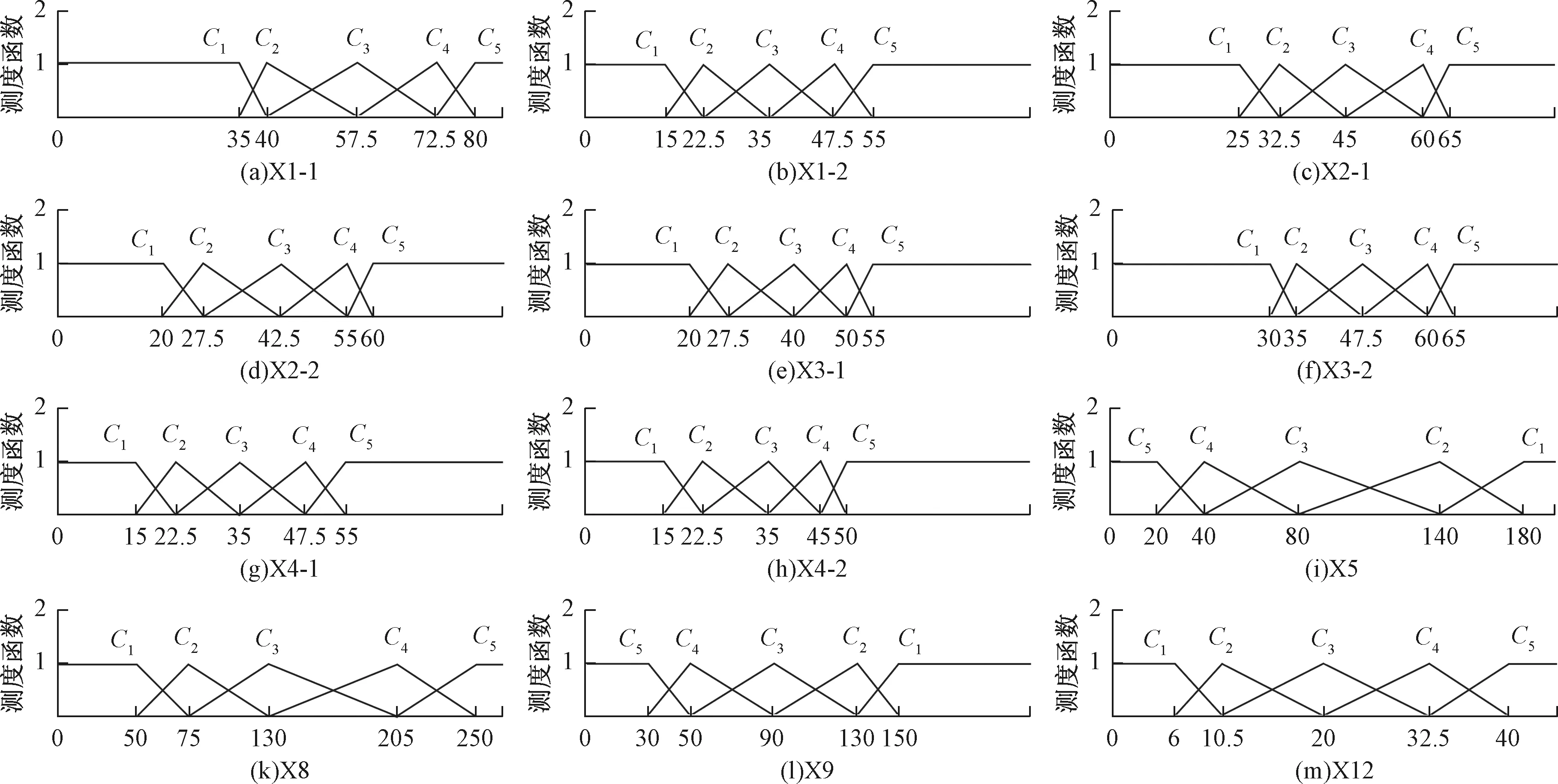
图1 定量指标测度函数Fig.1 Measurement function of quantitative indicators
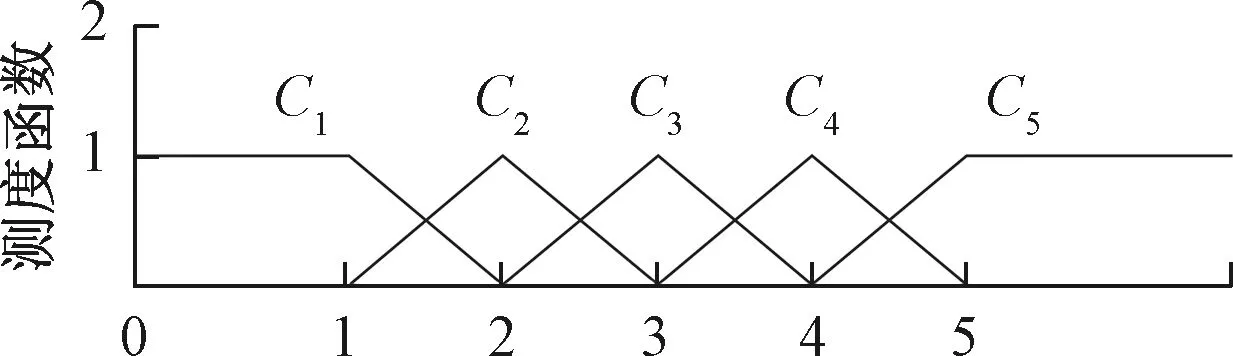
图2 定性指标测度函数(X6,X7,X10,X11,X13,X14)Fig.2 Measurement function of qualitative indicators (X6,X7,X10,X11,X13 and X14)
3 工程实例应用
3.1 开挖边坡工程地质概况
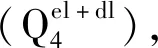
该边坡设计为采用爆破机械由上及下逐级开挖,每级高度为10.0 m,坡比为1∶1.0,坡向为正北,边坡总高度为58.6 m。据多年降雨统计,施工期间单过程降雨量平均为52.0~57.0 mm。
3.2 开挖边坡稳定性预测
(1)岩体结构类型及特征分析
工程地质评价:对照表1,P1边坡结构属于Ⅱ类(Ⅱ-Ⅰ亚类)顺层岩质边坡。根据岩层倾角24°,设计开挖坡度45°和高度50 m,层间含有软弱夹层且易遇水软化等方面的特征分析:边坡在降雨工况下,稳定性较差,易发生沿层间软弱夹层的滑移-拉裂模式失稳破坏。
(2)组合赋权-未确知测度预测
以上述粗糙集层次分析法主观权重、熵值法客观权重分析理论为基础,通过式(1)~(4),计算实验P1边坡指标的组合权重值结果见表4。
根据单指标测度函数定义,结合表1、图1~2,构建单指标测度函数矩阵:
(9)
结合式(9)单指标测度矩阵及公式(6)~(8),可求得P1边坡多指标测度评价向量:{0.081 4,0.115 0,0.391 8,0.314 3,0.097 4}。取λ=0.5,从大到小:0.081 4+0.115 0+0.391 8=0.588 3>λ=0.5,则判定P1边坡稳定性等级为C3;按从小到大:0.097 4+0.314 3+0.391 8=0.803 5>λ=0.5,同样判定P1边坡稳定性等级为C3。
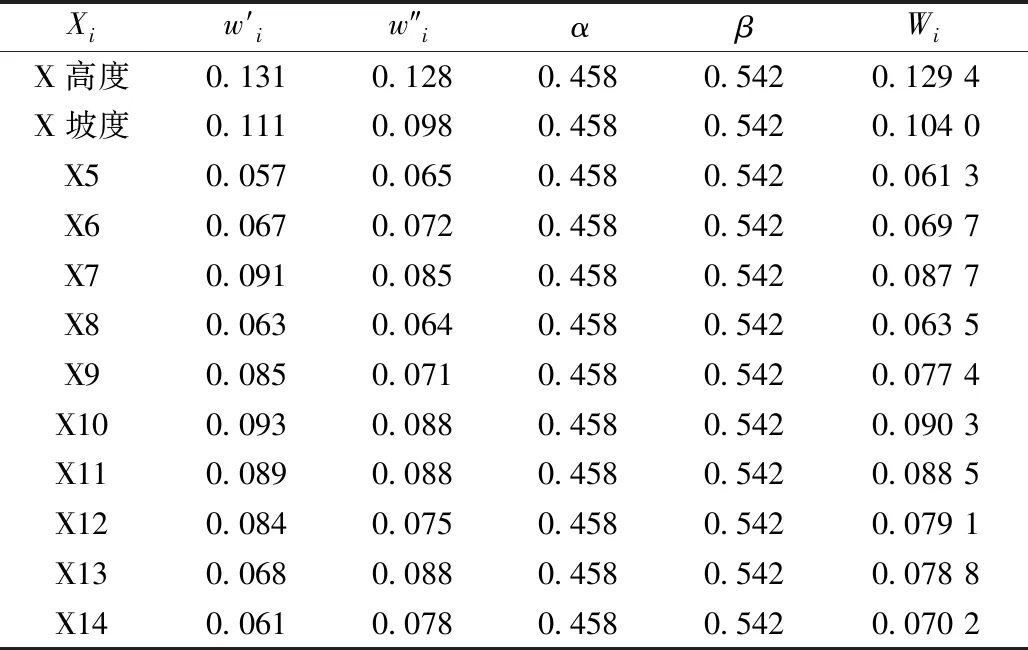
表4 影响指标组合赋权值Table 4 Combined weight of influence indicators
(3)P1边坡变形失稳过程
边坡于2014年10月28日开始进行爆破施工。2014年12月10日形成高度约44.4 m的边坡。在经历单程降雨(54.6 mm)后,边坡于20日发现开始发生变形:首先在四级台阶下方顺坡面3.4 m部位沿层间软弱夹层剪出,坡表出现拉裂缝。随着时间的推移,拉裂缝由下及上逐级出现,失稳边坡最终形态呈簸箕状。变形发生后在坡脚回填反压大量碎石进行坡脚反压防护,直至2015年2月15日后变形暂时稳定,见图3。
3.3 其它边坡稳定性预测
(1)以现场调查为基础,室内外岩土体力学实验为依据,拟开挖8个边坡指标评价取值见表5;稳定性预测结果见表6。
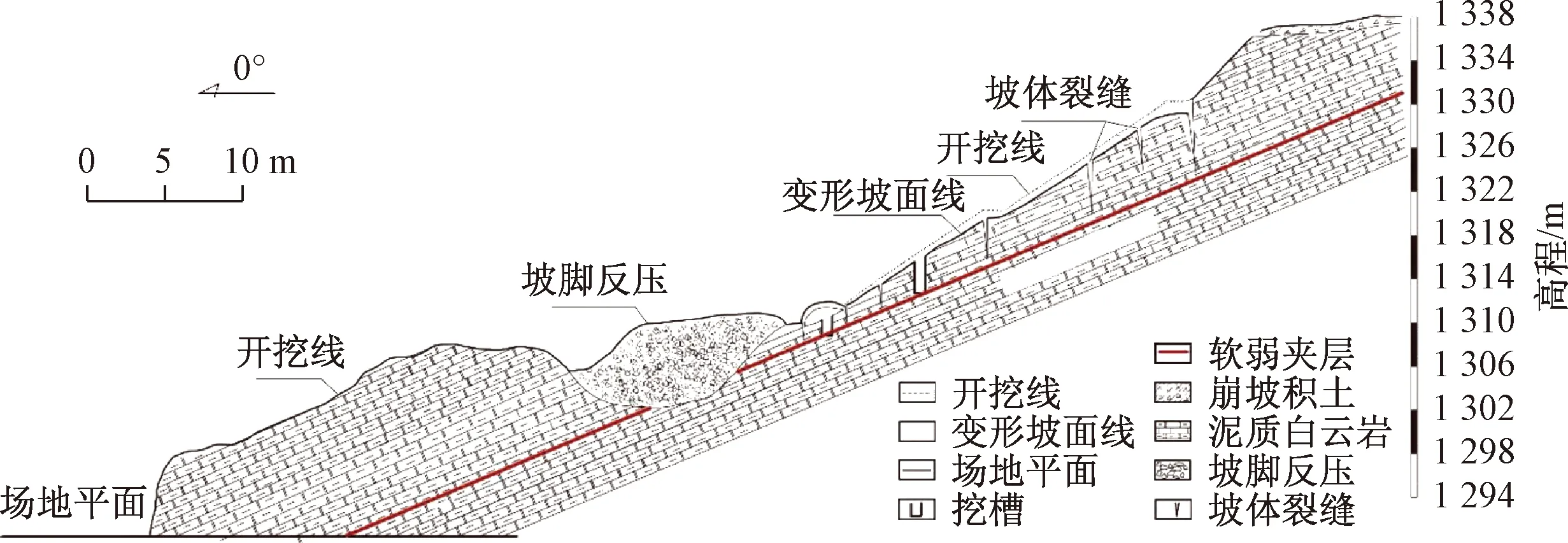
图3 P1边坡工程地质剖面图Fig.3 Schematic engineering geological profile of the P1 slope
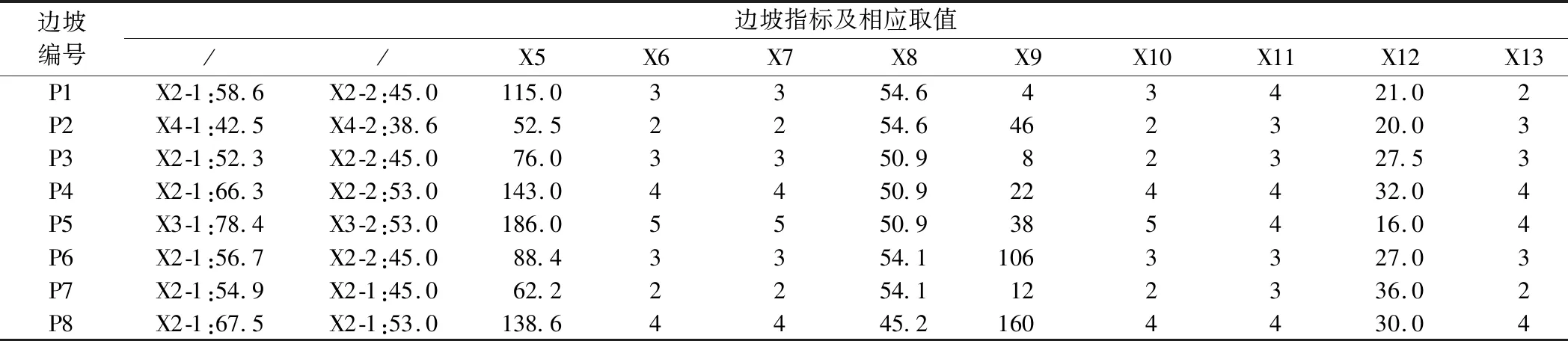
表5 层状边坡稳定性影响指标和取值Table 5 Influence index and the values of the layered slopes

表6 层状边坡稳定性预测等级Table 6 Grading standards of stability of the layered slopes
(2)边坡的过程地质评价与本文的稳定性预测结果一致,但与模糊评价结果(边坡P3、P7)存在差异。经过边坡开挖后监测、调查表明本文评价结果与实际相符。反复分析后,认为模糊评价等级较高的原因是未充分、客观考虑边坡岩体结构特征对稳定性的影响。
4 结论
(1)通过对黔西南地区大量层状岩质开挖边坡的调查,主要按岩层倾角将岩体结构类型划分为4个大类、10个亚类型,并针对相应类型边坡进行工程地质综合评价,阐述了失稳模式和机制。
(2)以层状边坡岩体结构类型为基础,选定12个边坡稳定性的影响指标,包括6个定性指标和6个定量指标。建立单指标测度函数,采用组合赋权值构建多指标测度矩阵,并将边坡稳定性分为5个等级,利用置信度对边坡稳定性进行识别,建立层状边坡稳定性分级的未确知测度评价模型。
(3)对8个层状边坡进行工程地质评价,采用构建的预测模型进行验证,并与模糊评价结果比较,结果表明:本文稳定性评价模型科学合理,准确度较高,评价结果与实际情况一致,计算过程相对简单易懂,可以在实际生产中指导施工、支护等工程。
(4)将未确知数学理论应用到层状开挖边坡稳定性预测中,构建稳定性的未确知测度模型,能够得出实际工程各边坡稳定性的等级,这丰富了边坡稳定性分级的预测方法,具有一定的应用意义。
