基于MEMS传感器的道面坡度提取方法*

苏志刚,吴柳莉,郝敬堂

(1.中国民航大学 智能信号与图像处理天津市重点实验室,天津 300300;2.中国民航大学 中欧航空工程师学院,天津 300300)

由惯性测量单元(Inertial Measurement Unit,IMU)组成的惯性导航系统(Inertial Navigation System,INS)可以精确地定位车辆的水平位置,但对高度和坡度的测量需额外的辅助传感器提供辅助参数[1]。在车辆行驶过程中若遇到上下坡以及不同坡度的高架桥路面时,导航系统便有可能产生较大的估计偏差。如何较为精确地实现对高度位置和道面坡度的解算,引起业界学者的广泛关注。

国内外道路坡度识别的方法可从实现原理上分为三类:基于全球定位系统GPS(Global Positioning System)数据的方法、基于车辆动力学模型的方法和基于加速度估计的方法。基于GPS数据的方法,其测量精度取决于GPS的有效使用范围[2],且易受遮挡物的影响。基于车辆动力学模型的方法是建立车辆与道路坡度之间的动力学关系模型[3],其对传感设备精度要求较高[4]。基于加速度估计的方法是利用加速度传感器估计车辆的俯仰角,并提取道路坡度信息[5]。基于加速度估计的方法采用的加速度传感器大多是便携式微机械电子系统(Micro-Electro-Mechanical System,MEMS)传感器。该类传感器采集的数据精度较低,噪声干扰相对较大[6],且在解算过程中需要对加速度进行积分处理,引入了累积误差的问题,同时,在进行坡度提取时一般需要解算运动加速度。因此,此类方法通常需额外的辅助传感器提供辅助参数。Jang J H等利用轮速传感器采集的车辆速度数据,并据此解算出轨迹信息[7],Son Y等采用气压传感器来获得道路的绝对高度信息[8],高婷婷等采用里程仪通过建模得到坡度[9],Norrdine A等利用置于足底的传感器检测行人行走过程中脚触地时短暂的零速状态实现对累积误差的修正[10]。

本文采用MEMS传感器实现对道面坡度的提取,在不增加额外传感器的基础上,利用零加速修正方法解决了惯性平台的误差累积问题,并提出了一种新的坡度提取方法,根据重力向量在载体坐标系中的变化实现对道面坡度信息的解算。

1 算法框架

利用智能手机中三轴加速度计、三轴角速度计和三轴磁力计构成测量平台,将智能手机固定在运动平台上,即运动平台与智能手机的相对位置关系不变。运动平台在道面上运动时,道面坡度对运动平台的影响将直接引起智能手机相对初始状态的变化,利用智能手机中各个传感器的实时数据即可实现对道面坡度信息的解算。

道面坡度提取算法的结构如图1所示,由数据采集、零加速状态检测、旋转四元数估计和位置解算与坡度提取等四部分组成。

图1 算法框图

数据采集是利用三轴加速度计、三轴角速度计和三轴磁力计获得智能手机实时的加速度、角速度和测量当地的磁分量数据,这些数据均以载体坐标系的形式进行表征。在进行道面坡度提取过程中,另外两个被涉及的坐标系分别是地理坐标系和导航坐标系,三个坐标系的关系如图2所示。载体坐标系是以载体手机质心为原点,平行于手机短边、长边和垂直于手机屏幕向上的方向而建立的坐标系ObXbYbZb(b系)。以道面坡度提取起点为参考点的东北天(ENU)坐标系被定义为地理坐标系。平行于地理坐标系各坐标轴,并与载体坐标系共原点建立导航坐标系ObXnYnZn(n系)。

图2 坐标系之间的关系

零加速状态检测将利用实时的加速度和角速度数据进行判断智能手机是否处于零加速状态。旋转四元数估计则是根据零加速状态检测的结果更新旋转四元数的估计,若手机处于零加速状态,则根据零加速状态的特点进行旋转四元数初始化;若手机处于非零加速状态,则根据前一时刻的旋转四元数进行更新处理。位置解算与坡度提取部分则是根据当前的旋转四元数数据及传感器的实时数据对手机的位置进行更新,并提取此时的坡度信息。智能手机的位置信息及道面坡度信息均是在地理坐标系中表征。

2 零加速状态检测

零加速状态就是智能手机处于平动加速度和转动加速度均为零的受力平衡态。此时,虽然速度可能不为零,但载体坐标系与导航坐标系间的位置关系相对固定,可以进行旋转四元数初始化,从而实现对惯性器件累积误差的修正。

在零加速状态时,理论上三轴加速度计的输出为重力加速度的值,三轴角速度计的输出为零,但由于噪声的存在,在进行零加速检测时,需要对三轴加速度计采集的载体坐标系的加速度向量ab(t)=[axtaytazt]T和三轴角速度计采集的角速度向量ωb(t)=[ωxtωytωzt]T进行范数阈值判决。

利用ab(t)进行加速度检测。

其中‖·‖表示向量的范数,thamin与thamax为加速度向量ab(t)的范数的上、下阈值。

利用ωb(t)进行角速度检测。

其中,thωmax为角速度向量ωb(t)的范数的阈值。

如上所述,同时满足以上两种条件时判定为零加速状态,即:

T(t)=T1(t)×T2(t)

(3)

3 旋转四元数估计

零加速状态检测模块输出的结果有两种可能,即检测出智能手机处于零加速状态或非零加速状态。若智能手机处于零加速状态,则将根据零加速状态的特点对旋转四元数初始化;若手机处于非零加速状态,则将根据前一时刻的旋转四元数进行旋转四元数更新。

3.1 旋转四元数初始化

当智能手机处于零加速状态时,载体坐标系与导航坐标系之间的位置关系保持不变,此时可以利用传感器采集的数据直接实现对旋转四元数进行初始化,从而消除前期累积误差的影响。

根据图2定义的坐标系之间的关系,载体坐标系到导航坐标系的变换可以看作载体坐标系绕导航坐标系定义的某单位向量un(t)=[uxtuytuzt]T逆时针旋转ϑnt角度得到导航坐标系。因此,载体坐标系下三轴加速度计输出gb(t)=[gxtgytgzt]T和三轴磁力计输出hb(t)=[mxtmytmzt]T也可绕单位向量un(t)逆时针旋转ϑnt角度得到导航坐标系的重力分量gn=[0 0 -g]T和磁场分量hn=[hxhyhz]T,其中g为当地重力加速度,hx、hy和hz为当地磁力线在地理坐标系的各轴向的分量,可由国际地磁参考场IGRF(International Geomagnetic Reference Field)获得。由此可知,向量un(t)一定位于gn和gb(t)之间的对称面上,该对称面的法向量为:

r1(t)=[gxtgytgzt+g]T

(4)

同理,un(t)也一定落在hn与hb(t)之间的对称面上,相应对称面的法向量为:

r2(t)=[mxt-hxmyt-hymzt-hz]T

(5)

所以,un(t)位于式(4)和式(5)定义的两平面的交线上,该交线的方向向量:

ul(t)=r1(t)×r2(t)

(6)

由此可得ul(t)在导航坐标系各轴向的分量:

ulxt=gyt(mzt-hz)-(gyt+g)(myt-hy)

(7)

ulyt=(gzt+g)(mxt-hx)-gxt(mzt-hz)

(8)

ulzt=gxt(myt-hy)-gyt(mxt-hx)

(9)

对方向向量ul(t)进行归一化计算:

即可求得单位向量un(t)的三个分量uxt、uyt和uzt。

利用单位向量un(t)和旋转角度ϑnt可构成四元数[11]:

其中,i,j和k是虚数单位。显然范数‖qn(t)‖=1。

假设载体坐标系中的向量rb(t)=[xbtybtzbt]T在导航坐标系中的对应向量为rn(t)=[xntyntznt]T,定义p(·)为将三维向量映射为纯四元数的函数,则有:

p[rb(t)]=xbti+ybtj+zbtk

(12)

p[rn(t)]=xnti+yntj+zntk

(13)

式(12)和式(13)中四元数间关系为

对式(14)进行逆运算可获得由导航坐标系向载体坐标系的映射关系:

将gn和gb(t)代入式(15)并整理得

-gxt/g=(1-cosϑnt)uxtuzt-uytsinϑnt

(16)

-gyt/g=(1-cosϑnt)uytuzt+uxtsinϑnt

(17)

(18)

由式(18)可得:

将式(19)可得代入式(17)并整理得:

根据式(19)和式(20)即可确定ϑnt所在象限及其值。

利用获得的un(t)的各个分量uxt、uyt、uzt与ϑnt,由式(11)可确定四元数qn(t)。

3.2 旋转四元数更新

当智能手机处于非零加速状态时,三轴加速度计的输出将不再影响载体坐标系与导航坐标系之间的位置关系,而是三轴角速度传感器采集的数据向量ωb(t)影响载体坐标系与导航坐标系之间的位置关系。因此,利用ωb(t)实现对旋转四元数的更新。

如前所述,旋转向量un(t)和旋转角度ϑnt均是在导航坐标系定义的,因此,由un(t)和ϑnt所确定的旋转四元数qn(t)也是在导航坐标系下定义的。对旋转四元数qn(t)的更新需要利用导航坐标系的角速度向量ωn(t)。根据式(14)可得:

在时刻t旋转四元数qn(t)的变化率为:

因此,相应的旋转四元数qn(t)的更新为:

4 位置解算与坡度提取

根据获得的旋转四元数qn(t)和传感器采集的数据进行平台位置的解算和道面坡度信息的提取。假设平台由静止状态开始,则在初始状态下,导航坐标系的加速度向量an(0)、速度向量vn(0)和位置向量pn(0)均为零向量,根据此时的零加速可以获得旋转四元数qn(0)。

在平台运动过程中,平台所获得的加速度向量ab(t)为载体坐标系中的测量值。当进行坡度测量过程中需要将ab(t)进行坐标变换,并用重力加速度向量gn进行补偿[12],从而获得导航坐标系形式an(t)。参考式(14)可得:

速度向量的更新方程为:

v(t+dt)=v(t)+an(t)dt

(25)

其中,v(t)为当前时刻的速度向量,v(t+dt)为速度的更新值。当载体处于零加速状态时,加速度an(t)为零向量,则式(25)变为:

v(t+dt)=v(t)

(26)

位置向量的更新方程为:

p(t+dt)=p(t)+v(t)dt

(27)

其中,p(t)为当前时刻的位置向量,p(t+dt)为位置向量的更新值。位置向量p(t)的垂直轴向的分量即为平台相对起始时的相对高度。

常规的倾角仪测量道面坡度的方法,是当载体静止或以恒定速度运动时,采用安装在载体上的三轴加速度计测量重力加速度分量,通过各轴向测量信息与重力加速度之间的关系可获得坡度信息。若是载体处于变加速运动时,则需要采用额外的辅助传感器提供辅助参数,解算运动加速度的值,如文献[9]中是由里程仪测量的速度差获得的,进而通过各轴向测量信息与重力加速度之间的关系获得坡度信息。本文提出了一种新的坡度提取方法,在不需要额外传感器提供辅助参数的情况下,利用重力加速度方向不变性,通过载体坐标系中的重力加速度矢量方向的变化实现道面坡度信息提取。

根据图1所示的坐标系间的关系可知,在坡度测量的过程中,地理坐标系是不动的,导航坐标系只是相对于地理坐标系平移,因此在两个坐标系中的重力加速度向量gn是不变化的。对于载体坐标系,在坡度测量的过程中是存在相对姿态的变化,即载体坐标系相对导航坐标系发生旋转,而且这个角度的变化是与平台所接触面的坡度有关,因此,在载体坐标系中重力加速度向量gb(t)的方向变化量均反映着平台所接触面的坡度变化情况,如图3所示。

图3 坡度提取原理图

假设测量起始时平台由水平面静止状态出发,则起始时刻载体坐标系的重力加速度向量gb(0)为

在时刻t,载体坐标系的重力加速度向量gb(t)为

向量gb(t)与gb(0)间的夹角即为平台在时刻t所处位置的坡度

5 实验结果与分析

实验采用的智能手机为iPhone7,利用其内置的三轴加速度计、三轴陀螺仪和三轴磁力计进行数据采集。手机端MATLAB与电脑端MATLAB通过IP互联的方法,实现传感器采集的数据同步到电脑,从而进行数据处理。此方法需将智能手机与电脑置于同一局域网中,且在智能手机终端安装mobile MATLAB(以下简称mobile),在电脑终端安装MATLAB(R2014a以上版本,以下简称MATLAB),同时需安装插件MATLAB Support Package for IPhone Sensors in MATLAB来匹配手机。该方法实现的过程是首先在MATLAB中与mobile建立连接,然后打开mobile,选择连接电脑,随后输入IP地址、密码和端口默认值,再点击Connect与电脑连接。连接成功后,通过在MATLAB中输入m=mobiledev,可以建立一个采集的对象。通过在命令行中输入m.Logging=1开始进行采样,输入m.Logging=0结束采样。在采样结束后,通过在命令行中输入[a,t]=accellog(m)可以获得整个采集过程中加速度计的采样值,获取其他传感器输出的采样值的过程与此类似。传感器的数据采样率可以通过输入不同的m.SampleRate进行设置,本文实验的数据采样率设置为100 Hz。零加速检测的加速度阈值为thamin=8.0和thamax=10.8,角速度检测阈值为thωmax=1.3。

为检验算法的有效性,第一个实验场地选择在可实测角度与尺寸的楼梯上进行,场景模型如图4所示。此实验的设定是为了模拟含有若干个坡度的道面,因为在实际的道面中很难找到具有这种效果的路线。将智能手机置于小车顶部,手推小车在楼梯上进行下降四层楼梯的运动,将零加速修正的轨迹与未修正的轨迹以及楼梯的真实轨迹进行比较,并将本文方法与常规倾角仪测量的原始方法提取运动过程中的坡度信息进行对比,如图5所示。

图4 楼梯实验场景模型

图5 高度与坡度随位移的变化曲线

由于实验平台呈现刚体效果,在台阶的转折处无法实现理想的90°转折,存在着一定的角度缓变,如图5所示。未修正的轨迹与真实轨迹偏离较大,根据实验数据重建的平台高度变化情况与实际情况具有较好地契合。由图5的坡度变化曲线可见,平台在楼梯平台上水平移动时坡度角为0°,当小车从一个台阶平台边缘下降到另一个台阶平台上的过程中,小车先从水平状态偏转到垂直状态,然后再逐渐从垂直状态恢复为水平状态,坡度从0°减小至-90°,然后再从-90°恢复为0°,具有较好的精度。

第二个实验场地选择在可实测尺寸的斜坡道面上进行,斜坡的坡度值可通过测量斜坡的尺寸值进行计算得到,场景模型如图6所示。此实验场地是在实际道面上,且是一典型的斜坡道面。将智能手机置于小车顶部,手推小车在斜坡道面上进行下降的运动,将零加速修正的轨迹与未修正的轨迹以及斜坡道面的真实轨迹进行比较,并将本文方法与常规倾角仪测量的原始方法提取运动过程中的坡度信息进行对比,如图7所示。

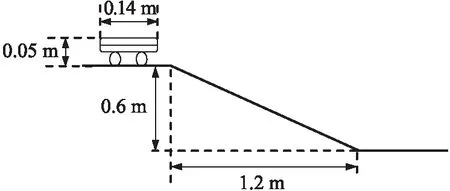
图6 斜坡道面实验场景模型

图7 高度与坡度随位移的变化曲线

由图7的高度变化曲线可见,未修正的轨迹与真实轨迹偏离较大,根据实验数据重建的高度变化情况与实际情况具有较好地契合。由图7的坡度变化曲线可见,实验平台在水平面上移动时坡度角为0°。由于斜面的长度相对于小车的尺寸较大,当小车从水平面运动到斜面的过程中,小车先从水平状态偏转到倾斜状态,在车身完全偏转到斜面之后,可以保持一段时间的倾斜状态,坡度从0°减小至-29°,然后保持一段时间的-29°。当小车从斜面运动到水平面的过程中,小车从倾斜状态偏转到水平状态,坡度从-29°增大至0°。算法得到的坡度值与实际坡度值的误差较小,具有较好的精度。

通过楼梯实验与斜坡道面实验可以得到,将本文方法与原始方法进行对比,两种方法的精度差距很小,但本文方法的优点在于不需要使用额外的辅助传感器解算运动加速度的值,不用区分载体的运动状态,实现了道面坡度的提取。同时,设备的成本较低,可推广的范围更广。

6 结论

本文提出了一种基于智能手机中MEMS传感器的道面坡度提取方法,该方法利用检测出的零加速状态对旋转四元数进行重置,克服了惯性器件进行积分所带来的累积误差问题,并提出了一种新的坡度提取方法,在不需额外传感器提供辅助参数的情况下,基于重力加速度方向不变性,利用载体坐标系中重力加速度向量角度变化实现道面坡度信息提取。实验结果表明该算法可以有效地实现对道面坡度信息的提取和道面坡度位置的定位。