导弹舵机平台磁电编码器的磁场设计与装配误差仿真分析

李 锋,张昆峰

(中国空空导弹研究院,河南 洛阳 471009)

角度传感器是空空导弹舵机系统的重要位置反馈元器件[1],安装在传动机构上[2],对响应速度、精度、可靠性、小体积、长寿命、抗干扰能力有较高的要求[3]。

电位器为接触式传感器[4],存在机械磨损及密封、寿命、可靠性不足等问题,旋转变压器[5]和光电编码器[6]体积较大和其他缺点,难以满足未来空空导弹舵机越来越严酷的使用环境需求。磁电编码器采用磁性元件,基于霍尔效应[7],构成部件少,结构紧凑,易于实现小型化、高精度、高分辨率,具有抗振动、抗冲击特性,以其突出优点在各种传感器中具有明显优势[8]。

磁电编码器的磁场设计决定了其输出精度和性能,进行编码器的磁场设计,确保满足技术要求,并进行装配误差仿真分析,对进一步提高编码器精度具有十分重要的意义。磁电编码器技术要求如下:单磁极,本体直径不大于15 mm,线性度0.3%,数字式分辨率12 bit,重复测量误差≤2 LSB。

1 磁电编码器原理与算法

1.1 磁电编码器原理

磁电编码器通过霍尔阵列检测出旋转磁铁的磁场强度分布,并从磁场变化解析出角位移信息[9],如图1所示。

图1 磁电编码器工作原理框图

磁电编码器磁敏器件布置示意图如图2所示。霍尔器件只对垂直磁场Z敏感,对X、Y磁场均不敏感。当永磁体的转角固定时,四个霍尔器件感应到的电压也为固定值,根据电压的大小计算出永磁体的转角[10]。

图2 磁电编码器磁敏器件布置示意图

1.2 采集算法

永磁体匀速旋转一周四个霍尔器件感应出的正弦波形的电压,相位相差90°[11],如图3所示,将两组对角的电压分别定义为sin_P、sin_N,cos_P、cos_N。

图3 霍尔阵列感应电压示意

设各点Z方向上的磁场强度为Ha、Hb、Hc、Hd。将四路电压合并为两路(该过程可抵消一部分安装误差),得到正弦值与余弦值:

Vs=sin_P-sin_N=Ha-HcVc=cos_P-cos_N=Hb-Hd

根据Vs、Vc的正负与大小,可以将一周360°分为8个区间,每个区间45°,Vs、Vc的反正切值即为霍尔芯片反馈的角度值,计算方法如表1所示。

表1 霍尔芯片感应角度计算方法

2 磁场设计

磁铁材料选用钐钴永磁(Sm2Co17),径向充磁。磁电编码器芯片选用iC-Haus公司的iC-MA3,封装大小为4.0 mm×4.0 mm×0.9 mm,工作电压为5 V,霍尔感应点排列在边长为2 mm的正方形四个角上,磁场强度感应范围为15 kA/m～65 kA/m。在霍尔芯片和磁铁材料选定的情况下,为确定磁电编码器的磁场,需要对磁铁尺寸、磁铁与芯片之间的气隙进行电磁仿真分析与设计。仿真软件为Maxwell 17.2。

考虑磁电编码器轴承尺寸的限制和实际需求,初步选用半径2 mm,厚度分别为4 mm和2 mm的两种磁铁,进行电磁场静态仿真分析和设计。磁场强度监测面为内径1.0 mm、宽度0.1 mm的圆环,用于模拟芯片的磁感应位置。计算得到对应Z方向上的磁场强度,如表2所示。

表2 磁铁尺寸、气隙设计与仿真结果

图4 平面上磁场强度

结合仿真结果,考虑空空导弹舵机平台实际情况和抗磁场干扰需要,并考虑空间尺寸限制和芯片霍尔感应性能,以磁铁厚度2 mm、气隙1.6 mm作为磁电编码器的初步设计方案。

监测霍尔芯片对应平面上磁场强度的分布情况仿真结果如图4所示,平面半径为1.1 mm。可以看出磁场强度最大位置位于圆盘的边缘位置,与霍尔芯片的四个感应点相对应。

磁铁厚度2 mm、气隙1.6 mm时,圆环监测面上Z方向上的磁场强度H如图5所示。

图5 监测面Z方向上磁场强度H

针对该设计方案,进行电磁场动态仿真分析。设磁铁以600 deg/s的速度旋转,观察监测面上磁场强度和向量方向的变化,360°时磁场强度向量如图6 所示,磁场强度Z项分量如图7所示。仿真过程中监测面上磁场强度和向量方向符合要求。

图6 磁场强度向量

图7 磁场强度

通过磁场静态仿真和动态仿真,最终选用磁铁厚度为2 mm、气隙1.6 mm作为磁电编码器的磁场设计方案。

3 结构设计与验证

3.1 结构设计

磁电编码器主要由轴、端盖、轴承、壳体、磁铁、霍尔电路板等部分组成[12],设计总高度20 mm,壳体直径13 mm,壳体厚度0.5 mm,轴凸出壳体10 mm,如图8所示。壳和端盖为铝合金;轴、轴承、磁铁固定套等为不锈钢。

图8 磁电编码器结构示意图

3.2 模型验证

通过对比反馈角度的理论值与仿真值来验证模型的准确性。设定磁以600 deg/s的速度旋转,每 1 ms 理论上磁电编码器的反馈值应为0.6°。在仿真时设定同样的转速,每1ms计算一次反馈角度,仿真曲线如图9所示,仿真值和理论值高度重合。

图9 磁电编码器反馈角度的仿真曲线

3.3 实物装配与验证

装配了1个单磁极磁电编码器,如图10(a)所示。利用成都科奥达DT005P-7200P/RWZ05P光电编码器(7 200线,精度0.05°)对编码器成件进行转动测试,利用上位机采集反馈角度。检测系统如图10(b)所示。

图10 编码器实物及其检测系统

实物测试结果如表3所示,拟合曲线如图11所示,可以得出:编码器的独立线性度为0.27%,旋转360°时的重复测量误差≤2LSB,磁电编码器仿真结果与实测结果满足误差要求。

表3 磁电编码器实物测试结果 (°)

图11 编码器输出结果的拟合

4 装配误差分析

研究磁电编码器装配误差主要表现为磁铁与霍尔芯片的位置误差,主要包含三个方面:①磁铁与霍尔传感器安装位置发生同心偏移;②霍尔传感器安装平面以bd线为中心发生对角偏转;③霍尔传感器安装平面以ab线与cd线之间的中轴线为中心发生对称偏转。

设定磁铁以600 deg/s的速度旋转,计算步长,每1 ms存储一次数据,磁铁旋转360°,进行磁电编码器的装配误差分析。

4.1 同心偏移

假设磁铁安装位置中心沿着X轴负向分别偏移了0.2 mm、0.5 mm、0.7 mm、1.0mm,如图12所示。反馈结果仿真曲线如图13所示.截取0～90°之间的仿真曲线的局部放大图,如图14所示。

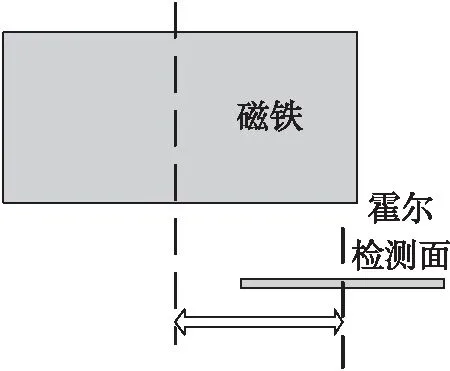
图12 同心偏移示意图

图13 同心偏移仿真曲线

图14 同心偏移角度局部放大图

从图13、图14可以看出:①同心偏移越大,磁电编码器输出值的误差越大,且输出值交替变化;②发生同心偏移的情况下,在45°、135°、225°、315°位置时,磁电编码器的输出值误差最大;③同心偏移0.2 mm以内,磁电编码器的输出值误差最大不超过0.8°;偏移0.5 mm时误差最大为1.8°;偏移0.7 mm时误差最大为2.5°,偏移1.0 mm时误差最大为12.7°。可得出:同心偏移0.2 mm以内不影响磁电编码器的使用;同心偏移超过0.5 mm后,磁电编码器输出值不准确。

4.2 对角偏转

假设在装配过程中,霍尔传感器安装位置以bd线为中心分别偏转了2°、5°、10°、15°,霍尔感应点由a、c分别偏转到a′、c′位置,如图15所示。反馈结果仿真曲线如图16所示。截取0～90°之间的仿真曲线的局部放大图,如图17所示。

图15 对角偏转示意图

图16 对角偏转仿真曲线

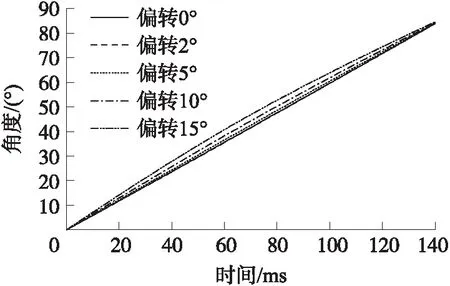
图17 对角偏转角度局部放大图

从图16、图17可以看出:①对角偏转角度越大,输出值误差越大;且输出值交替变化;②发生对角偏转后,在45°、135°、225°、315°位置时,磁电编码器的输出值误差最大;③对角偏转2°以内,输出值误差最大不超过0.2°;偏转5°时误差最大为0.98°;偏转10°时误差最大为2.7°,偏转15°时误差最大为5.7°。可得出:对角偏转5°以内不影响磁电编码器的使用;同心偏移超过5°后,磁电编码器输出值不准确。

图18 对称偏转示意图

4.3 对称偏转

假设霍尔传感器安装平面以ab线与cd线之间的中轴线为中心发生了对称偏转,分别偏转了2°、5°、7°、10°,如图18所示。仿真曲线如图19所示。

图19 对称偏转仿真曲线

从图19可以看出:在装配过程中,霍尔传感器发生一定范围内的对称偏转情况下,磁电编码器输出值误差较小,这是由反正切的采集计算方法决定的。

5 结论

通过对磁电编码器进行磁场设计和仿真分析,设计了一款小型高精度磁电编码器,满足线性度0.3%、分辨率12 bit、重复测量误差≤2 LSB的使用要求。

通过对磁电编码器的装配误差进行磁场仿真分析,研究了存在同心偏移、对角偏转、对称偏转等形式装配误差情况下磁电编码器的输出特性:同心偏移或者对角偏转时,安装位置在同心偏移0.2 mm以内,对角偏转5°以内,磁电编码器的输出误差在允许范围内;霍尔传感器安装平面以中轴线为中心发生对称偏转对磁电编码器的输出值误差影响较小。

在装配过程中,要尽量避免发生同心偏移或对角偏转,保证磁铁平面与霍尔传感器安装平面保持平行,特别是严格要求磁铁与霍尔传感器同心度的装配工艺。另外,一旦出现装配误差,可根据计算结果进行相应的软件或硬件补偿,提高成品率。