对高考真题中分段函数考查的分类解析

王海平

(广东省惠阳高级中学实验学校 516057)

在高中数学考试大纲中，对分段函数的知识点有如下要求:(1)了解构成函数的要素，会求一些简单函数的定义域和值域；了解映射的概念. (2)在实际情境中，会根据不同的需要选择恰当的方法表示函数.(3)了解简单的分段函数，并能简单应用. (4)理解函数的单调性、最大值、最小值及其几何意义；结合具体函数，了解函数奇偶性的含义.(5)会运用函数图象理解和研究函数的性质.对近年来的高考试卷分析后，重点有以下三个考点，

一、求简单的分段函数的函数值

分段函数的求解过程,常要结合分段讨论和数形结合的思想,解题完成后再进行代入检验.

A．3 B．6 C．9 D．12

答案:C

解析由已知得f(-2)=1+log24=3.又log212>1，所以f(log212)=2log212-1=2log26=6.故f(-2)+f(log212)=9，故选C．

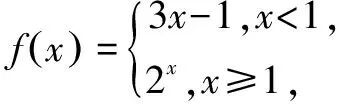
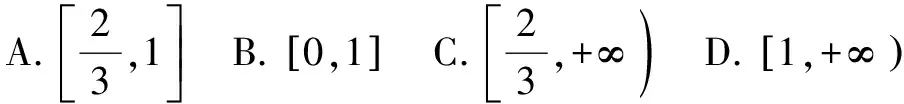
答案：C

解析当a≥1时,f(a)=2a>1,所以,f(f(a))=2f(a),即a>1符合题意.

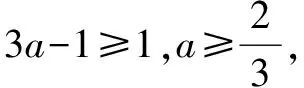
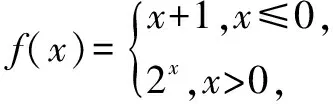
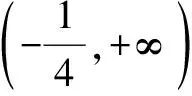
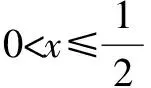
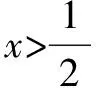
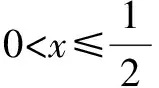
二、求分段函数的单调性

函数的单调性是关于函数的一个重点考查角度,由于对分段函数的单调性的考查题目设置角度丰富,涵盖的知识点具有多样性和灵活性,因此相关的题目也丰富多彩.

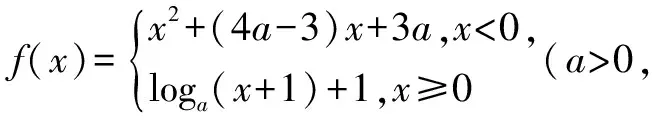
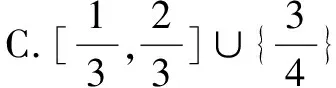
答案：C.

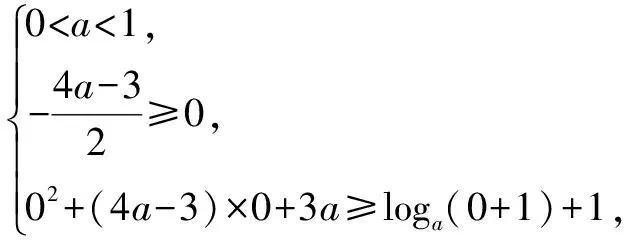
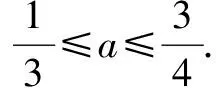
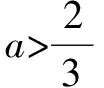
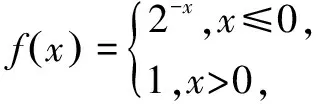
A．(-∞，1] B．(0，+∞)

C．(-1，0) D．(-∞，0)

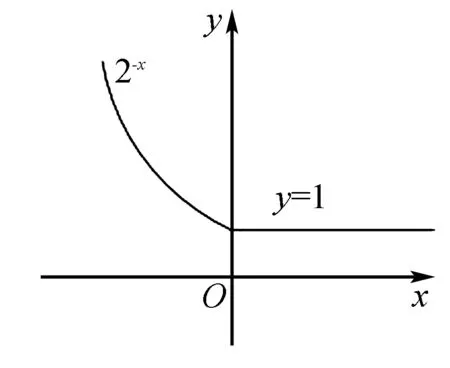
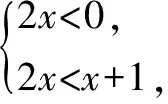
点评例题一给出了分段函数的单调性,要求符合题意的参数范围,例题二给出了两个函数值的大小,要求得出自变量的范围,这类型题目都是在考查给定函数的变化情况,也就是函数的单调性,研究分段函数的单调性,首先需要确定在不同范围上各个初等函数的变化情况,然后再结合分段函数的单调性判断各段函数的临界点需要满足的约束条件,需要同学们对基本初等函数的研究到位并且具有从局部到整体的解决问题的角度.

三、求分段函数的值域

对分段函数的值域的考查可以看作是对分段函数单调性的考查的一个延伸,是在对分段函数的变化情况的研究后对函数值的范围的判断,常常也需要对分段函数的图象有基本的把握.

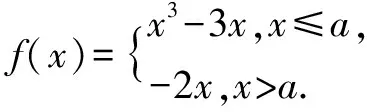
①若a=0，则f(x)的最大值为____；

②若f(x)无最大值，则实数a的取值范围是____.

答案：2,(-∞,-1).

解析求分段函数的最值时，应从局部到整体,根据自变量的范围选择相应的解析式,先确定每个解析式在相应范围上的最值,再整体比较得出分段函数的最值.含有参数的问题,还需要有对图象进行变化的能力.

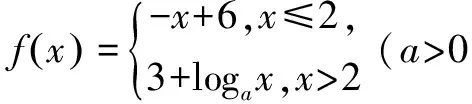
答案：(1,2]

解析当x≤2，故-x+6≥4，要使得函数f(x)的值域为[4,+∞)，只需f1(x)=3+logax(x>2)的值域包含于[4,+∞)，故a>1，所以f1(x)>3+loga2，所以3+loga2≥4，解得1

点评例题2考查分段函数的值域问题，是一个需要逆向思维的问题,分段函数的问题需要分段讨论,其中每个范围中得到的解集必须是相应范围的子集,最终答案应该是各个范围下解的集合的并集,此类题目题型传统,解答方法单一,属于中档题目.