无患子复叶气动特性研究

赵洪涛,邵传平

(中国计量大学 计量测试工程学院,浙江 杭州 310018)

树木作为自然界最常见的植被之一经过数万年的进化拥有极其庞大的种群,人类对树木的研究不仅仅局限在植物学和园林学等,树木在仿生学及空气动力学方面的研究中也处于重要的地位。张昊明[1]通过银杏叶片的形状制作了仿生天线。Sharif等[2]利用树叶在风中振动原理制作的一种太阳能发电板,相比普通发电板具有更好的适应风力较大的情况。陈志超等[3]基于树叶仿生学设计了大展弦比机翼,通过有限元验证仿生机翼符合设计要求。

Vogel[4]对单片树叶及复叶进行实验发现随着风速增加叶片逐渐形成锥状。邵传平等[5]研究构树叶叶片角在风速小于6 m/s时快速减小。Albayrak等[6]研究发现形状是影响树叶与流体之间相互作用的重要因素。Shao等[7]对鹅掌楸通过在风洞中研究发现鹅掌楸重构变形主要为飞翼状及锥状。

Milne[8]研究发现树木风振与风载荷及树木固有频率相关。Shao等[9]发现树叶振动可由叶柄振动引起,也可由叶片及叶梢上下拍动引起。Vogel[10]对白杨树叶在风洞中实验发现在风速0～30 m/s范围内白杨树叶持续振动且不受到破坏。邵传平和朱园园[11]研究发现阔叶树叶在特定风速下存在振动频率不同的现象且振动频率先增后减。

1 实验材料和方法

实验所用无患子复叶均采摘自6月中上旬中国计量大学校区内,且采摘的无患子复叶必须完整无残缺及黄斑。采摘的无患子复叶放在清水中保鲜,并在2小时内全部用于实验,每次实验前重新采摘新鲜无患子复叶。

实验全部在中国计量大学循环风洞内进行,风洞可以产生0～22.7 m/s湍流小于0.5%的风场。风洞实验段长2 m,宽、高各0.6 m,在顶端开有通孔用来固定实验所用无患子复叶的连接杆连接至位于风洞实验段上壁的六分量测量天平上,可以实时测量x、y、z三方向力及力矩,实验所用采样频率为50 kHz,采集时间为15.6 s,图1为复叶在风洞在迎风示意图。实验用位于侧面及底面的高速摄像机拍摄记录无患子复叶形态变化,随着风速的增加要调整相机位置使拍出来的复叶图像始终位于图片中心位置。

图1 复叶在风洞中悬挂方式Figure 1 Sketch of the Compound Leaves in wind tunnel

无患子复叶由叶片及枝条组成,叶片左右对称分布无尾叶,相比单片树叶,其气动特性受叶片之间集群效应影响更为复杂,但整棵树多枝叶多复叶粗枝干相比气动特性较为简单,且无患子分布广泛易获得,是一种理想型研究材料。

2 实验结果及分析

2.1 无患子复叶形态分析

对无患子正面迎风进行实验,无患子复叶出现六种状态分别为叶轴大幅弯曲、U型稳定、叶轴低频振动、叶片对合稳定、高频振动及合成卷稳定。图2为有个10叶片的无患子复叶正面迎风的情况,对于其他叶片数的复叶具有相同的规律。

如图2(a),0.7 m/s风速下复叶呈自然下垂状态悬挂在风洞中,其中枝条有一定的弯曲,叶片呈现自然伸展状态。

如图2(b),当风速达到1.9 m/s时,叶轴弯曲明显增大,叶轴由自然下垂状态变为叶轴大幅弯曲状态,但复叶整体仍处于静止状态,并且叶片由自然伸展状态向内靠拢,每对叶片间距逐渐减小,但此时复叶整体仍呈稳定状态。我们将此种状态称为叶轴大幅弯曲状态。

如图2(c),风速达到4.8 m/s时,复叶叶片依次向内合拢,复叶呈现U型状态,类似于两个手掌向上捧举。

如图2(d1)和2(d2),当风速达到9.0 m/s时,复叶低振频、低振幅上下振动,此时最上方一对叶片开始上下振动,其他部分叶片相互对合没有发生振动,当枝条开始振动时,往往伴随着叶片振动。

如图2(e),当风速为10.4 m/s时,所有叶片向内合拢,每对叶片相对紧贴在一起,类似于两个手掌对合。复叶呈现叶片对合稳定状态,复叶再次达到平衡。此时状态称为叶片对合稳定状态。

图2 复叶正面迎风时随风速的变化Figure 2 Front surface facing the wind status changes with wind speed

如图2(f1)与2(f2),当风速达到13.2 m/s时,复叶高频无规律振动,同时伴随着叶片无规律振动。

如图2(g),当风速达到17.2 m/s时每对叶片停止振动沿着叶轴方向依次向内对合,上层叶片堆叠在下层叶片之上,复叶呈合成卷稳定状态。

对无患子复叶反面进行迎风实验,反面迎风出现正面迎风相同的6种状态,但反面迎风比正面相比出现振动更少,说明复叶反面迎风比正面迎风更容易处于稳定状态,正面迎风不易保持自身稳定。

表1 复叶正反面迎风各状态出现概率

Table 1 Probability of front and back compound leaves status %

2.2 复叶弯曲角度分析

为了更好地研究复叶变形情况,如图1所示我们取代表叶轴弯曲程度的叶轴倾角θ及叶片叶脉与z轴之间的夹角平均值叶片角θ1作为特征角。

如图3(a)和3(b)分别为某个复叶叶轴倾角θ和叶片角θ1随风速变化典型情况。当风速为0时,在x-z平面叶轴自然向下θ=7°,叶片大约有-15°的倾角。

图3 复叶特征角随风速变化曲线Figure 3 Characteristic angle changed with wind speed

在风速0～7.7 m/s范围内,叶轴倾角由5°快速线性增加到79°左右,风速在9.0～11.8 m/s范围内时,由于叶片发生重构致使叶轴倾角发生8°左右的减小。

在风速为13.2 m/s时叶轴发生振动,叶轴倾角出现±5°变化,在风速在14.5～20 m/s范围内叶轴出现连续振动,叶轴倾角出现±10°左右的变化,随着风速的继续增加,叶轴倾角最终稳定在85°左右。

在风速0～7.7 m/s范围内叶片倾角由-15°快速增加至100°左右,在风速为9.0 m/s时由于叶片发生重构,叶片倾角出现小幅下降,在风速10.4～15.9 m/s范围内,叶片发生连续振动,叶片倾角出现±15°左右的大幅变化在风速为17.2 m/s时叶片再次发生振动,叶片倾角出现±10°左右的变化。

为了更好体现相似关系,现引入雷诺数Re,其定义如下:

式(1)中,ρ为空气密度,V为实时风速,L为复叶长度,μ为空气粘滞系数。如图4,为35串无患子复叶叶轴倾角θ随雷诺数变化趋势,随着雷诺数增加叶轴倾角θ呈现开口向下抛物线增长模式,且最终叶轴倾角θ稳定在80°附近;随着雷诺数增加,复叶逐渐呈流线体以保持自身稳定,当复叶整体与来方向一致时所受阻力最小。

图4 叶轴倾角θ与雷诺数Re变化关系Figure 4 Rachis inclination θ changed with Re

2.3 复叶宽度随风速变化分析

图5为无患子复叶横向宽度示意图,其宽度随风速不断变化,为了体现宽度变化程度引进相对变化数b=Bv/B,其中Bv是在某风速下复叶串横向宽度,B为复叶串自然状态下宽度。

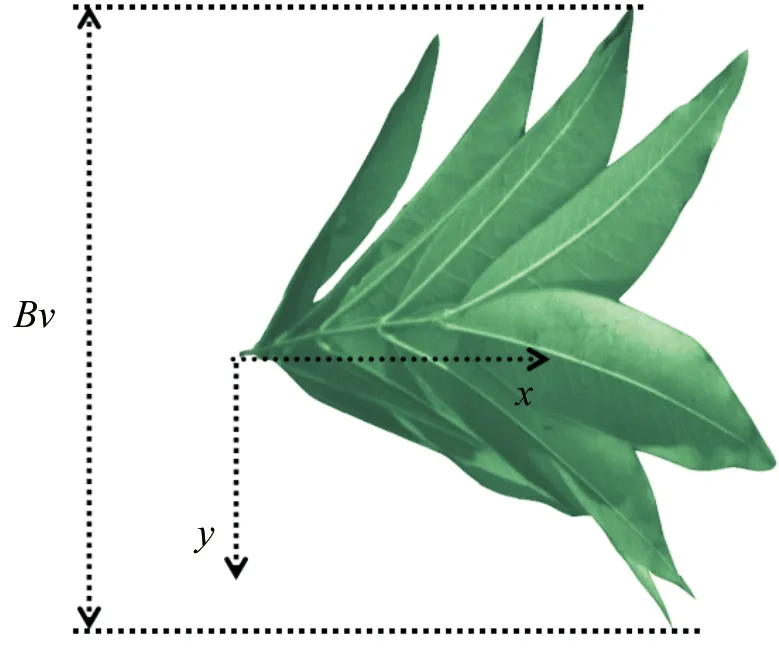
图5 复叶宽度Figure 5 Compound leaves width

实验统计了45串无患子复叶正面迎风特征宽度平均值随风速变化关系。如图6,在风速0.7～1.9 m/s范围内特征宽度保持不变,在风速为3.5 m/s时风将原有弯曲的叶片吹舒展开特征宽度相对变化数大于1,在风速4.8～10.4 m/s内成线性递减函数,在风速9 m/s时特征宽度相对变化数减小了50%,在风速为18.6 m/s时特征宽度出现轻微增长,最终特征宽度相对变化数稳定在0.2附近。

图6 复叶特征宽度随风速变化Figure 6 Feature width changed with wind

2.4 叶轴末端位移统计分析

无患子复叶在风洞中受力弯曲,枝条末端会在空间内发生位移,现将位移s沿受力方向分解为x方向位移、y方向位移与z方向位移,由于不同无患子复叶枝条长度不同,为了更好的研究相似关系,现引入无量纲参数:

(2)

(3)

(4)

式(2)～(4)中,l为复叶叶轴长度。

如图7为无患子复叶枝条末端沿x方向位移与z方向位移随雷诺数Re变化示意图,随着雷诺数的增大x方向位移呈开口向下抛物线形式,z方向位移呈线性增加趋势。

图7 x、z方向位移随雷诺数Re变化Figure 7 x,z displacement changed with Re

如图8为10个复叶在x-z平面内,x′、z′随雷诺数Re变化趋势图。在雷诺数为0～2.1×105范围内z′随x′变化趋势呈开口向上抛物线形式。

图8 叶轴末端位移在x-z平面内变化Figure 8 Rachis tail displacement in the x-z plane

图9为某复叶叶轴末端在空间中移动轨迹图。可知,其移动在空间中为螺旋式上升。

图9 叶轴末端位移在空间变化Figure 9 Rachis tail displacement in the space

3 结 论

在0～22.7 m/s实验风速范围内,无患子复叶出现稳定振动交替出现的形式,随着风速的增加,无患子复叶出现四种稳定状态及两种振动状态,对于振动状态低频振动状态出现的概率小于高频振动的概率。其中反面迎风出现振动的概率要小于正面迎风出现振动的概率,说明反面迎风无患子复叶具有更好的稳定性。随着风速增大复叶宽度相对变化数逐渐减小,最终复叶特征宽度相对变化数稳定在0.2附近。

由于复叶及叶片发生振动导致叶轴倾角与叶片倾角在一定范围内波动,叶轴倾角最终稳定在80°附近,叶片倾角最终稳定在90°附近。随着雷诺数增加x方向位移呈开口向下抛物线形式,z方向位移呈线性增加,叶轴末端位移在x-z平面内,呈开口向上抛物线形式,叶轴末端位移在空间范围内呈现螺旋式上升趋势。