一种拉普拉斯金字塔结构的团网络超分辨率图像重建算法

贾婷婷，王济浩，郑雅羽，冯 杰2(浙江工业大学信息工程学院，杭州30023)

2(浙江理工大学信息学院，杭州310018)

E-mail:yayuzheng@zjut.edu.cn

1 引言

超分辨率图像重建(Super resolution image reconstruction，SRIR或SR)是指用信号处理和图像处理的方法，通过软件算法的方式将已有的低分辨率(Low-resolution，LR)图像转换成高分辨率(High-resolution，HR)图像的技术［1］.SR 适用于解决各种计算机视觉方面的任务，如遥感卫星、安全与监视成像、医学成像、图像生成等.常用的SR方法有基于插值的算法、基于重建的算法和基于学习的算法.基于插值的算法根据图像先验信息和统计模型进行插值计算，实现简单、计算复杂度低，但是重建结果在边缘处存在环或锯齿效应，得到的结果比较模糊［2］.基于重建的算法从同一场景下的多帧LR图像中提取高频信息，融合生成HR图像，但是需要在合适的先验假设下才能获得较好的重建效果.基于学习的算法主要是对高低分辨率训练样本的学习，构造高低分辨率字典对.与基于插值和基于重建的方法相比，基于学习的算法可以获得更多的高频信息，从而得到更加清晰的纹理细节，获取更好的重建效果，因此得到更多关注.

在基于学习的SR重建算法中，Yang等［3］提出的基于稀疏表示的超分辨率图像重建算法表现最为突出，通过高分辨率图像样本训练出具有相同稀疏表示的高低分辨率字典对，从而重建出较好的高分辨率图像.但是，该算法容易出现块效应.黄等［4］引入自回归正则化和非局部相似正则化，对稀疏表示系数的求解进行约束，并对重建后的高分辨率图像进行全局优化.该算法对基于稀疏表示的超分辨率图像重建方法进行了优化，提高了算法的鲁棒性与重建图像的质量.虽然上述方法重建后的图像优于基于插值与基于重建的方法，但是对通用图像的超分辨率重建效果却不甚理想.

近年来，随着计算机硬件计算力的大幅提升，卷积神经网络在计算机视觉任务中取得了一系列巨大的成功.因此，越来越多的基于深度学习(deep learning，DL)的模型，尤其是卷积神经网络(convolutional neural network，CNN)，被广泛用于SR领域.

Dong等［5］首先提出了SRCNN算法，学习非线性LR到HR映射，将一个三层卷积神经网络引入到超分辨率网络中.Kim等通过裁剪梯度，跳跃连接或递归学习的方式增加VDSR［6］和DRCN［7］算法中的网络深度，以减轻网络深度增加带来的训练问题.上述方法虽然优于传统的基于学习的方法，更加适用通用图像的超分辨率重建.但是，在预测之前，直接使用预定义的上采样算子将输入图像升高到期望输出的空间分辨率.这将会增加不必要的计算成本，并且会经常导致可见的重建伪像.

为了减少不必要的计算成本，削弱可见的伪像，Dong等［8］提出了FSRCNN算法.不再使用预定义的上采样算子，直接将原始低分辨率图像作为输入并在最后一步引入转置卷积进行上采样.Lai等［9］提出了一种级联结构的超分辨率算法LapSRN，能够在多个分辨率下生成中间SR预测，并逐步进行优化，取得了较好的重建效果.但是这些方法均采用链式的方式堆叠构建模块，仅重视卷积层之间的前向信息传递，从而忽视了卷积层之间的反馈交流信息.

因此，本文提出了一种拉普拉斯金字塔结构的团网络超分辨率图像重建算法(A Clique Network Super-resolution Image Reconstruction Algorithm Based on Laplace Pyramid Structure，LCN).为了最大化卷积层间的交流，提取更多的特征.本文将团网CliqueNet［10］中的团块 Clique Block引入 SR 网络，并对CliqueNet做进一步的改善，将改进后的结构命名为CNB，作为LCN的构建模块.同一个CNB中的任意两个卷积层之间都有前向和反馈连接，层间信息交替更新，以便信息流和反馈机制可以最大化，层间的连接更加密集.同时采用拉普拉斯金字塔结构，通过渐进式重建高分辨率图像的方式，逐步地优化重建结果.并将残差学习应用到网络中，减少网络参数，避免梯度爆炸.从实验结果看，本文提出的算法在主观与客观都产生了较好的重建效果，尤其是在对边缘与线条的重建上.

2 拉普拉斯金字塔结构的团网络

2.1 网络结构

本文提出了一种拉普拉斯金字塔结构的团网络.拉普拉斯金字塔结构已经广泛应用于图像混叠、纹理合成、边缘感知过滤和语义分割等［11］领域，并取得较好的结果.因此，本文网络采用拉普拉斯金字塔结构，能够通过渐进式重建高分辨率图像的方式，逐步优化重建的结果.

同时将改进后的团网CNB作为拉普拉斯金字塔结构的构建模块.目前，团网CilqueNet仅被用于高级计算机视觉任务(例如，对象识别等).该网络可以最大化卷积层间的交流，提取更多的特征.因此，本文对其进行改进，并引入SR网络中.

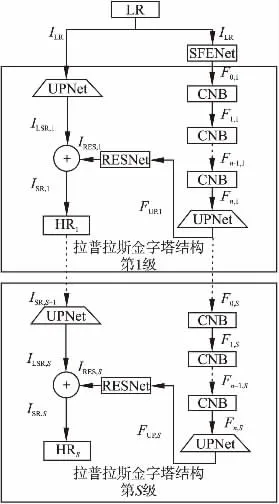
图1 LCN结构Fig.1 LCN structure

网络结构如图1所示，将ILR作为系统的输入，ISR，S作为拉普拉斯金字塔结构第S级重建网络的输出.则ISR，S可由下式得出:

其中，HLCN，S()表示获得拉普拉斯金字塔第S级高分辨率图像HR的过程，可以是复合函数.关于LCN的更多细节将在2.2与2.3节中详细给出.

2.2 拉普拉斯金字塔结构

本文网络采用拉普拉斯金字塔结构.如图1所示，在金字塔结构的每个层级中均包含特征提取和图像重建两个过程.

由于低分辨率图像与高分辨率图像在信息上有很多地方是共享的，因此本文仅对残差进行学习.在特征提取过程中获取残差图像，在图像重建过程中将残差图像与低分辨率图像矩阵相加，获得高分辨率图像.从而减少网络参数，有利于梯度传输，防止梯度消失或梯度爆炸.

2.2.1 特征提取

对于一个非常深的网络来说，直接将LR空间中的每个卷积层所提取到的全部特征都输出是困难和不切实际的.因此，本文提出使用CNB作为拉普拉斯金字塔结构的构建模块，以便可以提取更多的特征.

在拉普拉斯金字塔的每个层级中，特征提取均由CNB构建模块、上采样网络(UPNet)、残差提取网络(RESNet)三个部分组成.输入依次经过CNB构建模块、上采样网络、残差提取网络，预测在当前金字塔层级上的残差图像.其中，每个上采样网的输出连接到两个不同的层，其中一层用于在金字塔本层级上提取残差图像，另一层作为金字塔下一层级特征提取的输入.

将F0，S作为拉普拉斯金字塔S级的输入，假设在拉普拉斯金字塔结构的第S级中有n个CNB构建模块，则第n个CNB构建模块的输出Fn，S可由下式得出:

其中，HCNB，n()表示第n个CNB构建模块的特征提取，可以是复合函数.关于CNB构建模块的更多细节将在2.3节中给出.HSFE()表示网络输入ILR经过浅层特征提取网络(SFENet)，进行特征提取的卷积运算.

在获得CNB构建模块提取到的细节特征之后，使用上采样网络对其进行上采样，则图像在S级上获得的上采样特征FUP，S可由下式所得:

其中，HUP()表示卷积运算.输入Fn，S为S级中经过n个CNB构建模块后所获得的细节特征.

在获得上采样特征之后，使用残差提取网络来获取残差图像，则在拉普拉斯金字塔S级中生成的残差图像IRES，S可由下式得出:

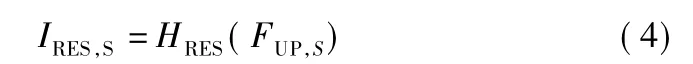
其中，HRES()表示卷积运算.输入为金字塔S级图像经过上采样网络后得到的特征FUP，S.至此，拉普拉斯金字塔结构第S级的特征提取完成.

2.2.2 图像重建

在拉普拉斯金字塔的每个层级中，图像重建主要由上采样网(UPNet)和残差融合两部分组成.输入首先经过上采样网，然后将上采样得到的放大后的低分辨率图像与来自特征提取分支获得的残差图像进行像素求和，以产生高分辨率的输出图像.同时将输出的高分辨率图像作为下一级金字塔的输入，重建下一级的高分辨率图像.

在金字塔S(S＞=1)级上，当S=1时，使用上采样网对输入的低分辨率图片进行上采样.除此之外，使用上采样网对S－1级生成的高分辨率图像进行上采样.上采样后获得的放大的低分辨率图像可由下式得出:

其中，HUP()表示卷积运算.输入ILR为低分辨率图片，ISR，S－1为 S －1 级重建网络的输出.

最后将上采样获得的低分辨图像ILSR，S与特征提取获得的残差IRES，S进行融合，获得金字塔S级重建的高分辨率图像ISR，S可由下式得出:

至此，拉普拉斯金字塔结构的超分辨率图像重建完成.

2.3 CNB 构建模块

如图2所示为具有4层结构的Clique Block模块.除了输入节点F0，n，S外，同一Clique Block中的任意两层之间都是双向连接的，即任意层都是另一层的输入和输出.每一个Clique Block有两个阶段组成，第一个阶段用于初始化团块中的所有层，从第二阶段开始，这些层将会被重复提取.

由于本文是专为图像SR设计的网络.因此，我们将CilqueNet进行改进.首先，我们删除了与卷积层消耗相同数量GPU内存的批量标准化(Batch Normalization，BN)层，该层增加了计算复杂度，并且降低了网络的泛化性能.其次，由于池化层的存在，将导致网络丢弃一些像素级别的信息，因此我们删除了池化层.最后，我们通过使用局部特征融合(LFFNet)网络，将网络中第二阶段循环k次提取的到全部特征进行融合，以充分的利用分层特征，这在CilqueNet网络中是被忽略的.我们将改进后的结构称为CNB构建模块.

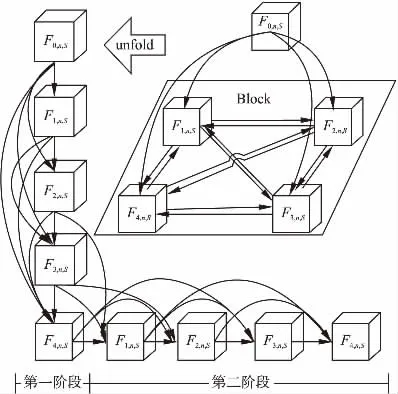
图2 Clique Block 结构［10］Fig.2 Clique Block structure［10］

本文提出的具有5层的CNB构建模块如图3所示.包含团连通网络与局部特征融合(LFFNet)网络.在团连通网络中，除了输入节点外，同一CNB中的任意两层之间都是双向连接，层间交替更新的.第一阶段，用于初始化块中的所有层.第二阶段，这些层将会被重复提取，重复更新.由于第二个阶段提取了更多的特征，因此，在局部特征融合网络中，我们将团连通网络中，第二阶段循环k次提取到的特征进行融合，作为下一个CNB构建模块的输入.

图3 CNB结构Fig.3 CNB structure

2.3.1 团连通网络

第一阶段，输入层Fn－1，S通过单向连接初始化该CNB构建模块中的其他所有层，每个更新的层被连接起来以更新下一层.我们将进行更新的层设为顶层，其他各层设为底层，且将底层的相应参数连接.为了方便后面通用式子的推导，我们将输入节点 Fn－1，S改写为 F10，n，S.则第一阶段，金字塔 S 级中的第n个CNB中的输入节点如下所示:

因此，第一阶段，金字塔S层级中，第n个CNB构建模块的第c层输出可由此通用式得出:

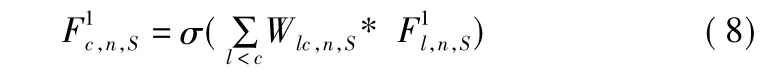
其中，σ()表示非线性激活函数，*表示带参数W的卷积运算.Wij，n，S表示更新过程中各层之间的权值，Wij，n，S在不同阶段重复使用，每一层都将从最近更新的层接收反馈信息.

第二阶段开始，各层开始交替更新.我们同样将进行更新的层设为顶层，其他各层设为底层，且将底层的相应参数连接.因此，金字塔 S层级中，第 n个 CNB构建模块的第c(c＞=1)层，在第二阶段，第k次(k＞=2)循环中的输出可由此通用式得出:

具有5层CNB的传递如表1所示.由两个阶段组成，第一个阶段用于初始化块中的所有层，第二个阶段开始，这些层将会被重复提取，进行k次交替更新.

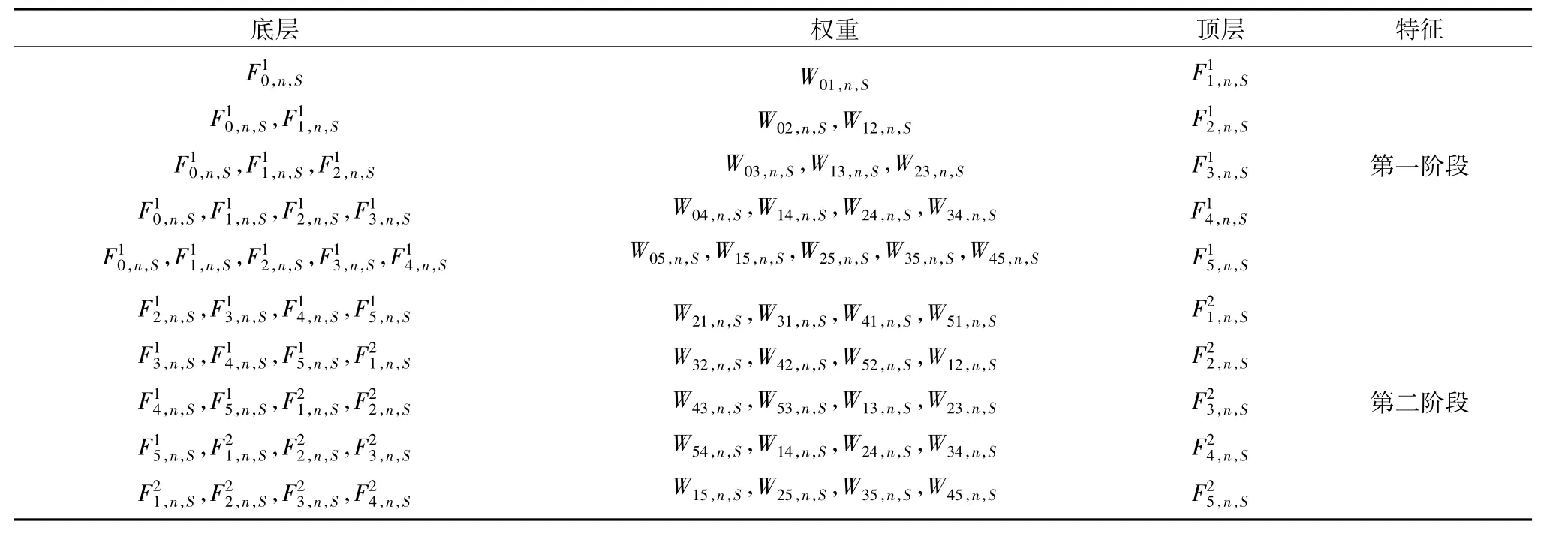
表1 层数为5的团块信息传递［10］Table 1 Clique block information transfer with layer number 5［10］

2.3.2 局部特征融合网络

由于第二个阶段提取了更多的特征，因此应用局部特征融合(LFFNet)网络，自适应的融合第二阶段第k(k＞=2)次循环提取到的局部特征.本文使用卷积层内核大小为1×1，自适应地控制输出信息，则融合后的第n个CNB构建模块的输出为Fn，S可由下式得出:

其中，HLFF()表示卷积运算.至此，CNB构建模块特征提取完成.

3 实验结果与分析

首先，对本文的实验设置进行描述.然后，对网络结构的有效性进行分析.接着，与其他算法在4个基准数据集上进行测试，并将所测的平均值与其他算法进行对比，为了对比的公正性，本文算法与另外6种算法均使用相同的训练集.最后，将展示本文算法在解决通用图像方面的有效性.

3.1 实验设置

硬件平台配置.本文硬件实验平台的处理器为Intel(R)Core(TM)i7-7700，主频为 3.6GHz，内存为 16GB.

训练集与测试集.本文使用了291张图片作为训练数据集，其中91张图片来自Yang［12］等人，其他的200张图片来自Berkeley Segmentation Dataset［13］训 练 集.VDSR、DRCN、LapSRN也使用相同的训练数据集，后面我们将会与这些模型进行对比.我们使用4个被广泛使用的基准数据集Set5、Set14、BSDS100和 Urban100进行测试.其中，Set5、Set14和BSDS100由自然场景组成，Urban100由具有不同细节的具有挑战的城市场景图像组成.

训练设置.将RGB图像转换为YCbCr信号，本文只对亮度通道Y进行超分辨重建，Cb、Cr通道进行双三次插值放大.因此，输入图像与输出图像具有相同的大小.以三种方式增加训练数据:1)缩放:按照［1，0.9，0.8，0.7，0.6，0.5］倍数进行图像的缩小;2)旋转:将图像旋转90度、180度以及270度;3)翻转:以0.5的概率水平和垂直翻转图像.将动量参数设置为0.9，权值衰减设置为1e-4，学习率设置为1e-4.

训练细节.输入的LR图像通过内核大小为3×3的卷积，输出通道设置为64，作为金字塔第1层级特征提取分支的输入.卷积之前在输入的边界填充零，以保持输出的大小与每个金字塔层级的输入相同.转置卷积的卷积层内核大小为4×4.每个CNB中，团连通网络的卷积层内核大小均为3×3，局部特征融合网络的卷积层内核大小为1×1.除这些之外，其余卷积核的大小均为3×3.

测试设置.使用变换后的YCbCr空间的Y分量上的峰值信噪比PSNR和结构相似性SSIM［14］评估HR图像，最优值用粗体标出.

3.2 模型分析

拉普拉斯金字塔结构.为了说明金字塔模型的有效性，我们删除网络的金字塔结构进行4倍放大因子的训练并测试，与本文的LCN算法进行对比.为了对比的有效性，除了金字塔结构使用与否外，两个网络使用相同的训练数据集，输入均采用双三次下采样的LR图片，并通过相同个数的CNB构建模块.最后我们在两个基准数据集Set5和BSDS100上进行测试，测试结果如表2所示.由表2可知，在Set5与BSDS100这两个测试数据集上，拉普拉斯金字塔结构在客观评价指标PSNR/SSIM上对重建的 HR图像分别有0.19dB/0.003和0.09dB/0.001的提升.其中，文中所述结果均为在相应数据集上的平均值.

表2 金字塔结构对网络的影响Table 2 Impact of pyramid structure on the network

CNB构建模块个数.我们将CNB构建模块的个数n分别设置为1、2和3，同时进行4倍放大因子的训练与测试.为了测试的公正性，除了CNB构建模块的个数不同以外，其他各项均保持一致.将每个CNB构建模块中的层数c设置为5.在两个基准数据集上测试，得到CNB构建模块的数量对网络的影响.由表3可知，在Set5与BSDS100这两个测试数据集上，当CNB构建模块的个数n由1增加到2时，图像的评价指标PSNR/SSIM随着网络复杂度的提升而有0.11dB/0.007和0.02dB/0.001 的提升.但是，当网络的复杂度到达一定程度时，网络参数增加，仅通过残差学习来减少网络参数已经无法满足网络.因此，CNB构建模块的个数由2增加到3后，网络的性能非但没有增加，反而稍有下降，如表3所示.

CNB构建模块层数.我们将CNB构建模块的层数c分别设置为3、4、5并进行4倍放大因子的训练与测试.将每个CNB的个数n设置为2，得到CNB构建模块中层数c对网络的影响.由表4可知，随着层数c由3增加到4，在Set5和BSDS100这两个测试数据集上，图像的评价指标PSNR/SSIM有 0.10dB/0.001和0.01dB/0.001的提升.但是当c由4增加到5后，在测试数据集Set5中，图像的评价指标PSNR/SSIM 依然有0.06dB/0.001的提升，在测试数据集BSDS100

表3 CNB个数n对网络的影响Table 3 Impact of the number of CNBs on the network

表4 CNB层数c对网络的影响Table 4 Impact of CNB layer number c on the network

中，网络的性能评价指标SSIM却稍有下降.综合考虑，本文选择n为2，c为5作为模型的最佳参数与其他算法进行对比.

3.3 算法对比

表5 算法定量对比Table 5 Quantitative comparison between algorithms

由于训练数据集将会对算法的测试产生影响.为了对比的公正性，我们的LCN与下面6种基于学习的超分辨率算法SRCNN、FSRCNN、VDSR、DRCN、LapSRN、RSRD［15］均使用相同的291张数据集进行训练.表5显示了上述算法与本文提出的LCN算法在4个基准测试数据集上，放大因子为2以及4的定量对比.其中，表内其他算法在相应数据集上测试的结果引用LapSRN与RSRD论文中公开发表的数据.

由表5可知，在使用相同训练数据集的情况下，本文算法优于上述算法.在客观指标上，本文提出的算法重建后的图像在客观评价指标PSNR与SSIM上分别有0.05dB至0.36dB与0.001至0.006的提升.在主观视觉效果上，本文提出的算法能够重建出更接近真实的图像.在图4和图5中，对分别来自测试集BSDS100中的“37073”以及Urban100中的“image_093”的图像进行4倍放大因子的重建，从主观方面展示了几种重建方法的重建效果.由图4和图5可以看出，本文所提出的LCN算法与其他算法相比，不仅可以恢复出较清晰的边缘特征而且可以准确的重建平行直线和网格直线，重建后的图 片更加的接近于真实图片.

图4 “37073”四种算法重建的比较Fig.4 Comparison of four algorithm reconstructions for“37073”

图5 “image_093”四种算法重建的比较Fig.5 Comparison of four algorithm reconstructions for“image_093”

4 结论

本文提出了一种拉普拉斯金字塔结构的团网络超分辨率图像重建算法，用来解决SR问题.采用拉普拉斯金字塔结构，通过渐进式重建高分辨率图像的方式，逐步地优化重建结果.将残差学习应用到网络中，减少网络参数，避免梯度爆炸.同时，为了最大化层间交流，将CNB作为拉普拉斯金字塔结构的构建模块.在每个CNB模块中，任意两个卷积层之间既有前向又有反馈连接，层间信息交替更新，使层间信息流和反馈机制最大化，连接更加密集，提取到更多细节的特征.

在4个基准数据集上进行广泛的评估，实验表明本文提出的算法在图像客观评价指标PSNR与SSIM上，分别有0.05dB至0.36dB 与0.001 至0.006 的提升.在视觉质量上也取得了较好的效果，不仅消除了重建伪像，在对边缘以及线条的重建上更是取得了较好的结果，更加适用于通用的图像.但是本算法所用的参数较多，当网络基本构建模块CNB的个数以及层数增加到一定量时，仅靠残差学习无法消除梯度爆炸带来的重建质量下降问题，因此有待进一步改进算法.