浅谈如何让数学阅读走进倍数关系
2019-08-11洪玉森
摘 要:数学成绩不理想,大部分是因为阅读能力较弱,看到题目较长就不知道怎么办,信息一多就不知该如何取舍。因此,怎么样进行“数学阅读”已成为急需解决的问题。
关键词:阅读;倍数关系;模型
阅读对于学习来说是一件非常重要的事情,学习数学同样也需要学生进行必要的阅读。在解决有关倍数问题的时候,不能清晰地理解倍的含义,建立倍的模型,导致片面地见“倍”就乘。学生特别容易混淆“求一个数是另一个数的几倍”和“求一个数的几倍是多少”这两个问题,学生对于这两类题目审题不清,归根结底还是学生的数学阅读能力差。数学信息包括文字信息、符号信息、图形信息。学生进行数学阅读,不仅要会阅读数学文字语言,还要学会阅读数学图形语言,并能利用已有的知识和经验,对数学文字信息和图形信息进行相互转化,能更好地学习“倍”。学生可从以下3个部分,阅读倍数问题的教材。
一、 认识“倍”的概念
教材是数学学习最好的阅读材料,从教材的情境图中,学生可以运用之前所学的知识从情境中提取数学信息,将数学图形语言转化为数学文字语言。学会发现新的问题,也是学生对所学知识进一步升华的开始。
例如:教学倍的定义的情境图,图中有不同颜色的萝卜,学生在一年级下册学习过“分类与整理”。在探究倍的含义前,出示情境图,引导学生带着问题,进行数学信息的搜集:“图中有几种萝卜,每种各有几个,将其画出来”;仔细阅读数学图形语言,对其进行分类整理后,学生根据所画的分类结果,说说“红萝卜和胡萝卜的根数关系、胡萝卜和白萝卜的根数关系”;学生已经会比较两个数量的差,初步观察后比较:红萝卜和胡萝卜的根数差,胡萝卜和白萝卜的根数差,红萝卜和白萝卜的根数差。
学生根据乘法的意义,在“几个几”的基础上认识倍。学生通过看一看,比较胡萝卜(2根)和红萝卜(6根)的数量关系:红萝卜:2根;胡萝卜:6根有3个2根,引出一个数的几倍的含义,可以说红萝卜的根数是胡萝卜的3倍。再引导学生以胡萝卜2根一份为基础,将白萝卜每2根一份圈一圈,用“几个2根”来形容胡萝卜和白萝卜两个量的关系,思考并说一说:“红萝卜:2根;白萝卜:10根,有几个2根”。“有5个2根,可以用一句怎样的话来描述。”体会几个几与倍的关系,进一步理解倍的概念。
学生初步建立起倍的概念后,进行变式练习:如果小兔子吃掉一根红萝卜,学生通过动手操作,摆一摆,思考剩下的红萝卜(5根)与白萝卜(10根)的根数关系;再变换情境:小兔子又吃掉1根红萝卜,比较剩下的红萝卜(4根)胡萝卜(2根)之间的根数关系。
根据情境图,圈一圈,摆一摆,形象生动地展示了两个数量之间的倍数关系,引导学生理解“一个数里包含几个另一个数”,也就是说一个数是另一个数的几倍。
二、 求“一个数是另一个数的几倍”问题
“几何直观”在《数学课程标准》被定义为:“主要是指利用图形描述和分析问题。”借助几何直观可以把抽象的数学问题变得直观、形象,有助于探索解决问题的思路。而倍是个抽象的概念,是两个数量之间的关系,看不见摸不着,学生较难理解,在图形的帮助下,学生能更好地分析问题,解决问题。
教学例2:擦桌椅的有12人,扫地的有4人。擦桌椅的人数是扫地的几倍?学生阅读题目后,将搜集到的数学信息,归纳为两个条件:擦桌椅的有12人和扫地的有4人,一个问题:擦桌椅的人数是扫地的几倍?再引导学生画出直观形象图:
扫地的人: ○○○○
--!>
擦桌椅的人:
扫地的人:
学生画完形象图后,借助直观的形象图分析数量。以扫地的人数(4人)为标准,画一画,看一看擦桌椅的人数(12人)里面有几个标准(4人),问题:求擦桌椅的人数是扫地的几倍?就是求12里面有几个4,转化为学生学习过“一个数里有几个几,用除法计算”。
借助形象图,直观形象地展示其数量,并分析其数量关系,学生能理解用“除法计算”的算理。建立起“求一个数是另一个数的几倍”,就是求一个数里面包含几个另一个数,用除法计算。
三、 求“一个数的几倍是多少的问题”
数学家华罗庚曾经说过:“数缺形时少直觉,形少数时难入微。”除了借助画图的办法,还可以数形结合,将数学的文字语言转化为数学的图形语言,化抽象为具体,帮助理解、分析题意。
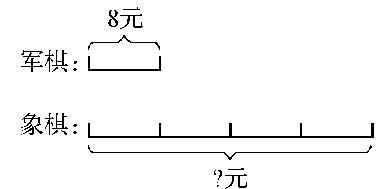
教学例3:军棋的价格是8元,象棋的价格是军棋的4倍。象棋的价钱是多少元?学生已经知道,“求几个相同加数的和”与“求几个几是多少”都可以用乘法计算。学生阅读题目后,将会搜集到两个信息:军棋的价格,还有军棋价格与象棋价格之间的关系;一个问题:要求象棋的价格。理解以军棋的价格(8元)为1倍数,引导学生画线段图:
观察线段图,一眼可以看出,以军棋的价格(8元)为标准即1倍数,象棋的价格是军棋的4倍,也就是说有4个8元。将问题转化为“求4个8是多少”或“求4个8相加是多少”的问题,学生自然就会选择用乘法来解决。
学生通过数学阅读图形,从数学情境中,提取数学文字语言,抽象出倍的内涵,建立起倍的模型。在学习“求一个数是另一个数的几倍和求一个数的几倍是多少”这两个问题前,学生先认真阅读教材,再借助几何直观,将其转化为图形语言,把题目提供的信息转化为图形之间的关系,再利用已有的知识经验,进行问题的分析和解答,降低解決问题的难度。
参考文献:
[1]沈如磊,胡廷香.“几何直观就在我们身边”.吉林教育,2013.
作者简介:
洪玉森,福建省漳州市,漳州市实验小学。
