基于形状直径函数的三维模型集一致性分割算法研究

贾晖 张建刚

摘要：为了有效提高对三维模型集进行一致性分割算法的准确率和效率，提出一种三维模型集一致性分割算法。该算法基于形状直径函数特征和谱聚类方法。首先计算模型各个面片的形状直径函数特征（SDF）特征;其次计算模型各面片之间的形状相似性，形成相似性矩阵。最后采用谱聚类算法对模型集进行一致性分割。将本文算法与相关方法进行对比，实验结果表明，本文算法能准确的对一致性分割数据集中的若干模型进行有意义的分割，使得分割部位具有一定的对应关系，且面片平均划分准确率较好。

Abstract： In order to improve the accuracy and efficiency of the algorithm of 3D model set consistency segmentation， an algorithm of 3D model set consistency segmentation is proposed. This algorithm is based on Shape diameter function（SDF） and spectral clustering. At first， The face SDF characteristics of each models in the model set is extracted; and then The similarity between each face of the model is calculated， and the similarity matrix is formed. At last utilize the spectral clustering algorithm to segment the model set consistently. The algorithm in this paper is compared with the relevant methods， the experimental results show that the proposed algorithm can accurately segment several models in a consistent data set， make the segmentation parts have a certain correspondence， and the average segmentation accuracy is better.

关键词：三维模型;一致性分割;形状直径函数;谱聚类

Key words： 3D model;consistency segmentation;SDF;spectral clustering

中图分类号：TP391                                      文献标识码：A                                  文章编号：1006-4311（2019）17-0277-03

1  概述

三维模型有意义的分割是根据模型的几何特征将模型分解成为有意义的连通子部分[1]。单个模型由于分割尺度的不同造成分割结果的不一致，难以实现模型重用。

近年来模型集的一致性分割成为研究热点[2][3]。Van Kaick[4]提出了模型集一致性分割的定义。设模型集上有n个模型，构建模型集上各模型分割部位之间的关联关系R。可以证明模型集上部位之间的关联关系具有自反、对称和传递性，是等价关系。三维模型集的一致性分割就是基于该等价关系进行的。与单个模型分割相比一致性分割的优势是由于所有模型有着相同的分割尺度，所以有利于分割结果的重用和比较。一致性分割算法更具有实用性，被广泛应用于快速建模[5][6][7]及三维数字模型重建[8][9][10]。

在三维模型的一致性分割方法中，聚类算法是模型分割的主流方法。特征的选择不能选用如曲率法线方向等表面特征，因为相似的部位可能会因为姿态的变化而有不同的表面特征，使得分割误差增大，分割效果下降。

本文采用形状直径函数[11]（SDF）特征及谱聚类方法对整组模型集进行一致性分割。将三维模型看做带权无向图，面片看做图的结点，面片与面片之间的特征相似性关系看做图的边。将面片的分割问题，看做图的分割问题。首先提取模型集中各个模型面片的SDF特征，其次计算面片特征之间的相似性矩阵。最后采用谱聚类对三维模型进行分割。

2  SDF（形状直径函数）

形状直径函数（Shape Diameter Function SDF）最早由Shapira提出。該特征为模型的体特征，当模型变形时，曲率、法线方向、距离都会发生变化，但模型体积保持不变。适用于多个模型相似部位的特征划分。

SDF特征的计算方法如下：

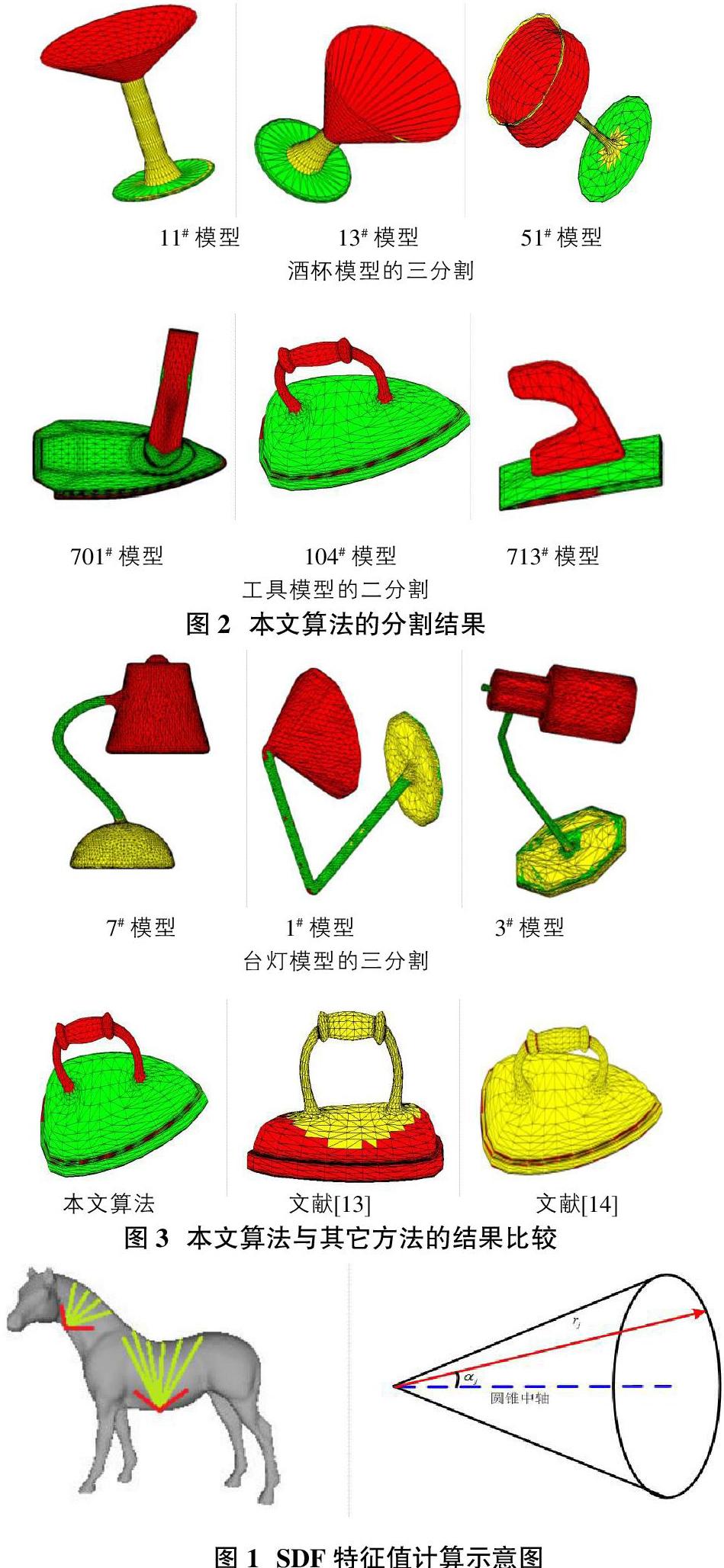
STEP1：从每个面片顶点以法线反方向为轴做圆锥。在圆锥内部，向法线反方向发射射线。

STEP2：计算射线平均长度、长度标准差和定义有效范围。分别用rm、？滓和range表示。

STEP3：若 定义权重 是rj与圆锥轴的夹角。面片顶点的SDF值计算公式为：

STEP4：计算各面片重心点的SDF值，利用公式（2）对重心点的SDF值归一化。其中？琢为归一化参数。

其計算示意图如图1所示。SDF特征和模型的体积相关，与表面特征如曲率、法线方向等特征无关。特别是姿态不同而体积相似的模型。如台灯模型集中各个台灯具有不同的底座，连接杆和灯头。各部位之间曲率特征不同但体特征相似。

3  基于SDF特征的谱聚类分割算法

本文研究一种一致性分割算法。该算法是基于谱聚类方法和形状直径函数特征的。谱聚类算法建立在谱图理论之上，将待聚类模型视为带权无向图。图的顶点为待聚类的面片，图的边权为面片之间的相似性关系，边权矩阵被称为相似性矩阵。利用谱图理论分析该无向图，找出分类结构。

3.1 相似性矩阵

模型面片之间的相似度的计算结果将显著影响谱聚类算法的准确性和有效性。面片距离越近，属于一类的概率越高，距离越远，属于一类的概率越低。模型体特征越接近，属于一类的概率越高，体特征差异越大，属于一类的概率越低。参考图像分割中计算像素的相似度方法[12]，采用公式（3）计算面片之间的相似度：

wij为面片i和面片j的相似度。？滓I是SDF特征的尺度参数。

3.2 稀疏化

相似度计算可得三维模型中任意两个三角面片的相似度。若模型集中所有面片的个数为n，则W为n×n维矩阵。此时图为n个结点的完全图。距离过大的面片属于一个划分的概率低。因此定义相似性计算距离ri，面片i到其它所有面片的测地距离，取其平均值确定相似矩阵的计算距离。 ，其中j=1…n。采用以下方法确定最终的相似性矩阵。d（i，j）为i面与j面的测地距离，以顶点间的测地距离的平均值来确定。

4  实验结果与分析

在Windows 上，实验数据集采用一致性分割数据集（COSEG），该数据集中具有多个大类的三维模型集，如四足动物、椅子、工具、台灯和酒杯等。每个模型集中又有若干个类似的三维模型。对三维模型的一致性分割提供很好的实验数据。算法运行环境为Intel Core i9 7900X CPU， 8GB内存， Microsoft Visual Studio 2010。

对杯子，工具和台灯模型集进行一致性分割。图2为本文算法的分割结果。从实验结果来看，面片被较准确的划分到相应的部位上去。错误划分的面片较少，划分部位较为完整。并且同类模型的分割结果具有一定的对应关系。如台灯模型的三分割中，模型被分成了灯头，连杆和底座。分割中也存在一定的误差，这跟模型的特征值计算误差有关。实验结果表明本文算法能准确高效的完成一致性分割。

图3为本文算法与文献[13]和文献[14]的分割效果对比。文献[13]采用AGD特征进行模型分割，能获得一定的部位信息，但分割结果不够准确。文献[14]采用离散曲率作为主要特征，能提取模型表面凹区域分割线，需要进行下一步的区域划分才能获得准确的部位分割结果。并且这两种算法都不能形成模型集上的一致性分割。本文算法不但能获得较准确的分割结果，而且对于整组模型的分割部位具有一定的对应关系。本文的分割算法更加适合进行部位重用和快速建模前的预分割。

模型的噪声对分割结果影响严重，在面片简化的过程中，表面特征会发生显著变化，但体特征则不会。本文算法与体特征相关，对于模型的简化有很强的鲁棒性。模型简化不会对模型分割效果产生影响。

5  总结

在本文算法中，首先计算模型集上各个三维模型的面片SDF值，作为特征向量;其次构建各个模型之间的相似性矩阵，根据距离越近属于一个分块的概率越高的原理对相似性矩阵稀疏化;最后利用谱聚类进行分割。实验结果表明对一致性分割数据集中多个具有类似形状的模型能够实现有意义的一致性分割，且分割结果良好。

另外，需要继续研究的问题是：分割部位数需要在算法执行前人工设定，扔不能根据特征的取值范围自动计算。对于体特征不明显的模型算法得不到较好的分割结果。

参考文献：

[1]Ngo D T ， Ostlund J ， Fua P . Template-Based Monocular 3D Shape Recovery Using Laplacian Meshes[J]. IEEE TPAMI， 2016， 38（1）：172-187.

[2]Kleiman Y， Fish N， Lanir J， et al. Dynamic maps for exploring and browsing shapes[J]. Computer Graphics Forum， 2013， 32（5）：187-196.

[3]Kalogerakis， Evangelos，Hertzmann， Aaron，Singh， Karan.

"Learning 3D mesh segmentation and labeling."[C]. ACM Siggraph. 2010.

[4]Oliver van Kaick，Hao Zhang，Ghassan Hamarneh et al. A Survey on Shape Correspondence[J]. Computer Graphics Forum， 2011， 30（6）：1681-1707.

[5]Averkiou M， Kim V G， Zheng Y， et al. ShapeSynth： Parameterizing model collections for coupled shape exploration and synthesis[J]. Computer Graphics Forum， 2014， 33（2）：125-134.

[6]Chaudhuri S， Koltun V. Data-driven suggestions for creativity support in 3D modeling[C]// Acm Siggraph Asia. 2010.

[7]Hang S， Maji S， Kalogerakis E， et al. Multi-view Convolutional Neural Networks for 3D Shape Recognition[C]// IEEE International Conference on Computer Vision. 2015.

[8]Kreavoy V， Dan J， Sheffer A. Model Composition from Interchangeable Components[C]. Conference on Computer Graphics & Applications. IEEE Computer Society， 2007：129-138.

[9]Mejia D ， Ruiz-Salguero O ， Cadavid C A . Spectral-based mesh segmentation[J]. International Journal on Interactive Design and Manufacturing， 2016：1-12.

[10]Lun Z， Gadelha M， Kalogerakis E， et al. 3D Shape Reconstruction from Sketches via Multi-view Convolutional Networks[J]. 2017.

[11]Shapira， Lior et al.Consistent mesh partitioning and skeletonisation using the shape diameter function. The Visual Computer 24.4（2008）：249-259.

[12]纳跃跃，于剑.一种用于谱聚类图像分割的像素相似度计算方法[J].南京大学学报（自然科学），2013，49（2）：159-168.

[13]Zhang， E. Feature-based surface parameterization and texture mapping. ACM Trans. Graphics 24.1（2005）：1-27.

[14]賈晖，耿国华，周明全，等.基于区域离散曲率的三维网格分水岭分割[J].计算机工程与应用，2015，51（11）：182-186.

作者简介：贾晖（1978-），女，陕西西安人，博士，讲师，研究方向为三维数字几何处理;张建刚（1977-），男，陕西西安人，硕士，高工，研究方向为智能信息处理。