R语言在几类优化问题中的应用
2019-08-10高成强


摘要:R语言以其免费、开源、灵活、扩展程序包丰富等优点,在工程及科研领域得到越来越广泛的应用。本文介绍了R语言的基本功能,并利用R语言的lpSolve、Rglpk、igraph扩展程序包来解决运筹学中的线性规划、整数规划、运输问题、最短路问题、最小生成树问题五类典型优化问题。
Abstract: R language is widely used in engineering and scientific research with its advantages of free, open source, flexible, and rich package. This paper introduces the basic functions of R language, and uses extended program package of lpSolve, Rglpk and igraph to solve four typical optimization problems in operations research, which are linear programming, integer programming, transportation problem, shortest path problem and minimum spanning tree problem.
关键词:R语言;优化问题;程序包
Key words: R language;optimization problems;program package
中图分类号:TP311.1 文献标识码:A 文章编号:1006-4311(2019)17-0238-03
0 引言
当前,在优化问题的科学计算中,使用较多的是商业软件如Matlab、Mathematica等,这类软件功能强大、应用方便,但也存在着价格昂贵、体积庞大等缺点。而R作为一款免费的开源软件,具有编程简单、体积小巧、数据分析功能强大、扩展性能好等特点,在很多应用场合可以替代商业软件。
1 R语言简介
R语言是一种自由软件编程语言与操作环境,主要用于统计分析、绘图、数据挖掘等。最初是由新西兰奥克兰大学的Ross Ihaka和Robert Gentleman开发,因此称为R,现在由“R开发核心团队”负责开发和维护[1]。
R是一个统计分析的环境,由于很多统计方法在估计和求解的过程中都需要用到大量的优化算法,因此R环境中自带了一些优化求解的函数,比如optim和constrOptim。此外,由于R是开源工具,因此可以借助很多第三方R包甚至其他的开源项目来实现很多优化问题的求解[2]。用户可以根据自己的需求编写脚本、R包,即便是没有任何编程功底,仅仅想使用也可以在CRAN社区(Comprehensive R Archive Network)上找到相对应的R包[3]。
2 几类优化问题的求解示例
由于R的基本库功能有限,优化问题的求解一般要使用扩展程序包,需要到R的CRAN社区下载程序包来扩展R的求解功能[4]。程序包的下载地址为:http://cran.r-project.org。
本文示例中所用到的程序包有lpSolve、Rglpk、igraph。
2.1 线性规划问题
例1:有一砌块生产厂家生产两种砌块,其中一种是有颜色的。每生产有色砌块1m3,需要2h机器时间、3h人工和2mm3颜料,利润是150元/m3;每生产无色砌块1m3,需要1h机器时间和4h人工,利润是90元/m3。现共有10h机器时间、24h人工和8mm3颜料,问每一种砌块生产多少,厂家所得利润最大[5]。
求解此问题,可设生产有色砌块x1 m3,生产无色砌块x2 m3,则此问题的优化模型为:
可使用lpSolve程序包中的lp( )函数进行求解,函数的语法可以参阅lpSolve文件。
求解此问题的R代码为:
目标函数z取得最大值即当有色砌块和无色砌块分别生产3.2m3和3.6m3时,厂家所得利润最大,最大值为804元。
对于无可行解的线性规划问题,lp( )函数也会给出提示。例如线性规划模型:
程序会给出结果Error: no feasible solution found,即认为模型有误,同时也说明线性规划问题无可行解。
2.2 整数规划问题
例2:某商场对售货员的需求经过统计分析如表1所示。
为了保证售货员休息时间,要求售货员每周工作5天,休息2天,且休息的2天是连续的,问应该如何安排售货员的休息时间,既能够满足工作需要,又使售貨员的人数最少[6]
2.3 运输问题
例3:某食品公司有A1,A2,A3三个面包生产厂,每月产量分别为7t,4t,9t;有B1,B2,B3,B4四个销售公司,每月销量分别为3t,6t,5t,6t。从第i个面包生产厂到第j个销售公司的单位运价(百元/t)如表2所示,问:该公司应如何调运,在满足各销售点需求量的前提下,使总运费最少[7]?
此问题为运输问题中的产销平衡问题。运输问题的本质也是一类线性规划问题,可以利用lpSolve包中的lp.transport( )函数进行求解。求解此问题的R代码为:
即A1向B1,B3分别调运2t,5t,A2向B1,B4分别调运1t,3t,A3向B2,B4分别调运6t,3t,此时总运费为85百元。需要说明的是,此问题的最优解不唯一。
对于产销不平衡问题,也可以利用lp.transport( )函数进行求解。
例4:某公司从两个产地A1,A2将物品运往三个销地B1,B2,B3,各销地的销量以及从产地到销地的每件物品的运输单价(元/件)如表3所示。问:应如何组织运输,使总运输费用最小?
此问题的求解与前述产销平衡问题类似,但需要注意的是row.signs和col.signs约束条件的选取,row.signs表示按行(产地)的约束条件,row.signs表示按列(销地)的约束条件。此问题中,row.signs = rep("=", 2),col.signs = rep("<=", 3)。
2.4 最短路问题
例5:里特城是一个农村的小镇,它的消防队要为包括许多农场社区在内的大片地区提供服务。这个地区有很多条路,从消防站到任何一个社区都有很多条路线。因为时间是到达火灾发生点的主要因素,所以消防队队长希望事先能够确定从消防站到每一个农场社区的最短路。
图1示意了连接消防站和其中一个农场社区的道路系统(长度单位为km),O为消防站所在地,T为农场社区所在地,求O到T的最短路径[8]。
此问题中,O为出发点,T为终点,最短路问题可使用igraph程序包进行求解,首先根据点、边、权,在程序中构建出网络,然后利用shortest.paths( )函数和get.shortest.paths( )函数求解最短路径。
2.5 最小生成树问题
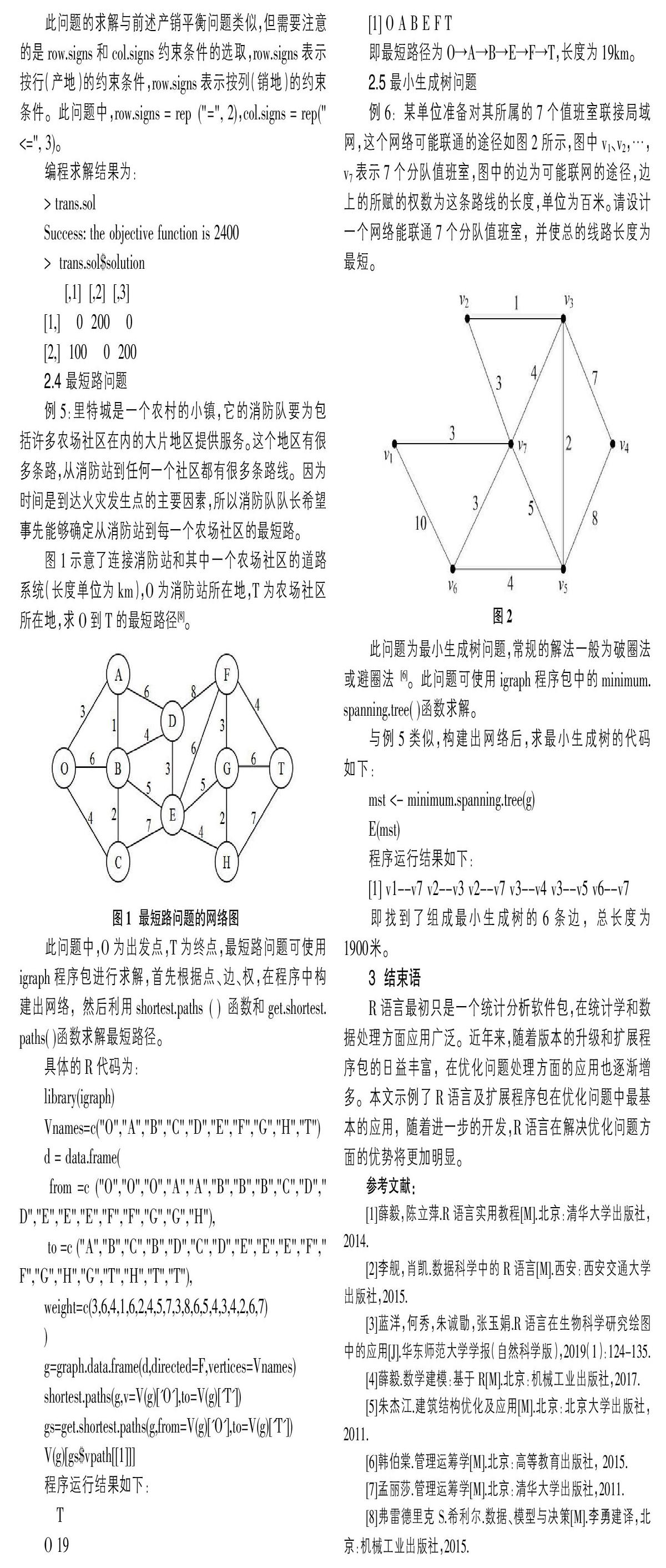
例6:某单位准备对其所属的7个值班室联接局域网,这个网络可能联通的途径如图2所示,图中v1、v2,…,v7表示7个分队值班室,图中的边为可能联网的途径,边上的所赋的权数为这条路线的长度,单位为百米。请设计一个网络能联通7个分队值班室,并使总的线路长度为最短。
此问题为最小生成树问题,常规的解法一般为破圈法或避圈法[6]。此问题可使用igraph程序包中的minimum.spanning.tree( )函数求解。
与例5类似,构建出网络后,求最小生成树的代码如下:
程序运行结果如下:
即找到了组成最小生成树的6条边,总长度为1900米。
3 结束语
R语言最初只是一个统计分析软件包,在统计学和数据处理方面应用广泛。近年来,随着版本的升级和扩展程序包的日益丰富,在优化问题处理方面的应用也逐渐增多。本文示例了R语言及扩展程序包在优化问题中最基本的应用,随着进一步的开发,R语言在解决优化问题方面的优势将更加明显。
参考文献:
[1]薛毅,陈立萍.R语言实用教程[M].北京:清华大学出版社, 2014.
[2]李舰,肖凯.数据科学中的R语言[M].西安:西安交通大学出版社,2015.
[3]蓝洋,何秀,朱诚勖,张玉娟.R语言在生物科学研究绘图中的应用[J].华东师范大学学报(自然科学版),2019(1):124-135.
[4]薛毅.数学建模:基于R[M].北京:机械工业出版社,2017.
[5]朱杰江.建筑结构优化及应用[M].北京:北京大学出版社, 2011.
[6]韩伯棠.管理运筹学[M].北京:高等教育出版社, 2015.
[7]孟丽莎.管理運筹学[M].北京:清华大学出版社,2011.
[8]弗雷德里克 S.希利尔.数据、模型与决策[M].李勇建译,北京:机械工业出版社,2015.
作者简介:高成强(1981-),男,河北邯郸人,讲师,研究方向为工程管理。
