玩转立方体

王耀杨

挑战立方体

看到这篇文章的标题，相信很多同學都会感到奇怪：立方体？我早看得不能再熟悉了！还有什么可玩的呢？

不要得意得太早哦，在这篇文章里，我们将尝试从一个全新的视角来欣赏立方体，并且由此提出一系列有趣的问题。试试看，你能解决其中几个问题？

让我们从立方体的体对角线方向去观察它。如图①，一个立方体有4条体对角线，选取其中任意一条，沿此方向正投影，会得到一个正六边形。这个正六边形由3个彼此全等的菱形组成，每个菱形都是一个正方形面的投影。

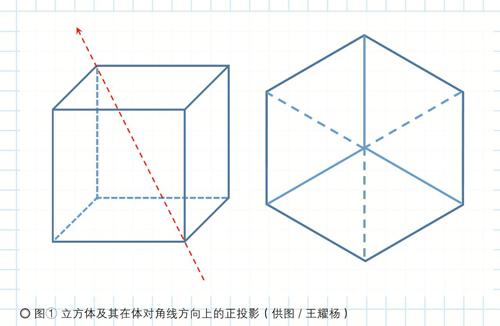
我们的第一个问题，就从这里开始：如果只用一只眼观察，最多同时可以看到不透明立方体的几个面，为什么？如果关注的对象是棱，那么最多同时可以看到几条棱，为什么？

第二个问题需要先定义“挖洞”的概念。当我们说“在一个立体图形上挖洞”时，意思是去掉一部分图形，同时保持剩余部分仍然具有一个完全的封闭形态，而不是类似“U”形。更进一步，当我们说“从挖好的洞中穿过”时，意思是在不超过洞边界的范围内行进，整个过程中不能破坏洞的边界。当然，我们始终假设所研究的图形都是刚性的，不会像橡胶那样发生弹性形变。现在问题来了：是否有可能在一个立方体中挖一个洞，使得另一个与它全等的立方体能够从洞中穿过去呢？

第三个问题：二维国的立方体来客。

1884年，一位英国牧师艾伯特写了一本名为《二维国》的小册子。作者的创作意图本不是宣讲数学，但是在今天看来，它完全可以作为一本现代几何学的入门科普书来读。所谓二维国，就是平面世界，其中的居民都是平面图形，如三角形、正方形或者圆。居民们关于空间的经验直觉就只局限于二维。那么，我们所熟悉的三维图形在这些居民的理解中会是怎样的存在呢？

设想一位立方体先生到二维国亲戚家拜访，后者当然无法窥见立方体的全貌，而只能看到立方体穿过二维平面时所截得的“侧影”。例如，当立方体的一组棱垂直于平面时，截得图形恒为正方形;当立方体的面对角线垂直于平面时，留下的是宽度不断变化的矩形“侧影”，如图②：穿入和穿出瞬间时，退化为线段的形态，其间最大矩形截面的长宽比为为。

现在问题来了：如果令立方体的体对角线垂直于平面，则穿行时所留下的“侧影”会如何变化？

在各位读者自己开始研究之前，这里有一个建议。你要保证手头有一个立方体的实物模型，最好是透明的;比如用小细棍和胶泥之类的材料做一个，便于观察。上面这几个问题几乎都是基于观察具体实物来研究的，当然，你还需要解释其中的道理。

艺术家与立方体迷思

在给出问题1的解答之前，我要先考考读者们，你们能否想象，对这个问题的追问和深思居然激发了一群艺术家的创作灵感？难道说艺术家们也都很喜欢数学？

问题1的答案是：最多同时看到3个面;最多同时看到9条棱。

立方体的6个面可以分成3组，每一组都有彼此相对，即没有公共点的两个平行面。从体对角线方向可以同时看到3个面，我们来证明不能看到更多。假设可以看到4个面，则必定有一组平行面同时被看到，但这是不可能的。设想它们是发光的（“看到”的物理原理就是来自被看物体的光子进入人眼），则一组平行面照亮的空间区域分别位于两个平行平面的一侧，而这两个区域没有公共点，如图③所示。换言之，空间中任何位置都不能同时看到这两个面。因此3个就是能同时看到的最多面数。

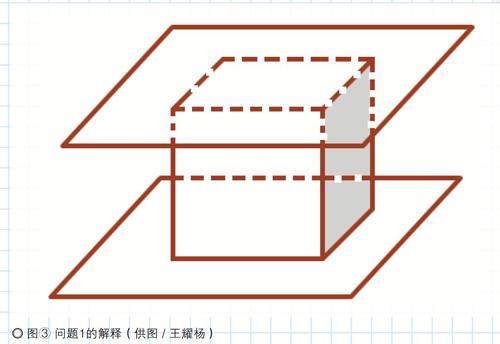
由前面的分析可知，3组中每组都至少有一面是看不到的，这3个看不到的面两两相交得到的3条棱肯定也是看不到的，因此最多同时看到12-3=9条棱。沿体对角线方向确实可以看到9条棱，因此9条是能同时看到的最多棱数。

但是这与艺术创作有何关联呢？原来，20世纪初的艺术家们也采纳了将现实物体分解成局部要素的几何思维，但是他们不满足于用只能看到有限个侧面的单一视角呈现，而是尝试将多视角的景象在同一个画面中展示出来。这就是影响深远的立体派（Cubism），这一思潮首先影响的是画家和雕塑家，很快又波及到文学、音乐和建筑领域。

图④给出了立体派代表人物毕加索的两幅作品。其中左图是较早的作品《弹曼陀铃的少女》，可以看到原本婉转流畅的线条都呈现为看似彼此割裂而抽象的几何图形;右图则是相对晚一些的作品《静物》，画面看似混乱，是因为画家将原本不可能从任一视角看到的各种细节全都呈现出来。这两幅作品可以代表毕加索个人思考的两个阶段：前者是“分析”的时期，后者则是“综合”的时期。

问题2需要一点初中水平的数学计算。前文提到過，将立方体沿体对角线方向投影，可以得到一个正六边形。如图⑤，为不失一般性，设立方体边长为1，则正六边形的较短对角线（垂直于视线方向的面对角线保持原长），如图建立直角坐标系，则有。由此确定直线方程，代入坐标验证，可知A点位于AB下方;结合对称性可知正方形位于正六边形内部。将图示正方形对称地扩大一点点，还可以位于正六边形内部，由此可以保证原正方形可以从中穿过去。

让一个高度对称的立体图形从自身之中穿过去，乍看起来似乎是匪夷所思的，但是上面这个例子恰好使我们意识到立方体具有一种特别的对称性：体对角线。不难想象，如果将立方体换成具有完美对称性的球，那么问题2就无解了。因此不妨说，立方体能够实现这个结果，恰恰是因为它还不够对称。按照这一思路，那么正四面体也可以穿过自身吗？请读者自己寻找答案吧。

问题3相当于考察垂直于体对角线的不同平面截立方体所得的图形。最开始是一个点，接着变成正三角形并逐渐放大，正三角形的面积达到最大后各顶点内缩而变成六边形，到恰好正中间位置时截面是一个正六边形;后一半变化过程是对称的，如图⑥。

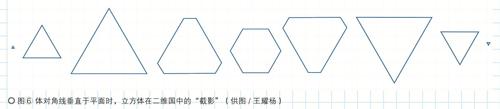
在今天，如果一位数学教师对艾伯特牧师的《二维国》感到格外欣赏，主要原因很可能是因为它为初学者探索四维几何学打开了一扇门。一位二维国居民能够以何种方式去思考和理解三维世界来的客人，恰如我们三维智慧生物可以如何去思考和理解四维的存在。

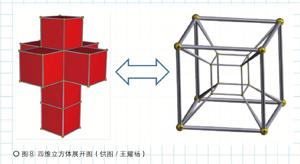
如果你以为四维几何是只有数学家们才会关注的奇思妙想，图⑦中的画作可能会令你大吃一惊。1954年，超现实主义画家达利完成了一幅前所未有的《耶稣受难》，这可能是同主题作品中最具视觉冲击力的一幅，因为其中出现了四维立方体在三维世界中的“展开图”。正如三维立方体的展开图是由6个正方形构成的平面图形，四维立方体的展开图是由8个三维立方体构成的立体图形—你不妨试着想想它“拼合”起来的样子（如图⑧）！

各位读者，相信你们已经看到，立方体的体对角线是一个极为特别的视角;从这个角度考察立方体，会出现很多有趣的新问题和新成果。作为本文的结束，这里给出一个趣味问题供有兴趣的读者研究吧。图⑨给出一个立方体型电阻，它的每条棱都是阻值为1欧姆的电阻，在体对角线两端连接外部电路，则整个立方体可以视为一个复合电阻。根据立方体的对称性质分析一下，它相当于多少欧姆的电阻呢？

答案与解析：5/6欧姆。假设整体复合电阻的外接端点是A和B，则由几何对称性可知A的

3个相邻端点确定了一个等电势面，位于A与等电势面之间的3个1欧姆电阻相当于并联关系，因此相当于一个1/3欧姆的电阻;下一个等电势面是，它与面之间的6个单位电阻相当于并联关系，因此等价于一个1/6欧姆的电阻;类似地，面与顶点B之间也相当于一个1/3欧姆的电阻。因此总电阻为1/3+1/6+1/3=5/6欧姆。

（责任编辑/陈莹  美术编辑/胡美岩）