横风作用下高速铁路桥梁全封闭声屏障气动特性的风洞试验研究

韩 旭，彭 栋，向活跃，李永乐，曾 敏，蔡理平

(1.西南交通大学 土木工程学院,四川 成都 610031;2.中铁第四勘察设计院集团有限公司，湖北 武汉 430063;3.广铁(集团)公司江门工程建设指挥部，广东 江门 529000)

随着我国高速铁路的发展，噪声问题越来越受到人们的关注。在自然和动物保护区等特殊地区的高速铁路，对噪声的控制提出了更高要求。目前，声屏障是防治铁路噪声的主要方法，包括4种类型：直立式、折檐式、半封闭式和全封闭式[1]。前3种声屏障应用相对较多，多用于居民聚集区[2-3]，而全封闭式声屏障应用较少。全封闭声屏障在运营过程中会受到横向风和压力波的作用。压力波主要受断面阻塞度、列车运行速度、列车长度等因素的影响。全封闭声屏障形状与隧道类似，在设计时可参考TB 10621—2014《高速铁路设计规范》[4]中高速铁路隧道断面面积的相关规定，因此本文计算时未考虑全封闭声屏障的压力波。桥梁全封闭式声屏障结构特殊，风荷载的确定没有相关参考依据，且桥梁离地一般较高，风荷载相对较大[5-6]。因此，有必要研究桥上全封闭声屏障的横风气动特性。

在已有研究中，Honda等[7]通过全桥风洞试验对设置声屏障时预应力混凝土斜拉桥的风致响应进行了研究。Holmes等[8]采用风洞试验方法对声屏障的风荷载进行了研究，分别对有无声屏障对桥梁气动性的影响进行了分析。郑史雄等[9]通过数值模拟和风洞模型试验对声屏障的风荷载体型系数进行了研究，并分析了声屏障位置和高度对全封闭声屏障体型系数的影响。Xiang等[10]采用风洞试验的方法，测试了声屏障后侧的流场分布，并分析了线路和声屏障高度的影响，还通过数值模拟方法得到了列车风作用下声屏障瞬态风荷载[11]，进一步分析了声屏障表面的压力分布。拉有玉、王争鸣等[12-13]通过风洞试验对兰新铁路第二双线上设置的防风明洞这一措施进行了研究，得到了防风明洞表面压力分布情况和结构整体风荷载。郭春等[14]通过数值模拟方法研究了兰新线路基防风明洞的横风气动特性。然而，兰新线的防风明洞在洞壁有一定的开孔，而全封闭声屏障为了达到降噪效果，需保证全封闭声屏障完全封闭。

综上可知，国内外主要采用风洞试验和数值模拟方法，针对直立式、半封闭式等声屏障研究列车风和自然风作用下的声屏障气动荷载。对于桥上全封闭声屏障横风气动特性风洞试验的研究较为少见。本文采用风洞试验的方法对桥梁全封闭声屏障在横风作用下的三分力系数和表面风压进行测试，分析风速、雷诺数效应、风攻角、侧视断面位置对全封闭声屏障横风气动特性的影响。

1 模型风洞试验

深茂(深圳—茂名)铁路通过广东新会“小鸟天堂”，为控制噪声在可接受范围内，不影响鸟类的繁殖栖息，在小鸟天堂北侧一定范围内的桥梁上设置了全封闭声屏障，全长2 km，其断面形状如图1所示。全封闭声屏障主要由立柱和吸声板组成，其中立柱由3段圆弧构成。桥址区靠近沿海地区，地势低平，平原开旷，大风天气时有发生，100年一遇的10 min平均基本风速为32.6 m/s。全封闭声屏障的横风荷载是声屏障设计的控制性因素之一。

图1 全封闭声屏障断面(单位：mm)

由于桥梁和全封闭声屏障的长度较长，属于线状结构，可以采用节段模型风洞试验进行研究。风洞试验在XNJD-3工业风洞进行，该风洞试验段长36 m，宽22.5 m，高4.5 m，风速为1.0～16.5 m/s，来流最大湍流强度小于1.5%。模型的缩尺比为1/20，桥梁模型总长度为3.46 m，宽度为0.65 m，高度为0.62 m。本桥桥墩实际最大高度为17 m，故节段模型的主梁离地高度为0.85 m。为了减少边界效应的影响，全封闭声屏障测试段取节段模型的中间位置，长度为0.69 m。为方便制作节段模型，忽略了全封闭声屏障表面的细节，简化后的全封闭声屏障断面如图2所示。安装于风洞实验室的节段模型如图3所示。其中，α为来流风攻角；β为风压测点的角度；CH，CV，CM分别为体轴坐标系下的阻力系数、升力系数、力矩系数；U为来流风速；L为测试段的长度。

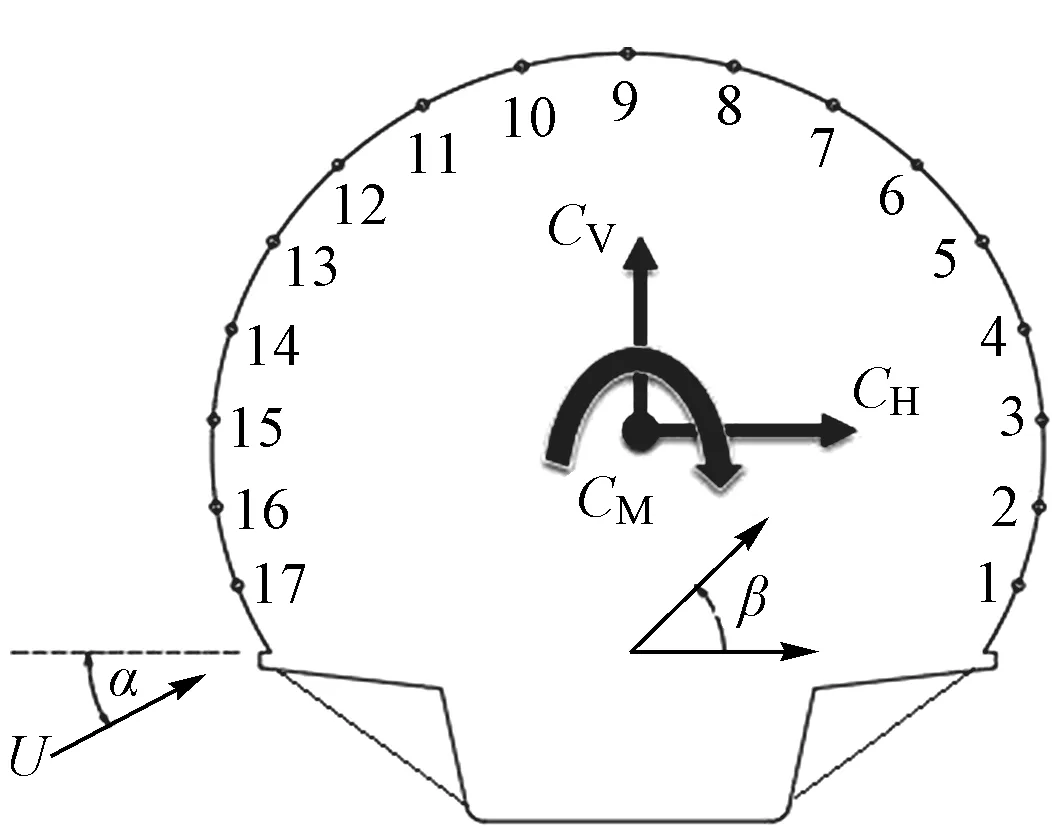
图2 简化后的全封闭声屏障断面

图3 试验中的节段模型

对全封闭声屏障的静力三分力测试时，综合考虑测力天平量程及测量精度。采用5 kg天平测试全封闭声屏障的三分力系数，天平安装在全封闭声屏障内部，作用点距桥面高度为0.217 m。测试段全封闭声屏障与两侧全封闭声屏障分离，底部封闭后与桥面分离，仅与固定在桥面上的天平连接。

三分力系数可以反映结构的整体风荷载，但不能反映风荷载的分布情况，需对全封闭声屏障表面的风压进行测试。试验时声屏障模型与桥梁模型为一整体，测压点均匀分布于节段模型断面内，间隔为10°，共17个测压点(参见图2)。在桥轴线方向，设置3个测压断面，每个断面间隔20 cm(参见图3)。在模型前方来流处安装了皮托管，用于测试来流静压。在模型两端设置高度为4.0 m的端板，用来支撑节段模型并减小节段模型端部绕流的影响。

为研究雷诺数效应的影响和验证测试结果的准确性，试验中进行了4级风速的试验，风速分别为6，8，10，12 m/s；每级风速下共测试了3种风攻角，分别为-3°，0°和3°。

2 数据处理

全封闭声屏障测力试验时，为降低试验误差，每级风速下各工况均测试2次，测试时间为50 s，采样频率为 2 000 Hz。得到全封闭声屏障的静力三分力系数[11]表达式为：

(1)

(2)

(3)

式中：FH，FV，M分别为阻力、升力和力矩；ρ为空气密度；D,B分别为节段模型的高度和宽度，本文模型设置为D=0.483 m，B=0.69 m，L=0.69 m。

进行全封闭声屏障测压试验时，每级风速下均测试3次，每次采集样本长度为 3 000，再通过平均处理得到全封闭声屏障表面风压力。通过下式得到风压系数CP[14-15]：

(4)

式中：P为全封闭声屏障表面压力；P∞为来流静压。

3 试验结果

3.1 风速的影响

为了研究风速对全封闭声屏障整体的气动力影响，图4给出了α=0°，风速为6～12 m/s时的三分力系数，以及全封闭声屏障表面的风压分布。

图4 不同风速下全封闭声屏障三分力系数和风压系数

由图4可知，随着风速的增加，全封闭声屏障的阻力系数有所降低，而升力系数明显增加，高风速时全封闭声屏障具有高升力的特点。全封闭声屏障断面为弧形，表面较为光滑，雷诺数效应对气流经过全封闭声屏障顶面时分离点的位置有较大影响。当风速较小时，气流的分离点靠近全封闭声屏障顶部的迎风侧，根据伯努利方程可知，此时全封闭声屏障顶部的风速较小，压力较大，所以升力系数小，而阻力系数大。随着风速的增加，分离点向全封闭声屏障顶部的背风侧移动[11]，此时全封闭声屏障顶部的风速较大，而压力比较小，所以升力系数较大，而阻力系数减小。由雷诺数计算公式Re=ρUd/μ(其中，d为特征长度，μ为动力黏性系数)可知，风速由6 m/s增加到12 m/s时，雷诺数由1.83×105增加到3.66×105。结合图4可知，雷诺数效应对全封闭声屏障的升力系数有较为明显的影响，而对阻力系数和力矩系数的影响较小。

测力时要求全封闭声屏障为一个封闭的模型，所以在全封闭声屏障底部增加了一块木板，其与桥面间设置约5 mm的缝隙，以保证全封闭声屏障与桥梁模型分离。测力的模型与风压测试方法的模型有一定的差别，2种测试方法只能对阻力系数进行对比，可以判断测试结果的准确性，但无法对比升力系数和力矩系数。针对图4(b)中的风压系数，通过对阻力方向的风压进行积分得到整体气动阻力，再由式(1)得到阻力系数，并与天平测力结果进行对比，见表1。可知，2种测试方法所得阻力系数有一定差异，但误差在可接受范围内。结合图4可以看出:在不同风速下，β=60°～120°时风压系数变化最为剧烈，在此范围的压力与升力系数有较大关联;升力系数在风速由6 m/s升到8 m/s 时也具有较大突变，测压结果与测力结果的规律总体上比较对应。此外，与GB 50009—2012《建筑结构荷载规范》[16]中类似结构的风压分布相比，高风速时本文风压分布测试结果虽然有一定差异，但变化规律基本相似。

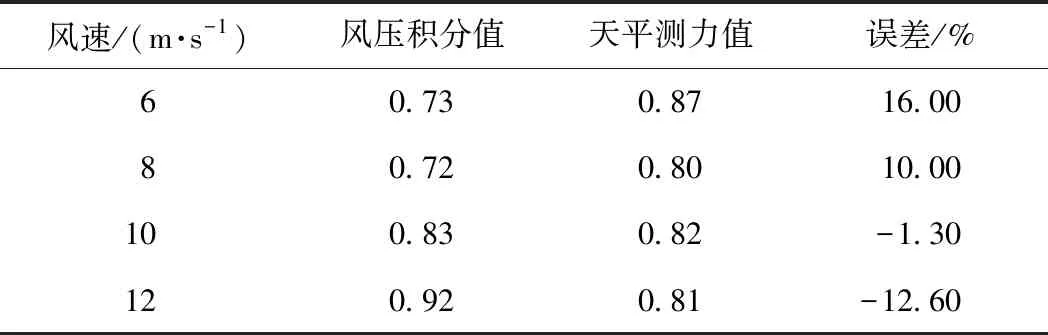
表1 阻力系数的不同测试方法对比

注：误差=(天平测力值-风压积分值)/天平测力值。

3.2 风攻角的影响

为了研究风攻角对全封闭声屏障气动特性的影响，针对-3°，0°和3°这3种风攻角的工况，测试了全封闭声屏障的三分力系数。风攻角对全封闭声屏障三分力系数的影响见图5。可知：①3种工况下阻力系数均随风速的增加总体呈降低趋势；②风速相同时，阻力系数总体上随风攻角的增加而减小；③风攻角对升力系数和力矩系数的影响相对较小；④3种工况下升力系数均在6～8 m/s时出现较大的突变，风速达到8～12 m/s 后，阻力系数和升力系数的变化均趋于平稳。说明不同风攻角条件下，随着雷诺数的增加，全封闭声屏障的气动力系数和风压分布系数有相似的变化规律。

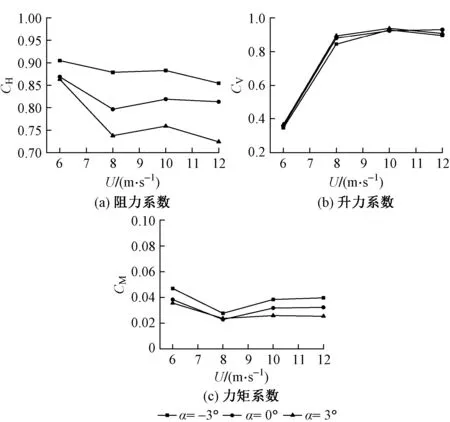
图5 风攻角对全封闭声屏障三分力系数的影响

图6 风攻角对全封闭声屏障风压的影响

当风速为12 m/s时，风攻角对全封闭声屏障风压的影响见图6。可知：①在全封闭声屏障顶部位置，α=0°时的风压系数最小，此时的升力系数最大(见图5(b));②在全封闭声屏障的迎风侧，α=-3°时的风压系数最大，而在全封闭声屏障的背风侧，α=0°时的风压系数最小。通过全封闭声屏障的前后压力差可求得阻力系数，其变化规律总体上与天平测力结果吻合。由此可见，风攻角对整个全封闭声屏障表面的风压分布均有一定影响。

3.3 全封闭声屏障风压沿顺桥向的分布

由于天平测力的方法难以得到沿顺桥向的气动力分布，因此采用测压的方法研究全封闭声屏障风压沿顺桥向的分布情况。当风速为12 m/s时，不同断面位置的风压系数见图7。可知：①全封闭声屏障3个断面的风压分布总体一致，中间断面的风压系数基本上处于另两个断面风压系数的中间；②在全封闭声屏障正上方附近(β=90°)，3个断面的风压系数差别稍大，原因是全封闭声屏障形状对雷诺数效应非常敏感，模型加工精度、风速沿顺桥向的分布不均匀性等可能导致测试结果有一定的差异。

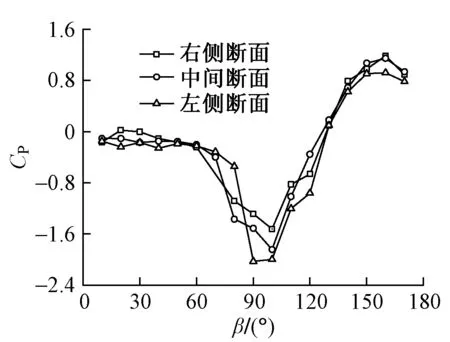
图7 不同断面位置的风压系数

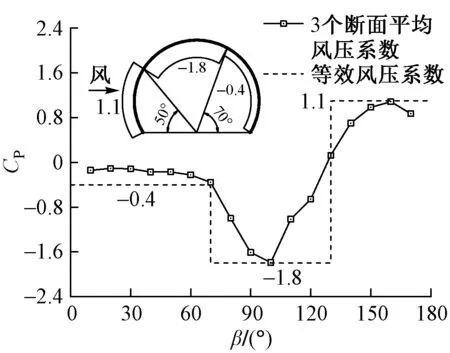
图8 等效风压系数

全封闭声屏障通常由多块吸声板拼接而成，采用风压系数更便于反映声屏障受力的变化，但风压系数在断面内分布较为复杂，沿顺桥向方向分布也有一定差异，因此直接采用图7中的结果用于设计时有诸多不便。由于全封闭声屏障通常较长，不同断面风压系数曲线具有相同的变化趋势，可采用等效风压系数将其简化为二维结构。结合GB 50009—2012，对图7中3个断面的风压系数取平均数后，将全封闭声屏障断面的风压分布划分为3个区域(如图8所示)，取每个区域平均风压系数的最大值作为断面的等效风压系数。3个区域的划分节点为70°和130°，当β< 70°时，风压分布较为均匀，β= 130°时接近正负压力交替位置。由图8可知，在全封闭声屏障的迎风侧、顶部和背风侧，风压系数可分别取1.1，-1.8和-0.4，而规范[16]中对应值分别为0.8，-0.8和-0.5。迎风侧和顶部的风压系数绝对值均比规范绝对值大，一方面与试验的雷诺数和桥梁的干扰有关，另一方面与结构的形状有关。关于结构形状，可采用数值模拟与代理模型结合[17]的方法进行气动外形的优化。

4 结论

通过缩尺比为1/20的节段模型风洞试验，测试了全封闭式声屏障的三分力系数以及表面风压分布。通过对比分析试验结果，得出以下结论：

1)全封闭声屏障节段模型的气动力和表面风压分布受雷诺数效应的影响较大；风速较低时，全封闭声屏障顶部为正压，风压系数和升力系数均较小；当风速较高时，全封闭声屏障顶部存在较大的负压和升力系数。

2)风攻角对阻力系数有较大影响，对升力系数和力矩系数的影响较小;对全封闭声屏障表面的风压系数有一定的影响，且变化规律较为复杂。

3)全封闭声屏障表面风压系数沿顺桥向的变化规律总体上一致，可划分为3个区间。简化后在全封闭声屏障的迎风侧、顶部和背风侧，风压系数可分别近似取1.1，-1.8和-0.4。