既有混凝土梁桥加宽改造的时变可靠度分析
2019-08-08白应华段展鹏刘均利
白应华,段展鹏,刘均利
(1.湖北工业大学 土木建筑与环境学院,湖北 武汉 430068;2.广西岩土力学与工程重点实验室,广西 桂林 541004)
迄今国内外对既有桥梁的可靠性分析进行了广泛研究。贡金鑫等[1]提出一种抗力随时间变化的时变可靠度模型,计算过程简便。田浩等[2]基于FORTRAN平台根据响应面法理论建立了新的可靠性指标分析方法,并对某桥在劣化环境作用下构件力学性能演变过程进行了分析。金浩等[3]基于蒙特卡洛理论研究了既有桥梁在4种不同加固改造方案下的可靠度。王磊等[4]针对目前桥梁可靠性评估样本少的问题建立了小样本下的可靠性指标评估方法,并以某装配式桥为例详细分析该方法具体评估过程,通过评估结果发现,钢筋锈蚀率及混凝土强度损失率对可靠度评估的影响最为明显。林辉等[5]根据验算点法理论,基于MATLAB平台对某钢筋混凝土桥的时变可靠度进行了分析,发现桥梁在整个服役期中,中期下降幅度最为缓慢,同时混凝土的开裂对桥梁可靠度影响明显。
既有桥梁桥宽不满足交通量要求时往往进行加宽,即在其一侧或两侧新建桥梁并与既有桥梁连成整体共同受力。学术界对其加宽改造前后结构的可靠性分析理论尚未建立起完善的体系。鉴于加宽前后新旧桥梁在劣化环境下刚度退化不一致对横向分布系数的影响,本文建立了既有桥梁加宽改造后结构时变可靠度分析模型,并以一座预应力混凝土梁桥加宽改造项目为例,分析了既有桥梁加宽后新、旧桥刚度劣化不同步对结构时变可靠度的影响。
桥梁在设计计算中必须考虑多种荷载作用,其中的恒载和活载产生的作用已取得完善统计资料[6-7]。车辆荷载冲击系数和横向分布系数的统计资料参考了美国相关标准的研究结果[8-9]。
1 钢筋混凝土构件劣化模型
在自然环境作用下混凝土构件保护层碳化可导致桥梁梁板内钢筋发生锈蚀,进而对构件的各种力学性能产生影响。本节结合以往对混凝土碳化以及钢筋锈蚀的研究成果,建立在劣化环境作用下的计算模型。
1.1 钢筋开始锈蚀模型
混凝土的抗压强度是混凝土综合质量的反映,其与混凝土的抗碳化能力具有密切关系。文献[10]将其作为反映混凝土碳化深度的主要参数,并考虑环境影响因子对碳化深度的影响,结合以往试验和工程案例建立起计算碳化深度的半经验半理论公式[10]:
(1)
式中:x为该钢筋开始锈蚀模型下混凝土发生碳化预测深度值,mm;kmc为该模型不定性系数,服从N(0.996,0.355)正态分布;fcuk为混凝土立方体抗压强度试验标准值,MPa;kj为钢筋碳化部位修正系数;kCO2为二氧化碳浓度影响系数;kp为浇筑面修正系数,对浇筑面取1.3,非浇筑面取1.0;ks为混凝土应力影响修正系数,受拉时一般取1.2,受压时一般取1.0;T为自然环境的年温度统计均值,℃;RH为自然环境下的年相对湿度统计均值,%;t1为暴露时间,年。
实际工程检测发现,碳化深度是否达到钢筋表面并不能完全决定钢筋是否锈蚀。徐善华等[11]对大量碳化试验数据和工程实测结果拟合获得钢筋开始锈蚀时表面到碳化位置最近距离预测模型,并将该距离参数定义为碳化残量。
x0=4.86(-RH2+1.5RH-0.45)(c-5)×
(lnfck-2.3)
(2)
式中:x0为碳化残量;fck为混凝土抗压强度标准值;c为保护层厚度。
基于对碳化残量影响的考虑,钢筋表面开始发生锈蚀时间tini和碳化系数k之间的关系式为
tini=(c-x0)/k
(3)
1.2 钢筋锈蚀速率模型
徐善华等采用钢筋快速腐蚀的方法,并结合现场实测结果,拟合出保护层开裂前钢筋锈蚀速率与钢筋锈蚀深度、环境修正系数等变量之间的关系[11]:
式中:λc1和λc2分别为混凝土保护层碳化开裂前、后钢筋锈蚀的速率,mm/年;kR为环境修正系数,潮湿地区取3.0~4.0,干燥地区取1.0~2.0;fcu为混凝土立方体抗压强度设计值。
当构件保护层开裂前,根据现场实测结果拟合出锈蚀深度δc1(t)的预测模型为
δc1(t)=λc1(t-tini)
(6)
构件保护层开裂后,自然因素的作用会加快钢筋锈蚀,根据大量实测结果,此时的锈蚀深度δc2(t)的预测模型为
δc2(t)=δcr+λc2(t-tcr)
(7)
式中:δcr混凝土膨胀开裂时钢筋锈蚀的深度;t为结构的运营使用时间;tcr为混凝土膨胀开裂时间。
模型的均值系数为0.8,方差为0.6[11]。
1.3 锈蚀梁承载能力计算
牛荻涛[10]考虑到钢筋锈蚀对钢筋与混凝土界面黏结性能具体影响尚未完全弄清楚,因此引入协同工作系数对正常钢筋混凝土受弯构件承载能力计算公式进行改进,建立了针对锈蚀钢筋的计算模型:
式中:Msu为钢筋在保护层碳化后发生锈蚀后梁板的正截面受弯承载能力;fc为混凝土轴心抗压强度;b截面宽度;h0截面有效高度;fy为钢筋的屈服强度;Ase为钢筋的等效受拉面积。
(10)
式中:Asi为对应钢筋的截面面积设计值;ksi为对应钢筋与混凝土协同工作系数;αsi为钢筋锈蚀后对应钢筋的抗拉强度折减系数,其值为
式中:ηsi为锈蚀钢筋的截面损失率。
模型不定性系数服从N(0.996,0.099 7)的正态分布。
1.4 刚度计算
文献[12]通过对钢筋锈蚀的钢筋混凝土梁进行加载,发现钢筋锈蚀对主梁等效截面抗弯刚度会产生明显影响,并根据试验数据建立了钢筋锈蚀率ηs对截面开裂刚度Bs影响关系,具体模型如下
Bs=αB
(12)
式中:B为开裂截面的刚度值;α为钢筋混凝土构件保护层开裂截面刚度退化系数,其值为
(13)
式中:Mcr为钢筋混凝土构件界面开裂弯矩;Ms为其截面弯矩。
2 加宽后的时变可靠度分析
构件的时变可靠度指标β(Ts)指的是某一时间段[0,Ts]内的可靠度指标[13-15]。为获取[0,Ts]内的可靠度,将时间段[0,Ts]分为n个长度相同的微小时段τ,τ=Ts/n。当微段τ足够小时,可假设在微小时段τ内构件抗力R和荷载横向分布系数m为常数值,假设该常数等于对应微小时段的中值。将活载随机过程SQ在时间微段τ内的峰值记为SQi,则在[0,Ts]时间段内,钢筋混凝土构件的失效概率[14]为
式中:SG为恒载效应;I为列车荷载冲击系数。
式(14)为相对于ti时段的串联可靠度问题,假定相互独立,采用Stevnson-Moses算法[16]求解。
3 算例分析
3.1 概述
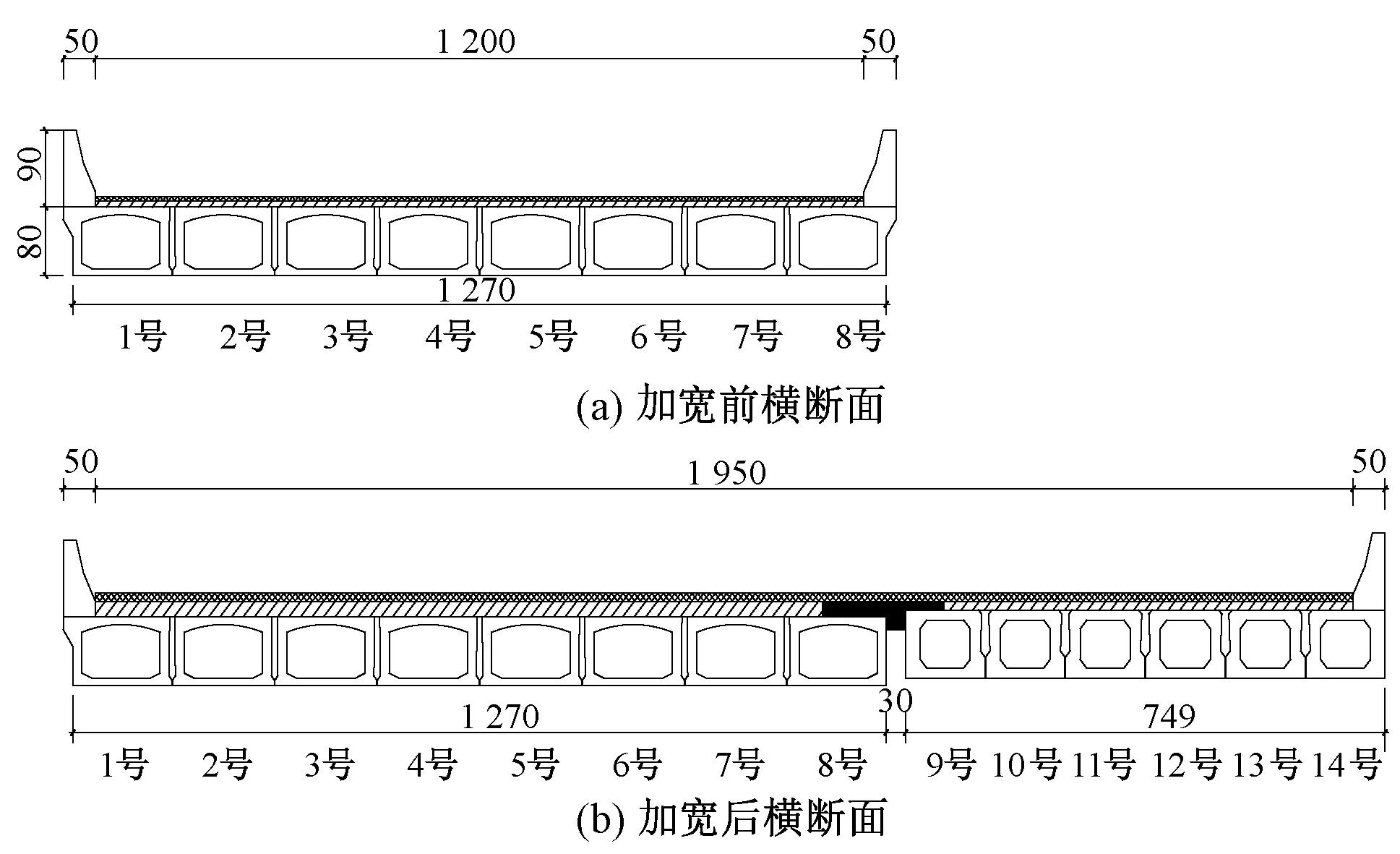
注:1号—8号为原桥主梁结构、9号—14号为加宽主梁结构图1 加宽前后横截面(单位:cm)
某钢筋混凝土简支板桥(如图1所示)采用装配式施工工艺,由8块钢筋混凝土预制空心梁板拼接而成,主跨全长16 m。原桥根据1989年颁布实施的JTJ 021—1989《公路桥涵设计通用规范》进行设计。汽车荷载等级:汽车超20级,挂120级,采用C30混凝土,构件保护层厚度30 mm,运营期已近20年。该桥加宽改造部分,采用C50级混凝土,后张法浇筑空心预制梁,预应力钢筋束保护层厚度根据规范设为 62 mm。该桥所处地区年温度统计平均值通常情况下为21.9 ℃,年相对湿度统计平均值通常情况下为77%。
3.2 承载能力劣化
图2(a)为旧桥中梁抗弯承载能力均值随时间变化。可以看到,运营期40年为旧桥承载能力变化的一个分界点,该点前变化幅度基本不大,承载能力基本完整,但是服役超过40年承载能力开始出现明显退化,呈现下降趋势。旧桥中梁承载能力均值在设计使用年限100年内由 2 234.9 kN·m 下降到 2 066.7 kN·m,其中在40~100年时间段下降最为明显,下降幅度为8.5%。图2(b)为旧桥中梁抗弯承载能力标准差,在服役前40年,承载能力标准差为 318.9 kN·m,一直保持不变,服役40年后,抗弯承载能力标准差逐渐增大,到服役期100年时,增长至 386.7 kN·m,增长幅度为21.3%。可见,钢筋发生锈蚀后中梁的抗弯承载能力均值明显下降而标准差显著上升。
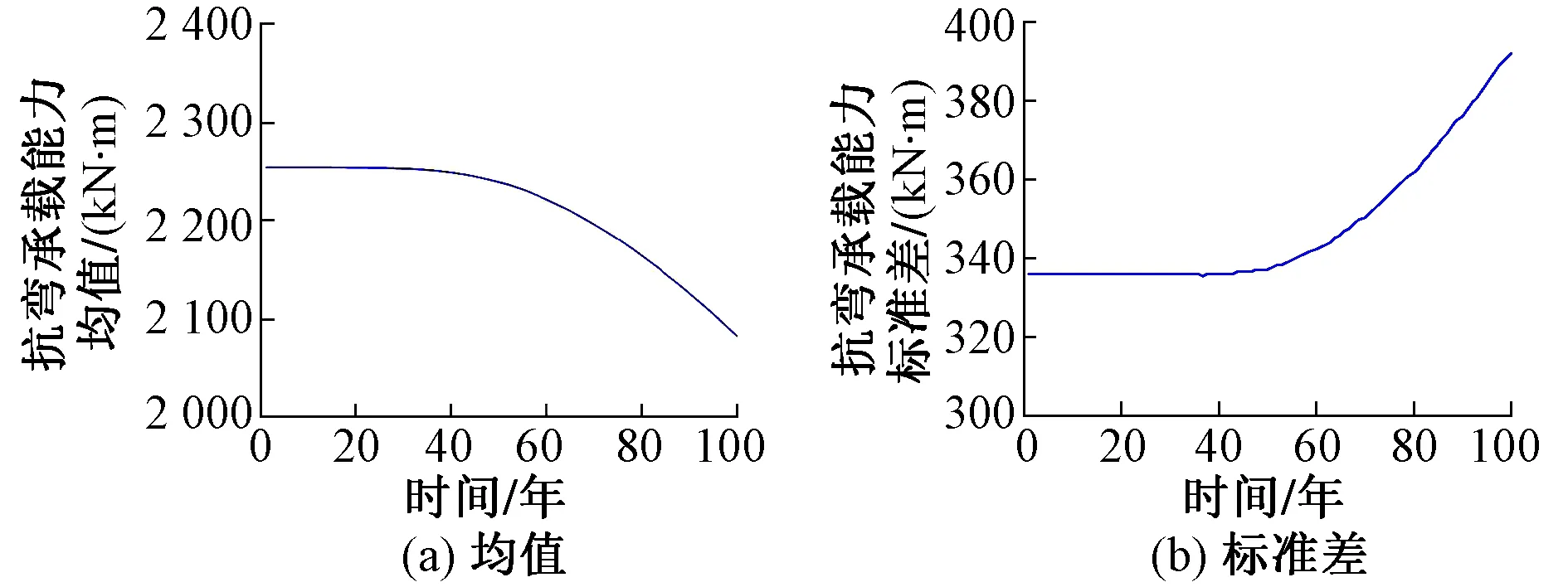
图2 旧桥中梁抗弯承载能力均值和标准差
3.3 加宽后刚度与横向分布系数变化
图3(a)中所示为不同梁号的主梁在加宽改造前后各主梁的横向分布系数变化趋势对比。可以看出,旧桥各梁均较改造前有所降低,其中距离新桥越近降低越明显。在劣化环境的作用下,混凝土碳化造成构件内部钢筋锈蚀,进而会引起梁开裂截面等效刚度发生变化,选择旧桥典型位置中梁的等效刚度进行统计,获得平均值如图3(b)所示。
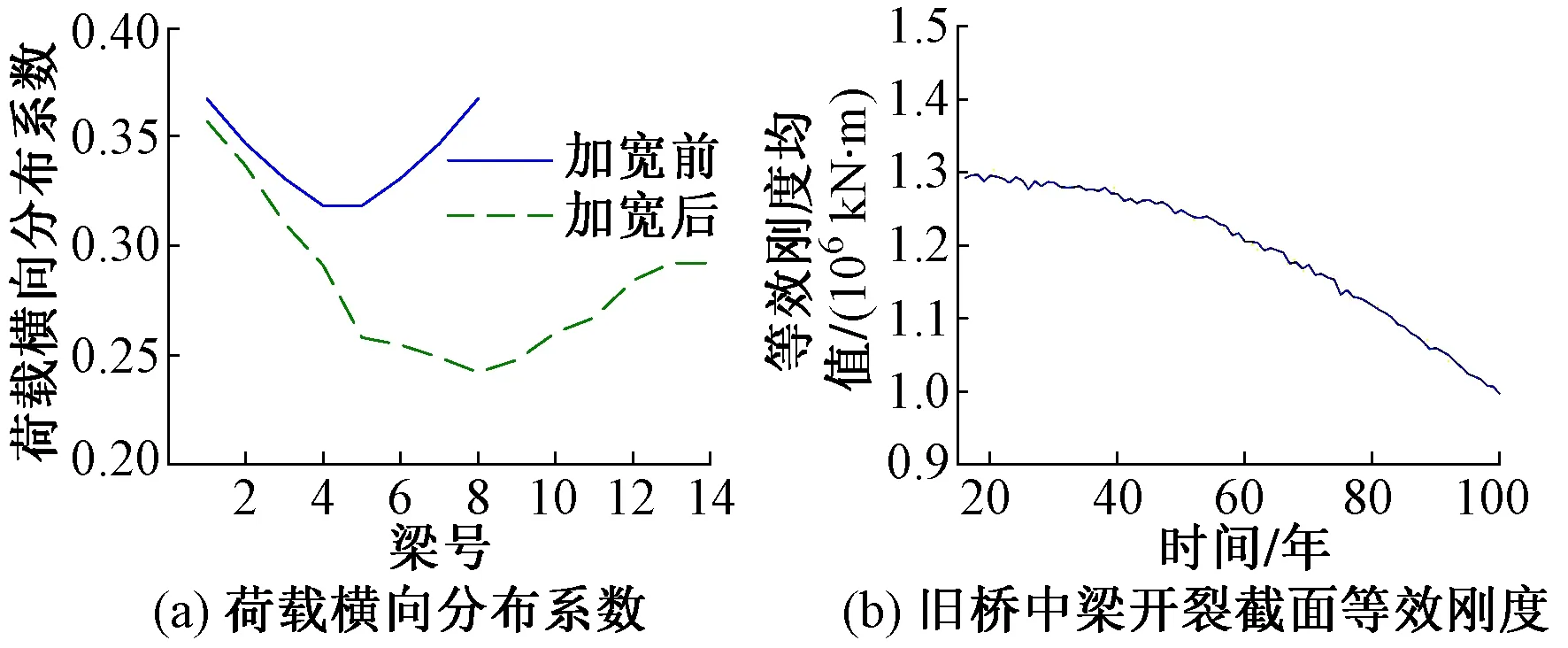
图3 主梁加宽改造横向分布系数和等效刚度均值变化
从图3(b)可以看出,运营期在25年内时,旧桥梁的刚度变化并不明显,一直维持在1.29×106kN·m左右,第40年旧桥截面等效刚度均值下降为1.27×106kN·m,之后等效刚度下降速度加快,当桥梁服役达到100年时,旧桥主梁等效刚度下降至0.99×106kN·m,下降幅度达23.2%。对比图2(a)与图3(b) 可以发现,在钢筋锈蚀作用下主梁等效刚度均值下降幅度大于承载能力均值下降的幅度。
旧桥5号、6号、7号及8号梁的荷载横向分布系数均值在刚拼接完成时,4根主梁横向分布系数均值分别为0.354,0.255,0.243和0.239;服役80年后,分别下降为0.336,0.237,0.226和0.219;服役100年后进一步下降为0.323,0.224,0.214和0.202,下降幅度分别为8.31%,10.80%,12.41%和15.81%。加宽改造后的9号、10号、11号及12号梁的横向分布系数均值分别为0.250,0.260,0.267,0.284;加宽后65年,分别上升为0.270,0.272,0.275和0.286;加宽后85年,上升为0.295,0.285,0.286和0.288,上升幅度分别为18.5%,9.2%,7.1%和1.4%。由此可见:旧桥等效刚度下降与旧桥横向分布系数升降呈现明显正相关,而新桥横向分布系数则呈现出相反的态势。
改造前旧桥5号、6号、7号、8号主梁的荷载横向分布系数变异系数均在0.131附近,随着旧桥在环境中发生劣化后,旧桥横向分布系数变异系数呈逐渐增大趋势,加宽改造65年后,分别上升到0.167,0.174,0.179,0.203,加宽改造85年后,进一步上升至0.211,0.222,0.236,0.299。
加宽改造后新桥的荷载横向分布系数的变异系数在劣化环境作用下必然会逐渐增大,当主梁服役在40年以内时,变异系数变化并不明显时,各主梁均保持于0.129附近,随着旧桥服役超过40年,加宽部分变异系数均明显上升,新桥横向分布系数的变异系数变化趋势基本与旧桥变化一致,加宽后65年分别上升到0.200,0.156,0.147,0.131;加宽后85年进一步上升为0.288,0.187,0.173,0.136。
3.4 时变可靠度指标
选取加宽后旧桥典型位置1号梁和8号梁,在3种不同工况下,考虑加宽时旧桥1号和8号梁的可靠度指标明显高于未加宽时。以1号梁为例,服役100年时考虑加宽工况下刚度不同步劣化的工况为3.18,而不考虑加宽工况下为3.13,提高了0.05。加宽后是否考虑刚度劣化不同步问题也影响可靠度指标的准确获取。对1号梁和8号梁对比分析发现,旧桥加宽前后的可靠度指标增幅明显不同,8号梁增幅明显高于1号梁,进一步分析发现,2号至7号梁增幅明显存在上升趋势,并在1号和8号梁之间,因此可以得出:加宽可以提高旧桥各主梁时变可靠度指标,其中距新旧桥拼接缝距离越近提高幅度越大。
图4为新桥典型位置梁可靠度指标。考虑新、旧桥刚度不同步劣化影响后,9号梁的时变可靠度指标由8.25下降到6.31,下降幅度为23.5%;14号梁的时变可靠度由8.27下降到8.24,下降幅度为3.6%。进一步研究发现:10号至13号梁时变可靠度指标下降幅度介于9号与14号梁之间,且依次减小。当新、旧桥刚度发生不同步劣化后,旧桥主梁的时变可靠度指标小幅上升,上升幅度小于新桥下降的幅度,这是因为旧桥的横向分布系数均值下降造成旧桥时变可靠度指标略有增加,但同时旧桥横向分布系数标准差上升会造成旧桥时变可靠度指标下降,两者效应有所抵消,而对新桥,其横向分布系数的均值和标准差均上升,两者均引起新桥主梁可靠度指标下降且两者效应叠加。
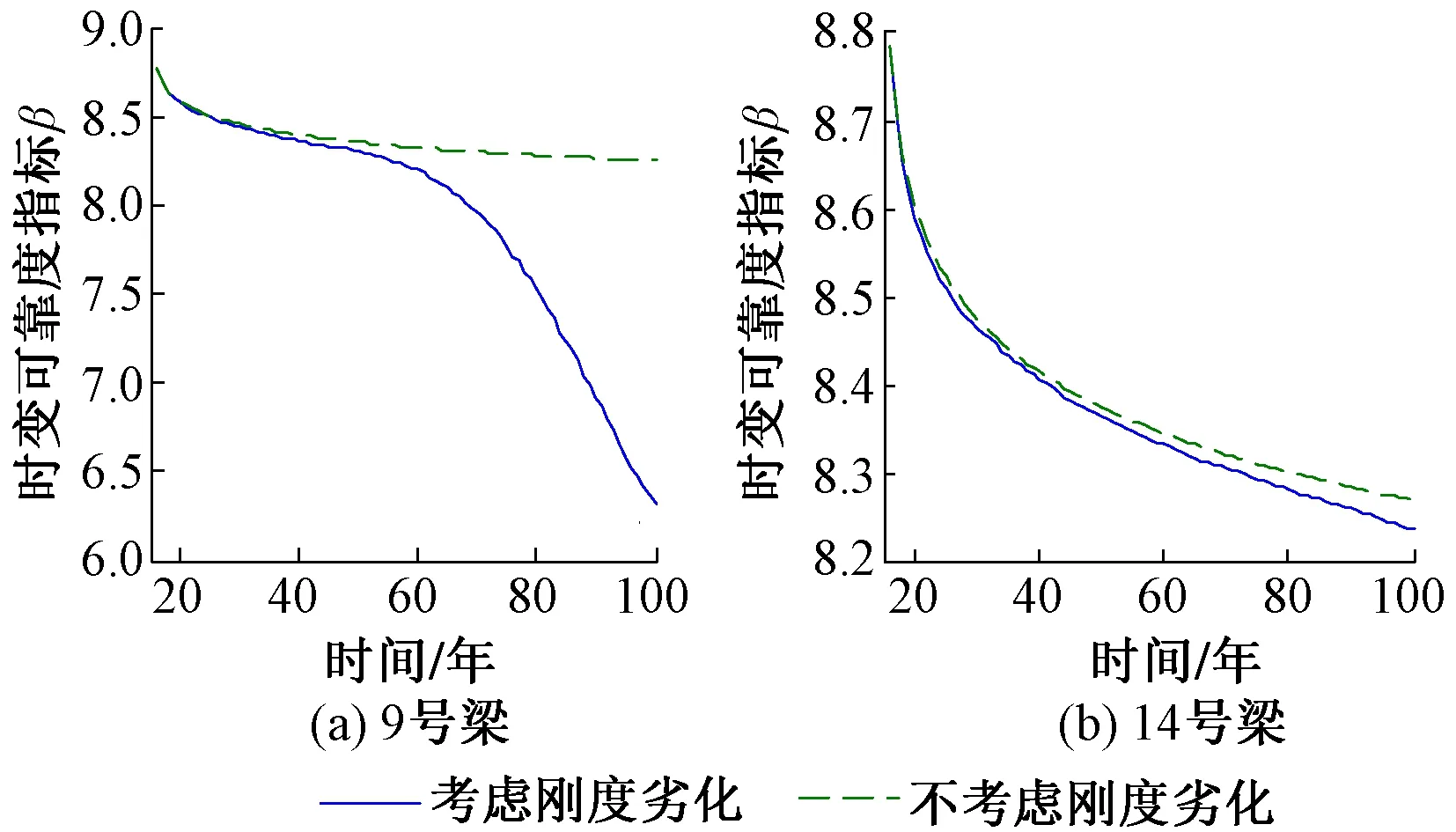
图4 新桥典型位置梁可靠度指标
4 结论
1)加宽改造有效减小了原桥各主梁的横向分布系数,在新旧桥拼接缝附近减小幅度最大,同时原桥的时变可靠度也有所提高,提高幅度与距拼接缝距离具有密切关系。
2)加宽后新旧桥性能劣化并不同步,既有桥梁的劣化要先于新桥且劣化程度比新桥严重。新、旧桥的不同步劣化引起原桥荷载横向分布系数的均值降低,标准差上升,进而引起新桥荷载横向分布系数均值和标准差均增大。
3)加宽改造后由于刚度劣化不同步影响,旧桥的时变可靠度升高的幅度小于新桥的降低幅度。
