索梁结构应急桥抖振响应分析

杨 磊，邵 飞，徐 倩，胡玉博

(1.陆军工程大学 野战工程学院，江苏 南京 210007；2.空军勤务学院 勤务保障系，江苏 徐州 221000)

抖振是桥梁在大气紊流风作用下的响应，是一种不可避免的随机强迫振动，且抖振响应影响行车的舒适性。近年来，在桥梁风工程研究方面大量学者采用时域分析法研究了桥梁结构的抖振响应[1-3]。Davenport在1960年提出了随机抖振响应分析理论，并提出大气紊流脉动风谱形式。这一理论依然是目前研究结构抖振问题的主要方法。Tao等[4]对大跨度三塔悬索桥进行抖振参数分析，结果表明选择适当的脉动风功率谱和气动导纳函数对桥梁结构的抖振响应计算非常重要。Huang等[5]对施工阶段悬索桥进行颤抖振时域分析，考虑不同流场非线性因素的影响。刘孝辉等[6]基于Davenport准定常分析方法和风洞试验，研究大跨度公轨两用钢桁梁悬索桥的抖振响应，分析了钢桁梁悬索桥抖振响应特性。李飞等[7]采用时域抖振分析法研究了大跨度预应力混凝土连续刚构桥的抖振响应，发现主梁风致响应与桥梁结构体系的变化直接相关。陈代海等[8]基于模拟的脉动风场和桥梁结构抖振分析基本理论，采用ANSYS软件编制程序分析大跨度窄桥面钢桁架悬索桥抖振响应，并分析了气动导纳函数和气动自激力对该桥梁结构抖振响应的影响。众多学者主要研究大跨度斜拉桥、悬索桥、拱桥的抖振响应[9-11]，而对轻质应急桥结构抖振响应未见研究。

索梁结构应急桥与其他大型民用公路桥梁相比刚度小、质量轻，且主梁连接采用铰接，这些因素会使桥梁结构在风荷载作用下产生振动。应急工程保障地区往往地形复杂，风场波动性较大，因此有必要对索梁结构应急桥的抖振响应进行研究。本文以索梁结构应急桥为研究对象，运用谐波合成法模拟生成脉动风，采用抖振力时域表达式和脉动风计算桥梁结构所承受的抖振力时程。基于ANSYS软件编制抖振响应分析程序对成桥状态索梁结构应急桥进行抖振时域响应分析。

1 索梁结构应急桥及风场模拟

1.1 索梁结构应急桥

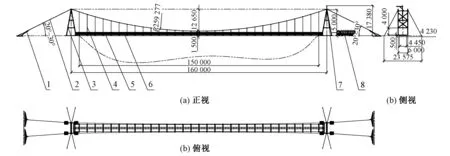
1-锚碇系统;2-主索;3-塔架总成;4-吊具总成;5-桥面总成;6-安全网;7-架设设备及工具;8-运输车系统图1 新型索梁结构应急桥总体布置(单位：mm)

新型索梁结构应急桥主要由缆索系统、主梁、塔架和锚碇系统组成，总体布置如图1所示。桥梁跨径150 m，塔高15 m，主缆垂跨比1/11.86，加劲梁梁高0.75 m。缆索系统包括主缆和吊杆，全桥共设置2根主缆，材料为高强纤维绳，拟用SPECTRA纤维绳。主缆采用骑跨式，横桥向间距为6 m。在桥跨上布置吊杆并锚固于主横梁上，顺桥向间距为10 m，共30根，材料为圆钢。塔架为桁架式，材料为铝合金7005，主要由塔架主梁柱和塔架次梁柱拼装组成，截面均为H形铝合金型材，总高15 m。主梁分为标准梁、边梁和主横梁3部分。桥面总成见图2。标准梁截面为组合板梁结构，见图3(a)；主横梁采用工字形断面，见图3(b)。

1-固定支座;2-边梁;3-主横梁;4-标准梁;5-中间填板;6-梁插销;7-吊杆插销;8-滑动支座图2 桥面总成(单位：mm)

图3 典型断面(单位：mm)

1.2 桥梁结构动力特性

采用ANSYS软件建立全桥空间有限元模型，标准梁与主横梁均采用Beam 4三维梁单元模拟。因填板是挂靠在加劲梁上以保证一定的安全性，故不考虑两加劲梁间填板对桥梁结构刚度的贡献，将其质量和转动惯量集中至横梁上，采用Mass 21单元模拟；塔架构件有多种截面，采用Beam 188单元模拟；主缆及吊杆采用Link 10单元模拟，主缆和吊杆的初应力以初应变的方式施加。主梁与桥塔均采用约束节点自由度的方式模拟边界条件。主梁在梁端均为纵向滑动支座，故仅约束其竖向与横桥向平动自由度；桥塔底部与主缆锚固点均约束竖向、纵桥向与横桥向平动自由度。加劲梁与主横梁采用单双耳插销连接，为准确模拟其连接特性，在纵梁与横梁上建立相应数量的刚臂单元至连接位置处后耦合刚臂节点自由度，再释放横桥向转动自由度。应急桥动力特性计算结果见表1。

表1 应急桥动力特性计算结果

1.3 风场模拟

风速中包含平均风分量和脉动风分量，紊流中各频率贡献的大小可表示为脉动风分量的功率谱函数。空间脉动风速由3个方向的脉动风速构成，不同方向的脉动风速有不同的风速谱函数。对于长宽比较大的桥梁结构而言，一般只考虑顺风向风谱和竖向风谱。基于JTG/T 3360-01—2018《公路桥梁抗风设计规范》[12]，水平脉动风谱采用高度变化的Kaimal谱，竖向脉动风谱采用Panofsky谱。索梁结构应急桥架设场地的地表类别为B类，场地10 m高处10 min平均100年重现期设计风速取27.5 m/s。参考JTG/T 3360-01—2018，其风廓线指数为0.16，粗糙高度为0.05 m。风场模拟截止频率为20π Hz，频率点个数为 2 048，时间步长为0.1 s，采样时间总长为600 s。使用Matlab软件编制脉动风模拟程序。

模拟点分布见图4。模拟主梁跨中脉动风速时程曲线，见图5。本文从功率谱、相干函数方面对该风速时程曲线进行验证。通过对程序生成的脉动风进行处理，可得应急桥横桥向和竖桥向的风速功率谱和自相关函数，分别见图6和图7。可见，横桥向、竖桥向脉动风速功率谱的模拟值与目标值吻合较好；横桥向、竖桥向相关函数模拟值与目标值吻合较好；脉动风速模拟结果满足要求，可用于应急桥的抖振响应分析。

图4 模拟点分布

图5 主梁跨中脉动风速时程曲线

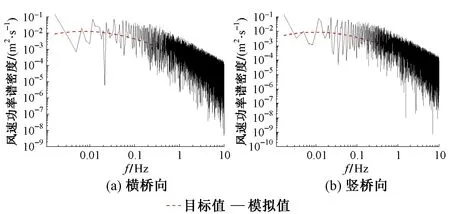
图6 主梁跨中脉动风速功率谱

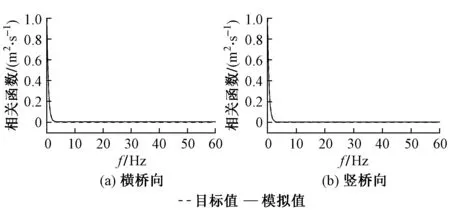
图7 主梁跨中自相关函数

2 索梁结构应急桥抖振分析

Davenport准定常抖振理论和Scanlan抖振理论为桥梁结构抖振响应分析的两大经典理论。对索梁结构应急桥抖振响应分析时采用Davenport准定常抖振计算公式。根据模拟的脉动风编制抖振程序，计算分析气动自激力和气动导纳函数对桥梁结构抖振响应的影响。对桥梁结构进行抖振力加载时，应考虑来流风攻角α和主梁单元的扭转角β，将α+β作为有效风攻角并提取相应的三分力系数计算风荷载。抖振力分解如图8所示。在同济大学风洞实验室对主梁节段模型做风洞试验，得到应急桥主梁风轴坐标系下三分力系数，见图9。

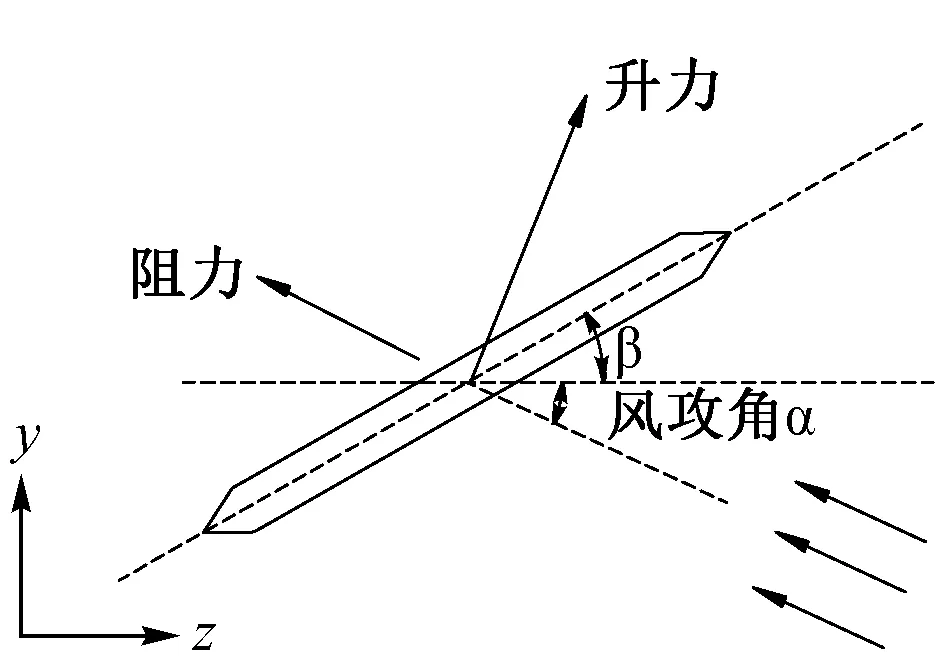
图8 抖振力分解

图9 主梁风轴坐标系下三分力系数

计算桥梁结构抖振响应时，首先考虑静风荷载作用下桥梁结构的平衡位置，然后在每一个计算子步中读取模拟得到的脉动风和试验测得的三分力系数。计算子步抖振力，并将其加载到应急桥主梁和塔架节点上进行抖振响应计算。基于ANSYS内置语言APDL编制索梁结构应急桥非线性时域抖振分析程序。

本文计算索梁结构应急桥抖振响应时对主缆和塔架只考虑阻力的影响；综合考虑静风荷载和抖振荷载，忽略气动自激力的影响；气动导纳函数取1，即忽略气动导纳函数的影响。采用抖振分析程序对索梁结构应急桥进行抖振分析，应急桥关键节点抖振响应计算结果见表2。其中，RMS (Root Mean Square)表示应急桥结构响应的均方根值。可知：成桥状态下索梁结构应急桥抖振横向位移远大于竖向位移；跨中位置横向位移峰值达到 0.629 0 m，1/4跨横向位移达到 0.444 9 m，桥梁结构横向位移比较突出。说明桥梁结构侧向刚度较小，侧向稳定性差，须采取合理的结构措施进行控制。

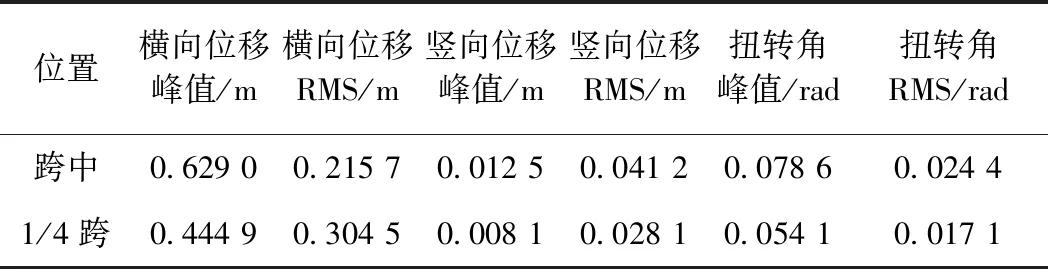
表2 应急桥关键节点抖振响应计算结果

通过抖振时域程序计算得到应急桥跨中抖振响应时程曲线，见图10。跨中抖振位移及扭转角RMS沿顺桥向变化曲线见图11。由图10可知，应急桥跨中的扭转角和竖向位移较小，横向位移相对较大，但横向加速度峰值小于竖向加速度峰值，说明桥梁结构受风阻力作用明显。由于桥梁结构为组合板梁断面，且采用轻质高强材料，主梁之间拼接连接，导致桥梁结构侧向刚度较小，应采用抗风缆等措施。由图11 可知，横向位移RMS峰值约为0.3 m，而竖向位移RMS约为 0.042 5 m，扭转角RMS峰值约为 0.025 rad，说明应急桥在脉动风作用下主梁跨中位置横向位移较大。

主缆及吊杆应力时程曲线见图12。可知，由于主缆采用轻质高强纤维缆材料，在自重和结构振动影响下，风速对跨中主缆应力幅值影响较大，幅值范围为160～250 MPa，在静风荷载和脉动风荷载共同作用下主缆轴向应力变化强烈。在重力和结构振动影响下，风速对跨中和1/4跨吊杆应力影响较小，吊杆应力最大值与最小值相差约5 MPa，跨中吊杆应力在12.0～17.5 MPa，而1/4跨吊杆应力在11.5～16.5 MPa，跨中吊杆应力幅值变化较1/4跨吊杆幅值略大。

图10 跨中抖振响应时程曲线

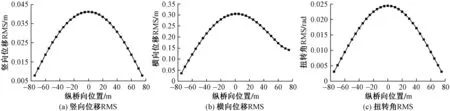
图11 跨中抖振位移及扭转角RMS沿纵桥向变化曲线

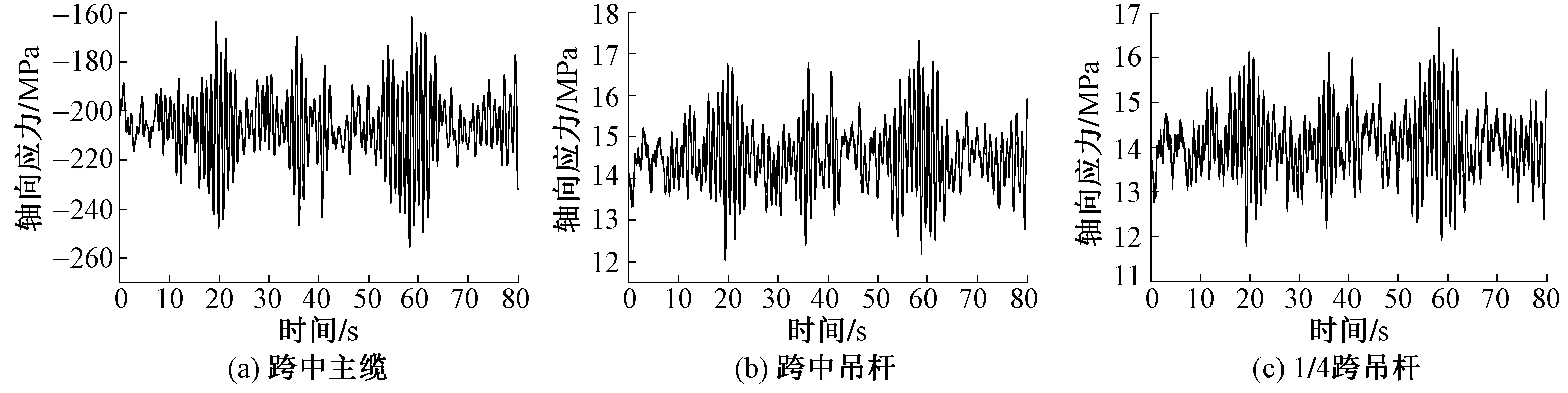
图12 主缆及吊杆应力时程曲线

在ANSYS结果中提取索梁结构应急桥跨中的抖振位移结果，对其做快速傅里叶变换可以得到在频域范围内桥梁结构的抖振响应，见图13。由图13(a)可知，与应急桥动力特性计算结果对比，跨中竖向位移功率谱主要受一阶竖弯振型的影响，卓越频率与一阶竖弯频率一致；由图13(b)可知，跨中横向位移主要受一阶侧弯振型的影响，卓越频率为0.62 Hz；由图13(c)可知，跨中扭转角主要受一阶扭转振型的影响。因此，索梁结构应急桥跨中抖振横向位移主要受主梁正对称侧弯振型的影响；抖振竖向位移主要受主梁一阶正对称竖弯振型影响；扭转角主要受主梁一阶正对称扭转振型影响。

图13 跨中抖振位移及扭转角功率谱

3 索梁结构应急桥抖振影响因素分析

3.1 气动导纳函数

索梁结构应急桥抖振分析基于准定常假定抖振力模型，与结构真实受力可能存在差别。通过气动导纳函数对准定常抖振力模型进行修正，可以准确模拟桥梁结构所受抖振力的非定常特性。考虑气动导纳函数时应急桥抖振位移响应RMS沿顺桥向变化曲线见图14。可知，考虑气动导纳函数后结构抖振位移响应会有不同程度的减小，横向位移、竖向位移及扭转角的RMS峰值分别减小了15.3%，16.5%，14.7%，说明不考虑气动导纳函数时索梁结构应急桥抖振响应偏于保守，但提高了桥梁结构的安全性。

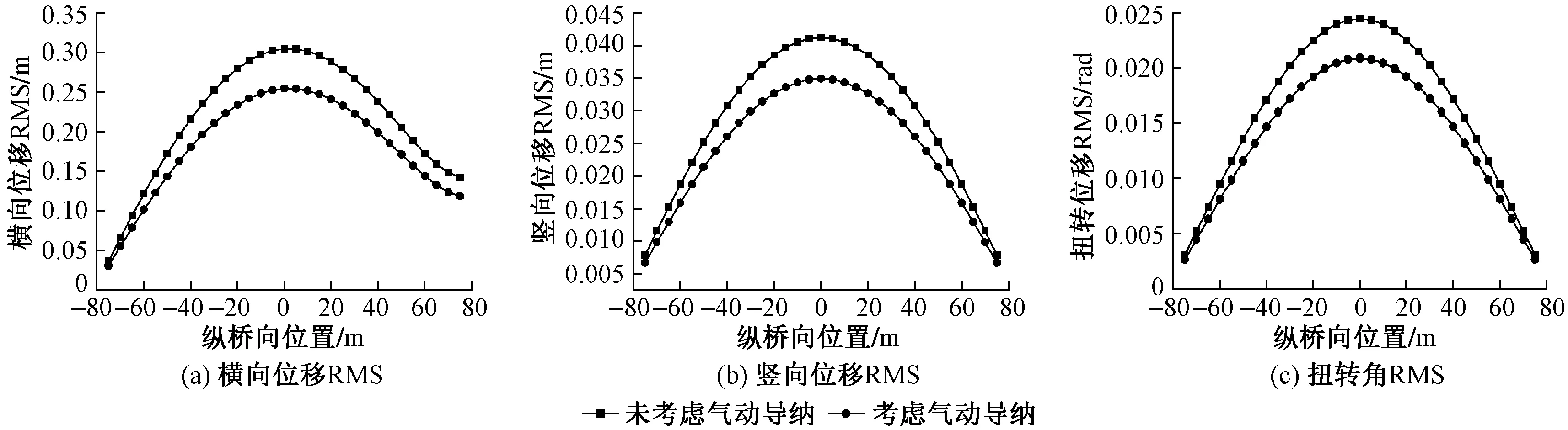
图14 考虑气动导纳函数时应急桥抖振响应RMS沿纵桥向变化曲线

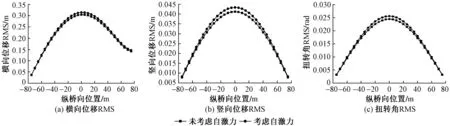
图15 考虑气动自激力时抖振响应RMS沿纵桥向变化曲线

3.2 气动自激力

采用Matrix 27单元模拟气动阻尼矩阵和气动刚度矩阵，从而模拟主梁上气动自激力的作用。考虑气动自激力时抖振响应RMS沿顺桥向变化曲线见图15。可知，考虑自激气动力后桥梁结构横向位移、竖向位移、扭转角RMS均有小幅增加，但影响不大，其中竖向位移RMS峰值增幅最大，达到5.3%。原因是在桥梁结构抖振响应中气动自激力表现出气动负阻尼的作用，一定程度上增大了结构位移响应。因此，在分析抖振响应时忽略自激力的影响会导致分析结果偏小。对于本文应急桥结构，考虑气动自激力与否对于应急桥抖振位移影响较小。原因是应急桥桥跨结构刚度小、质量轻，产生的气动自激力太小，对新型应急桥结构抖振响应影响较小。

4 抗风缆对应急桥方案抖振响应的影响

为提高桥梁结构安全性，在原应急桥方案上增加水平抗风缆，在新型索梁结构应急桥L/4，L/8，3L/16 处对称设置水平抗风缆，抗风缆初应变均为0.003，抗风缆锚固于两岸。对提出的抗风缆方案进行抖振计算分析，考虑抗风缆时应急桥抖振位移RMS沿顺桥向变化曲线见图16。可知：抗风缆能很好地控制横向位移，而对竖向位移和扭转角影响较小；跨中横向位移较原方案减小了45.1%。

图16 考虑抗风缆时应急桥抖振响应RMS沿纵桥向变化曲线

5 结论

本文对索梁结构应急桥在脉动风荷载作用下的抖振响应进行了计算分析，研究了气动导纳函数和气动自激力对索梁结构应急桥抖振响应的影响。通过分析可得如下结论：

1)索梁结构应急桥抖振横向位移远大于竖向位移及扭转位移，说明桥梁结构侧向刚度较小，侧向稳定性差。

2)由于主缆采用轻质高强纤维缆材料，风速对跨中主缆应力幅值影响较大，而吊杆应力变化幅值较小，因此在静风荷载和脉动风荷载共同作用下主缆轴向应力变化强烈，吊杆相对稳定。

3)索梁结构应急桥跨中横向位移主要以主梁正对称侧弯振型为主；竖向位移主要以主梁一阶正对称竖弯振型为主；扭转角主要以主梁一阶正对称扭转振型贡献为主。

4)不考虑气动导纳函数，索梁结构应急桥抖振响应计算结果相对保守，不考虑气动自激力对桥梁结构抖振响应计算结果影响较小。与气动导纳函数对抖振响应结果的影响相比，气动自激力影响较小，从计算便捷性方面考虑可以忽略。

5)斜拉索抗风缆方案能够极大降低应急桥横向位移，但对竖向位移和扭转角的影响较小。