对《突出基本结构落实核心素养》一文的补充
2019-08-07陕西省西安建筑科技大学附属中学710055刘志勇
陕西省西安建筑科技大学附属中学(710055) 刘志勇
本刊2018年第12 期(下)第17 页刊文《突出基本结构落实核心素养—一道平面几何试题的教学和反思》,就一道平面几何试题的教学进行了研究,引导学生从复杂的图形中分离出基本几何结构,从而构造与问题相关的方程模型进行求解,进而落实数学抽象、逻辑推理、数学建模、直观想象、数学运算等数学核心素养的培养,下面笔者将对该文做一些补充.
一、原题
如图1,在△ABC中,∠BAC=45°,AD⊥BC于D,若BD=3,CD=2,则AD=____.
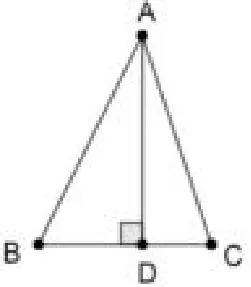
图1
二、补充思路
思路一如图2,由AD是△ABC的高想到作另外两条高,利用”三角形三条高交于一点”.
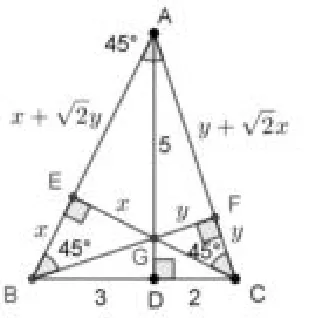
图2
1.由勾股定理,得BG2-BD2=CG2-CD2,即2x2-32=2y2-22,即x2-y2=,再由BE2+EC2=BC2得x2+(x+联立 ① ②,解得x2=5 或(舍),所 以x2=5.所 以GD=再由可得AG=BC=5.所以AD=AG+GD=5+1=6.
2.设GD=m,由△BDG∽△AFG可得即即由△AEG可得即即②,①②得:即解得m=1 或-6 (舍),所以m=1.再由可得AG=BC=5.所以AD=AG+GD=5+m=5+1=6.
思路二如图3,由∠BAC=45°想到圆周角,于是作△ABC的外接圆,圆心为O.
1.如图3,可推出DE=2,EF=1.再可推出△ABF∽△CAE,于是即解得AD=6或-1(舍),所以AD=6.
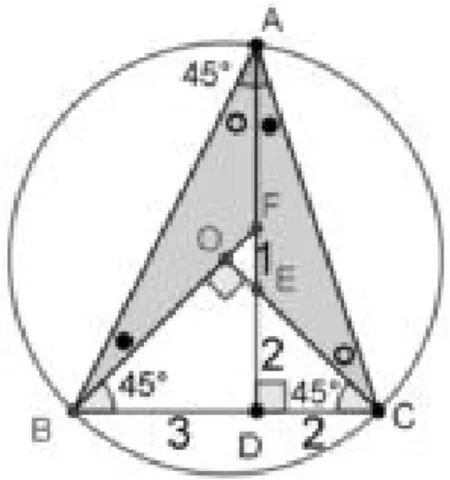
图3
2.如图4,作OE⊥BC于E,OF⊥AD于F,连接AO.可推出DF=EO=BE=OF√=ED=半径AO=BO=在Rt△AOF中,由勾股定理,得AF所以AD=AF+DF==6.
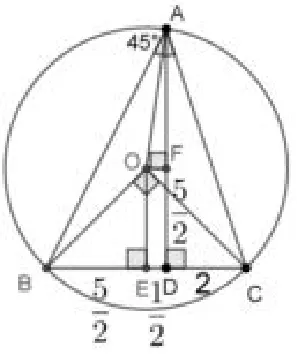
图4
思路三如图5,由于AD将∠BAC=45°分为∠BAD和∠CAD,这两个角的和为45°,它们的2 倍为90°,于是想到将这两个角分别2 倍,也就想到轴对称.
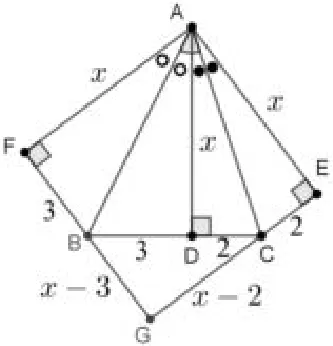
图5
分别作AD关于AC和AB的对称图形AE,AF,FB与EC交于点G,可得正方形AEGF.设AD=x,则BG=x-3,CG=x-2,在Rt△BCG中,由勾股定理,得(x-3)2+(x-2)2=52,即x2-5x-6=0,解得x=6 或-1 (舍),所以x=6,即AD=6.
思路四如图6,由∠BAC=45°想到tan∠BAC=tan 45°=1,想到直线y=x.
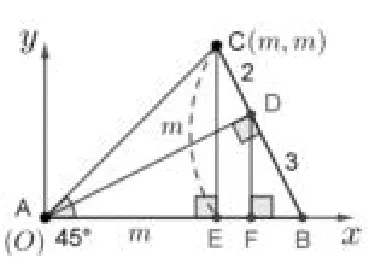
图6
将△ABC放到平面直角坐标系中,使A在原点,AB在x轴正半轴上,点C在第一象限.显然直线AC的解析式为y=x.设直线AD的解析式为y=kx(k /=0),C点坐标为(m,m),由AD⊥BC,则可设直线BC的解析式为y=(x-m)+m,联 立可求出D点坐标为作CE⊥AB于点E,DF⊥AB于点F.再由△BDF∽△BCE可得DF=m,即又因为所以即解得k=或-3(舍),所以k=所以tan∠DAB=k=所以推出AD=6.
思路五如图7,受上一个思路的启发,去掉坐标系的背景,用三角函数解决问题.由CE=AE,可设AE=CE=5m,由DF//CE,CD=2,BD=3,可设EF=2n,BF=3n,推出DF=3m.因为∠DAF=∠BDF,所以tan∠DAF=tan∠BDF,所以即即2-3=0,解得或-3(舍),所以所以tan∠DAF=tan∠BDF=又因为tan∠DAF=所以所以AD=6.
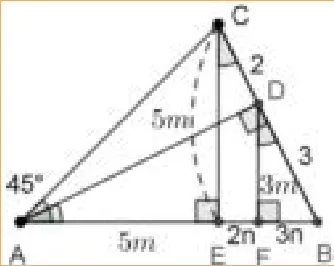
图7
思路六如图8,可以看出∠α+∠β=45°,而tan∠α=tan∠β=因此想到如果能找到tan∠α和tan∠β满足的关系式,就能求出AD的值.

图8
1.构造图形,如图9,∠α+∠β=45°,则有tan∠β=所以tan∠α+所以tan∠α+tan∠β+tan∠α×tan∠β=即:若∠α+∠β=45°,则tan∠α+tan∠β+tan∠α ×tan∠β=1.代入tan∠α和tan∠β的值,可得即AD2-5AD-6=0,解得AD=6 或-1(舍),所以AD=6.

图9
2.构造图形,如图10,∠α+∠β=45°,设FG=EG=a,HF=b,则EF=由△EF√H∽△KFE可得可得KF所以所以tan∠α+tan∠β+tan∠α×tan(∠β=同上1 可得,AD=6.
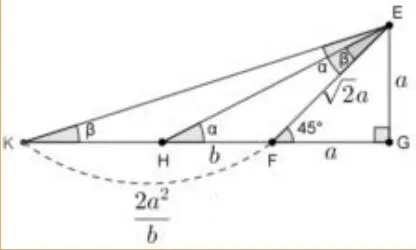
图10
