丁坝群对弯道水力特性影响的数值模拟研究

魏文礼， 陈晓朋， 李 强， 张泽伟， 刘玉玲

(西安理工大学 西北旱区生态水利国家重点实验室， 陕西 西安 710048)

1 研究背景

河床演变及水中泥沙运动由河流水流特性所决定，水流流经弯道时所形成的螺旋流会对许多工程造成破坏，为维护岸坡稳定，改善弯道内的水流流态，需在弯道内布设丁坝。为此，许多学者对弯道水流特性以及在弯道内布设丁坝后的水流流态进行了研究。王青等[1]采用数值模拟的方法，对陡坡弯道段的急流进行了研究，通过物理模型试验数据的验证，验证了数值模拟结果的正确性。通过计算结果，分析了陡坡弯道对急流流态的影响，提出了导流墙法的弯道急流优化方案，通过物理模型进一步证明，采用导流墙法可有效改善急流弯道水流流态。杨程[2]、Zhu Chuanjie等[3]对分别对90°、120°、150°弯道内的水流进行了研究，研究表明：凸岸区域的纵向流速小于凹岸，凹岸水位高于凸岸，最大流速区逐渐向弯顶断面转移，其设定条件下渠弯的最合理角度为150°。此时凹岸冲刷最小。Mazhar等[4]采用试验的方法对单、双S型弯道内的流场结构和流速分布规律进行了研究，得出：水流流过第1个S型弯道后弯道螺旋流已充分发展，对于单S型弯道和双S型弯道的第1个S型弯道，流速沿凸岸不断增加，当水流经过弯道后高流速区由凸岸向凹岸转移。与单S型弯道相比，双S型弯道的最大流速区靠近凹岸。白玉川等[5]对U型弯道进行了试验研究，研究表明：与垂向流速的变化相比，横向、纵向流速的变化更为明显。在沿水深及沿纵向上紊动能变化均较大，弯道底部紊动能最大，沿流向紊动能的最大值从左岸到右岸，再从右岸到左岸不断变化，最后基本保持不变。吴华莉等[6]、魏文礼等[7-8]对复式断面弯道进行了数值模拟研究，得出：纵向流速从凸岸到凹岸逐渐减小，主槽流速小于滩地流速，在弯道处矩形断面，明渠水流的横向流速大于复式断面明渠，而横比降及压强差小于复式断面明渠。Mohammad等[9]、Duan等[10]应用SSIIM模型对90°弯道内布设T型丁坝后丁坝之间的间距进行了研究，研究表明：在弯道的不同位置布设淹没和非淹没丁坝时，形成的冲刷坑形式有较大的区别。在不同工况下，二次流强度最大的位置发生在第一座丁坝上游区域，而最大沉积坑发生在凸岸出口附近的区域。两座T型丁坝之间的间距不应大于丁坝长度的5倍。与非淹没丁坝相比，淹没丁坝的最大冲刷坑深度减小了22%，沉积发生的位置离弯道出口也较远。苏伟等[11]、杨静等[12]对水流流经不同形式丁坝的紊动特性，丁坝附近的冲刷程度分别进行了试验研究，得出：紊动动能及紊动强度可以反映水流紊动对丁坝附近的冲刷情况，河床中的细砂一部分在主流作用下被冲走，另一部分在回流区发生沉积，粗砂受过坝水流作用，在下游河床形成沙垄，冲刷坑只形成于沙垄右侧。以往的研究都是单纯研究弯道或丁坝水流，对60°弯道内布设丁坝群后的水流特性研究较少，本文采用数值模拟的方法对60°弯道内布设3座丁坝后的流速分布、流场结构和水面形态进行研究，并将模拟结果与文献[13]中的资料进行了比较。得出丁坝群在维护河岸稳定及改善航道方面有较好的效果，对工程实践具有参考价值。

2 数学模型与计算方法

描述水流的质量守恒和动量守恒方程以及RNGk-ε紊流模型的方程如下[14]。

质量守恒方程：

(1)

动量守恒方程：

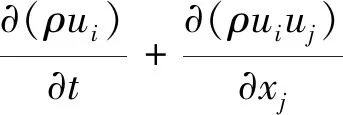
(2)

(3)

紊流动能k和紊动能耗散率ε的方程：

(4)

(5)

式中系数及表达式：

式中：Cμ=0.0845为经验常数；σk为与湍动能k(m2/s2)对应的Prandtl数；σε为耗散率ε(%)对应的Prandtl数，Sij为平均应变率，%。

自由水面由网格单元中流体和网格体积比函数[15]Fw(t,xi)来确定。描述Fw的控制方程为：

(6)

引入VOF后，ρ、μ为Fw(t,xi)的函数，其表示式为：

ρ=Fwρw+(1-Fw)ρa

(7)

μ=Fwμw+(1-Fw)μa

(8)

式中：ρw和ρa分别为水和空气的密度，kg/m3；μw和μa分别为水和空气的分子黏性系数，N·S/m2。

将上述方程与紊流数学模型基本方程施加相应的边界条件后，就可得到相应各未知变量，如流速、紊动动能、以及紊动耗散率等的分布。

丁坝对河道水流流态的改善方面具有良好作用，本文将丁坝群布置在具有螺旋流的弯道内，以60°弯道为例，采用RNGk-ε湍流模型，模拟凹岸布设不同间距的3座丁坝群前后的水流特性，比较模拟值与实验值，发现两者拟合效果良好。

3 物理模型与边界条件

3.1 计算区域与网格

如图1所示，本文的模型验证采用文献[13]中的模型，弯道中心角为60°，过水断面为矩形，宽0.6 m，高0.4 m，弯道底宽与弯道中心线曲率半径之比为0.4，进口和出口分别设有2 m直段以平顺水流。丁坝长L=0.16 m，宽B=0.02m，高H=0.45 m，3座丁坝从弯道入口依次布置，第1座丁坝、第2座丁坝、第3座丁坝距弯道入口分别为1.8L、4.8L、6.8L。入口流量为53 L/s，初始水深0.24 m。

如图2为弯道内各测速点的布置图，在径向上每4°设一监测断面，监测断面总共布设有16个。

3.2 边界条件

弯道进口边界设为速度进口，速度为0.351m/s，出口边界设为压力出口，弯道顶面设为压力出口，相对压强为0。弯道壁面和丁坝均采用无滑移边界条件，所有壁面都采用标准壁面函数进行处理，模型的离散采用有限体积法，采用VOF法捕捉自由水面。

图1 计算区域图

计算网格如图3所示，对丁坝附近局部区域的网格进行加密，网格总数为213 500，时间步长设为0.001 s，计算到速度监测值不再变化为止。

图2 平面监测断面布置图

图3 物理域计算网格图

4 结果分析与讨论

4.1 模型验证

本文将无丁坝及布设丁坝后的流速与水位的模拟值，与周阳[13]在水槽中进行的模型试验结果进行比较，验证所选数学模型的可靠性。

4.1.1 流速 如图4所示为纵轴线上水位为0.2 m时，有、无丁坝情况下不同监测断面流速模拟值与试验值的比较。从图4可以看出，布设丁坝前后弯道纵轴线上流速有明显不同，无丁坝时弯道内最大流速的模拟值和试验值分别为0.363、0.364 m/s，相对误差为0.27%；有丁坝时弯道内最大流速的模拟值和试验值分为0.524、0.529 m/s，相对误差为0.95%。模拟得到的流速值总体上略低于实验值但误差较小，模拟值与实验值的最大相对误差为2.86%，模拟值与实验值吻合较好。

4.1.2 水位 图5为有、无丁坝情况下纵轴线上不同监测断面水位的模拟与试验值的比较，布置前水位最大相对误差为3.2%，布置后水位后第1座丁坝前壅水高度的模拟值和试验值分别为0.253、0.251 m，相对误差为0.8%。总之，所选用的数学模型能够较准确地模拟60°弯道内的水流特性。

4.2 速度分析

为研究60°弯道内布设丁坝前后的流速分布规律，现就弯道内有无丁坝两种工况的不同高度水平面的纵向流速分布等值线图进行比较分析。

图4 弯道纵轴线上不同横断面纵向流速模拟值与试验值对比图

图5 弯道纵轴线上不同横断面纵向水位模拟值与实验值对比图

如图6所示，当弯道中无丁坝时，凸岸流速明显大于凹岸流速，最大流速区发生在弯道入口靠近凸岸的局部区域，随着水深的减小，最大流速区的面积不断增大。当弯道内布设丁坝后，最大流速区已由弯道入口处沿纵向发生了移动，并且向弯道纵轴线附近区域延伸，最大流速也由无丁坝时的0.39 m/s，增加到0.53 m/s。与无丁坝时相比，最大流速区的面积有所增加，尤其是在离弯道底部较近的区域更为明显，在靠近凸岸及弯道中心区域流速也有明显的增加，这将有利于减少凸岸的於积。在凹岸区域由于丁坝的束水作用，水流在靠近凹岸区域流速出现了负值，最大负流速为0.2 m/s，出现在第1与第2座丁坝之间的坝区，与之相比第2与第3座丁坝之间和第3座丁坝之后的区域内负流速均较小。每座丁坝后均有回流区存在，回流区的负流速及第1座丁坝前滞流区的流速都明显小于弯道中无丁坝时的流速，这将对防止凹岸遭受冲刷及坝间淤积更有利。当在弯道内布设丁坝群后，弯道内的水流流速分布得到了调整，有利于河岸的防护。

4.3 水面形态分析

如图7(a)所示，弯道内无丁坝时，当水流进入弯道后为提供向心力，使靠近凸岸区域水位降低，靠近凹岸区域水位升高，使水面形成横比降，造成弯道内的水面形态发生变化。

如图7(b)所示，当弯道内布设丁坝后，由于丁坝的壅水作用，使弯道内的水位重新分布，与无丁坝时相比在弯道中心区域以及凸岸区域水位有明显的升高，这将有利于增加航道水深。同时在第1座丁坝前，形成了一个高水位低流速的滞留区，在第3座丁坝后的弯道出口区域，水面线更加平顺，与坝头附近区域相比两座丁坝之间的区域水位变化相对较小。在弯道中心区域沿纵向形成了水面纵比降，尤其是在第1座丁坝附近，纵比降最为明显，最大纵比降为0.005。

图6 弯道处不同平面上纵向流速分布等值线图(单位：m/s)

图7 弯道水位等值线(单位：m)

图8为弯道内有、无丁坝情况下水面横比降的分布图。由图8可见，弯道内无丁坝时，从弯道入口到弯道出口水面横比降有逐渐增大的趋势。当弯道内布设丁坝后，弯道内水面横比降发生了调整，水面横比降沿流向呈明显的双峰型。水流刚进入弯道后受第1座丁坝壅水的影响，在弯道入口的局部区域横比降较无丁坝时略高，从布设丁坝的断面3到弯道出口，布设丁坝后的水面横比降均小于无丁坝的情况。

总之，在弯道内布设丁坝群后，可使主河槽的水深得到增加，水面横比降有所减小，说明丁坝在调整河道水深及稳定弯道水流方面有一定的作用。

图8 弯道水面横比降分布图

4.4 流场结构分析

图9和10分别为有、无丁坝的情况下弯道不同横断面上的流线图及近底面流线图。弯道水流由于水面横比降的存在使弯道横断面形成压力差，导致横向环流产生，最终形成弯道螺旋流。弯道螺旋流的存在将造成凹岸发生冲刷，凸岸发生淤积，对于岸坡的稳定很不利，同时也使弯道的水流流态更为复杂。在弯道内布设丁坝后，如图9(b)所示，由于丁坝的束水作用，使得弯道环流的形成受到抑制。在第1座丁坝前的断面2可明显观察到横向环流尚未发展，布设丁坝后横向水流流向凸岸底部，断面7处在布设丁坝前弯道环流已经形成，布设丁坝后在第2座丁坝前存在一个顺时针方向的漩涡，即文献[16]中所观察到的马蹄涡。由于第1座丁坝的影响，坝后出现了回流区，与断面2相比，回流区与主流区分界线非常明显。从图9(b)中也可清楚的观察到该现象，受纵向水流影响分界面有明显的非恒定性，但分界面位置基本都在丁坝坝头附近，水流在分界面两侧的主流区与回流区不断交换。在第3座丁坝前的断面10，主流区与回流区的分界面更加明显，但由于第2座丁坝与第3座丁坝之间的间距较小，且第2座丁坝的挑流作用没有第1座丁坝明显，回流区并未充分形成就已在坝前绕流，使弯道环流又有一定的发展。在第3座丁坝后的断面13，无丁坝时弯道环流已得到充分发展，布设丁坝后由于受第三座丁坝坝后回流区的影响，弯道环流只在靠近弯道底面附近的区域形成。

图9 弯道不同横断面上模拟的流线图

图10 近底面流线图比较(z=0.03 h)

从图10(a)、10(b)可观察到，布设丁坝后弯道水流的流线有明显区别，每座丁坝后均有回流区存在。其中第1座丁坝后回流区的范围最大，第2座丁坝与第3座丁坝后回流区的范围受第1座丁坝挑流的影响，回流区范围相对较小。因此，与无丁坝时相比，在弯道内布设丁坝群后，弯道内存在明显的主流区与回流区，这将有利于改善弯道水流流态。

5 结 论

(1)采用RNGk-ε紊流模型结合VOF法对60°弯道内布设丁坝前后的流场特性进行了数值模拟研究，并与相关文献的试验数据进行比较，模拟值与实验值吻合较好，验证了本文所采用的数学模型和求解方法的可靠性。

(2)在弯道内布设丁坝群后，弯道内的最大流速及最大流速区的面积都有显著增加并且每座丁坝后均有回流区产生。这将有效防止凹岸区域的冲刷及凸岸区域的淤积，有利于河岸的防护。与无丁坝时相比在弯道中心区域以及凸岸区域水位有明显的升高，在第1座丁坝前有一个高水位低流速的滞留区形成，可见丁坝群能够增加河道水深。

(3)布设丁坝后弯道水流的流线有明显变化，每座丁坝后均有回流区存在。其中第1丁坝后回流区的范围最大，第2座与第3座丁坝后回流区的范围受第1座丁坝挑流的影响，其相对较小。与无丁坝时相比，布设丁坝群后，弯道内存在明显的主流区与回流区，且弯道内水面横比降整体上有所减小，这将有利于改善弯道水流流态。