高速列车底部结构参数对气动阻力作用规律

杨志刚， 毛 懋， 陈 羽

(1. 同济大学 上海地面交通工具风洞中心， 上海 201804;2. 同济大学 上海市地面交通工具空气动力学与热环境模拟重点试验室， 上海 201804; 3. 北京民用飞机技术研究中心， 北京 102211)

高速铁路是在能源和环境约束下解决我国交通运输能力供给不足的重要设施[1].当列车运行速度达到300 km·h-1时，气动阻力占运行总阻力的85%以上[2-3].随着车速的提高和我国高速铁路运营里程的不断增加，高速列车的节能环保运行是车辆设计时面临的重要问题.

高速列车空气动力学的特点是大长细比、近地运行、底部结构复杂和高雷诺数的流动[4].列车在300 km·h-1运行时，8节编组列车，压差阻力与黏性阻力分别占到75%和25%[5].高速列车黏性阻力与车体表面积成正比，在编组长度和乘员空间要求下，减小列车的黏性阻力困难.高速列车底部的转向架区域气动阻力占8车气动总阻力的27.4%[5]，且其主要为压差阻力，Baker[6]指出当地流动结构极为复杂，是高速列车气动减阻的重点.Ido等[7]通过风洞试验发现列车底部的流速对底部结构外形非常敏感.郑循皓等[8]通过数值方法研究了头、尾车末端裙板和外侧导流结构对转向架气动阻力的影响，指出适当改进底部结构有利于减小转向架的气动阻力.杨志刚等[9]分析了裙板对三车编组高速列车气动阻力的影响，表明在头、尾车一位端安装裙板对列车气动减阻最有效.黄志祥[10]通过风洞试验指出车底转向架周围的空腔间隙越小，有利于减小列车气动阻力.陈羽[11]等研究了转向架舱前后导流板对列车气动阻力影响规律，表明不同形式底部导流板的列车总阻力相差可达20%，直式导流板对降低全车气动阻力的效果最好.Niu[12]采用数值方法研究了排障器形状对三车阻力的影响，在无侧风工况下可减阻9.59%.Zhang[13]研究了CRH2型高速列车转向架舱前后导流板的倾角独立变化对气动阻力的影响.上述研究多针对列车底部单一结构外形参数对气动阻力的影响进行分析，缺少底部结构多参数对高速列车气动阻力的影响规律研究.

为了得到高速列车底部结构主要参数对气动阻力的作用规律，对高速列车底部结构的转向架舱长度、裙板高度、转向架舱前缘倒角、后缘倒角，排障器高度、水平曲率、宽度进行样条曲线参数化建模，采用拉丁超立方数值实验方法，通过计算流体力学方法求解得到了底部结构参数对高速列车气动总阻力和头、中、尾各节车气动阻力的作用规律，分析了底部结构参数、流动和气动阻力之间的关系，研究为高速列车底部结构参数的全局气动阻力优化设计提供参考.

1 参数化模型

1.1 列车模型

建立了1∶8缩比的3节编组高速列车参数化模型.模型包含头车、中间车、尾车，其中头、尾车几何外形一致.高速列车模型L×W×H为9 567 mm×408 mm×488 mm.模型包括排障器、转向架舱、转向架、车辆连接处，简化了受电弓、雨刮等车身表面部件.其中头车、尾车的转向架为动力转向架，中间车为拖车转向架，列车及转向架模型如图1所示.转向架舱由舱前壁A面、舱顶壁B面、舱后壁C面、舱内两侧D面组成，如图1d所示.

1.2 底部结构参数化列车建模

本文中定义的底部结构包括3个部分：转向架舱、转向架(含轮对)和排障器.由于转向架结构和功能的复杂性，不对它做几何外形改变，参数化建模针对转向架舱和排障器进行.使用基于样条曲线的建模方法，对转向架舱和排障器设计了7参数变量，并保证车体断面形状不变，如图2所示.

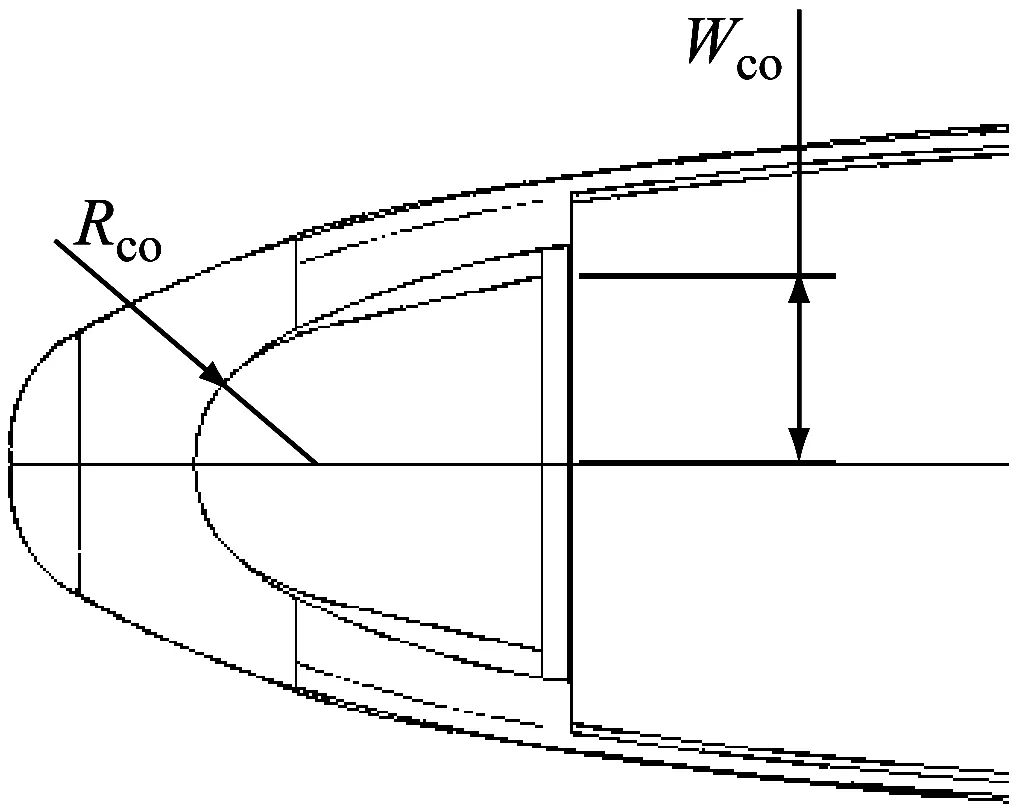
b 排障器参数

转向架舱的4个参数包括：转向架舱长度l、裙板高度h1、转向架舱前缘倒角Rf、转向架舱后缘倒角Rr；排障器的3个参数包括：排障器厚度h2、排障器水平曲率控制控制点Rco、排障器宽度Wco.

转向架舱长度l的变化范围参考我国即有的高速列车转向架舱尺寸，裙板高度变化范围从无裙板到全覆盖裙板，排障器底部距离轨面17 mm以上(1∶8模型)，排障器宽度小于车体宽度，水平曲率控制点不超过鼻尖位置，如表1所示.

表1 参数变化范围

1.3 基于拉丁超立方的数值实验设计

底部结构包含7个变量参数，取值范围较大且每个参数至少需要3水平，如果全部考虑7个参数的所有水平(即全因子法)，需要计算的仿真次数至少为2 187，需要消耗大量计算资源.

拉丁超立方抽样是一种从多元参数分布中近似随机抽样的方法，属于分层抽样技术，常用于计算机实验或蒙特卡洛积分.Mckay等[14]人于1979年提出了拉丁超立方抽样，原理是：首先假设样本空间S有K个变量，则变量记为x1，…，xk；其次确定模拟次数N，则对于变量xi(i=1，…，K)，其样本空间被分割为N个互不重叠的子区间，每个子区间内进行等概率的随机抽样；最后，每个样本由一组xij(i=1，…，K,j=1，…，N)组成，其形式为Xi=[xi1，…，xiN](i=1，…，K).

1981年，Iman等[15]进一步发展了该方法.该方法把每个因子的设计空间均匀划分，选取好点后再将每个因子的水平随机组合，以此来定义设计矩阵的样本点.改进方法的优点是试验次数大于因子数即可，在样本空间可以做到均匀取点.该方法较好给出各个因素的相关性系数，得到参数对气动阻力的作用规律[16].对于本文，设计变化参数K=7，设计模拟次数N=20.利用Isight软件的DOE实验设计模块，对表1所示样本空间抽取了20个样本组合.试验设计表如下所示，加上基础样本点0，共计21个样本点，试验设计见表2：

2 数值方法

2.1 计算方法

采用商业软件FLUENT进行空气动力学计算.列车运行速度为250 km·h-1，对应马赫数为0.204，作为不可压缩流体进行求解.使用SIMPLE算法求解方程，先使用1阶迎风格式计算，再换用2阶迎风格式进行迭代.由于转向架区域空腔和尾迹的非定常涡脱落，使得列车阻力系数无法收敛到一个稳定的定常解，在迭代达到一定值时，气动阻力系数在一个较小的范围内呈现准周期震荡，取呈现准周期性震荡时若干周期的平均值作为列车气动阻力系数.

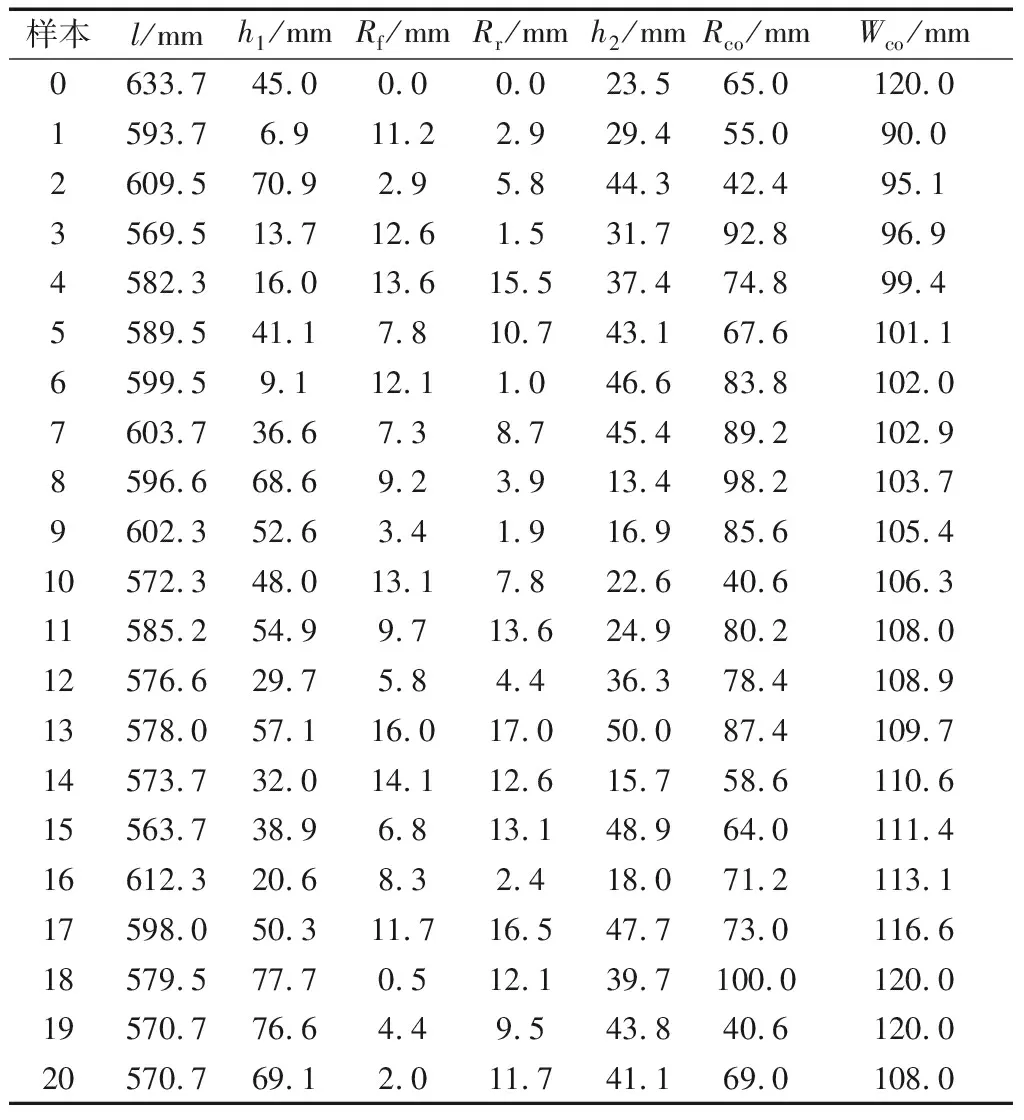
表2 高速列车底部结构参数化试验设计表

计算域和计算网格如图3a和3b所示，其大小为：入口距离头车鼻尖1L、出口距离尾车鼻尖2L、两侧距离车体中心线0.5L、高度10H.计算域两侧以及上边界设为无反射对称边界条件，入口为速度入口，采用均匀来流，计算域出口设为压力出口，车体及转向架表面均为无滑移固壁边界，采用移动地面边界条件来模拟真实列车与地面的相对运动，地面移动速度与入口速度相等.采用三角形面网格和四面体网格，体网格数约为1 600万.湍流模型采用了可实现的k-ε两方程湍流模型，同时配合使用非平衡壁面函数，其考虑了压力梯度效应，可以较好地反映分离、再附着等问题[17].在车体与地面划分了边界层网格，边界层第1层高度为1 mm，共5层，增长率1.15.计算得到车体表面平均y+为35，符合非平衡壁面函数的要求，车体边界层网格如图3 c所示.

2.2 计算方法验证

在同济大学上海地面交通工具风洞中心进行1∶8缩比CRH3型列车空气动力学试验，如图4所示.试验中均匀来流，风速从120 km·h-1～250km·h-1，试验中地面为静止地面，来流湍流强度为0.5%，测力的天平为盒式天平，内置安装在3节列车模型的重心位置.天平上表面为受力感应面，通过应力应变片将力信号转为电信号输出.车体表面布置测压孔，静压测量采用4组64路电子扫描阀获得.在0°风向角的情况下测量了列车的气动阻力系数Cd和车体表面静压系数Cp.上述系数定义如下：

(1)

(2)

式中:ρ为空气密度，试验中来流Ma数小于0.3，故取1.225 kg·m-3；v为来流速度；A为参考面积，试验中取A=0.181 m2；p0为大气压，环境温度约为20℃；大气压取101 325 Pa；p为绝对压力值；Fd为气动阻力.

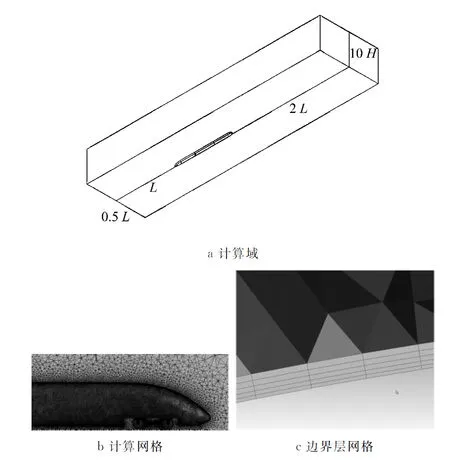
图3 计算域和计算网格

图4 风洞试验布置

采用与2.1节相同的计算方法建立CRH3型高速列车数值计算模型，地面为固定壁面边界条件，风速与试验中250 km·h-1工况一致.研究了计算精度与网格数量的关系，表3给出了不同网格密度(888万、1 200万、1 600万、2 600万和3 200万)的算例与风洞实验结果的对比，1 600万网格总阻力系数与2 600万、3 200万网格的计算偏差分别为3.6%、4.2%，与试验结果偏差为1%.图5给出了不同网格数下头、中、尾三车的阻力分布，各节车阻力系数分布规律一致，头、中、尾三车1 600万网格与2 600万、3 200万网格的计算偏差分别为2.6%、1.6%，6.8%、8.4%，6.0%、4.0%.图6给出了1 600万网格下头车车体上表面对称中截面静压系数对比，表面静压系数分布与风洞试验测得趋势一致.因此考虑计算精度及计算资源，本文参数化模型数值计算均采用1 600万网格进行计算与分析.

表3 气动阻力计算与试验对比

图5 气动阻力系数

图6 试验与计算表面压力系数对比

3 底部结构参数对阻力影响规律

通过数值计算，得到了21个样本点的各节车和三车总气动阻力系数，如表4所示.阻力系数定义见式(1)，其中参考面积为各个样本点模型的正投影面积.三车的总阻力系数变化范围为0.317～0.435，极差值为0.118，列车底部结构参数对三车气动阻力有重要影响，最小样本点S2、S18比最大样本点S16的阻力系数减小了27.1%.

底部结构参数对头、中间、尾车的气动阻力影响极差值分别为0.080、0.038和0.026，即底部结构参数的影响阻力系数绝对值：头车>中间车>尾车，分别比最大样本点减小了37%、39%和22%.由于中间车不存在类似头、尾车外形的压差阻力，底部结构参数对气动阻力影响比例最大的是中间车.

表4 样本点阻力系数

3.1 底部结构参数对三车阻力的作用规律

将高速列车三车总阻力分为车体和底部结构阻力两部分.其中底部结构的气动阻力包括排障器、转向架、转向架舱三部分的气动阻力.除上述底部结构外的均为车体部分.

图7给出样本点的车体和底部结构阻力系数柱状堆积图，坐标横轴按气动总阻力由小到大的顺序排列，如S18代表样本点18.拉丁超立方分布的21个样本点车体阻力系数在0.204～0.218之间，车体阻力系数极差值为0.014.三车编组的底部结构阻力系数在0.105～0.221之间，底部结构气动阻力系数极差值为0.116.底部结构气动阻力系数极差值比车体气动阻力系数极差值大一个数量级.底部结构的气动阻力压差阻力绝对主导，占比在97.8%以上.

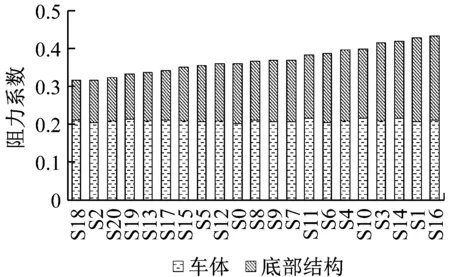
图7 三车车体与底部结构阻力系数

同时，图8给出底部结构中排障器、转向架舱和转向架三个部件的气动阻力系数.横坐标排序为各样本点的底部结构气动阻力系数由大到小排列.列车底部结构的阻力最小的5个样本点为S18、S2、S20、S19、S13，与三车气动阻力最小的5个样本点一致；底部结构阻力最大的5个样本点有S4、S14、S3、S16、S1，除S4外其余均为三车气动阻力最大样本点，且S4的三车总阻力在所有样本点也为高阻力车体.由上述可知，底部结构参数主要影响底部结构自身的气动阻力，进而决定了三车气动阻力值的大小.

由图8还可知，三车气动阻力最小的5个样本点中，排障器阻力系数平均值为0.027，占底部结构阻力比例平均为22.3%；阻力最大的5个样本点，排障器阻力系数平均值为0.012，占底部结构阻力比例平均为6.0%.表明三车编组的低气动阻力车体中，排障器的气动阻力值和其在底部结构中的占比大于高气动阻力车体.

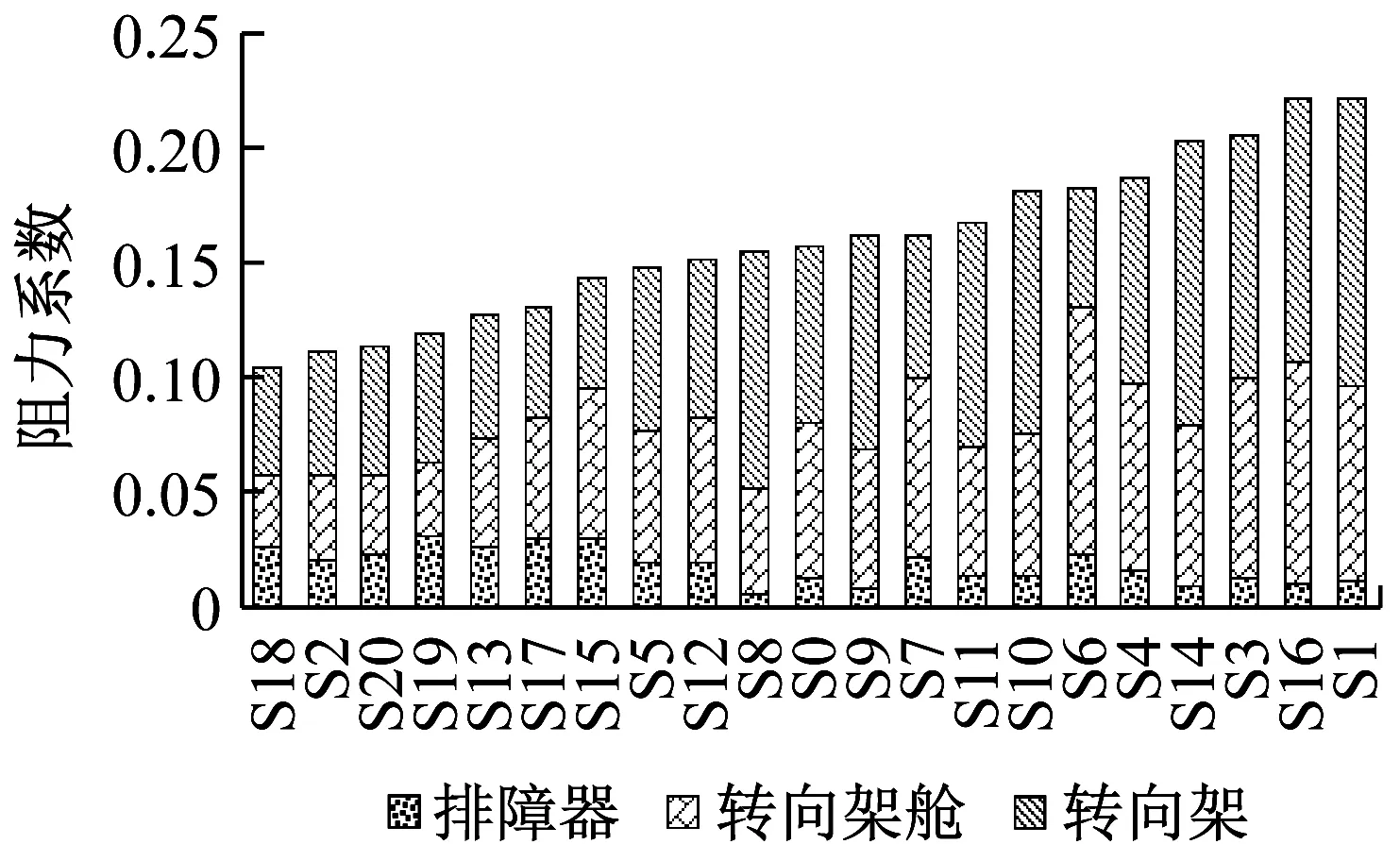
图8 三车底部结构阻力系数

为研究底部结构各参数对三车气动阻力的影响相关性，给出各参数的对整车阻力的相关系数，如下图9所示.对于优化拉丁超立方样本点分布，其为非正态分布，采用Spearman的秩相关系数来评估，该相关系数绝对值的大小排序仅代表了底部结构各个参数影响的重要程度，相关系数的取值范围[-1,1]，相关系数为负即负相关，表示随着参数数值增加气动阻力减小，相关系数为正即正相关，表示随着参数数值增大气动阻力系数增加.其数值大小不具有含义[18]，其定义如下：

(3)

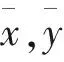
对于三车编组的气动总阻力系数，裙板高度、排障器厚度、转向架舱后缘倒角、排障器宽度和过度形式、转向架舱长度这6个参数均为负相关，转向架舱前缘倒角为正相关.7个底部结构设计参数对三车气动阻力影响的重要程度排序依次为：裙板高度>排障器厚度>转向架舱前缘倒角>转向架舱后缘倒角>排障器宽度>排障器水平曲率>转向架舱长度.

图9 底部参数与三车气动阻力相关系数

3.2 底部参数对各节车气动阻力作用规律

3.2.1底部结构参数对头车阻力作用规律

图10给出头车的车体与底部结构气动阻力柱状堆积图.头车车体气动阻力变化范围0.071～0.095，阻力差值为0.024，底部结构的气动阻力变化范围0.060～0.120，极差值为0.060.底部结构气动阻力系数极差值是车体的2.5倍.

图10 头车车体与底部结构阻力分布

图11给出了头车底部结构部件的气动阻力系数.头车底部结构参数影响底部结构自身的阻力系数，进而影响头车总阻力系数.对于头车气动阻力最小的5个样本点中，排障器阻力系数平均值为0.021，占底部结构阻力比例平均为31.4%；阻力最大的5个样本点，排障器阻力系数平均值为0.009，占底部结构阻力比例平均为8.7%.表明头车的低气动阻力车体中，排障器的气动阻力值和其在底部结构中的占比远大于高气动阻力车体.

图11 头车底部结构阻力分布

根据式(3)得到头车气动阻力的秩相关系数，如图12所示.排障器厚度、裙板高度、转向架舱后缘倒角、排障器宽度和水平曲率这5个参数为负相关，转向架舱长度和前缘倒角为正相关.底部结构参数对头车气动阻力影响的重要程度排序依次为：排障器厚度>裙板高度>转向架舱后缘倒角>转向架舱前缘倒角>转向架舱长度>排障器水平曲率>排障器宽度.上述结果表明：底部结构参数对头车气动阻力影响排序与其对三车气动阻力的不同.

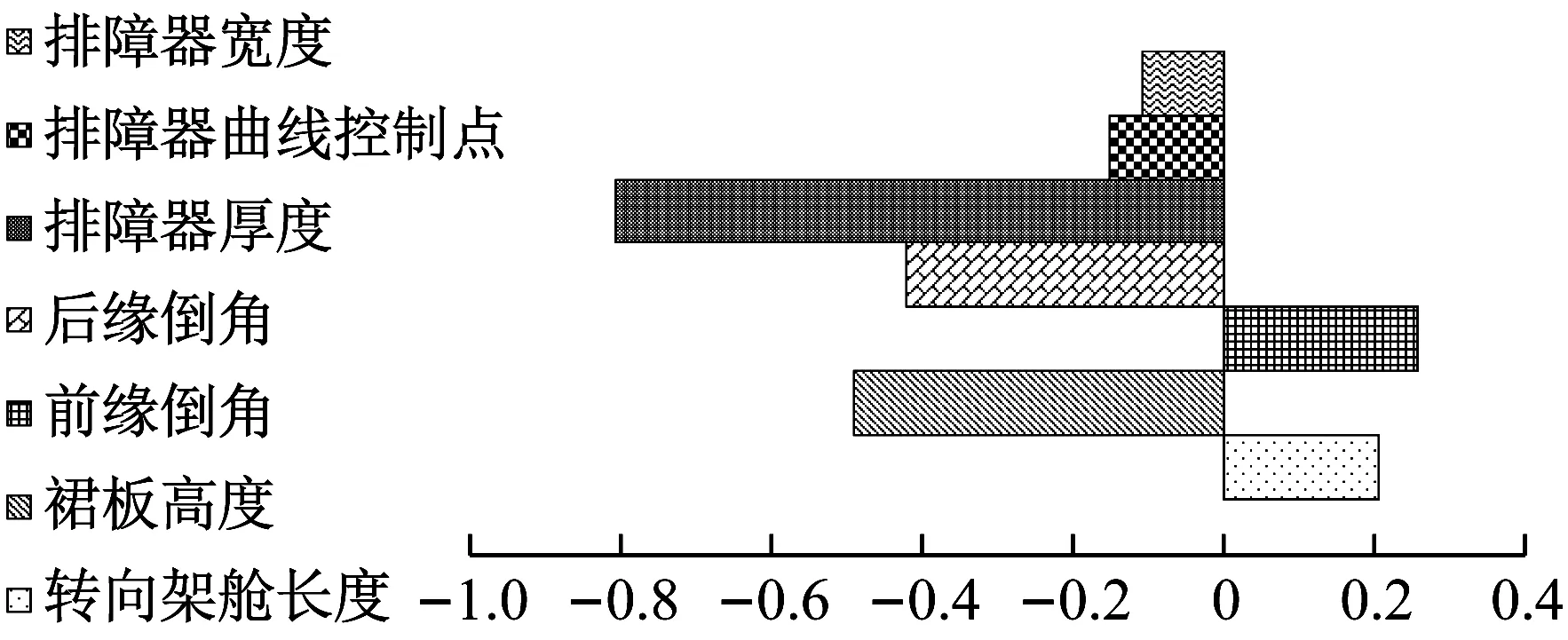
图12 底部结构参数与头车阻力相关系数

3.2.2底部结构参数对中间车阻力作用规律

图13给出中间车的车体和底部结构阻力系数柱状堆积图.中间车车体阻力系数在0.037～0.048之间，车体阻力系数极差值为0.011.底部结构阻力系数在0.015～0.055之间，底部结构气动阻力系数极差值为0.040.底部结构气动阻力系数极差值为车体的3.6倍.图14给出底部结构中转向架舱、转向架两个部件的气动阻力系数.底部结构阻力最大的样本点，中间车总阻力也为最大值.

图13 中间车车体与底部结构阻力

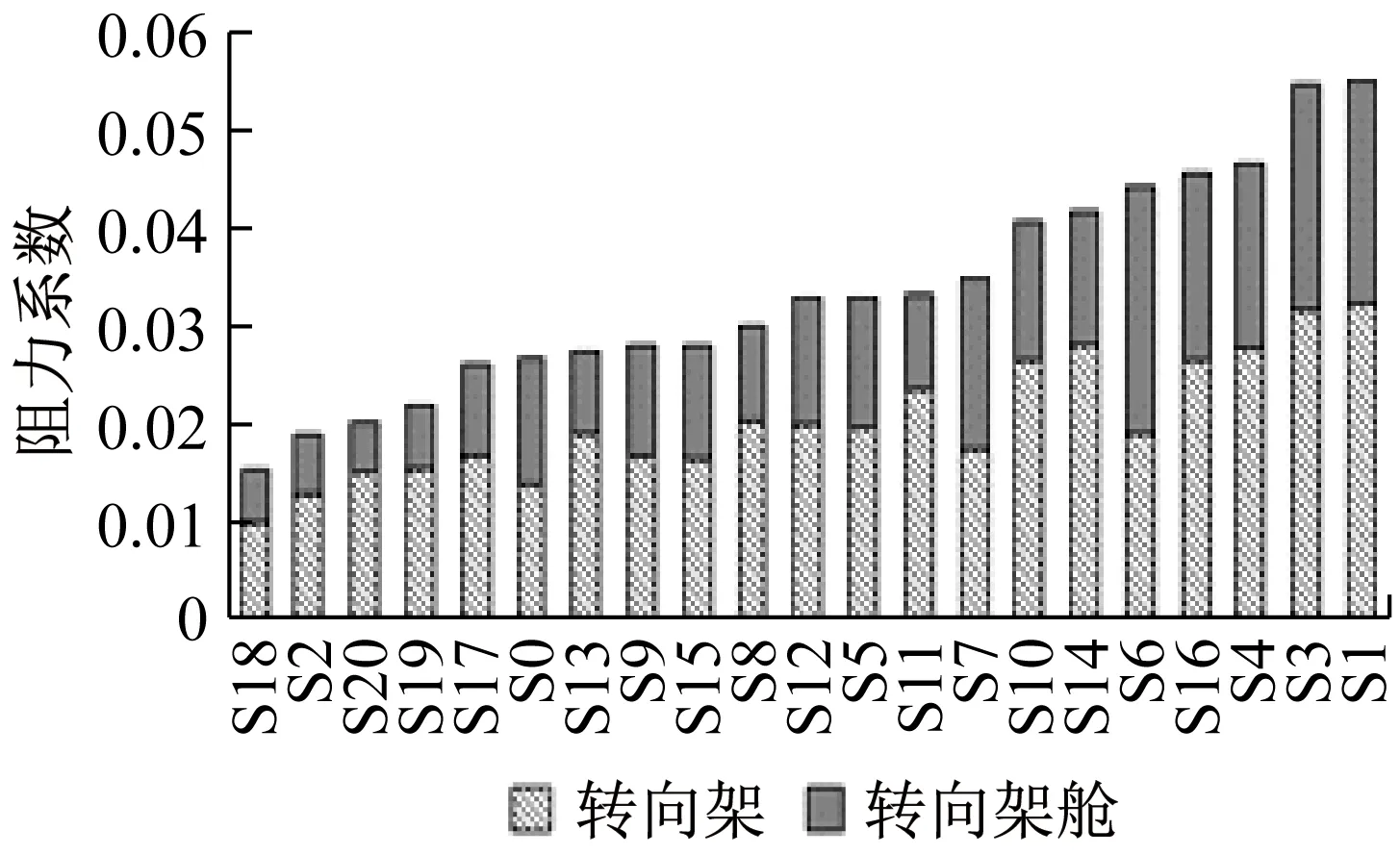
图14 中间车底部结构阻力分布

相关系数如图15所示，排障器厚度、裙板高度、转向架舱后缘倒角、排障器宽度、水平曲率和转向架舱长度这6个参数均为负相关，前缘倒角为正相关.由于头车排障器影响中间车底部气流状态，所以排障器对中间车阻力也有影响.底部结构参数对中间车气动阻力影响的排序依次为：裙板高度>转向架舱前缘倒角>排障器宽度>转向架舱后缘倒角>转向架舱长度>排障器厚度>排障器水平曲率.中间车底部结构参数影响的排序不同于头车.

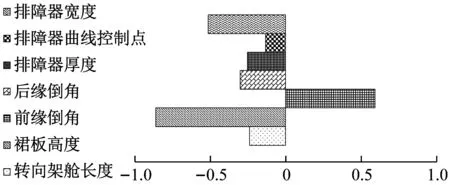
图15 底部参数与中间车阻力相关系数

Fig.15 Correlation coefficients between underbody parameters and aerodynamic drag of middle car

3.2.3底部结构参数对尾车阻力作用规律

图16给出尾车的车体和底部结构阻力系数柱状堆积图.尾车车体阻力系数在0.078～0.095之间，车体阻力系数极差值为0.017.尾车的底部结构阻力系数在0.024～0.061之间，样本点底部结构气动阻力系数极差值为0.037.

图16 尾车车体与底部结构阻力占比

图17分别给出尾车转向架、转向架舱、排障器的气动阻力系数.底部结构阻力仍然影响了尾车的阻力系数.各个样本点的排障器阻力系数平均值为0.004，远小于头车排障器.

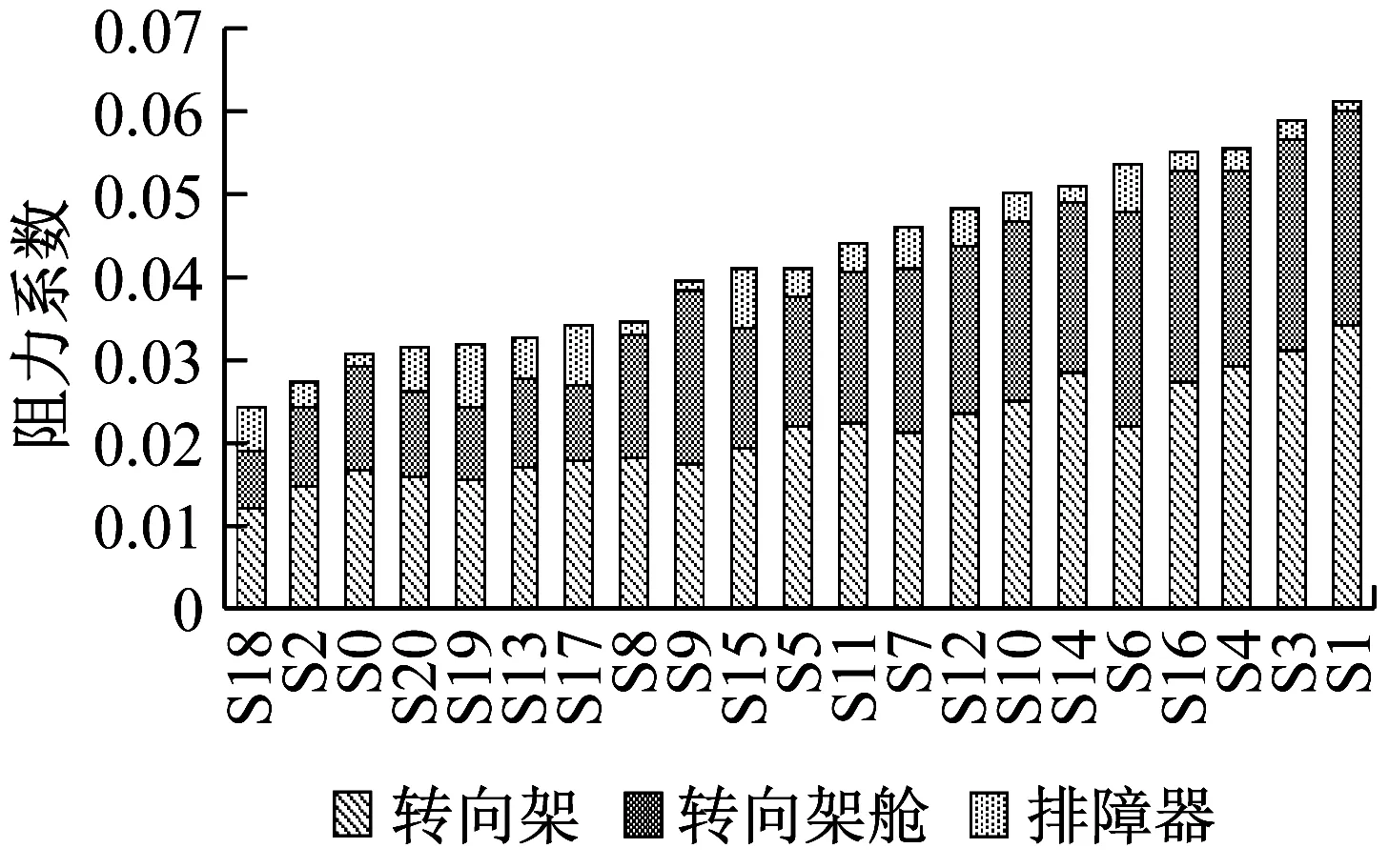
图17 尾车底部结构阻力分布

底部参数与尾车气动阻力的相关系数如图18所示，其中排障器宽度、水平曲线控制点、转向架舱长度为负相关，排障器厚度、转向架舱后缘倒角、前缘倒角为正相关.参数影响阻力的排序依次为：裙板高度>转向架舱前缘倒角>转向架舱长度>排障器宽度>排障器水平曲率>排障器厚度>转向架舱后缘倒角.可以看到，尾车裙板高度高负相关，前缘倒角高正相关，与中间车的结论一致.排障器参数相关系数排序靠后，由于头、尾车对称设计，虽然尾车外形与头车一致，但是底部结构参数对气动阻力的影响规律与头车不同.

3.3 底部结构参数对流场影响分析

将气动阻力系数最大和最小的各5个样本点分别定义为高阻力和低阻力样本点.低阻力样本点为：

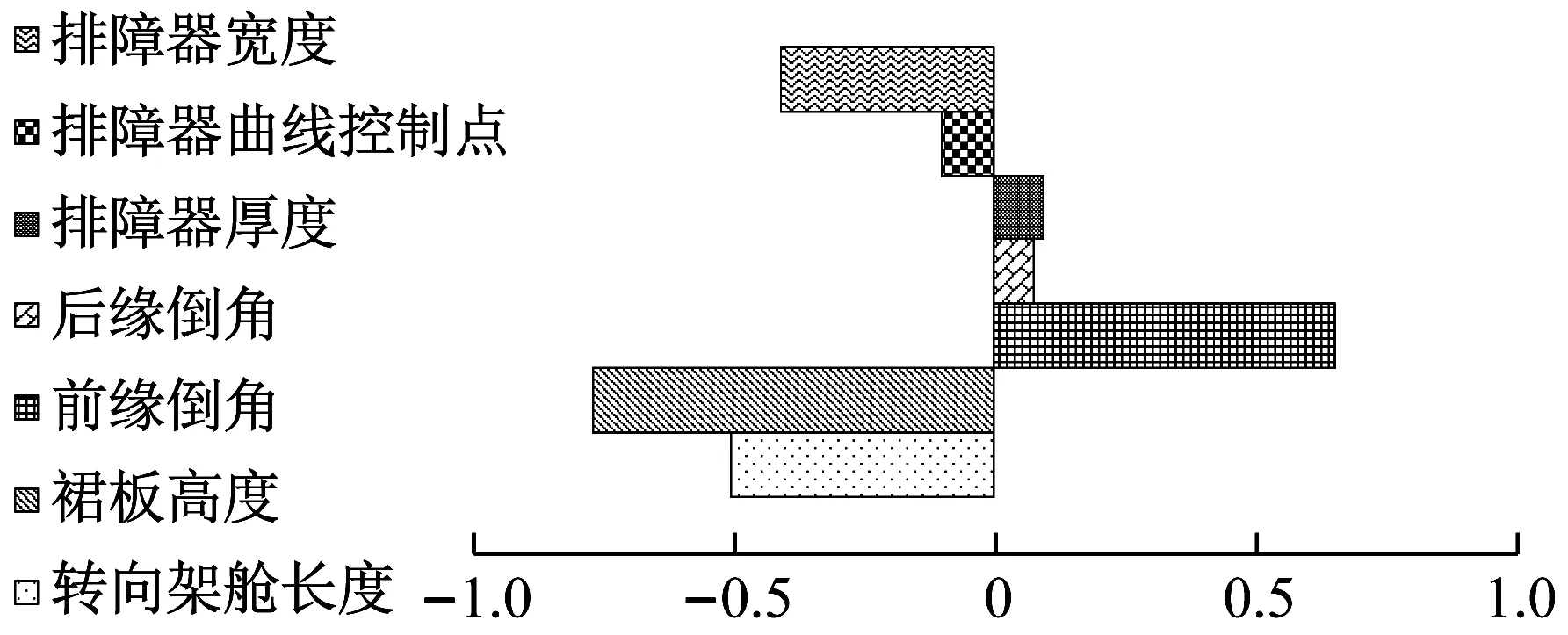
图18 底部参数与尾车阻力相关系数

S18、S2、S20、S19、S13；高阻力样本点为：S16、S1、S14、S3、S10.图19为高速列车离地间隙1/2高度时两组样本点列车底部X方向速度分布，低气动阻力样本点速度曲线为实线，高气动阻力样本点的速度曲线为虚线.

由图19可知，高气动阻力样本底部流速均明显高于低阻力样本点.列车底部结构气动阻力是转向架舱、转向架、排障器相互影响的结果，由于底部参数改变导致底部平均流速变化，低阻力样本点列车底部处于更低的来流之中，因此来流动压减小，转向架和转向架舱的滞止压力降低.上述原因是决定三车总气动阻力的主要因素.

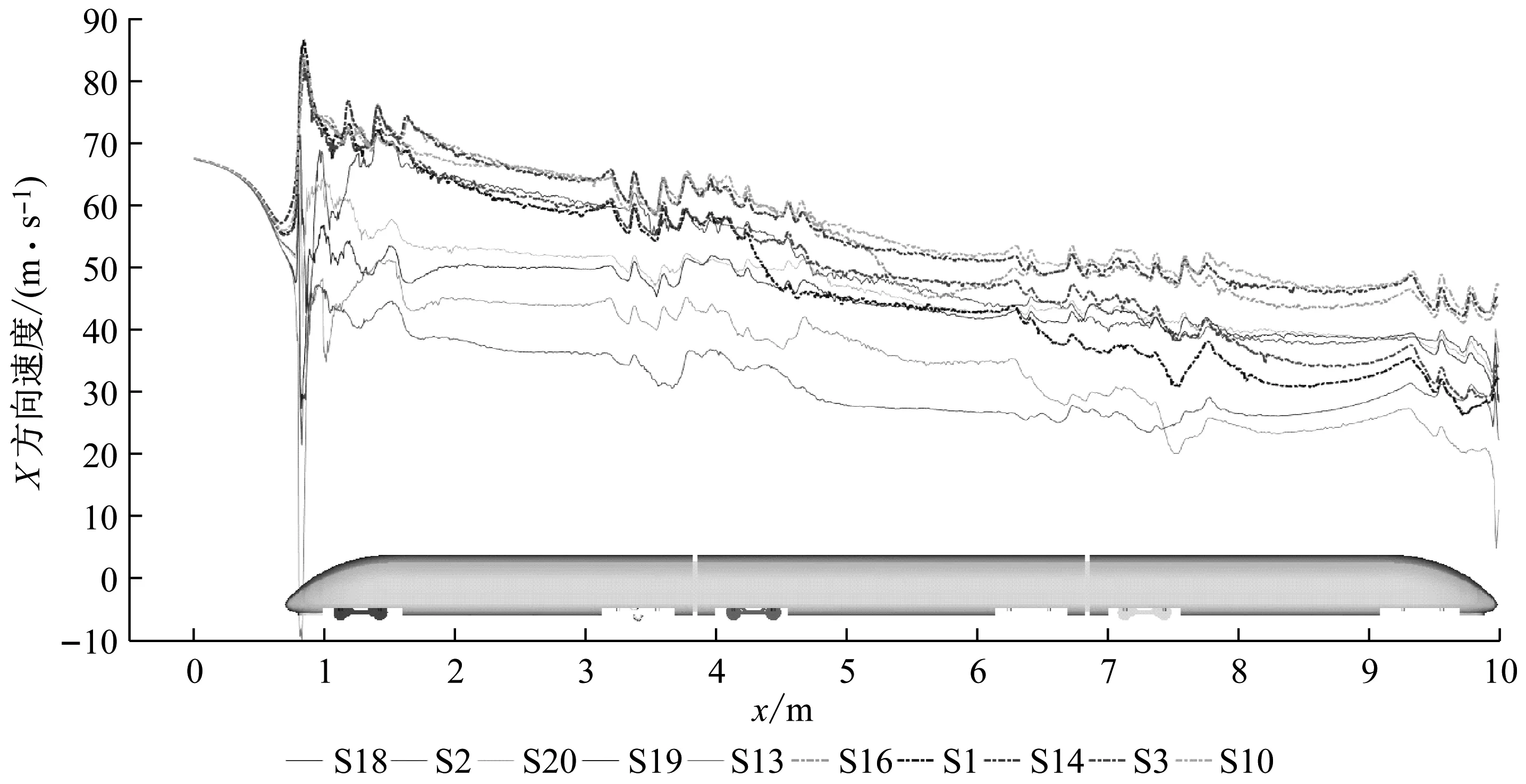
图19 高阻力与低阻力样本点列车底部X方向速度对比

图20给出高阻力和低阻力三车中部车体下方速度型分布，头车底部高阻力车体较低阻力车体流速平均大20 m·s-1，与Zhang[13]研究底部导流板对列车底部流速的影响规律相似.随着流动向下游发展，高阻力车体与低阻力车体底部流速差减小，在中间车中部两者平均差值为12 m·s-1，在尾车中部平均差值为4 m·s-1.上述流场结构差异使得头车的气动阻力极差值大于中间车和尾车.

图20 列车底部X方向速度分布

Fig.20Xvelocity profile underneath train body

对于头车的底部结构参数，排障器厚度最重要的影响参数.图21给出排障器差异最大的两个样本点S8和S15，对比分析头车排障器对流场的影响原因.气流在经过头车底部时，由于S15排障器厚度的增加，排障器与地面间隙减小，列车底部流动平均速度降低，转向架前方来流速度减小，来流动压减小使得转向架上滞止压力降低，底部结构气动阻力减小.

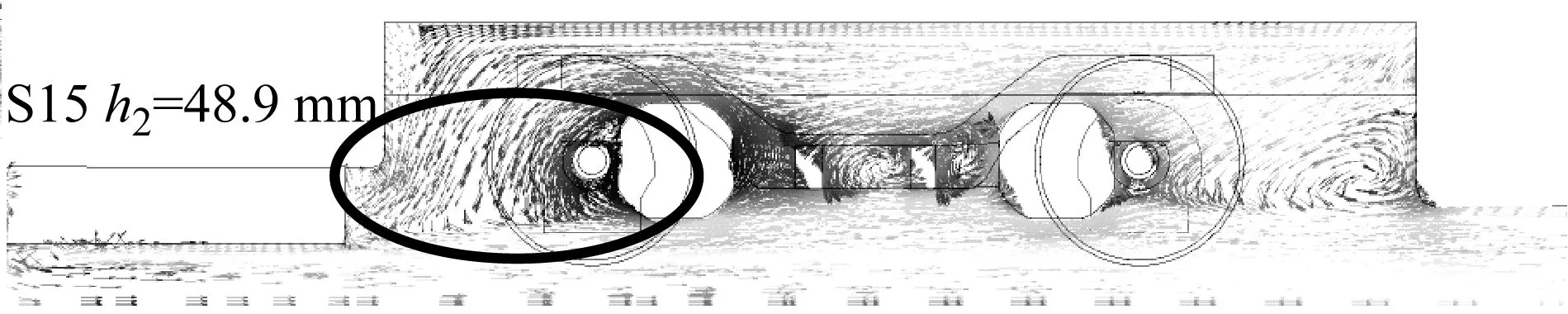
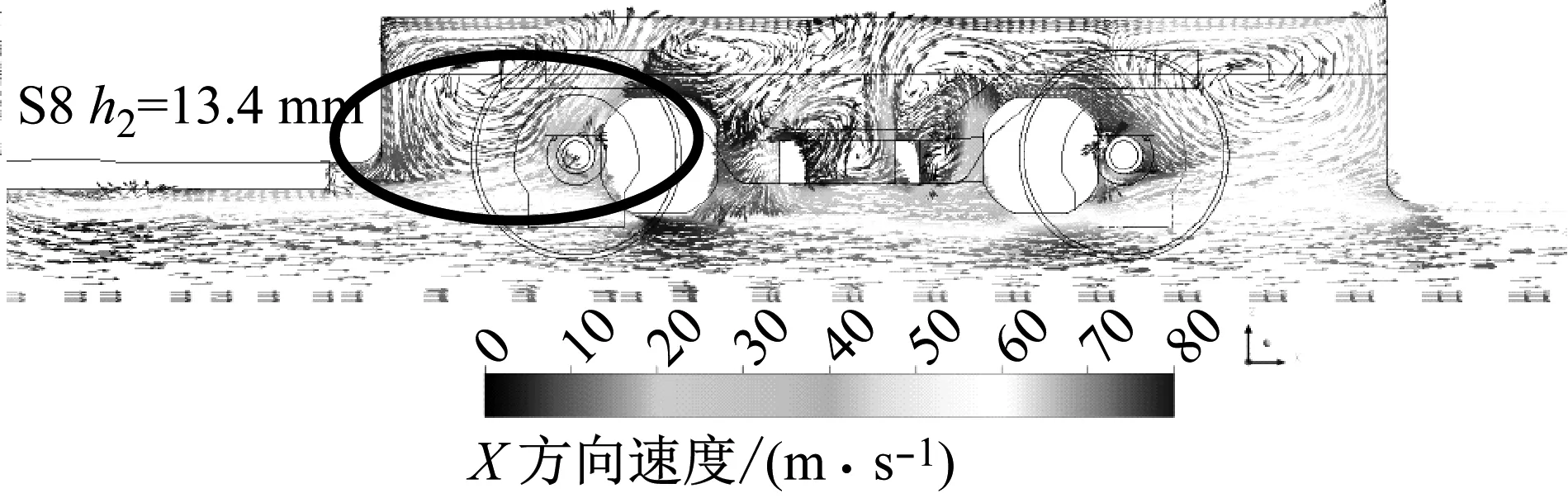
图21 S8和S15样本点头车底部速度矢量图

在底部结构参数中，转向架舱前缘倒角也呈现明显的正相关性，且在中间车、尾车中.通过图22可以看到，较大的前缘倒角使得剪切层上抛对转向架造成气流冲击，S13较S18转向架下部流速大5 m·s-1以上，更高的气流速度使得舱内转向架的气动阻力增加.

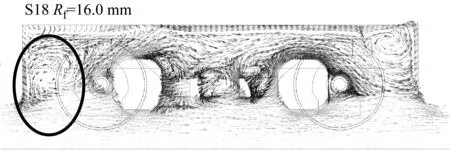
a 速度矢量图

b 速度差值云图

通过图23的S6和S18水平截面的速度矢量图对比，可以看到裙板高度的增加减少了进入转向架舱内的气流，舱内的流速降低，减小了转向架和转向架舱的气动阻力.

图23 S6和S18头车转向架舱水平面速度矢量图

4 结论

本文对高速列车底部结构进行参数化，采用拉丁超立方试验设计的和计算流体力学的方法，研究了7个主要底部结构参数对高速列车气动阻力的作用规律，研究结果表明：

(1) 底部结构参数主要影响底部结构自身的气动阻力，进而影响三车气动阻力值的大小，根据拉丁超立方数值试验得到所有样本点的三车、头、中、尾车阻力系数极差值分别为0.118、0.080、0.038和0.031，最小样本点较最大样本点气动阻力分别减小了27%、37%、39%和22%；

(2) 底部结构参数对于三车总阻力和各节车的影响规律不同，其中三车主要影响参数为裙板高度>排障器厚度>转向架舱前缘倒角；头车主要影响参数为排障器厚度>裙板高度>转向架舱后缘倒角；中间车主要影响参数为裙板高度>转向架舱前缘倒角；尾车主要影响参数为裙板高度>转向架舱前缘倒角>转向架舱长度，有必要考虑针对头、中、尾三车底部结构分别进行气动设计，以达到最优减阻效果；

(3) 列车底部结构参数主要通过改变列车底部来流速度来影响列车底部结构气动阻力，进而作用影响三车气动阻力.