基于驾驶模拟实验的山区高速公路运行速度建模

郭启明， 王雪松， 陈志贵

(同济大学 道路与交通工程教育部重点实验室，上海 201804)

自20世纪70年代起，道路交通安全问题在世界范围内凸显，欧美一些国家以设计更安全的道路为目标，提出了运行速度的概念[1].运行速度一般取自由流车速分布中的85%分位数V85，反映的是绝大多数驾驶员在当前道路线形设计条件下所选择的行驶速度.

在自由流状态下，驾驶员的车速主要受道路线形变化的影响，短距离内剧烈的车速变化往往预示着不连续的线形设计，因此基于运行速度曲线可以检验和评价线形设计的连续性和协调性，指导线路的优化.这一定量的安全评价方案被许多国家引入规范体系中.国际上最具代表性的成果是美国的交互式道路安全设计模型(Interactive Highway Safety Design Model)[2].我国交通部于2004年颁布了《公路项目安全性评价指南》[3]，指南在2016年升级为《公路项目安全性评价规范》[4]，规范在参考欧美标准的基础上，结合我国国情和大量断面测速数据，系统构建了高速公路、一级公路、二级公路和三级公路的运行车速预测模型组[5].

为了在设计阶段预测运行速度曲线用于道路线形设计改良，国内外学者建立了大量的运行速度预测模型，研究的道路类型有高速公路、双车道公路、单车道公路等，使用了线性回归、面板数据回归、神经网络等方法[6].LAMM等人[7]是最早开始速度建模研究的学者，他们基于纽约州261个平曲线的雷达枪测速结果建立了以圆曲线半径为解释变量的运行速度预测模型.FITZPATRICK等人[8]根据78个位点的实测车速数据将高速公路划分为5类并分别建立了运行速度预测模型，模型中使用的解释变量包括平曲线曲率、偏转角、直线段长度、路段坡度等.徐进[9]等人在传统的运行车速模型的基础上，研究了曲线转角、通道宽度以及不同交通量条件对速度的影响.最新的《公路项目安全性评价规范》[4]将公路线形划分为平直、平曲线、纵坡、弯坡组合及其他路段，选择路段起终点和曲线段中点作为速度特征点构建预测模型，模型中包含了前一车速特征点的预测速度值，采用迭代的方式考虑了上游路段单元的影响.

由于目前运行速度建模研究大多基于断面测速数据，预测运行速度曲线时，一般先预测路段特征点的运行速度，而后基于一定的驾驶行为假设判断特征点间的车速变化.MEDINA等人[10]在每个平曲线内采集7个特征点进行断面测速，研究发现驾驶员在进入平曲线缓和段前就开始减速且减速过程持续到平曲线内部，在不同半径的平曲线上，驾驶员的车速选择并不一致.这一问题在Mcfadden[11]等人的早期断面测速研究和最新的基于GPS试验车的车速建模研究[12]中均得到印证：路段特征点(例如平曲线起点、中点和终点)未必是车速变化的特征点(例如最大、最小车速点)，定点测速的方法不适用于预测连续的运行速度曲线.现有车速预测模型的另一个缺陷是较为简单的驾驶行为假设.对于平曲线及纵坡分布密集的山区高速公路，驾驶员的车速选择不仅受当前路段几何设计参数的影响，还与前后邻近的一个甚至数个路段单元有关.但是在大多数速度预测模型中，模型的解释变量仅仅使用了当前路段的线形参数，且直接假设车辆减速进入平曲线和加速离开平曲线[12].

新型的数据采集手段，如GPS试验车和驾驶模拟器，可以获取高精度的连续车速数据，为更好地预测运行速度曲线提供了可能.具有运动系统的高仿真驾驶模拟器被认为是研究驾驶行为的理想实验工具[13].与GPS试验车相比，驾驶模拟器可以通过场景控制排除包括天气、光线、环境车辆、驾驶员情绪在内的各种非道路因素的影响，具有更好的实验可控性[14].

随着我国东部省市高速公路网络的完善，未来高速公路的主要建设区将集中在中西部地区.中西部省份多山多河谷，地形条件复杂，高速公路容易出现连续平曲线、弯坡组合的几何线形设计，研究和预测复杂路段上的车速变化具有重要意义.

1 实验与数据准备

1.1 驾驶模拟实验

实验人员：通过社会招募，共有21名驾驶员参与驾驶模拟实验并采集到有效的实验数据.驾驶员样本的年龄分布在23～59岁之间，平均年龄36.5岁，职业主要为交通运输业、公司职工及高校教职人员，受试驾驶员中超过半数驾驶员表示经常在高速公路上驾驶.每名参与实验的驾驶员要求总驾驶里程至少达到10 000 km，且每年平均驾驶里程不少于3 000 km.研究使用的数据均为驾驶员首次驾驶实验路段的数据.

实验设备：使用同济大学驾驶模拟器开展实验，如图1所示.模拟器具有8自由度运动系统，X—Y方向的运动范围为20×5 m；舱体为封闭刚性结构，内置梅甘娜Ⅲ型仿真车辆，车辆去除了发动机并加载了方向盘、刹车等设备的力反馈系统及数据输入输出设备；视景系统通过5个内置投影仪将范围为250°×40°的场景投射到柱形屏幕上，车旁和车内后视镜由LED屏幕显示场景变化.通过眩晕测试、停车距离测试以及交通标志测试对模拟器的仿真效果进行检验，结果表明同济大学驾驶模拟器能模拟真实且稳定的驾驶场景，不会引起驾驶员眩晕等不适症状，所采集的实验数据可以反映驾驶员真实的驾驶行为.

图1 同济大学高仿真驾驶模拟器

实验道路：按照湖南省永吉高速公路的CAD设计图纸及周边山体的等高线地图构建驾驶场景，道路模型考虑平曲线、纵断面、横断面要素以及路侧遮挡.实验道路设计速度为100，双向4车道，连续弯道和平纵组合路段多，圆曲线半径区间为400 m～2 000 m，纵坡区间为-6%～4%，总长24 km，包含两个总长9.4 km的隧道，以平曲线作为划分单元，道路的两个方向各包含53个路段，其中直线段16个，曲线段37个，平纵线形条件覆盖广，组合形式丰富，属于典型的山区高速公路，具有较好的代表性.实验道路从北向南的高程和曲率变化图如图2所示，图中负曲率值表示左转弯道，正曲率值表示右转弯道.

实验设计：模拟驾驶的实验条件设置为白天，路面干燥且无环境车辆，驾驶员实验过程中不允许使用手机等电子设备，以排除非道路因素的干扰.实验包括准备、试驾和正式实验3个部分：准备阶段驾驶员填写问卷并被告知实验要求及注意事项；试驾阶段驾驶员在另一条山区高速公路上行驶约10 min时间以熟悉模拟器车辆的操作；正式实验时要求驾驶员按照正常驾驶习惯完成实验，为避免驾驶员变道时的减速行为影响实验结果，建议驾驶员在非必要情况下不更换车道.实验结束后受试者将填写测试评价问卷，出现眩晕等不适症状的驾驶员样本将不作为分析数据.问卷结果表明参与实验的驾驶员没有出现不适症状，驾驶场景逼真，实验数据有效.

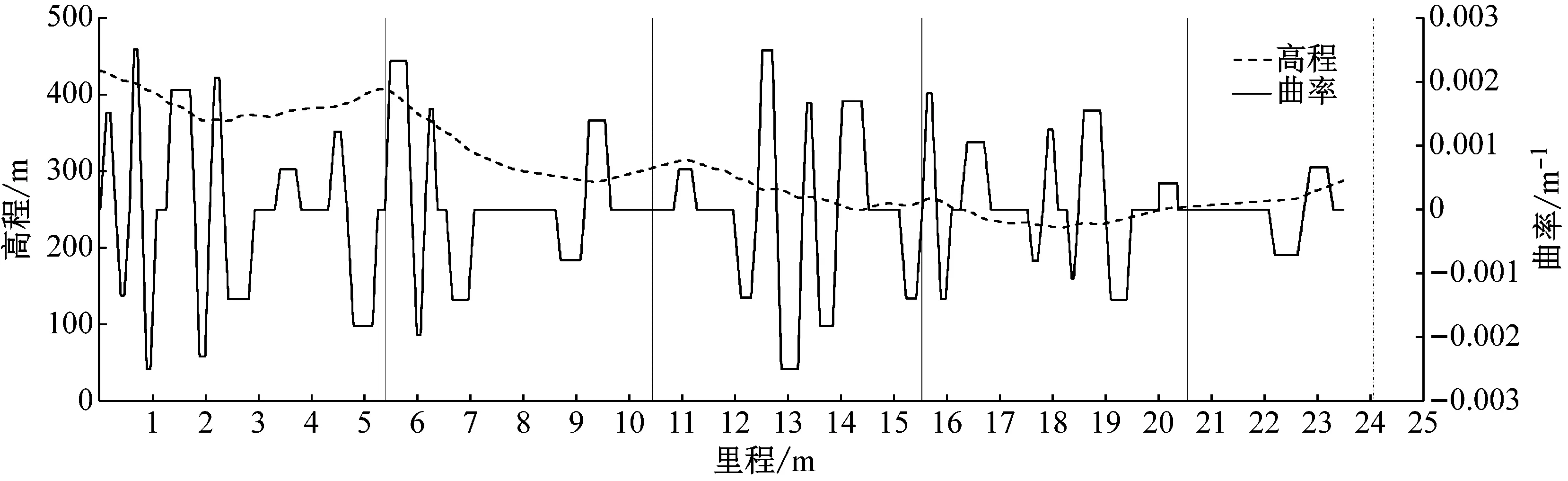
图2 实验道路线形参数变化

1.2 数据准备

由于驾驶模拟器按照固定频率20 Hz采集数据，为了将不同驾驶员的车速数据匹配到相同位置上，按照5 m的间隔集计速度数据，得到每个驾驶员在各个5 m间隔内的平均车速.在每个5 m间隔的区间上，根据21名驾驶员的车速分布提取85%分位数值，得到运行速度.

图3中的灰色曲线绘制了21名驾驶员的原始速度变化曲线图，黑色曲线为提取的运行速度曲线.从图中可以看到尽管不同驾驶员加减速的时机和选择的车速存在明显的差异，但在经过线形受限的位置时均有相似的减速行为，反映了线形变化对驾驶员速度选择的影响.

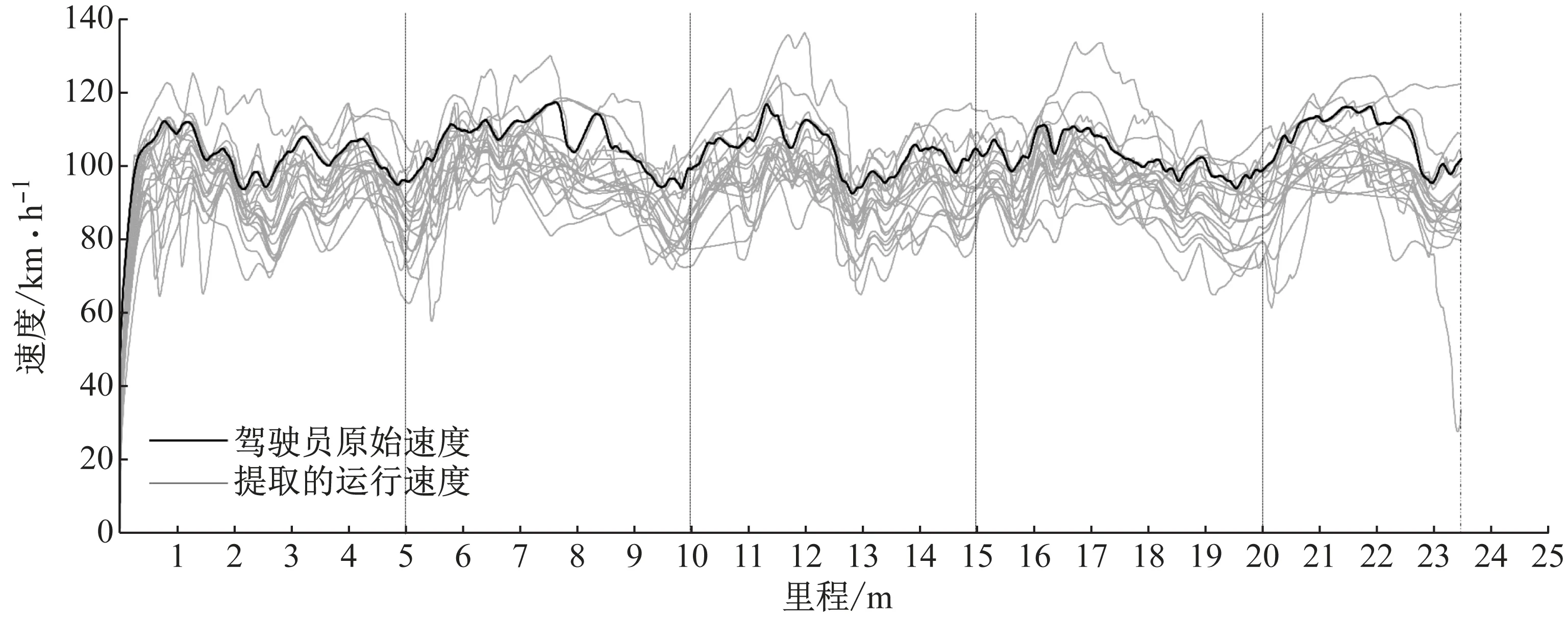
图3 模拟驾驶实验观测运行速度曲线

在实验起始时，驾驶员需要加速至正常行驶速度，而在实验结束前，驾驶员需要按照指示减速停车，因此这两段的数据不适宜用于建模.隧道段速度变化的影响因素复杂，且需要考虑设计形式、照明条件等的差异，因此隧道及洞口前后600 m的数据同样不用于建模分析.本文将里程较长的11 700～19 300路段的数据作为模型训练集，里程较短的500～6 100路段的数据作为测试集，进行建模分析和模型验证.

2 模型构建

2.1 基于特征点的运行速度曲线预测

《公路项目安全性评价规范》及大多数传统研究均采用的是基于特征点的运行速度曲线预测方法.根据规范中给出的运行车速预测模型组和实验道路的设计参数，得到基于规范预测的运行车速曲线，与驾驶模拟实验观测到的运行车速曲线进行对比，如图4所示.从图中可以看到：在实验的起始路段，规范中假定的驾驶员加速的过程较为缓慢，导致预测的运行车速曲线与真实值相差较大；尽管在绝对数值上存在差距，但驾驶员在经过小半径弯道时的加减速行为在两个曲线上有较为相似的反映，如K15—K17路段；在部分路段上，驾驶员真实的车速选择与规范中预测的车速变化有较为明显的差异，集中体现在图中两条曲线大角度相交的位置，如K4—K5路段、K6—K7路段以及K14—K15路段.

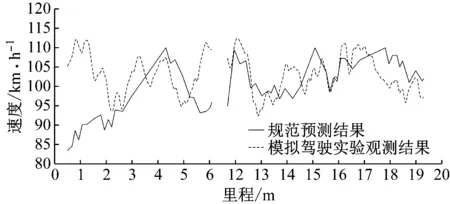
图4 公路项目安全性评价规范预测与模拟驾驶观测运行车速曲线

Fig.4 Highway project safety evaluation specification prediction and simulation driving observation speed curve

以道路3D模型中的驾驶人视角进行检验，两条运行速度曲线差异明显的位置一般为平纵组合路段或连续平曲线路段，通过对比发现：在凹曲线和平曲线组合路段上，驾驶人视距受限，难以判断前方道路线形，即使在圆曲线半径不大的平曲线上也会有明显的减速行为，而规范中弯坡组合路段的车速预测模型会将这种情况预测为驾驶人加速通过；在长度较短的连续平曲线路段上，驾驶人在看到前方曲折的线形后，一般会提前将速度下降到可控的范围内，而规范的模型由于只考虑前方一个路段单元的线形特征，在面对大弯道后接数个小弯道的线形时，预测的减速时机会出现滞后.

在平原地区，道路线形中的平纵曲线分布较为分散，驾驶人行车时的速度选择更多地受当前路段几何设计参数的影响，在应用现有规范进行速度曲线预测时可以有较高的准确度，但在线形特征复杂的山区高速公路，大量的连续平曲线和弯坡组合路段是无法避免的，在这类道路上预测运行速度时，必须考虑上下游邻近的数个路段的线形特征.

2.2 基于上下游设计参数的通用速度预测模型

在线形设计复杂的路段上，路段的特征点，例如直缓点、缓圆点和圆曲线中点等，常常不是路段上车速变化的特征点，很难通过路段划分的方式定位车辆加减速的位置.因此为了准确地描述车速在复杂线形路段上的连续变化情况，本文提出一种针对连续速度数据的通用运行速度预测模型，使用上下游道路设计参数直接预测路段上任意位置的运行速度.该建模方案与以往的特征点速度模型在构建思路上的差异如图5所示.以往的车速建模策略仅预测路段特征点上的运行速度，但通用速度预测模型则使用道路上任意点上下游的几何设计参数作为解释变量进行预测.

图5 速度预测方法差异

影响驾驶员当前位置车速的因素可以从来源上划分为3大类：后方路段线形特征、当前位置属性以及前方路段线形特征.后方路段是驾驶员刚刚行驶过的路段，其线形条件决定了车速的基础值，线形条件越差，速度越低；当前位置属性包括描述曲率、坡度和视距的变量，可以反映驾驶员当前时刻的直接感受；前方路段是驾驶员尚未行驶到的路段，其线形条件决定了驾驶员的车速期望，若线形曲折或即将进入下坡路段，则驾驶员会有减速的倾向.考虑到前后路段线形参数之间的相关性，将前方路段与后方路段的线形参数差值作为模型的解释变量，认为前后线形条件不变时车速保持不变.

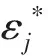
(1)

对通用车速模型而言，简单地使用当前路段的线形参数，如平曲线半径、路段长度等，既不包含点位信息，也不能考虑前后路段的线形特征.为了适应本文提出的通用车速预测模型，模型的解释变量应从各点位上下游的道路设计参数中进行提取.计算当前位置前后路段曲率、坡度、超高、三维视距的最大值、最小值和平均值，统计圆曲线和下坡路段比例，并定义可能影响速度变化的分类变量，如是否存在边坡点、是否为视距受限位置等，作为潜在的模型解释变量.

表1统计的是按照上下游各400 m的距离提取的潜在模型解释变量.其中，平均坡度在计算时考虑上下坡的差异，当路段范围内同时有上坡和下坡时按照距离长短进行加权平均；平均曲率在计算时不考虑左转和右转弯道的差异，反映路段整体的弯曲程度；视距受限变量按照高速公路设计规范中的停车视距要求划分为两类：满足110 m(设计车速为80 km·h-1)视距要求的位置以及视距值小于110 m的位置.

表1 潜在解释变量描述性统计结果(400 m范围)

3 模型结果

3.1 模型参数选择

道路设计参数在前后路段的统计距离对模型结果有显著影响，若统计距离过大，局部明显的几何线形变化可能会被掩盖，反之则会降低速度曲线的连续性.为了选择合适的参数提取距离，通过对比使用不同影响范围(100、200、300、400、500和600 m)的模型的拟合结果，选择拟合度最优的模型对应的影响范围作为最后的变量.结果显示，统计距离为400 m时，使用相同的解释变量，车速回归模型具有更高的调整后，模型具有最优的拟合度，因此取400 m作为最佳的设计参数统计距离.

使用残差图对获得的运行速度多元线性回归模型进行诊断.结果显示，残差服从正态分布，不存在明显的异方差问题，设计参数与运行速度之间存在线性相关关系.使用方差膨胀系数(VIF)对模型进行共线性检验，模型中显著的参数间的方差膨胀系数(VIF)均小于10，说明解释变量之间没有明显的共线性问题.运行车速模型调整后R2为0.74，模型拟合程度较好.

3.2 模型显著变量解释

模型的参数估计结果如表2所示.模型中共有5个显著的解释变量：后方路段平均坡度AvGrd、后方路段平均曲率AvCrv、前后路段平均曲率差DiffCrvAB、后方路段存在反向曲线ChngDir以及后方路段最大超高值MaxSE.

后方路段平均坡度AvGrd：该变量的系数为负值，说明车辆在经过上坡路段后车速降低.从AvGrd系数值的大小可以推断，后方路段的平均坡度每增加1%，当前位置的运行速度将下降1.84 km·h-1.

后方路段平均曲率AvCrv：曲率是半径的倒数，直线段的曲率为零，在缓和曲线段上，曲率由零渐变为圆曲线曲率值，因此曲率与车速之间应为负相关关系.模型中后方路段平均曲率的系数均为负，符合基本推断.根据AvCrv系数可进一步推断：路段平均曲率值每上升1，运行速度将下降2.18 km·h-1.

前后路段平均曲率差DiffCrvAB：该变量系数为负，说明前方的平曲线线形会影响驾驶员当前的车速选择，前方道路越曲折，当前位置的期望车速越低，前后路段平均曲率差为1 km-1时，运行速度降低1.52 km·h-1.

后方路段存在反向曲线ChngDir：当后方路段上存在反向曲线时，变量ChngDir取值为1，其系数为负，说明驾驶员在经过反向曲线时普遍有更明显的减速行为，这一变量对运行速度的影响系数为1.58 km·h-1.

后方路段最大超高值MaxSE：除为了排水而设置的固有横坡，道路横断面的超高一般设置在平曲线上，与线形曲率之间存在较强的相关关系.最大超高值往往与小半径平曲线相对应，其值越大说明线形条件越差.模型中使用的超高单位为百分比，且对不同转向的弯道均以外侧车道的超高值为准进行统计，因此根据模型结果，后方路段的最大超高每上升1%，运行速度将下降1.18 km·h-1.

尽管在选择解释变量时尝试了描述视距的变量，但该变量未能通过显著性检验.可能的原因是实验道路上视距受限的位置较少(受限区间比例不足3%)，大多数位置都满足视距的基本要求.

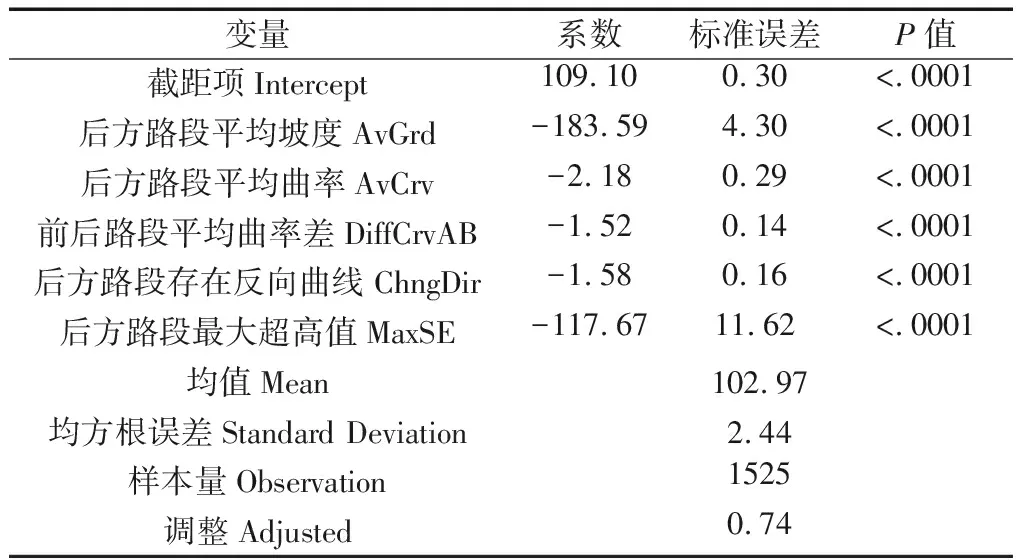
表2 运行速度模型参数估计结果

3.3 模型预测能力

根据线性回归模型的参数，分别预测训练集和测试集路段的运行速度.以均方根误差RMSE、平均绝对误差MAE和平均相对误差MAPE3个指标评价模型的预测结果，指标的计算公式如式(2)、式(3)和式(4)所示，计算结果如表3所示.从表中可以看到，运行速度模型的总体预测性能较好，在训练集和测试集中，模型预测的均方根误差都控制在4 km·h-1以内，平均绝对误差小于3 km·h-1，平均相对误差在3%以内.

(2)

(3)

(4)

表3 运行速度模型预测误差

为了直观反映速度模型的预测能力，绘制驾驶模拟实验中观测的速度曲线和基于通用速度模型预测的速度曲线如图6所示，图中实线为观测的车速曲线，虚线为线性模型的预测结果.预测曲线与实测曲线在车速的总体变化趋势上基本保持一致，在对应的小半径弯道路段上的变化相近，吻合程度高.在实验的起始路段上，预测值与真实值出现了较大的偏差.可能的原因是尽管排除了起始500 m路段的加速过程，但前几公里的路段仍受实验开始阶段的影响，驾驶员较为兴奋，普遍采用了较快的车速.

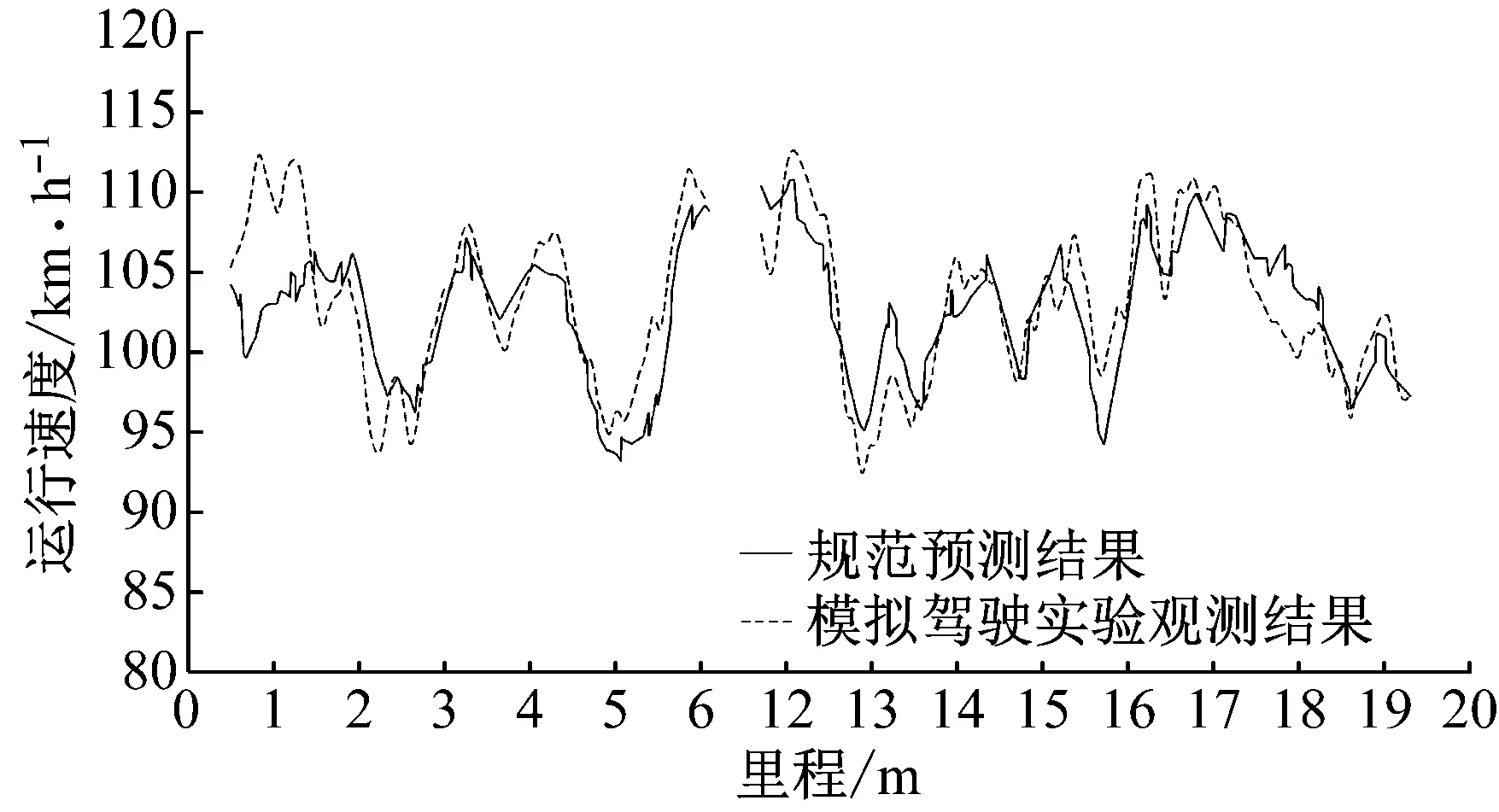
图6 运行速度曲线预测结果

4 结语

速度是道路线形与驾驶行为综合作用的结果，运行车速预测模型则是当前量化评价道路线形设计一致性和安全性的核心.现有的运行车速预测模型一般基于定点断面测速数据构建，难以预测组合线形设计多、线路复杂的的山区高速公路的运行速度曲线.本文基于高仿真驾驶模拟器开展山区高速公路驾驶模拟实验，采集高精度、连续变化的运行速度曲线，以邻近路段的道路线形参数为解释变量，构建了适用于所有位置速度预测的通用模型并测试了模型的预测能力.

实验结果提供了一种有效预测山区高速公路连续车速曲线的建模方案，并为研究驾驶员在复杂线形条件下的车速选择行为提供了基础.由于实验道路隧道数量较少，没有对隧道段进行单独建模，但隧桥作为山区高速公路的重要组成部分，应当在后续的研究中加以考虑.