任意初态下的扰动系统学习控制

李国军，周国民，陈东杰，许中石

（1.浙江警察学院公共基础部，浙江杭州310053；2.浙江警察学院计算机与信息技术系，浙江杭州310053）

学习本是指人们通过阅读、听讲、思考、研究、实践等途径获得知识或技能的过程，目前已被广泛引申到其他领域。控制领域的学习大致可分为三类：单一目标学习,多目标学习以及量化的生物学习。经过研究者的不断努力,学习控制理论体系已日益完善并成为控制方法论中的一个重要分支。学习控制主要包括迭代学习控制和重复学习控制[1]。迭代学习控制(iterative learning control,简称ILC)适用于在有限区间重复作业的场合,利用先前的控制输入和输出产生当前次的输入,以便改进输出效果,经过多次迭代以后,系统能够实现完全无误差跟踪[2-3]。重复学习控制同样着眼于利用受控对象和目标轨迹的周期性或重复性,利用上一周期的输入输出信息来改善当前的控制输入,以期获得理想的输出效果。最大的区别在于迭代学习控制目标是在有限区间上达到完全跟踪,而重复学习控制目标是在无限区间上达到渐近跟踪。由于设计简单、在线计算量小、控制效果好,学习控制被应用于工业机器人控制、化工过程控制等场合。

应用ILC方法时,要求每次的初始定位必须处于某个理想位置,但实际上无法做到。实际应用时只能在某个指定区间实现完全跟踪。在此情形下,可放松对初始定位条件的限制,即每次迭代时的初始状态可不相同。重复学习控制对初始定位操作不作要求,从而回避了迭代学习控制中的初始定位问题,一定程度上推广了重复学习控制的应用范围。

在有初态偏差的情形下,为了实现完全跟踪,研究者做了大量有益的工作[4-22]。目前的解决方法主要分为两类,一类是压缩映射方法,另一类是Lyapunov-like方法。LEE等[9]和PARK等[10]提出了一种基于固定初态误差的修正方法,能在指定区间实现完全跟踪；针对线性连续多智能系统,李国军等[12]提出了一种用step-by-step控制器修正高阶多智能体的初态误差方法,但该方法只能修正固定初态误差,无法修正任意初态误差；LI等[13]提出了一种针对任意初态误差的修正方法,但无法完全修正初始误差,而且只适用于一阶系统。对于相对高阶离散系统,在初态偏差满足某种特定条件下,LI等[14]实现了精确跟踪；对于迭代时变不确定系统,MEMG等[15]实现了有界跟踪。对于任意初态误差的情形,一般采用Lyapunov-like分析方法[16-22]；CHIEN等[18]应用边界层方法达到了渐近跟踪；文献[19-21]利用吸引子达到了实际完全跟踪；YIN等[22]提出了一种离散自适应ILC方法,能确保系统沿着迭代轴渐近收敛、沿着时间轴在指定区间内逐点收敛。

无论是迭代学习控制还是重复学习控制都有自己的优势。但一般的过程控制,既不满足迭代学习控制有限区间重复作业的要求,也不满足重复学习控制中目标轨迹具有周期性或重复性的特点。本文针对任意初态下带有扰动的线性定常系统,利用迭代学习控制的思想,提出了一种新的学习控制算法,该算法将受控过程分成无穷个子过程,不仅可利用上一子过程的输入输出信息来调节当前的输入,而且还可通过初始修正策略获得更快更好的控制效果。该算法系统稳定,且当子过程长度趋向零时,可实现任意小误差跟踪。

1 问题阐述

考虑线性定常系统

其中,t∈ [0,∞ ),x(t)∈Rn,y(t)∈Rr,u(t)∈Rm分别表示系统状态、控制输入和输出向量,ω(t)∈Rn为系统扰动。A,B,C是合适维数的系统参数矩阵，并且B,C可逆。

设yd(t)是给定的期望轨迹，xd(t)是给定的期望状态，e(t)=yd(t)-y(t)表示输出误差。

假设 初始状态x(0)随机，并且状态x(t)可测。

为便于收敛性分析,采用以下形式来描述系统(1)：

其中,t∈[0,h]指有限时间,h为预设的时间常量;k=0,1,2,…,可以理解为迭代次数;xk(t)∈Rn,yk(t)∈Rr,uk(t)∈Rm,ωk(t)∈Rn(相应可以简写为xk,yk,uk,ωk)分别表示系统状态、控制输入、输出和扰动向量。

设yk,d(t)和xk,d(t)(可简写为yk,d和xk,d)分别表示kh+t时刻的期望轨迹和期望状态，ek(t)=yk,d(t)-yk(t)表示kh+t时刻的输出误差。

由系统(2)和系统(1),有

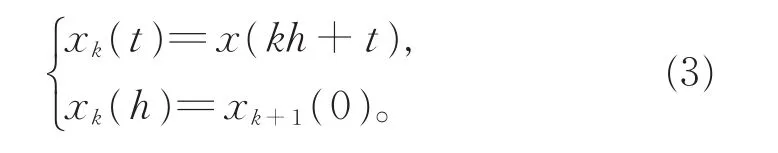
同理,yk(t),yk,d(t),xk,d(t),ωk(t)和ek(t)也具有类似于式(3)的性质。

2 控制器设计

本节的任务是设计一套控制算法,使得系统(2)能跟踪期望轨迹。为此,提出下面的控制律：

其中,

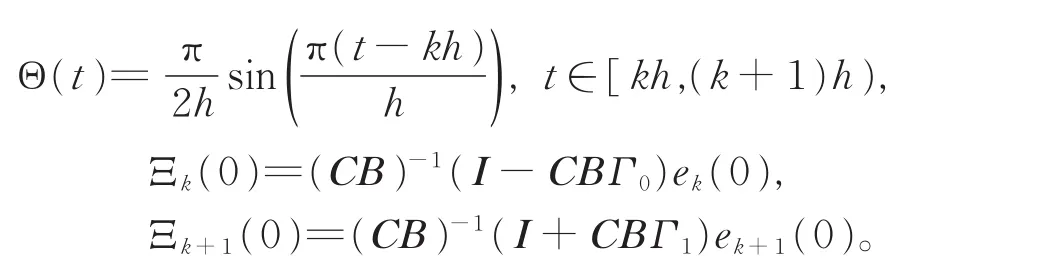
事实上,控制律中的函数Θ(t)并不唯一,但须满足以下性质：

性质对函数Θ(t),有

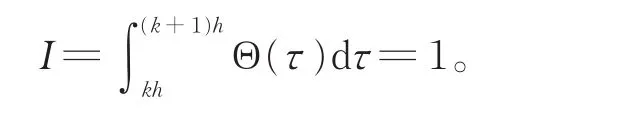
注1此性质表明,Θ(t)函数经过1次积分后具有与脉冲函数类似的作用。而实际中,脉冲函数是不存在的,因此可用此函数代替脉冲函数。

3 收敛性分析

这一节着重分析系统(2)在应用控制律(4)以后的收敛性。上节提出的控制律(4)中,引入了初始修正函数Θ(t),关于初始修正函数有以下定理：

定理如果初始状态是任意有限值,C,B,I+CBΓ1都是可逆矩阵,并且满足

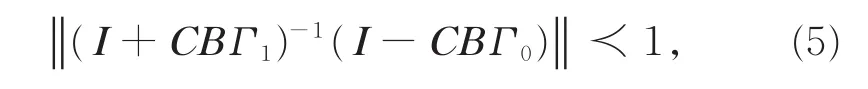
那么，修正控制律(4)能使系统(2)跟踪目标轨迹,并且当k→∞时,跟踪误差可达任意小。

证明为书写方便,记

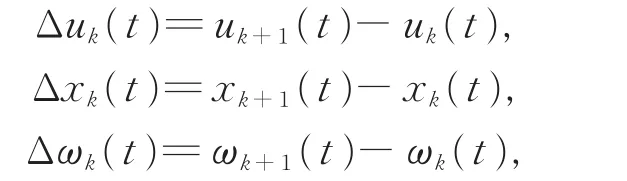
当t∈[kh,(k+1)h)时,可得

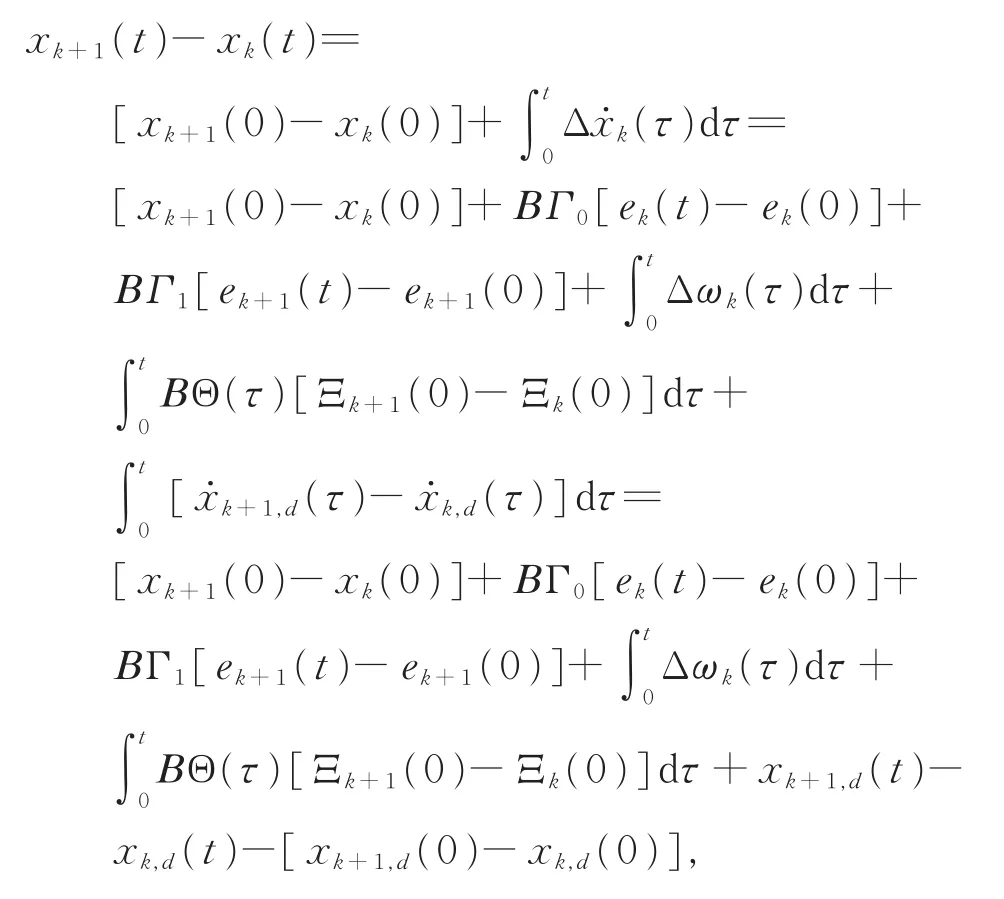
上式两端同乘以矩阵C,整理后可得

代入Ξk(0)和Ξk+1(0)的表达式,进一步化简上式，可得

上式两端同时左乘(I+CBΓ1)-1,可得

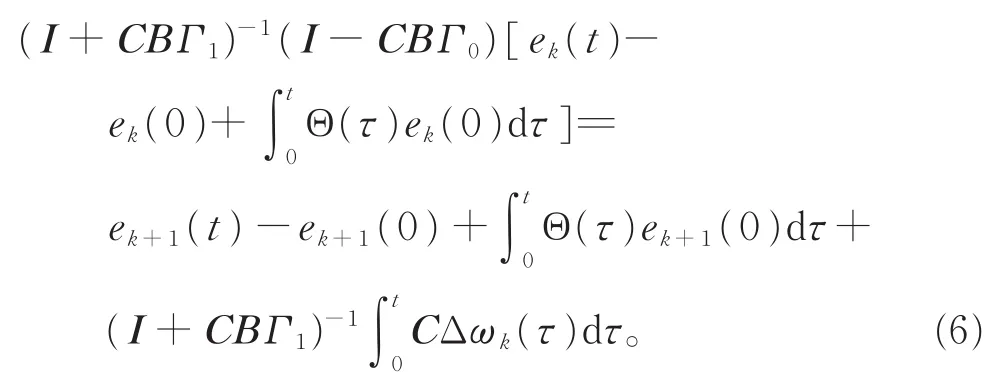
假设轨迹

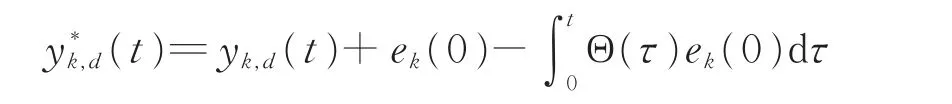
可实现,相应的误差记为e*k(t)=yk*,d(t)-yk(t),而且

由式(6)和(7)得

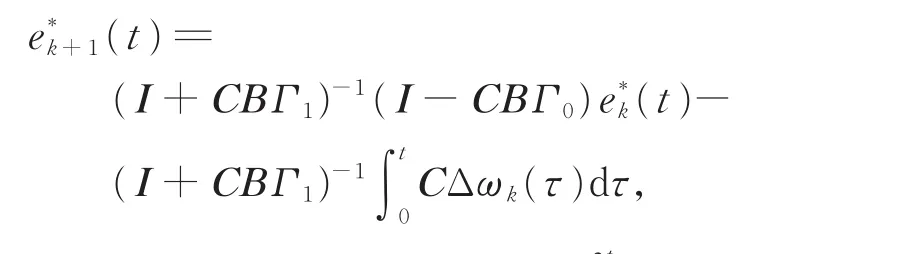
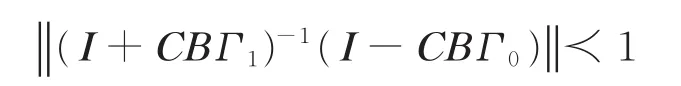
时,有

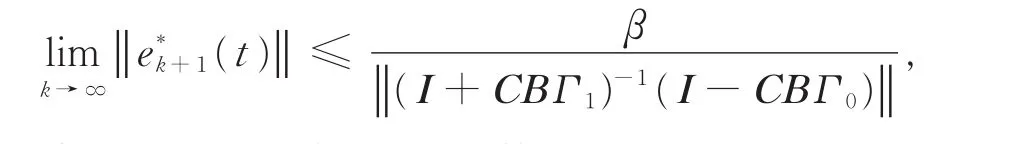
且当t=h时,根据Θ(t)函数的性质有

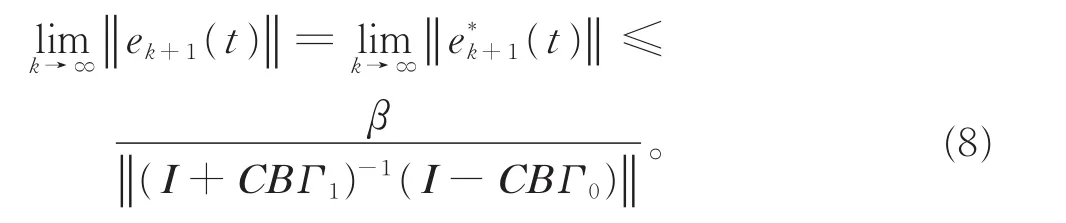
由式(7)有

注2由β的定义知

事实上,如果系统(2)无扰动,只需采用以下控制律即可：

其中,

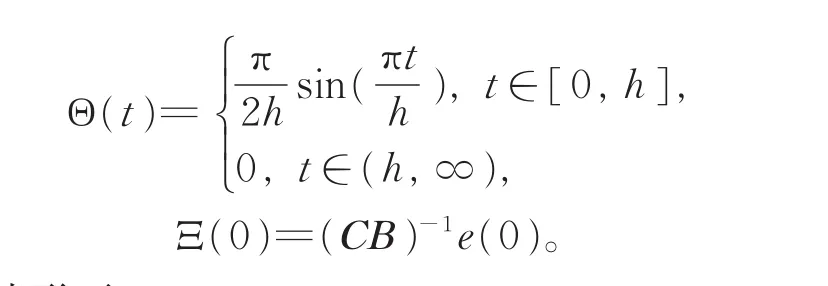
在此情形下,

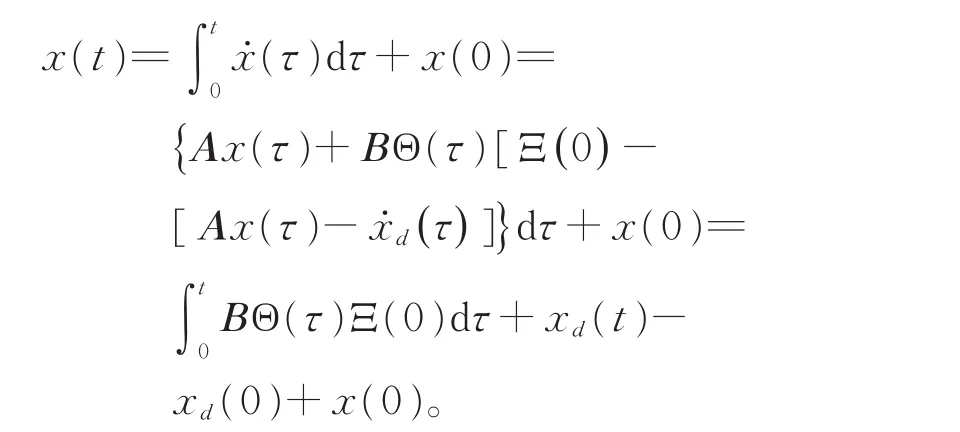
上式两端同乘以C并代入Ξ(0),化简后可得

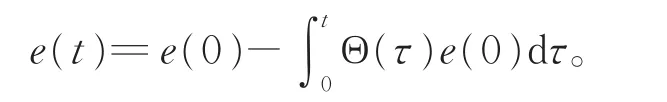
因此,当t≥h时,误差e(t)≡ 0。

4 数值仿真

考虑连续系统

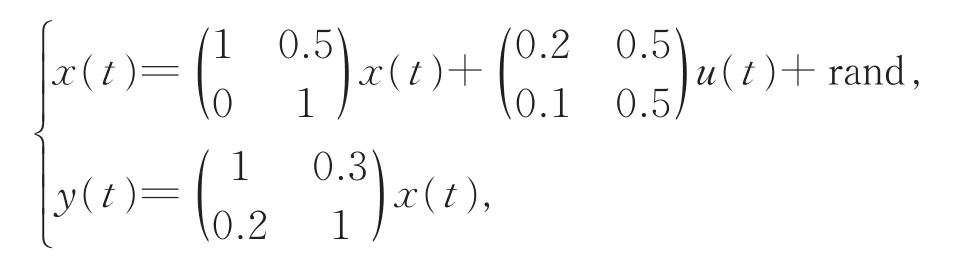
显然,该系统不稳定。其作业区间为[0,20],系统的跟踪轨迹为yd,1(t)=cos(0.1πt),yd,2(t)=sin(0.1πt)。系统扰动为rand(rand表示0～1之间的随机数),系统运行之前的初始状态为x1(0)=0,x2(0)=0。控制增益Γ0=0.8,Γ1=0.8,修正时间h=0.2。仿真结果如图1～图3所示。

图1 期望轨迹yd(t)和实际轨迹y(t)Fig.1 Desired trajectoryyd(t)and actual trajectoryy(t)

从图1和图2中可以看出,系统在初始阶段并未跟踪上目标轨迹,而是经过若干个周期的修正后才实现跟踪，但仍无法达到完全跟踪。

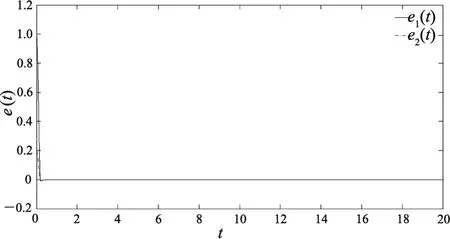
图2 实际跟踪误差e(t)Fig.2 Actual tracking errore(t)

图3 控制量u(t)Fig.3 Actual tracking erroru(t)

从图3中可以看出,系统以0.2为周期不断进行修正,直至误差为零。由于跟踪过程中存在随机扰动,控制器存在轻微颤振。

若系统无扰动,则只需经过1次修正即可达到完全跟踪。

5 结 论

讨论了带有扰动的线性定常系统的学习控制问题,基于迭代学习控制思想,借助压缩映射手段,提出了一种带修正因子的控制策略。对于连续系统,通过不断修正跟踪误差,将误差控制在一定范围,当修正区间长度趋于零时,可实现任意小误差跟踪。特别地,当系统无扰动时,可在指定区间实现完全跟踪。本文从理论和实践两方面验证了算法的有效性。