基于Shannon-Cosine小波精细积分法的壁画降噪修复方法

李丽，高若婉，梅树立，赵海英

（1.中国农业大学信息与电气工程学院，北京100083；2.北京邮电大学世纪学院,北京102613）

中国古代壁画有着辉煌的历史，由原始的岩石壁画，到后来的墓室壁画、石窟壁画、庙堂壁画等，经历了千年岁月的洗礼，具有浓厚的文化与历史色彩[1-2]。古代壁画题材广泛，内容丰富，具有鲜明的民族特色、佛教色彩和民俗风情，每个时期均有其独特的风格，对文化与历史的传承有着十分重要的意义，历来被视为珍宝，具有极高的艺术和学术研究价值[3]。

古代壁画由于长时间受风、日、雨侵袭和一些人为因素的影响，损坏较为严重，不能更好地展示其应有的艺术和欣赏价值。将计算机图像处理技术用于古代壁画的保护，只需要对采集到的壁画图像进行虚拟修复，不需要对壁画本身进行处理，避免了手工修复壁画不可逆的缺点，有效保护原始壁画。因此对壁画进行数字化保护成为一种必然趋势。

受损壁画通常同时存在噪声、模糊、色变等问题，在修复过程中需要重点考虑图像纹理结构的信息，将受损区域按照原有纹理进行修复。

众所周知，图像处理变分理论在生物医学图像处理领域获得了广泛应用，这是因为此类图像具有局部平滑性，而偏微分方程的解本身也具有局部光滑特性，因此，此类图像适合用偏微分方程来描述。壁画不同于自然图像，属于卡通类图像，具有分片光滑特性，且边界分明，轮廓清晰。线性热传导方程无法描述此类图像的边界。因此，非线性偏微分方程法被较广泛地应用于图像处理领域[4-10]。求解非线性偏微分方程最常用的方法是差分迭代法[11]，但数值精度和稳定性以及计算效率仍有待提高。

采用差分法将偏微分方程离散为常微分方程组，每个像素点对应一个常微分方程，规模庞大；对于非线性微分方程，还需要迭代求解，数值计算量巨大[12]。这也是阻碍该方法广泛应用的原因之一。

采用多尺度小波变换理论可对图像进行稀疏表示。利用该理论构造多尺度小波插值算子，对非线性偏微分方程进行离散处理得到的微分方程组，其规模可大大缩减，从而降低该方法的计算量。由上述方法得到的非线性常微分方程组可通过精细积分法求解。精细积分法是一种求解线性常微分方程组的半解析数值方法，无须迭代便可直接得到微分方程组几乎精确的数值解。将其用于非线性常微分方程组求解，可显著减少迭代次数，增大迭代步长，从而提高算法效率[13]。

已有的小波精细积分法大多用Quasi-Shannon小波作为基函数对偏微分方程进行离散。顾名思义，这种拟小波不是真正意义上的小波，且不具备紧支撑性。本文提出将Shannon-Cosine小波精细积分法用于受损壁画的修复，运用Shannon-Cosine小波的多尺度特性，对图像进行小波分解，可以识别图像的纹理和边缘，使处理后的图像轮廓更加突出，纹理更清晰，从而提升壁画的修复效果。相对于拟小波，由于Shannon-Cosine小波具有紧支撑性及小波的所有特性，是真正意义上的小波，具有更高的数值精度和效率。

本文采用非线性偏微分方程法对图像进行描述，利用方程各向异性的特点，实现对图像的保边降噪。针对差分法求解偏微分方程精度低、易使图像产生人工伪影这一问题，本文采用自适应小波精细积分法求解偏微分方程，在保证计算精度的同时，限制偏微分方程离散生成的微分方程组的规模，以提高计算速度，达到对壁画图像降噪修复的目的。

1 基于热传导方程的图像降噪

热传导方程是一种偏微分方程，可将其用于图像降噪。PERONA等[14]提出的P-M模型为扩散偏微分方程，将目标边界和用于追踪封闭轮廓的曲率以及边界和轮廓之间的图像灰度值、梯度值定义为一种能量值，从而建立能量泛函模型：

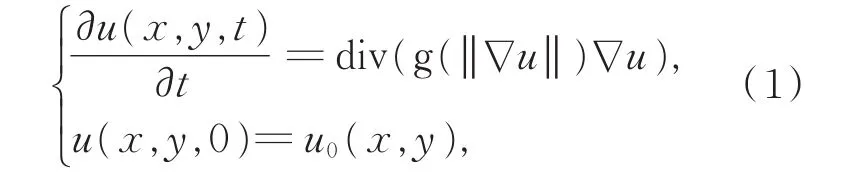
式中，(x,y)表示像素位置，t为时间参数，u0(x,y)为要处理的图像，u(x,y,t)为处理后的图像，简称为u，u(x,y,0)为初始值。div为散度算子，∇为梯度算子为扩散系数。

P-M模型具有各向异性，图像内部和边缘位置的扩散速度不同，在平坦区域，g(‖∇u‖)＞ 0，扩散，图像趋于平滑；在边缘处，g(‖∇u‖)≈ 0，停止扩散，图像不再平滑，进而保护了边缘。其扩散系数函数为

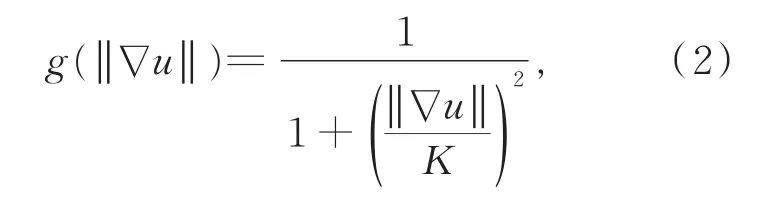
其中梯度阈值为常数。

用热传导方程进行图像降噪时，将待处理图像视为方程（1）的初值，该方程在t时刻的解就是对该图像降噪的结果。求解偏微分方程通常用差分法或有限元法[15]，差分法将定解区域离散化，对于一个固定的点，在该时间步长中，只需要考虑附近的几个点，而不必求所有点。有限元法与差分法特点相同。但以上方法均只是求得近似解，在精度要求高的情况下，因图像中微小细节被忽略，图像处理效果不佳。本文采用Shannon-Cosine小波函数对偏微分方程进行离散，运用小波的多尺度特性，抓住图像纹理特征，可以在图像平滑处稀疏取点，在纹理细节丰富处密集取点，从而有效减少方程组个数，同时保持图像的纹理。

2 小波精细积分法的图像降噪

2.1 Shannon-Cosine小波定义

连续小波变换定义为

由于连续小波是一种卷积运算形式，计算速度慢，故采用插值小波。考虑Shannon类小波是一种插值小波，同时具有正交性、无限次可微等优点，但其支撑区间过大，不满足紧支撑特性，计算速度较慢。

本文采用一种具有紧支撑性的Shannon-Cosine小波[16]，公式为

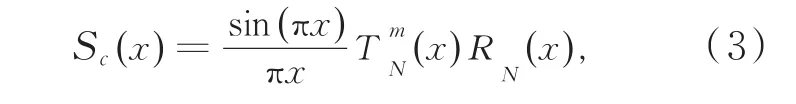
其中，

Shannon函数经过Cosine函数调制，可同时满足正交性、插值性、紧支撑性和连续性等优点，且具有具体的解析表达式，在性能上明显优于Shannon函数。图1为Shannon尺度函数和Shannon-Cosine尺度函数对比图。

2.2 常微分方程的Shannon-Cosine小波空间离散

常微分方程形式为

根据配置法的基本思想，方程（6）的解可近似表示为

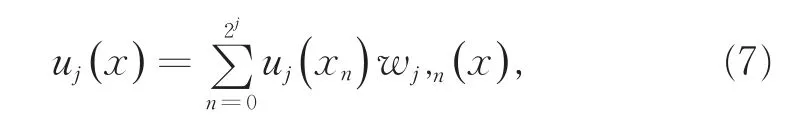
将式（7）代入式（6），可得

图1 Shannon尺度函数和Shannon-Cosine尺度函数的比较Fig.1 Comparison of Shannon scaling functions and Shannon-Cosine scaling functions

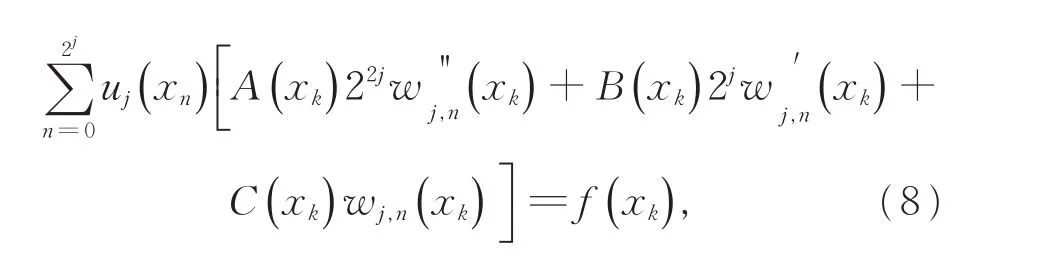
其中，k=0,1,2,…,2j。

如此便将常微分方程转化成线性代数方程组。而该方程组的解，就是常微分方程的近似解。

2.3 二维偏微分方程的小波配置法

设二维偏微分方程为

由配置法思想，偏微分方程的解可近似表示为

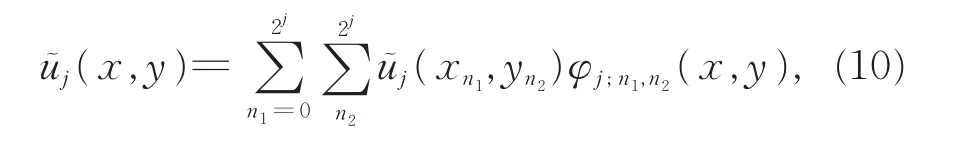
将式（10）代入式（9），可得其小波离散格式为

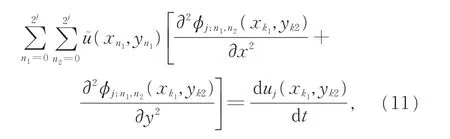
其中，k1=0,1,2,…,2j，k2=0,1,2,…,2j,j∈Z。 记

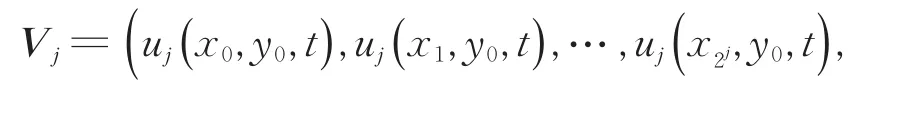
方程组（13）可表示为

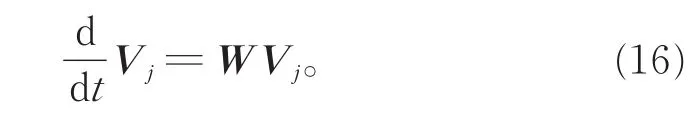
式（16）矩阵的解可表示为

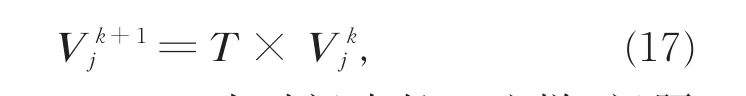
其中，T=exp(M0⋅τ)，τ为时间步长。这样，问题就归结为T矩阵计算。

2.4 非线性常微分方程组的精细积分法求解

钟万勰[17]提出的精细积分法，用于求解线性常微分方程。精细积分法用于计算指数函数exp(Ht)，H为矩阵。该方法首次提出用2N形式而非常用的差分法求解矩阵。可使其在数值上逼近于精确解，且因其可任意选取迭代时间步长，效率很高。

T(τ)的计算利用了加法定理，公式为

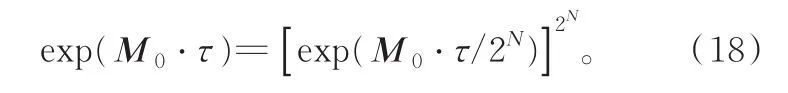
令Δt=τ/2N，N一般取20，由于τ本身就是一个不大的时间步长，因此，τ/2N是一个非常小的区间。其泰勒展开级数为

故矩阵T可表示为

以此重复分解N次，便可求得T矩阵的高精度解。

2.5 算法效率分析

Shannon-Cosine小波精细积分法，在处理图像时可以自适应地选取配置点，且只需对选取的配置点进行处理，可有效提升图像的处理速度。同时，其多尺度特性可以识别图像的纹理特征，令处理后的图像纹理更加清晰。图2（a）为一幅简单的二值图，像素大小为60×60。图2（b）为选取配置点后获得的图像，配置点数为1 044。从图2中可以看出，本算法有效选取了图像的特征点位置，在纹理边缘处密集取点，在平滑处稀疏取点，很好地保留了图像的纹理特征。且算法对图像进行配置点选取后，可明显提升效率。

图2 配置点说明图Fig.2 Explanatory drawing of collocation points

3 算法流程及试验分析

3.1 小波精细积分法的图像降噪步骤

本文算法主要利用偏微分方程模型对彩色壁画图像进行降噪，基本步骤为：首先，读入有损的彩色壁画图像，分为R、G和B通道，依次将3个通道的图像作为模型的输入图像。然后，采用P-M模型对图像进行处理，用Shannon-Cosine小波配置法将偏微分方程组离散成常微分方程组。在该过程中，小波配置法可以自适应地选取特征点，从而有效降低方程组的规模。而后，采用精细积分法求解常微分方程组，得到高精度解。方程组的解即为降噪后图像在该点处的像素值。最后，将偏微分方程模型输出的3个通道的图像合并，得到最终的彩色壁画降噪图像。

3.2 评价指标

3.2.1 峰值信噪比

峰 值 信 噪 比[18]（peak signal to noise ratio，PSNR）用于评价原图像和降噪后图像在像素上的差异。定义为

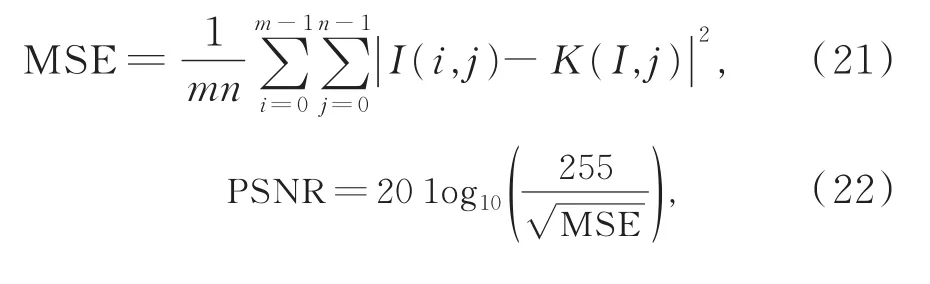
其中，m和n分别表示图像矩阵的行数和列数，i,j∈Z，I和K分别表示降噪后的图像和原图像。

3.2.2 结构相似度

结构相似度（structuralsimilarityimage measurement，SSIM）[19]是评价两幅图像相似程度的指标。值越大，表示两幅图像的结构相似程度越高，最大值为1。计算公式为

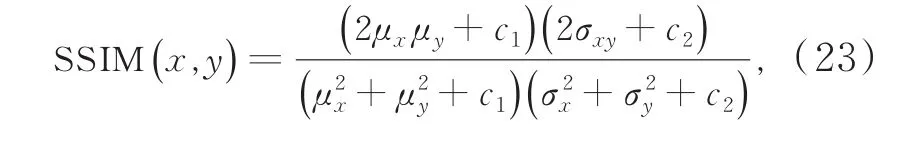
式中，μx和μy表示局部窗口平均值，σxy为协方差，σx2为方差为图像像素值范围。通常情况下，k1=0.01，k2=0.03。

3.3 降噪方法对比分析

此算法以Matlab R2014a作为平台，在Windows 10操作系统上实现。为验证本文算法用于壁画降噪修复的有效性，选用3组壁画进行仿真试验。图3（a）为原始图像，图4（a）为局部放大图。从此2图中可以看出，由于壁画年代久远，墙壁发生损坏，原图像本身所含噪声点较大，颜色分布不均匀，同时图像较模糊。为了从客观指标上对比算法的降噪效果，使用Photoshop软件，手工对原图进行修复，获得了一张清晰度高、比较符合视觉感受的效果图，将其作为评价指标的基准图，如图3（f）所示。

图3 本文算法与其他算法去噪结果对比Fig.3 Comparison of de-noising results between the proposed algorithm and other algorithms

本文算法用P-M模型对壁画进行降噪处理，首先需要选出最佳迭代次数，这里用PSNR和SSIM作为图像评价指标，设定相同的迭代步长进行试验。当迭代次数为25时，PSNR和SSIM均取得最大值，故将迭代次数定为25。

图3为本文算法与中值滤波、均值滤波和维纳滤波方法的降噪效果对比。试验中，中值滤波、均值滤波和维纳滤波方法均采用3×3模板，本文算法迭代次数为25，步长为1。

图4 本文算法与其他算法去噪效果对比Fig.4 Comparison of de-noising results between the proposed algorithm and other algorithms

图5 本文算法与其他算法去噪效果对比Fig.5 Comparison of de-noising results between the proposed algorithm and other algorithms

从图3中可以看出，中值滤波和均值滤波处理后的图像均出现模糊现象，这是因为这2种滤波方法未考虑图像的边界问题，整体降噪时会令边界变模糊。维纳滤波的效果较中值和均值滤波好，但一些噪声点未能通过降噪完全去除，且同样存在边界模糊的问题，图像质量欠佳。本文算法处理后的图像突出了其边界纹理信息，且有效去除了噪声，实现了图像的保边降噪，取得了较好的修复效果。从表1的数据中也可看出，本文算法的PSNR值为32.3067 db，SSIM值为0.909 8，均高于其他算法，所以从客观指标来看，本文算法好于其他算法。

表1 本文算法与其他去噪算法结果的客观评价Table 1 Objective evaluation of de-noising results between proposed algorithm and other algorithms

图6 本文算法与其他算法去噪效果对比Fig.6 Comparison of de-noising results between proposed algorithm and other algorithms

为更好地显示图像细节，图4（a）为从原图中截取的人物手部图像，（b），（c），（f），（e）分别为中值滤波、均值滤波、维纳滤波及本文算法处理效果图。从图中可明显看出，原图像整体噪声较大，墙壁上斑驳的噪声点令图像的视觉效果不佳。中值滤波和均值滤波在降噪的同时使图像边界变模糊，维纳滤波只去除了部分噪声，仍剩有较多噪声点。本文算法总体效果最好，较好地恢复了壁画的纹理特征，有效去除了噪声点。

图5为对图3（a）添加均值为0、标准差为0.01的高斯白噪声后进行的试验。图5（a）为增加噪声后的图像。可以看出，图5（a）噪声点更多，受损程度也更为严重。从图5以及表1中的数据中可以看出，当壁画受损更为严重时，本文算法处理后的图像，在边界保持和去噪效果上均好于另外3种方法。

图6为另外2组壁画的实验效果图，选用3种对比算法中效果最好的维纳滤波为对照图。从图6（a2）中可以看出，经过维纳滤波处理过的图像，人物脸部颜色不够均匀光滑，同时噪声点未得到很好的去除，相较而言，本文算法效果最好。图6（b2）的人物脸部轮廓及衣带上丰富的纹理被过度平滑了，纹理不清晰，本文算法实验效果较好，纹理较清晰。实验数据如表1所示。相较于中值滤波、均值滤波和维纳滤波，本文算法的PSNR值和SSIM值均为最大，也验证了本文算法的可靠性。

4 结 论

采用非线性偏微分方程模型对受损彩色壁画图像进行降噪修复，并用小波精细积分法求解该模型，将实验结果与其他滤波算法结果进行了对比。结果表明，本文算法得到的彩色壁画边界纹理保持较好，同时噪声得到了有效去除，达到了平滑保边的效果。与常见的中值滤波、均值滤波和维纳滤波降噪方法相比，本文算法视觉效果最好，同时其客观评价指标PSNR值和SSIM值均高于另外3种算法，图像纹理结构保持较好。本文算法针对壁画降噪取得了较好的效果。