单株和簇状植物分布方式对消波的影响试验

彭 浩,陈 杰,2,3,蒋昌波,2,3,何 飞,隆院男,2,屈 科, 4,邓 斌,2,4,伍志元,4

(1.长沙理工大学水利工程学院,湖南 长沙 410114; 2.洞庭湖水环境治理与生态修复湖南省重点实验室,湖南 长沙 410114; 3.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114; 4.湖南省环境保护河湖污染控制工程技术中心,湖南 长沙 410114)

波浪冲刷是造成海岸线侵蚀的重要原因之一。近年来,以红树林为代表的近岸水生植物作为一种新型的消波护岸工具,以其消浪效果好、经济成本低且有利于维护海岸生态平衡等特点成为海岸工程关注的焦点[1-2]。

国内外学者关于植物消波特性开展了大量的研究工作。在水动力因素对植物消波的影响方面, John等[3]发现波浪沿沉水植被区传播时,其波高呈指数函数衰减规律,且衰减强度随水深的增加而降低;Tschirky等[4]还提出了植物带透射系数与水动力因素(水深、周期、入射波高)之间的经验公式。大量研究表明,植物的消波特性不仅与水动力因素相关,同时还受植物因素的影响[5-6]。在植物不同组成部位对其消波特性的影响方面,陈杰等[7-8]在研究中采用PVC圆柱模拟刚性植物茎部;Hashim等[9-10]分别探究了刚性植物根部和树冠对波浪传播变形的影响。在植物分布特征对于消波的影响方面,Augustin等[11-13]通过试验研究发现,植物分布密度越大,其消波效果越好。然而,对于同一植被区域,即使植物分布密度相同,植物仍可呈现不同的分布排列结构,进而产生不同的消波特性。目前关于分布方式对植物消波影响的研究较少。同时,海岸植物在人类活动和生态环境的影响下常以簇的形式分布[14],现阶段对于以簇状存在的植物消波特性研究较为罕见。

为弥补现有研究的不足,拟通过物理模型试验,研究单株和簇状形式下分布排列结构对植物消波特性的影响。

1 理论分析

1.1 植物带密度和排列结构定义

Nepf[15]基于圆柱概化模型提出以单位流域面积内植物投影面积p定义植物密度:

(1)

式中:N0为单位面积的植物株数;D为植物直径;S为植物间距;h为水深。由式(1)进一步推出表征植物密度的无量纲参数pd:

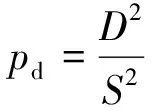
(2)

虽然式(2)忽略了植物形状与摆动效应,但为探索植被密度对水流阻力的影响提供了较为合理的依据[15-16]。

图1 植物尾涡区消波

图1为植物尾涡区消波示意图，展示了由于植物存在产生的紊流区和尾涡区,以及植物排列结构产生的尾涡遮蔽区和尾涡重叠区。当植物间横向间距小于紊流区与尾涡区长度之和或植物尾涡区发生纵向重叠时,植物间将产生遮蔽效应或重叠效应,使得植物的消波能力减弱[15-17]。

在现阶段学者研究中大多数采用的矩形分布[7-8]、交错分布[8,11,18-20]、随机分布[21]3种植物分布方式中,Nepf[15]给出了交错分布植物带的排列结构定义式:

(3)

式中:n为植物排列结构参数;L1为植物间纵向(垂直于水流方向)间距;L2为植物间横向(沿水流方向)间距。

1.2 植物拖曳力系数计算模型

现实情况下,海洋波浪具有较强的随机性,常采用不规则波进行植物消浪的相关研究[11,18-20]。Mendez等[22]提出了不规则波的植物消波解析模型,并给出了波能衰减系数εv的表达式:

(4)

式中:CD为拖曳力系数,表征植物带在微观尺度上的消波效果[23];bv为单株植物迎水面宽度;k为波数;α为植物淹没度;hv为植物高度;arms为不规则波波幅。

也可用式(4)求解植物的拖曳力系数CD。前人研究发现植物的拖曳力系数CD与邱卡数Kc、植物淹没度α之间存在密切联系,为便于分析,定义植物淹没度为

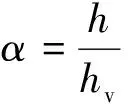
(5)

定义邱卡数Kc来表征植物所受拖曳力对惯性力的相对值:

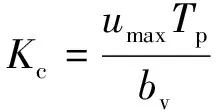
(6)

式中:Tp为周期;bv为单株植物迎水面宽度;umax为静水面处水质点水平最大速度,采用线性波理论求得[2,22]:

(7)

式中:a为入射波振幅。

同时,定义植物带透射系数Kt来表征植物带在宏观尺度上的消波效果[23]:

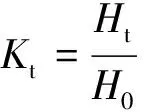
(8)

式中:Ht为植物带后方的透射波高;H0为植物带前方的入射波高。

在前人的研究基础上,结合Yang等[14]关于簇状植物的试验研究,开展试验模型设计。利用式(4)求得单株-交错分布植物拖曳力系数,并与相关学者[11,18-20]的研究成果进行整合,采用式(8)计算单株-矩形分布植物带以及簇状-矩形和簇状-交错植物带透射系数,并得到植物带透射系数与水动力因素和植物因素之间的关系式。

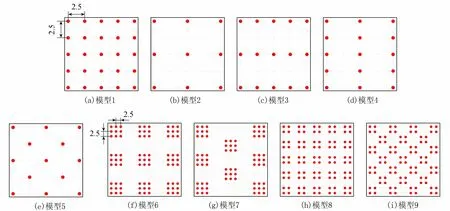
图3 植物模型分布方式(单位：cm)

2 试验布置

试验在长沙理工大学长40.0 m、宽0.5 m、高0.8 m的波浪水槽中进行。水槽前端的液压伺服式造波机可产生规则波和不规则波,水槽末端铺设有由多孔介质材料组成的消能网,以减小波浪反射的影响(图2)。

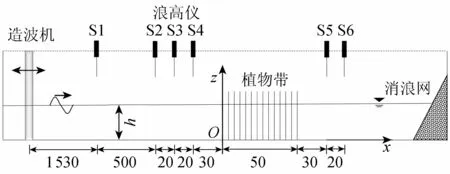
图2 试验布置(单位:cm)

在何飞等[5-6,24-25]的试验研究基础上,同时考虑设备条件的限制,确定试验几何比尺为1∶20。采用PVC圆管概化模拟刚性植物,其弹性模量E=2.9 GPa,与波浪相互作用时不会产生明显的变形[26]。采用高hv=45 cm、直径D=1.0 cm的PVC圆管模拟树龄为15 a、树干直径为20 cm左右的红树林。试验时将 PVC管插置在有机玻璃底板上,底板尺寸为50 cm×48 cm×1.6 cm,孔间距为2.5 cm。坐标原点与造波板的距离为21.0 m,模拟植物布置在x=0.0～50.0 cm的位置。

设计矩形和交错两种分布方式,并分别采用单株和簇状两种植被结构特征,探讨不同分布方式下排列结构对植物消波特性的影响。利用式(2)进行单株-交错植物带密度计算,参考式(2)重定义单株-矩形植物带密度参数gd和簇状植物带密度参数ψ分别为

(9)

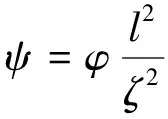
(10)

式中:l为簇直径;ζ为簇中心间距;φ为单簇植物固体体积分数;V为控制体体积;VS为控制体中植被固体所占体积。

在非淹没条件下,植物淹没高度与水深相等,植物固体体积分数可以用植物投影面积总和与植物带面积的比值进行计算。

共设计9种红树林的分布模型,其中模型1～4为单株-矩形分布,模型5为单株-交错分布,模型6和模型8为簇状-矩形分布,模型7和模型9为簇状-交错分布(图3)。具体试验模型参数如表1所示,水波参数的设置如表2所示(表中T为规则波周期,H为规则波波高,Tp为不规则波谱峰周期,Hrms为不规则波均方根波高),共进行22组次试验。

试验时首先放置植物模型,随后对造波机预热,保证造波机性能稳定,开启数据采集系统,确保浪高仪性能良好。然后调整水槽中水位至试验水位,待水面平静后开始造波,使用6个加拿大WG-50型浪高仪测量沿程波高,其数据由江苏东华测试技术有限公司开发的DH5922动态信号测试分析系统采集。浪高仪最小测量周期为1.5 μs,误差为0.4%,采样频率为50 Hz,规则波数据采集时间不少于60 s,不规则波数据采集时间不少于3 min。完成一个组次试验后,需待水面平静后,再进行下一组次的造波,重复上述步骤完成所有组次试验。

表1 模型参数

表2 试验水波参数

3 结果分析与讨论

3.1 单株形式植物

近岸植物影响下的波浪传播变形规律复杂,其主要影响因素有水动力因素(水深、波长、周期和入射波高等)和植物因素(植物带长度、植物分布排列结构、植物分布密度等)[5-6]。单株-矩形分布植物带透射系数Kt可表示为

f(h,H,L,T,B,D,L1,L2,n,Kt)=0

(11)

式中:L为波长;B为植物带长度。式(11)可变为如下形式:

(12)

式中:ak为波陡;kh为相对水深。

建立单株-矩形分布植物带透射系数与波陡、相对水深、植物带相对长度、植物分布密度、植物排列结构参数之间的关系式,规则波与不规则波的拟合度分别为0.924和0.780,可综合反映出水动力因素及植物因素对单株-矩形分布植物带消波特性的影响。具体拟合情况如图4所示。

规则波

(kh)0.179(ak)-0.155

(13)

不规则波

(kh)0.118(armsk)-0.064

(14)

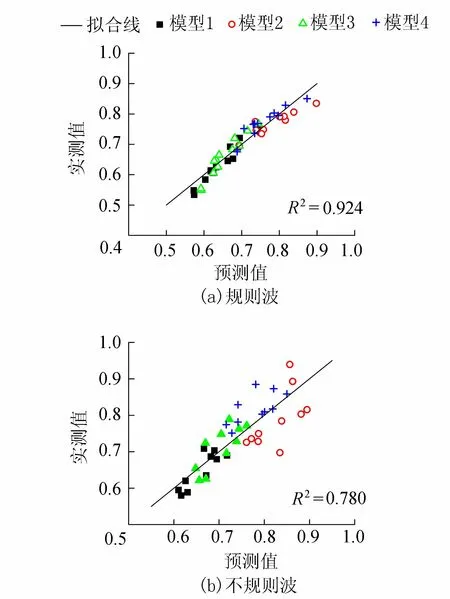
图4 单株-矩形分布植物带透射系数Kt预测值与实测值对比

结合Augistin等[11]、Hu等[18]、Wu等[19-20]在不规则波作用下交错分布植物消浪特性研究中的相关数据,建立不规则波情况下单株-交错分布植物带拖曳力系数与邱卡数、植物带密度参数、植物排列结构参数、植物淹没度之间的关系式,拟合度为0.858(式(15),图5)。

CD=7.726Kc-0.577pd-0.439S-0.775α0.154

(15)

图5 不规则波作用下单株-交错分布植物拖曳力系数CD预测值与实测值对比

3.2 簇状形式植物

受水动力因素和植物因素共同作用,簇状植物带透射系数可用下式表示:

f(h,H,L,B,D,l,m,ζ,Kt)=0

(16)

式(16)可变为如下形式:

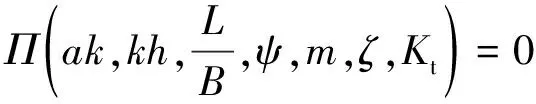
(17)

分别建立不同波况下簇状-矩形分布(式(18)(19),图6)和簇状-交错分布(式(20)(21),图7)植物带透射系数与波陡、相对水深、植物带相对长度、植物带密度参数、单簇内植物株数、簇中心间距的关系式,拟合度分别为0.880、0.796、0.920和0.620。

簇状-矩形分布规则波

ζ0.444(kh)0.128(ak)-0.098

(18)

簇状-矩形分布不规则波

ζ0.254(kh)0.009(armsk)-0.078

(19)

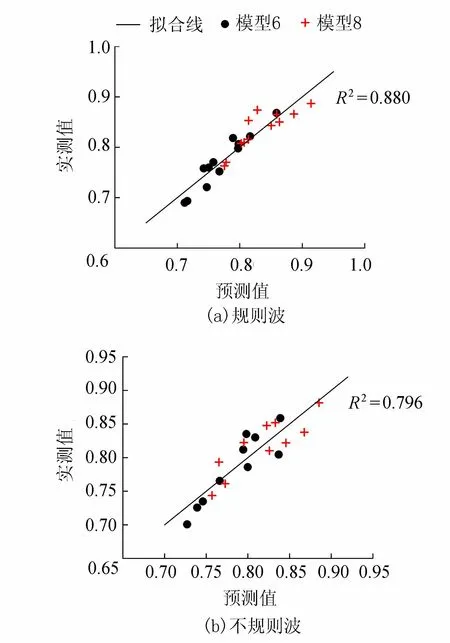
图6 簇状-矩形分布植物带透射系数Kt预测值与实测值对比

图7 簇状-交错分布植物带透射系数Kt预测值与实测值对比

簇状-交错分布规则波

ζ0.230(kh)0.149(ak)-0.113

(20)

簇状-交错分布不规则波

ζ0.350(kh)0.069(armsk)-0.134

(21)

3.3 拟合公式检验与讨论

为了定量考察经验公式预测值与实测数据的吻合情况,引入均方根偏差RM的变异系数CV:

(22)

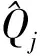
受水动力因素和植物因素的共同影响,植物消波特性变化非常复杂,造成部分数据点与拟合曲线偏差较大,但从整体上看仍呈幂函数关系。假设D=1 cm,由式(13)～(15)以及式(18)～(21)可以预测本试验没有开展的部分工况结果。

表3 实测数据与经验公式预测值均方根偏差的变异系数

图8为规则波和不规则波作用下单株-矩形分布植物n从0.25增大至3以及gd从0.09增大至0.465的理论计算结果。由图8可知,gd相同时,Kt随n的增大而增大,当n介于0.50和2之间时,Kt对n的敏感度较大。当gd从0.09增大至0.35时,Kt迅速减小,gd大于0.35时,Kt对gd的敏感度较小,植物的消波效果趋于稳定。综上所述,在单株-矩形分布方式下,当gd相同时,适当增加相邻植物间沿流向的距离,植物间遮蔽效应减弱,消波效果增强；当n相同时,适当减小植物间的横向和纵向间距,植物的消波阻力效应增强。

图8 单株-矩形分布植物带透射系数Kt与植物带密度、排列结构之间的关系

图9 单株-交错分布植物拖曳力系数与邱卡数、植物间距及植物淹没度之间的关系

图9为不规则波作用下单株-交错分布植物带S从4 cm增大至24 cm、α从0.1增大至1.0及Kc均从10增大至100的理论计算结果。从图9(a)可见,CD随S的增大而增大,当S从8 cm增大至12 cm时,CD对S的敏感度较大,当S>12 cm时,CD对S的敏感度较小。从图9(b)可知,在非淹没情况下,CD随α的增大而增大,即植物消波能力随α的增大而增强。此外,邱卡数Kc从10增大至70过程中,拖曳力系数CD迅速减小,当Kc从70增大至100期间,CD对Kc的敏感度逐渐降低。综上所述,在单株-交错分布方式下,CD随Kc的增大而减小,且CD对Kc的敏感度随Kc的增大而降低。同时,在本试验条件下,CD随α及S的增大而增大,适当增大S,植物间遮蔽效应和重叠效应减弱,植物带消波效果增强。

图10(a)(b)分别为不同波况下簇状-矩形分布植物ζ从10 cm增大至20 cm和ζ从10 cm增大至17 cm,单簇内植物株数m从4株增加至9株的理论计算结果,图10(c)(d)分别为不同波况下簇状-交错分布植物ζ从10 cm增大至20 cm以及ζ从10 cm增大至17 cm,m从4株增加至9株的理论计算结果。从图10可知,当ζ相等时,Kt随m的增加而减小,当4

图10 簇状植物带透射系数与簇中心间距、单簇内植物株数之间的关系

4 结 论

a. 红树林的存在可以抵挡波浪对岸线的冲刷,起到保护岸线的作用。对于单株-矩形分布植物带,gd从0.09增大至0.35时,Kt迅速减小；当gd大于0.35时,Kt对gd的敏感度较小,植物带消波效果趋于稳定；当gd相同时,适当增加相邻植物间沿流向的距离,消波效果增强。对于单株-交错分布植物带,CD随S以及α增大而增大,且当S从8 cm增大至12 cm时,CD对S的敏感度较大；当S>12 cm时,CD对S的敏感度较小。

b. 对于簇状植物带,在各分布方式下均出现随着m的增加以及ζ的减小,波浪通过植物带衰减越剧烈的现象,同时,Kt对m的敏感度在47后逐渐降低。适当增加m及减小ζ,植物带的消波效果增强。

c. 在试验条件下,得到了植物带消波效果与水动力因素和植物因素之间的关系式,重点讨论了植物分布密度和排列结构对植物消波的影响,有助于完善生物海岸的水动力学理论,为采用近岸植物护岸提供一定的理论依据。