基于分层自主学习的改进粒子群优化算法

袁小平 蒋硕

摘 要：针对粒子群优化（PSO）算法容易陷入局部最优、收敛精度不高、收敛速度较慢的问题，提出一种基于分层自主学习的改进粒子群优化（HCPSO）算法。首先，根据粒子适应度值和迭代次数将种群动态地划分为三个不同阶层;然后，根据不同阶层粒子特性，分别采用局部学习模型、标准学习模型以及全局学习模型，增加粒子多样性，反映出个体差异的认知对算法性能的影响，提高算法的收敛速度和收敛精度;最后，将HCPSO算法与PSO算法、自适应多子群粒子群优化（PSO-SMS）算法以及动态多子群粒子群优化（DMS-PSO）算法分别在6个典型的测试函数上进行对比仿真实验。仿真结果表明，HCPSO算法的收敛速度和收敛精度相对给出的对比算法均有明显提升，并且算法执行时间和基本PSO算法执行时间差距在0.001量级内，在不增加算法复杂度的情况下算法性能更高。

关键词：群体智能;粒子群优化算法;粒子差异性;种群多样性;自主学习

中图分类号： TP301.6; TP18

文献标志码：A

Abstract： Focusing on the shortages of easily falling into local optimal， low convergence accuracy and slow convergence speed in Particle Swarm Optimization （PSO） algorithm， an improved Particle Swarm Optimization based on HierarChical autonomous learning （HCPSO） algorithm was proposed. Firstly， according to the particle fitness value and the number of iterations， the population was dynamically divided into three different classes. Then， according to characteristics of different classes of particles， local learning model， standard learning model and global learning model were respectively adopted to increase particle diversity and reflect the effect of individual difference cognition on performance of algorithm and improve the convergence speed and convergence precision of algorithm. Finally， HCPSO algorithm was compared with PSO algorithm， Self-adaptive Multi-Swarm PSO algorithm （PSO-SMS） and Dynamic Multi-Swarm PSO （DMS-PSO） algorithm on 6 typical test functions respectively. The simulation results show that the convergence speed and convergence accuracy of HCPSO algorithm are obviously higher than these of the given algorithms， and the execution time difference of the proposed algorithm and basic PSO algorithm is within 0.001 orders of magnitude. The performance of the proposed algorithm is improved without increasing complexity.

Key words： group intelligence; Particle Swarm Optimization （PSO） algorithm; particle difference; population diversity; autonomous learning

0 引言

群體智能算法是通过观察动物群体的捕食、迁徙等活动，进行仿真模拟而产生的智能算法，粒子群优化（Particle Swarm Optimization， PSO）算法是Kennedy等[1]在1995年提出的一种基于种群的智能算法。PSO算法是定义于连续空间的群智能算法，具有参数较少、原理简单、并行搜索和全局收敛等优点，已经广泛应用于永磁电机关键参数调整[2-3]、人脸识别[4]、分配优化问题[5]等相关领域;但是，PSO算法也存在收敛精度不足、搜索速度较慢以及容易早熟收敛等缺点。针对这些问题，研究人员通过引入相关理论改进学习模型、改变参数调整方式、引入学习算子、算法融合以及多子群等方法对基本算法进行改进研究。文献[6]引入混沌量子理论改进PSO算法理论模型，结合高效局部搜索机制和自适应动态惩罚方法进行约束处理，提高求解精度，并用之于优化问题中。文献[7]使用策略协同机制，引入反向学习、高斯变异和柯西分布等概念，改进PSO算法理论模型，提高算法收敛精度。文献[8]采用自适应惯性权重调整方式，平衡算法的全局和局部搜索能力，提高算法的优化性能，但是惯性权重调整方式对算法的性能提高有限。文献[9]中提出多惯性权重的调整方式调整惯性权重提高算法的性能，但是算法稳定性较差。文献[10]改进PSO算法中的学习因子，变化学习因子的取值，提高速度更新和学习过程，并通过实验验证取得一定的效果。文献[11]通过动态速度修改和引入免疫学习算子对算法进行改进，并将改进算法应用于电机参数估计，优化系统参数估计模型取得较好效果。文献[12]通过模糊高斯学习策略构建精英粒子群进化融合机制，提高种群多样性与收敛性，增强算法逃离局部最优位置的能力。文献[13]通过将PSO算法和混合教学算法进行融合互补，弥补算法全局搜索能力不足的问题，取得一定效果，但是将算法复杂化。文献[14]首次提出多子群策略优化算法性能，为算法改进提供了新思路。文献[14]首次提出多子群策略优化算法性能，为算法改进提供了新思路。文献[15]进一步对多子群策略进行研究，提出动态多子群粒子群优化（Dynamic Multi-Swarm Particle Swarm Optimization， DMS-PSO）算法，优化效果较为突出。文献[16]以自主学习和精英群策略对多子群PSO算法进行改进，提高算法收敛精度，缩短寻优时间。文献[17]将遗传算法和多子群算法进行融合，变换子群的更新方式，加强算法在全局搜索和局部搜索之间的平衡能力，提升算法性能，取得一定的效果。文献[18]将种群分为精英亚群和几个正常亚群并通过一组基准函数进行测试验证了算法的收敛速度和全局收敛能力，并应用于永磁同步电机参数估计，取得较好效果。

上述研究中对PSO算法的理论模型、重要参数设置以及算法融合方面的改进都能在一定程度上提高PSO算法的性能，但本质上依然未解决提升PSO算法的收敛精度和搜索速度之间的矛盾问题，多子群策略虽然能够取得较好的效果，但是依然存在分群过程中粒子数量过多、计算量巨大以及粒子学习过程中学习模式固定、缺乏自主独立性等问题。

基于此，以分级策略作为切入点，通过类似多子群的方式，提出基于分层自主学习的改进粒子群优化（Particle Swarm Optimization based on HierarChical autonomous learning， HCPSO）算法，对种群进行动态分层，在不增加种群粒子数量的情况下，根据不同阶层粒子特性采用不同的学习模型，提高粒子学习的自主性，反映出个体差异和认知对其进化的影响，以中间层实现粒子间的信息交流，随着算法迭代动态调整粒子学习模型，提高算法性能。

1 基本粒子群算法

基本PSO算法的数学描述如下。

粒子群的初始种群规模设定为N，粒子维数为n维，在t时刻粒子i在解空间的坐标定义为Xti=（xti1，xti2，…，xtin），i=1，2，…，N，其速度大小决定了粒子每次在解空间飞行距离大小，用Vti=（vti1，vti2，…，vtin）表示，则粒子i在时刻t的第j（j=1，2，…，n）维空间中的速度以及位置更新公式如式（1）～（3）所示：

其中：ω为惯性权值;c1和c2为加速因子;r1和r2是在[0，1]区间内的两个随机数，粒子在解空间进行搜索的过程中，粒子的速度会被限定在一个最大搜索范围之内，速度最大值用vmax表示，限定粒子在搜索过程中的范围，改善算法性能。gbest为全局极值，而pij表示个体极值。

2 HCPSO算法

2.1 HCPSO算法原理

在基本PSO算法中，种群中所有粒子都是单纯地按照式（1）和（3）更新，使得种群在收敛时，降低了多样性，导致算法容易陷入局部最优。有研究表明，在寻优过程中较优粒子会有更大概率靠近最优位置，而较差粒子更偏离最优位置[18]，因此，本文根据粒子适应度值和函数评价次数将种群动态划分为三个不同阶层，对不同阶层的粒子采用不同的学习方式。这种分级策略在增加种群多样性的同时，一定程度上提高了粒子的搜索速度。上层粒子较优，其邻域内存在更好解的可能性更大，因此对其采用局部学习模型，加强局部范围搜索能力;中层粒子处于优劣之间，作为整个群体信息交流的桥梁，兼顾全局与局部搜索能力，保留基本学习模型;下层粒子较差，因此让其以一定概率随机游走，并采用全局学习模型，增强种群多样性。

算法迭代初期，种群中大部分粒子距离最优位置较远，因此使上层粒子较少、下层粒子较多，增强算法全局搜索能力;算法迭代后期，粒子逐渐向最优位置靠拢，需对解空间进行细致搜索，因此增加上级阶层粒子，同时减少下级阶层粒子，加强算法局部搜索能力，提高收敛速度。隨着算法迭代，各阶层粒子的数量变化如图1所示。

2.2 HCPSO算法具体实现过程

PSO算法优化过程中，设当代全体粒子适应度值大小用集合F={f1， f2，…， fN}表示，其中：N代表粒子总数， fi代表的是第i个粒子适应度值大小。根据适应度值大小对全体粒子进行升序排列（此处适应度值越小代表粒子位置越优），形成新的粒子序列集合X={x1，x2，…，xN}，重新排序后粒子的序号唯一标识粒子的优劣程度，如图2所示。

由图2可知，重新排序后，粒子序号越大，表示粒子适应度值越差，因此，将重新排序后的粒子序号作为划分粒子为不同阶层的依据。设定全局最优粒子重新排序后的序号为NXl，low和up分别表示分层的下界和上界，具体更新方式如式（4）和（5）所示：

3.2 实验设置

实验硬件环境为Intel Core i5-4258U CPU @ 2.40GHz，内存为8GB，在Matlab 2017a下完成。

为增强可比性，选择多子群方面的改进算法来进行对比仿真实验，选取基本PSO算法、DMS-PSO算法、PSO-SMS（Self-adaptive Multi-Swarm PSO）[19]算法与HCPSO算法进行仿真对比实验，统计适应度误差均值与标准差，算法各自独立运行50此处为50次，而3.4节中却是30次，不一致，是写错了，还是我们理解错了？请明确。回复：那个实验是两次实验，分开的，也可以理解成我重复了两次实验，但是第二次实验独立运行次数只进行了30次。第一次实验独立运行了50次，这个没有写错。次。不同的PSO设置了统一参数。算法参数设置为：ω=0.7296，最大迭代次数T=2000，学习因子c1=c2=2，粒子维数分别取10维和30维，其他对比算法的特定参数选取如参考文献所述，此处不再赘述。

3.3 算法收敛情况分析

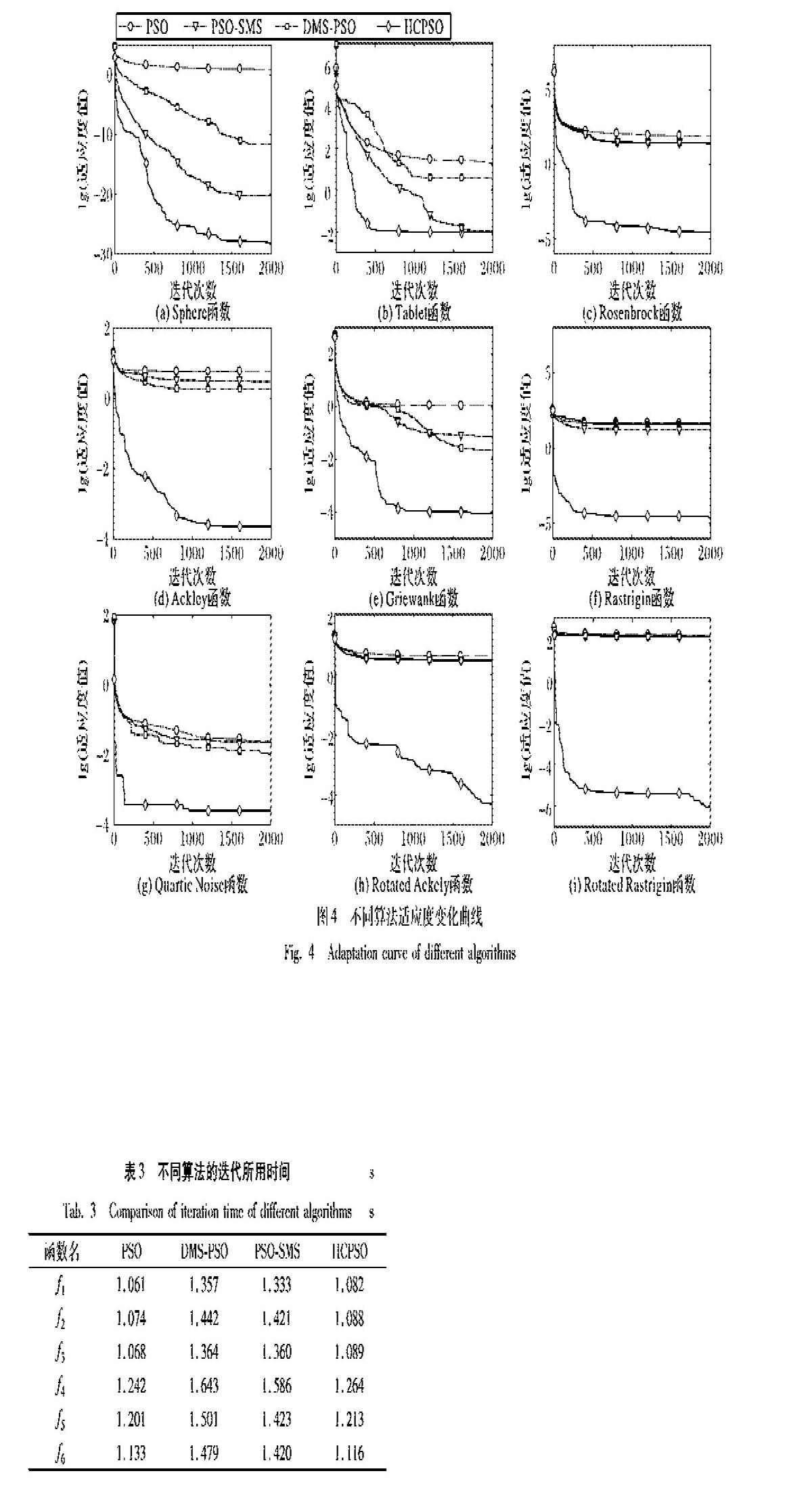
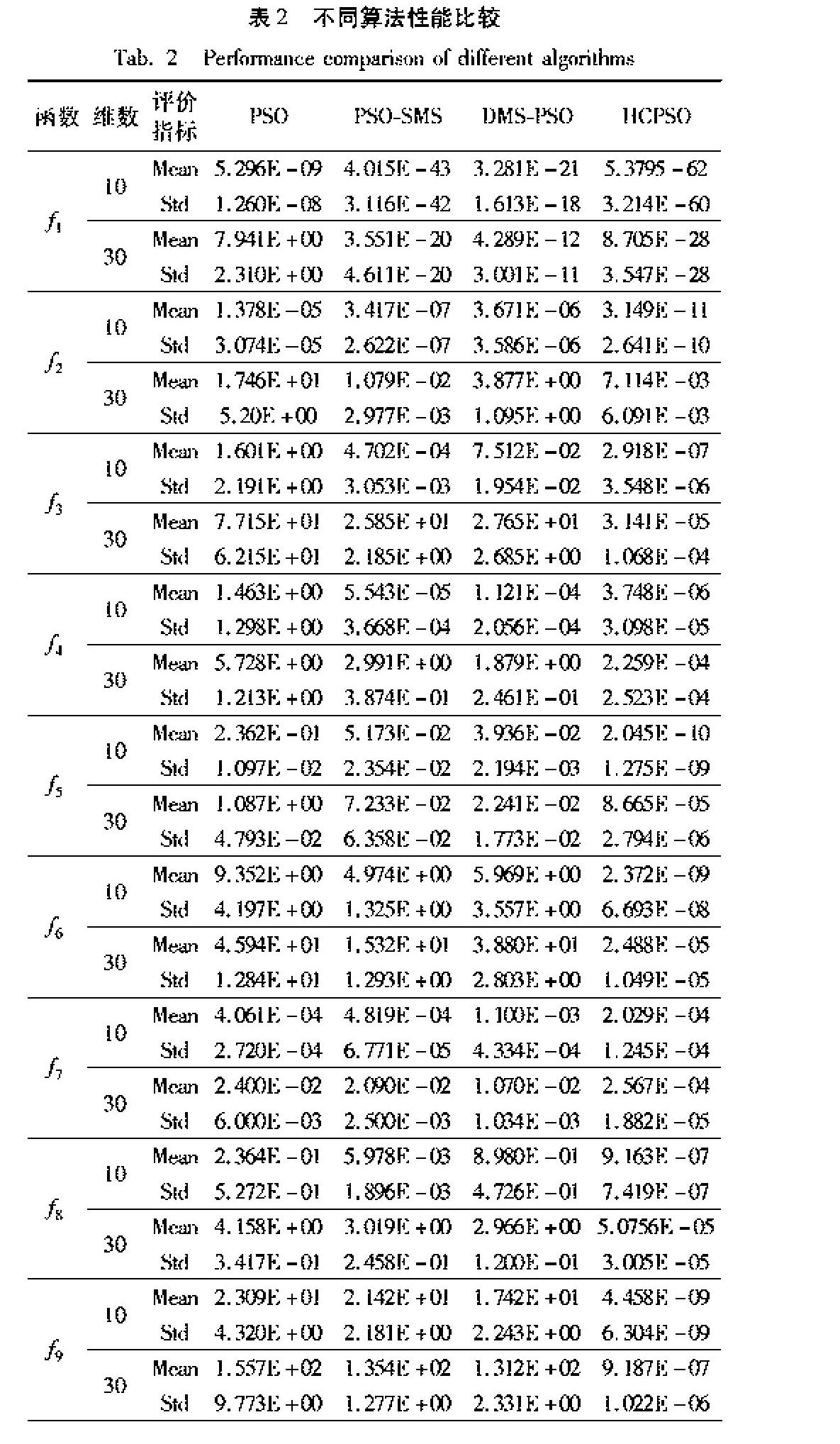
表2给出了4种算法在6个标准测试函数上的粒子平均适应度（Mean）和标准差（Std）的统计对比数据，粒子分别取10维和30维。

由表2中数据可以看出，不管对单峰函数、多峰函数、噪声函数还是旋转多峰函数，HCPSO算法相对于基本PSO算法和其他两种对比算法在收敛精度和稳定性上都有较为明显的优势。函数1～3均为单峰函数，由统计数据可以看出，对于函数1～2几种算法都能取得一定的优化效果，但是HCPSO算法的优化精度明显更高，稳定性也更好，函数3是相对更为复杂的单峰函数，由表中可以看出其他对比算法优化效果较差，而HCPSO算法依然可以保持较好的优化效果;函数4～6均为多峰函数，由表2中统计数据可以看出，针对多峰函数，HCPSO算法依然有较高的收敛精度，PSO算法很快就陷入局部最优，PSO-SMS算法以及DMS-PSO算法在10维的时候能够取得一定的优化效果，但是随着维数增加，其优化效果变得较差，而HCPSO算法随着维度的增加，收敛精度波动较小，证明HCSPO算法对于高维多峰问题有较好的适应性，对于多峰函数，HCPSO算法收敛精度较高，证明下层粒子按照全局学习模型以及扰动方式更新可以增加粒子多样性，提高算法前期的全局搜索能力，让粒子在搜索过程中更容易跳出局部最优位置，找到更好的解;函数7为噪声函数，由表2中的统计数据可以看出，在10维的时候HCPSO算法的优化效果较好，基本PSO算法的优化效果次之，而PSO-SMS算法和DMS-PSO算法优化效果较差，可以看出HCPSO算法抗干扰能力较好，随着维度的增加，PSO-SMS算法和DMS-PSO算法的抗干扰能力相对有所提升，但是和HCPSO算法相比依然有较大差距;函数8～9为典型的旋转多峰函数，由表2中的数据可以看出，不管实在10维还是30维的情况下HCPSO算法相对其他对比算法都有明显的优势，特别是对函数9优势较大。

为了更直观地表现出算法在迭代过程中的收敛情况，图4给出了粒子维数取30维的情况下，各算法在不同测试函数上的优化对比曲线，纵坐标是以10为底取对数后的结果。在算法迭代初期，保持下层粒子较多，粒子更容易跳出局部最优位置，找到更好的解，由图4中（a）、（c）、（e）、（g）和（h）可以看出，算法在迭代过程中有明显跳出局部最优的过程，证明下层粒子的扰动和更新策略的有效性。上层粒子随着算法迭代的进行，粒子数逐渐增加，由图中曲线的变化趋势可以看出，HCPSO算法的收敛速度对比其他算法有明显提高，证明上层粒子进行局部搜索能够在一定程度上加快算法后期收敛，验证了改进策略的有效性。

3.4 算法复杂度分析

如表3所示，给出了4种算法在6个测试函数上独立运行30次，平均每次所需的时间（计算机性能对时间影响较大），粒子维数为30维，最大迭代次数为2000。

由表3可以看出，在相同的迭代次数下，基本PSO算法迭代所用时间最短，DMS-PSO算法由于分群原因，其粒子数较多，运行时间相对增加，而PSO-SMS算法虽然分群过程中各子群的粒子较少，但是需要对粒子进行多次重组增加了运行时间，HCSPO算法所需时间对比基本PSO算法差别并不明显，由此可以看出所提出的改进策略并没有以消耗运行时间为代价来提高算法的性能。

由基本PSO算法的执行流程可以看出，算法的时间复杂度主要来自于粒子位置初始化以及粒子速度和位置更新部分，其时间复杂度均可以表示为O（N·D）。对2.3节中HCPSO算法伪代码的描述进行分析，得出算法在运行过程中增加了对粒子所在层级的判断，需要按照适应度值的大小对粒子进行排序，排序部分时间复杂度表示为O（N2），在粒子维数较小时，维度大小近似和种群规模相同，而实际情况中，粒子维度取值一般比较适中，所以HCPSO算法的时间复杂度近似记为O（N·D），并未在数量级上改变算法的复杂度。

4 结语

本文对PSO算法的原理进行了深入分析研究，针对基本PSO算法易陷入局部最优、收敛精度不高、收敛速度较慢的问题，提出一种基于分层自主学习的改进PSO算法。首次提出类似多子群方式的分层方式，通过对种群进行动态分层，根据不同层级粒子特性采用不同的学习模型，增加粒子多样性和自主学习能力，让算法更容易跳出局部最优位置。动态分层方式可以在不增加粒子数的情况下实现类似分群的效果，并且中间层作为通信桥梁避免了粒子信息交流过程中通信周期难以确定的问题。最后通过仿真实验验证了改进策略的有效性。然而本文算法存在有待改进之处，例如中级阶层粒子数较多，对算法的影响较大，基本学习模型还有进一步改进优化空间，并且将算法在实际问题中进行验证，将理论应用于实际有待深入讨论，这将是下一步需要研究的问题。

參考文献 （References）

[1] KENNEDY J， EBERHART R. Particle swarm optimization[C]// Proceedings of the 1995 IEEE International Conference on Neural Networks. Piscataway， NJ： IEEE， 1995：1942-1948.

[2] LIU Z H， WEI H L， LI X H， et al. Global identification of electrical and mechanical parameters in PMSM drive based on dynamic self-learning PSO [J]. IEEE Transactions on Power Electronics， 2018， 33（12）： 10858-10871.

[3] LIU Z H， WEI H L， ZHONG Q C， et al. Parameter estimation for VSI-Fed PMSM based on a dynamic PSO with learning strategies [J]. IEEE Transactions on Power Electronics， 2017， 32（4）： 3154-3165.

[4] MISTRY K， ZHANG L， NEOH S C， et al. A micro-GA embedded PSO feature selection approach to intelligent facial emotion recognition [J]. IEEE Transactions on Cybernetics， 2017， 47（6）： 1496-1509.

[5] GHAMRY K A， KAMEL M A， ZHANG Y. Multiple UAVs in forest fire fighting mission using particle swarm optimization[C]// Proceedings of the 2017 International Conference on Unmanned Aircraft Systems. Piscataway， NJ： IEEE， 2017： 1404-1409.

[6] TURGUT O E. Hybrid chaotic quantum behaved particle swarm optimization algorithm for thermal design of plate fin heat exchangers [J]. Applied Mathematical Modelling， 2016， 40（1）：50-69.

[7] 李俊，汪冲，李波，等.基于多策略协同作用的粒子群优化算法[J].计算机应用，2016，36（3）：681-686.（LI J， WANG C， LI B， et al. Particle swarm optimization algorithm based on multi-strategy cooperation [J]. Journal of Computer Applications， 2016， 36（3）：681-686.）

[8] ZHANG L， TANG Y， HUA C， et al. A new particle swarm optimization algorithm with adaptive inertia weight based on Bayesian techniques [J]. Applied Soft Computing， 2015， 28（C）：138-149.

[9] GUPTA I K， CHOUBEY A， CHOUBEY S. Particle swarm optimization with selective multiple inertia weights[C]// Proceedings of the 2017 International Conference on Computing， Communication and Networking Technologies. Washington， DC： IEEE Computer Society， 2017：1-6.

[10] ZHOU Z， JIAO B. The improvement of particle swarm optimization[C]// Proceedings of the 2017 International Conference on Systems and Informatics. Piscataway， NJ： IEEE， 2017： 373-377.

[11] LIU J， MEI Y， LI X. An analysis of the inertia weight parameter for binary particle swarm optimization [J]. IEEE Transactions on Evolutionary Computation， 2016， 20（5）：666-681.

[12] 周偉，罗建军，靳锴，等.基于模糊高斯学习策略的粒子群进化融合算法[J].计算机应用，2017，37（9）：2536-2540.（ZHOU W， LUO J J， JIN K， et al. Evolutionary algorithm for particle swarm optimization based on fuzzy Gauss learning strategy [J]. Journal of Computer Applications， 2017， 37（9）：2536-2540.）

[13] WANG H， LI Y. Hybrid teaching-learning-based PSO for trajectory optimization [J]. Electronics Letters， 2017， 53（12）：777-779.

[14] LOVBJERG M， RASMUSSEN T K， KRINK T. Hybrid particle swarm optimiser with breeding and subpopulations[C]// GECCO01： Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation. San Francisco： Morgan Kaufmann， 2001：469-476.

[15] LIANG J J， SUGANTHAN P N. Dynamic multi-swarm particle swarm optimizer [C]// Proceedings of the 2005 IEEE International Swarm Intelligence Symposium. Piscataway， NJ： IEEE， 2005：124-129.

[16] 姜海燕，王芳芳，郭小清，等.基于自主学习和精英群的多子群粒子群算法[J].控制与决策，2014，29（11）：2034-2040.（JIANG H Y， WANG F F， GUO X Q， et al. Multi-swarm particle swarm optimization based on autonomic learning and elite swarm [J]. Control and Decision， 2014，29（11）：2034-2040.）

[17] 金敏，鲁华祥.一种遗传算法与粒子群优化的多子群分层混合算法[J].控制理论与应用，2013，30（10）：1231-1238. （JIN M， LU H X. A multi-subgroup hierarchical hybrid of genetic algorithm and particle swarm optimization [J]. Control Theory and Applications， 2013，30（10）：1231-1238.）

[18] 郭文忠.离散粒子群优化算法及其应用[M].北京：清华大学出版社，2012：46-46.（GUO W Z. Discrete Particle Swarm Optimization Algorithm and Its Application [M]. Beijing：Tsinghua University Press， 2012：46-46.）

[19] 曾辉，王倩，夏学文，等.基于自适应多种群的粒子群优化算法[J].计算机工程与应用，2018，54（10）：59-65.（ZENG H， WANG Q， XIA X W， et al. Particle swarm optimization algorithm based on self-adaptive multi-swarm [J]. Computer Engineering and Applications， 2018，54（10）：59-65.）