基于粒子群优化和支持向量机的花粉浓度预测模型

赵文芳 王京丽 尚敏 刘亚楠

摘 要：为了提高花粉浓度预报的准确率，解决现有花粉浓度预报准确率不高的问题，提出了一种基于粒子群优化（PSO）算法和支持向量机（SVM）的花粉浓度预报模型。首先，综合考虑气温、气温日较差、相对湿度、降水量、风力、日照时数等多种气象要素，选择与花粉浓度相关性较强的气象要素构成特征向量;其次，利用特征向量与花粉浓度数据建立SVM预测模型，并使用PSO算法找出最优参数;然后利用最优参数优化花粉浓度预测模型;最后，使用優化后的模型对花粉未来24h浓度进行预测，并与未优化的SVM、多元线性回归法（MLR）、反向神经网络（BPNN）作对比。此外使用优化后的模型对某市南郊观象台和密云两个站点进行逐日花粉浓度预测。实验结果表明，相比其他预报方法，所提方法能有效提高花粉浓度未来24h预测精度，并具有较高的泛化能力。

关键词：花粉浓度;支持向量机;粒子群优化算法;Spark;花粉浓度预测

中图分类号： TP391; TP181

文献标志码：A

Abstract： To improve the accuracy of pollen concentration forecast and resolve low accuracy of current pollen concentration forecast model， a model for daily pollen concentration forecasting based on Particle Swarm Optimization （PSO） algorithm and Support Vector Machine （SVM） was proposed. Firstly， the feature vector extraction was carried out by using correlation analysis technique to select meteorological data with strong correlation with pollen concentration， such as temperature， daily temperature difference， relative humidity， precipitation， wind， sunshine hours. Secondly， an SVM prediction model based on this vector and pollen concentration observation data was established. The PSO algorithm was designed to optimize the parameters in SVM algorithm， and then the optimal parameters were used to construct daily pollen concentration prediction model. Finally， the forecast of pollen concentration in 24 hours in advance was made by using the optimized SVM model. The comparison among the accuracy of the optimized SVM model， Multiple Linear Regression （MLR） model and Back Propagation Neural Network （BPNN） model was performed to evaluate their performances. In addition， the optimized model was also applied for the forecast of pollen concentration in 24 hours in advance at Nanjiao and Miyun meteorological observation stations. The experimental results show that the proposed method performs better than MLR and BPNN methods. Meanwhile， it also provides promising results for forecast of pollen concentration in 24 hours in advance and also has good generalization ability.

Key words： pollen concentration; Support Vector Machine （SVM）; Particle Swarm Optimization （PSO） algorithm; Spark; pollen concentration forecast

0 引言

花粉过敏已经成为季节性的流行疾病，具有相当高的发病率。北京作为人口密集的超大城市，花粉过敏病患者占呼吸道过敏病患者的比例已超1/3，在花粉高峰期间大约有几十万人以不同程度的发病，所需花费的医疗费用相当可观。参照1%的发病率来计算，如果每位患者根据花粉浓度预报信息采取了防护措施，每年可节约医疗费用300元，按服务效益30%计算，北京每年可至少节约900万元。通过准确的花粉预测服务，提醒花粉敏感者提前采取有效的预防和医疗措施，减轻花粉过敏的发病症状，是花粉气象服务、环境气象服务和医疗气象服务的重要宗旨[1]，因此，建立和发展精细准确的花粉浓度预报是一项既重要又迫切的工作，同时也具有很高的经济和社会效益。

目前花粉浓度预报主要使用统计学预报法，即选择对花粉浓度有影响的气象因素作相关性分析，然后建立多元线性回归模型进行预测[2-3]。白玉荣等[4-5]曾作过天津气象要素与花粉浓度的相关性分析，并以温度作为主要气象因子建立了逐日花粉浓度预报方程;张德山等[6-9]应用正交筛选多元回归方法建立预报方程作北京地区的花粉浓度预报;这些研究取得了一定的成果并应用在花粉预报日常业务中，但实际的预报效果不尽如人意。首先，气象因素与花粉浓度并非線性的关系，它对花粉的影响十分复杂，同一气象要素在植物生长的不同阶段影响差异很大，而目前的实际预报并没有根据植物的不同物候期具体分析，导致预报的花粉浓度存在较大不确定性。其次，这些研究工作在花粉观测业务建立的初期就已经完成，但由于当时数据来源有限，数据规模较小，无法全面分析花粉浓度的影响因素，导致模型预测值往往偏离实际观测值;然而在当前，机器学习的智能算法可以处理大量的历史和当前花粉浓度数据和气象数据，从而更准确地建立预测模型。

支持向量机（Support Vector Machine， SVM）是一种常用于模式识别、分类和回归分析的监督学习模型。近年来，SVM在小样本、非线性、高维模式识别等问题的解决上表现出许多特有优势，可避免神经网络中经常出现的过拟合及局部极小等问题，推广误差较小，具有较好的泛化能力，已经被广泛用于解决一些回归问题。本文提出将支持向量机与粒子群优化（Particle Swarm Optimization， PSO）算法相结合的方法，首先利用皮尔逊算法找出与花粉浓度相关的气象要素并进行特征提取，再结合支持向量机算法进行建模并使用粒子群算法对模型进行优化，进而得到花粉浓度预报结果，有利于降低不确定影响因素对预测结果的影响，也为花粉浓度预报提供一种新方法。

1 相关工作

对于预测模型，SVM能较好地解决非线性问题，近年来也被广泛应用在PM2.5浓度预报、大气污染等级预报等预报领域。李龙等[10]选择综合气象指数、二氧化硫浓度、一氧化硫浓度、二氧化氮浓度和PM10浓度构成特征向量，利用特征向量和PM2.5浓度数据应用最小二乘支持向量机（Least Squares Support Vector Machine， LS-SVM）预测模型。结果表明，该模型能更准确地预测PM2.5浓度，具有较强的泛化能力;刘杰等[11]提出应用SVM和模糊粒化时间序列相结合预测PM2.5的方法，结果表明这种预报模型可以较好解决PM2.5机理性建模方式下由于影响因素考虑不全而造成的预报结果不稳定的问题;岳鹏程等[12]提出应用SVM和模糊粒化时间序列相结合的方法预测公路SO2浓度，结果表明这种算法不受机理性理论研究的限制，支持小样本学习，非线性拟合效果好，泛化能力强;陈柳等[13]提出了大气污染物浓度的小波分析及支持向量机时间序列预测模型。

以上研究表明，已有大量文献利用支持向量机结合模糊粒化、小波分析等应用在PM2.5浓度预测、大气污染预测和SO2浓度预测中，但是将支持向量机应用至花粉浓预报中的研究相对甚少。本文提出一种将支持向量机与粒子群优化算法相结合的花粉浓度预测模型。

2 数据预处理与分析

2.1 花粉浓度的时间序列分析

以2013—2017年北京地区7个观测站点在花粉观测期（每年4—9月）的逐日花粉监测样本为数据基础，分析花粉浓度的季节性周期变化规律。花粉浓度观测方法如下：采用医院常用的镜检用片，在长76mm、宽22mm的载玻片上均匀地涂上一层凡士林，将该载物片放到室外花粉采集架上，空气中的部分花粉就会落到载玻片上，24h后取回载物片，进行染色，在显微镜下读取花粉颗粒数。花粉浓度就是指花粉在空气中24h内每千平方毫米沉降的颗粒数。

北京地区的花粉含量随季节变化明显，高峰为春季和秋季，春季多为木本花粉，秋季以草本花粉为主。图1反映了北京地区2013—2017年同期4—9月的逐日花粉浓度随时间的变化趋势，横坐标为4月1日—9月30日共183天，纵坐标为逐日花粉浓度，可以看出春季4—5月、秋季8—9月各有一个高峰，受每年同期气象条件差异影响，花粉浓度高峰出现的时间也存在差异。

2.2 花粉浓度与气象要素的相关性分析

气象因素对花粉浓度的影响十分复杂，往往是不同气象因素相互影响的结果。如果分别考虑各个因素，则不能很好体现多个因素相互作用对花粉浓度产生的耦合效应，从而影响预报模型的准确性。本文综合考虑平均气温、最高气温、最低气温、气温日较差、平均相对湿度、降水量、平均气压、平均风速、最大风速、日照时数等多种气象因素数据，选择可靠的相关性分析方法对气象因素与花粉浓度进行分析，最后选择相关性较强的因素构成特征向量。

通过收集整理，建立了7个观测站逐年4—9月的逐日花粉浓度和11个气象要素的数据样本集，共计5310个样本。利用Spark并行计算框架的机器学习库，编写程序并在大数据环境下运行，快速分析出花粉浓度与各气象要素相关性，如图2所示。从图2可以看出：平均风速、气温日较差、日照时数、平均相对湿度、平均气压与花粉浓度呈现正相关;平均气温、最大气温、最低气温、极大风速、日降水量、最大相对湿度与花粉浓度呈负相关;其中平均气温、最大气温、最低气温、气温日较差与花粉浓度相关性较强，相关系数绝对值大于0.4。

3 花粉浓度预测模型

SVM是在研究统计学习理论基础上提出的分类设计准则。粒子群优化算法是一种进化计算技术，其基本思想是通过群体中个体之间的信息传递及信息共享来寻找最优解。在SVM建模过程中，如何确定最优参数值是建模的关键，已有优化方法主要有网格搜索法、遗传算法、粒子群算法、蚁群算法等。网格搜索法是一种穷举搜索算法，参数优化时间相当长;遗传算法具有较强的搜索能力，但是自身参数设置缺乏理论指导;粒子群算法比遗传算法简单，比蚁群算法搜索速度更快。本文以花粉浓度观测数据和多个气象要素作为基础数据，结合SVM和粒子群算法建立花粉浓度预测模型。

本章主要介绍相关的算法和模型。

3.1 非线性ε-支持向量机回归

利用SVM进行非线性回归和预测是将数据非线性映射到高维特征空间，然后在该特征空间建立线性模型来拟合回归函数。核函数常用来解决数据的非线性映射问题，大量的实验和研究表明，采用径向基函数（Radial Basis Function， RBF）为核函数具有较高的拟合和预测精度，故通常选用其作为核函数进行研究[14-16]。损失函数是评价预测准确程度的一种度量，ε不敏感损失函数是其中一种，通过将松弛变量ξ引入支持向量机，采用ε不敏感损失函数进行样本训练，得到非线性ε-支持向量回归。松弛变量ξ度量了训练样本点上误差的代价，在ε不敏感带内的点误差为0。

1）初始化粒子群算法系列参数。设置粒子的数目等于30，优化过程的结束条件为粒子迭代次数达到设定值100。

2）每个粒子的位置用向量（C，γ），初始化30个粒子的位置和加速度。

3）设置适应度函数为模型预测结果的均方误差。根据每个微粒值的大小即（C，γ）代入SVM重建回归模型，根据检验样本的计算结果和式（9）即可得到每个微粒对应的适应值。对30个粒子的适应值进行比较，适应值最小的那个粒子的值将其记为前群体的最优位置。

4）开始迭代计算。根据式（6）更新所有粒子加速度，根据式（7）更新所有粒子的当前位置;重复第3）步，计算更新后的每个粒子的适应值。将当前粒子群中取得的最小适应值与前几代粒子群优化取得的最小适应值进行比较，择最小值作为前群体最优位置，最小值对应的粒子（C，γ）作为最优参数。

5）达到迭代次数结束计算过程。

3.4 花粉浓度预测模型

基于北京市气象局2013—2017年逐年4—9月的花粉实况观测浓度、花粉预报浓度和主要的气象因素等资料，联合应用SVM和具有自适应惯性权重的粒子群算法建立花粉浓度预测模型，对未来24h浓度进行预报。在实验之前，首先将所有数据进行预处理，计算每类数据的均值和方差，根据均值和方差相互关系的基本规律，将均值在缩小而偏差在增大的数据看作错误数据，并从样本集中剔除。

本方案首先选用皮尔逊相关系数算法得出各气象要素和花粉浓度的相关性，然后选择相关系数大于0.2的气象要素、花粉浓度观测数据、花粉浓度预报数据组成特征向量建立SVM模型，再利用粒子群算法优化SVM的惩罚参数和核函数参数得出最终预测模型。模型流程如图3所示，具体步骤如下：

1）对所有数据进行预处理，计算均值和方差，剔除掉明显错误的数据样本。

2）使用皮尔逊系数计算各气象要素与花粉浓度相关性。根据对2013—2017年每年4—9逐日花粉浓度随时间的变化趋势分析可以得知，花粉浓度峰值在4—5月和8—9月，但是每年峰值出现的时间都不相同。选择相关系数大于0.2的气象要素和花粉浓度组成特征向量，形成样本集。

3）将样本集中的2013—2016年的数据作为训练集，2017年数据作测试集。初始化参数C及γ，建立SVM回归模型，将花粉浓度预测数据和相同时刻的气象要素作为训练输入，相同时刻的花粉观测浓度作为输出。

4）使用具有自适应惯性权重的粒子群算法找出参数C及γ的最优解。

5）将优化结束之后得到的粒子群最优位置（C，γ）赋予SVM重建回归模型，得到模型预测结果。

4 实验及分析

4.1 实验环境及数据

本文使用的实验数据来源于北京7个观测站点从2013—2017年每年4—9月的花粉浓度观测资料、花粉预报、逐日气象要素等，经过预处理获得5310个可用样本，在此基础上进行本文的所有实验。预测模型是根据这些5310个数据样本的11个气象和花粉变量的数据集构建的，并利用模型对2017年花粉浓度进行了预测。

为了减少整个实验的训练时间，本文在Cloudera集群上实现了基于Spark框架的数据相关性分析和并行AWI-PSO算法。该集群由7台独立机器组成，每台机器包含32GB内存，8个Intel Xeon E-52680 V3处理器和Linux操作系统。

4.2 相关算法实现

4.2.1 数据的并行预处理

数据预处理需要完成数据的存储管理、数据的均值和方差相互关系的基本分析、数据间相关系数的计算等工作。首先，实现数据的存储。Impala是Cloudera平台下的大规模并行处理（Massive Parallel Processing， MPP）数据库引擎，使用Python编写程序，将实验数据写入Impala数据表;其次，通过调用Spark机器学习库（Machine Learning Library， MLlib）的Statistics组件实现数据均值、方差，通过分析剔除明显错误的数据，并在此基础上得出可用样本集;然后，调用MLlib的Statistics组件实现数据之间相关性系数计算，找出与花粉浓度相关的主要气象要素;最后，选择Spark on Yarn运行方式和合适的Spark运行参数组合，将这些程序提交到Cloudera集群上运行，实现并行化处理以提高数据预处理工作的时效。

AIW-PSO算法的运行效率与粒子群中粒子数目、参数的取值此处缺少了相关变量吧？请补充、参与建模的数据样本等都有关系，通常需要运行多次粒子群算法才能到达调优目的。单机模式下运行一次粒子群算法程序往往需要2～3h，因此整個参数调优的过程十分耗时。本文基于Spark框架实现AIW-PSO算法的处理。

4.2.2 花粉浓度预测模型的实现

由于MLlib的SVM组件目前只支持分类不支持回归，因此基于Python的开源机器学习库，使用最优的（C，γ）参数建立SVM的花粉浓度预测模型，对未来24h的花粉浓度进行预测。其中，SVM类型选择epsilon-SVR，核函数选择RFB核函数。

为了方便具有自适应惯性权重的粒子群算法与其他优化算法进行比较，实现了标准粒子群优化算法、传统遍历算法以及基于这些算法的SVM建模。此外，为了更进一步将SVM与其他模型相比，还实现了多元线性回归法（Multiple Linear Regression， MLR）和RBFNNBPNN请补充RBFNN的中文全称和英文全称。回复：原内容为"RBFNN"，现修改为"BPNN"的建模，然后考虑到这些优化算法本身的差异、MLlib对机器学习算法支持的局限性和编程工作量，这些算法和模型的实现选择了基于Python的开源机器学习库，程序的运行方式为单机模式运行。

4.3 实验结果的分析

4.3.1 SVM的参数优化

本文实现了AIW-PSO算法、标准粒子群算法和传统遍历方法，得到了不同算法下的最优（C，γ）参数。

1）使用AIW-PSO算法。

在参考大量文献的基础上，在本文中对PSO算法的各个参数作合理的设定。需要优化的有2个参数，因此选择粒子群的维度为2。粒子群体的大小决定了初始搜索的速度，设置为30。加速度常数取c1=c2=2，迭代步数为100，惯性权重ω取初始值为0.9。参数C的优化范围（0，10000），参数γ的优化范围为（0，20）。根据上述的模型优化过程计算，可以得到如图4所示的粒子群优化误差曲线。横轴为迭代步数，纵轴为预测结果的均方误差（MSE）。

由图4中可以看出，粒子群算法需要65步左右可以找到最优参数，收敛速度还算快。迭代100步在单机模式下需要时间为5581s，在Spark框架下则仅需要617s，得到C为592，γ为34.25，代入SVM建模得到测试样本数据预测结果的均方误差为1.85×10-2。图4为均方误差随迭代步长的变化。

2）使用传统的遍历方法。

传统的遍历方法就是设定参数C和γ的优化范围、固定优化步长，通过多次遍历循环使预测结果的均方误差在可被允许的误差范围内。为了方便比较，参数C的优化范围（0，10000），优化步长为20，参数γ的优化范围为（0，20），选取优化步长为1。从程序运行结果来看，整个优化过程在单机模式下需时间约为30965s，约8.6h，得到C为784，γ为25.37，根据所得参数重建回归模型得到测试样本的预测结果均方误差为4.18×10-2。

3）使用标准粒子群优化（PSO）算法。

标准的粒子群算法将惯性权重ω参数取一个固定值来进行计算，这是它和有自适应惯性权重的粒子群算法的唯一区别。惯性权重ω取值为0.9，其他参数与具有于有自适应惯性权重的粒子群算法取值相同。从程序运行结果来看，整个优化过程在单机模式下需时间约为19531s，得到C为478，γ为17.61，根据所得参数重建回归模型得到测试样本的预测结果均方误差为2.67×10-2。表1列出了三种优化算法的运行时间和得到的优化参数。

可以看出，几种方法建立的花粉浓度预测模型的误差水平基本相当。AIW-PSO算法建立回归预测模型所需时间最短而误差最小;与传统遍历方法相比，AIW-PSO算法建立模型的耗时减少了81.9%;与标准粒子群算法相比，AIW-PSO算法建立模型的耗时减少了71.4%，而均方误差则与它相差不远。由此可以看出，AIW-PSO算法实现简单，通过信息的共享及传递大幅度缩短了寻优时间，大幅度提高了收敛速度。

4.3.2 未来24h花粉浓度预测

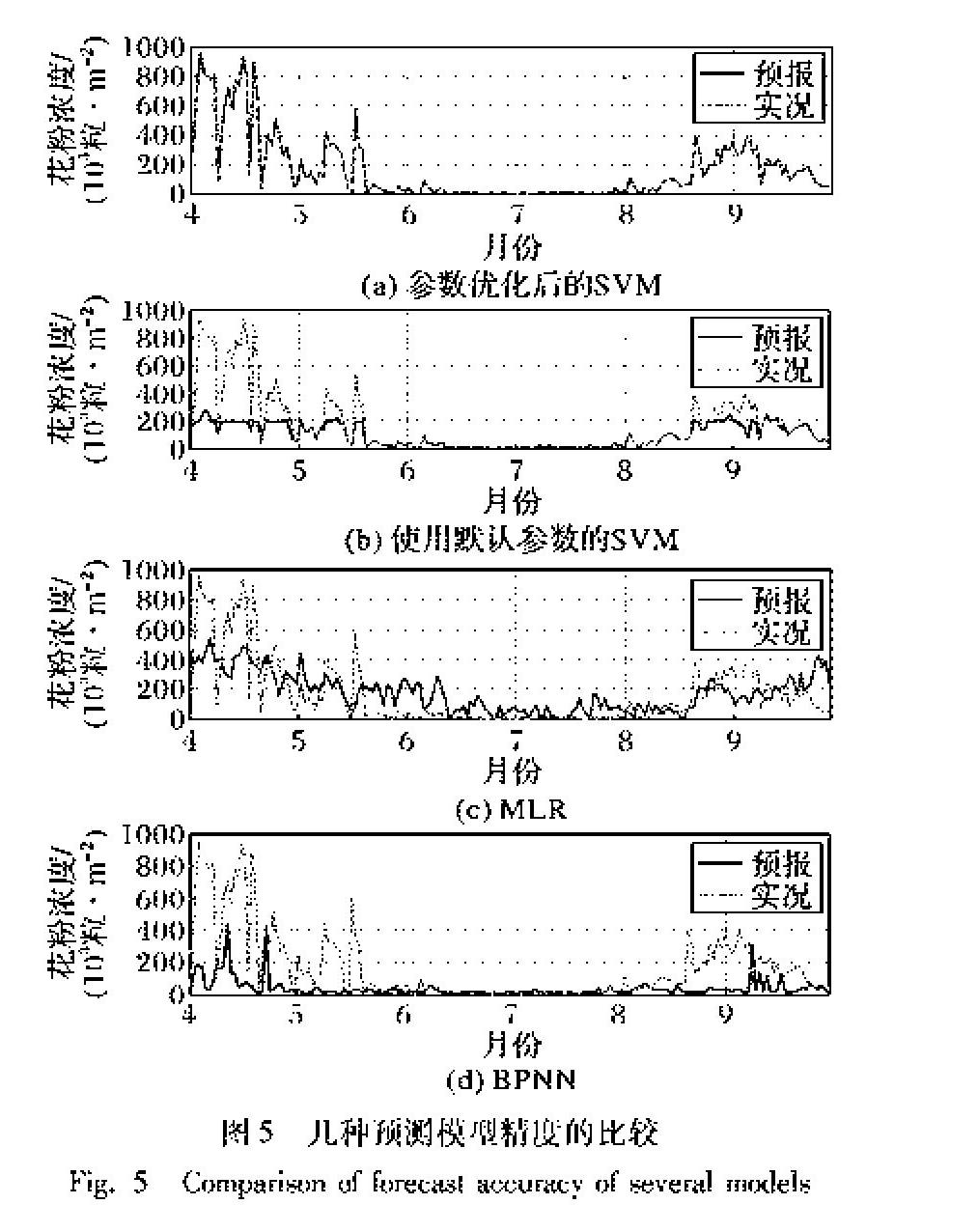
根据表1所示几种优算法的均方误差结果，选择AIW-PSO算法得到的参数结果建立优化后的SVM模型对2017年4—9月逐日花粉浓度进行预测，并将它与未优化的SVM、MLR和反向传播神经网络（Back Propagation Neural Network， BPNN）模型进行对比，四种模型下的花粉浓度预测曲线随时间的变化如图5所示。

由图5可知，对于逐日花粉浓度，各种方法的预测曲线与实际观测曲线的趋势都基本保持一致。优化后的SVM模型的预测曲线与实际观测曲线最为接近，尤其是在浓度波峰附近，表明该模型能较好地对花粉浓度峰值进行预测，这对花粉预测的社会影响有着十分积极的作用，因为花粉浓度峰值直接关系到花粉过敏症患者的病情。未优化的SVM模型的预报曲线在花粉浓度波谷部分和花粉浓度不超过200部分拟合较好，对花粉浓度峰值的预测偏离较大，预测效果不理想。MLR模型的预报曲线起伏不是很大，花粉不超过200的预测值比实际观测值偏大，而花粉浓度超过400的预测值又比实际观测值偏小很多，总之和实际观测曲线偏离较大，这个结果也从客观上验证了花粉浓度和气象要素并不是线性相关的。BPNN模型的预测曲线在花粉浓度小于100情况下拟合较好，在花粉浓度超过100的时候普遍比实际观测值偏小。相比之下，优化后的SVM模型预测效果最好。

4.3.3 平均绝对误差与MSE误差分析

本文使用均方误差和平均绝对误差（Mean Absolute Error， MAE）对预测结果进行评价。均方误差是衡量“平均误差”的一种较常见方法，可以评价数据的变化程度，均方误差的值越小，说明预测模型具有更好的精确度。图6显示了2013—2017年每年4—9月几种模型的MSE月均值分布在不同数值区间的情况。从图6可以看出，优化后的SVM模型的MSE在[0.01，56.93]区间，在（0，5]区间出现了23次，（5，50]区间出现了6次，（50，100]区间出现了1次;未优化的SVM模型的MSE在[0.01，272.33]区间，在（0，5]区间出现了3次，（5，50]区间出现了5次，（50，100]区间出现了2次，[100，200]区间出现了18次，（200，300）區间出现了2次;MLR模型的MSE分布在[23.79，343.68]区间，（5，50]区间出现了2次，在[100，200]区间出现14次，在[（200，350]区间出现了14次。优化后的SVM模型的MSE分布最多的区间为（0，50]，未优化的SVM模型的MSE分布最多的区间为（100，200]，而MLR模型的MSE大部分分布在（100，350]区间，相比之下，优化后的SVM模型MSE最小，预测精确度最高。

平均绝对误差是绝对误差的平均值，能更好地反映预测值误差的实际数量情况。图7显示了几种预测花粉浓度模型的MAE。根据图7，使用AIW-PSO算法的SVR模型达到了最佳估计成果，其五年的平均MAE仅为16.24，这是最小的并且表明绝对误差是可接受的。BPNN模型和MLR模型的MAE大于这两个SVR模型。BPNN模型的预测误差最大，而MLR模型的稳定性最差。综上所述，采用AIW-PSO算法的SVR模型预测精度最高，算法性能稳定。

4.3.4 优化后SVM模型的泛化能力

为了证明优化后的SVM模型具有泛化能力，并进一步验证改进后的模型的有效性，本文选择了北京市观象台和密云站点作为检验对象（这两个站点海拔高度差别大、基本气候条件不一样）再次进行2012年4—9月逐日花粉浓度预测，得出结果如图8所示。观察对比两个站点发现，预测曲线和实际观测曲线拟合较好，充分说明模型预测有效，具有范化能力。

5 结语

气象因素一直是影响花粉浓度预测的主要因素，分别分析单一气象因素的影响不能较好地体现出多个气象因素产生的耦合效果对它的影响规律。本文提出了一种利用SVM进行非线性回归和预测的方法，利用气象影响因子和花粉浓度观测实况数据，应用粒子群算法优化SVM参数，在此基础上建立花粉浓度预测模型。通过几个模型预测结果和误差的对比表明，优化后的SVM模型较为合理，预测精度较高，根据测试，预测结果比较接近实际观测值，同时具有较强泛化能力。

在算法的实现过程中，本文充分利用大数据技术，利用Impala技术实现样本数据的高效存储管理，基于Spark框架实现了数据预处理和部分关键算法的并行处理，大幅度提高了算法时效;然而由于Spark支持的机器学习算法有一定局限，本文涉及到的部分算法还未实现并行化的处理，这方面仍存在改进与提高的空间，所以，接下来还可以继续研究SVM回归模型算法的并行化技术，进一步提高模型的效率和精度。

参考文献 （References）

[1] 吴振玲，刘爱霞，白玉荣，等.花粉预报服务社会经济效益估算分析[J].气象，2011，37（5）：626-632.（WU Z L， LIU A X， BAI Y R， et al. Study on evaluation of economic benefits from pollen forecast and service in Tianjin [J]. Meteorological Monthly， 2011， 37（5）：626-632.）

[2] 白玉荣，刘彬贤，刘艳，等.花粉浓度预报[J].气象，2002，28（6）：56-57.（BAI Y R， LIU B X， LIU Y， et al. Pollen concentration forecast [J]. Meteorological Monthly， 2002， 28（6）： 56-58.）

[3] 刘彬贤，白玉荣.花粉浓度预报方法的初步探究[J].气象科学，2007，27（b12）：95-99.（LIU B X， BAI Y R. Primary research method on forecasting the pollen concentration [J]. Scientia Meteorologica Sinica， 2007，27（b12）：95-99.）

[4] 段丽瑶，白玉荣，吴振铃.天津地区气象要素与花粉浓度的关系[J].城市环境与城市生态，2008，21（4）：37-40.（DUAN L Y， BAI Y R， WU Z L. Relationship between pollen concentration and meteorological elements in Tianjin area [J]. Urban Environment & Urban Ecology， 2008， 21（4）：37-40.）

[5] 吴振玲，宛公展，白玉荣，等.天津气传花粉预测模型研究[J].气象科技，2007，35（6）：832-838.（WU Z L， YUAN G Z， BAI Y R， et al. Study of airborne pollen prediction model [J]. Meteorological Science and Technology， 2007， 35（6）：832-838.）

[6] 张德山，海玉龙，冯涛，等.北京地区1～4天花粉浓度预报的应用研究[J].气象，2010，36（5）：128-132.（ZHANG D S， HAI Y L， FENG T， et al. Applied research on the 1-4 day pollen concentration forecast in Beijing area [J]. Meteorological Monthly， 2010， 36（5）：128-132.）

[7] 张德山，徐景先，张姝丽，等.北京地区花粉通量演变曲线的预报模式初探[J].气象科学，2010，30（6）：822-826.（ZHANG D S， XU J X， ZHANG Z L， et al. Preliminary study on predicting model of airborne pollen flux in Beijing [J]. Meteorological Science， 2010， 30（6）：822-826.）

[8] 张姝丽，张德山，何海娟.北京城市花粉數量天气条件分析法研究[J].气象科技，2003，31（6）：406-408.（ZHANG Z L， ZHANG D S， HE H J. Study on the weather conditions of pollen concentration in Beijing city [J]. Meteorological Science and Technology， 2003， 31（6）：406-408.）

[9] 张姝丽，张德山，何海娟.北京城区8月日花粉总量和致敏花粉数量短期预报[J].气象科技，2006，34（6）：724-727.（ZHANG Z L， ZHANG D S， HE H J. Daily total pollen and allergic pollen forecasting in August in Beijing [J]. Meteorological Science and Technology， 2006， 34（6）： 724-728.）

[10] 李龙，马磊，贺建峰，等.基于特征向量的最小二乘支持向量机PM2.5浓度预测模型[J].计算机应用，2014，34（8）：2212-2216.（LI L， MA L， HE J F， et al. PM2.5 concentration prediction model of least squares support vector machine based on feature vector [J]. Journal of Computer Applications， 2014，34（8）：2212-2216.）

[11] 刘杰，杨鹏，吕文生，等.模糊时序与支持向量机建模相结合的PM2.5质量浓度预测[J].北京科技大学学报，2014，36（12）：1694-1703.（LIU J， YANG P， LYU W S， et al. Prediction model of PM2. 5 mass concentrations based on fuzzy time series and support vector machine [J]. Journal of University of Science and Technology Beijing， 2014， 36（12）：1694-1703.）

[12] 岳鵬程，张林梁，马阅军.基于模糊时序和支持向量机的高速公路SO2浓度预测算法[J].计算机系统应用，2017，26（6）：1-8.（YUE P C， ZHANG L L， MA Y J. Prediction for SO2 concentration based on the fuzzy time series and Support Vector Machine （SVM） on expressway [J]. Journal of Computer System Applications， 2017， 26（6）： 1-8.）

[13] 陈柳，吴冬梅，陈俏.小波分析及支持向量机应用于大气污染预测[J].西安科技大学学报，2010，30（6）：726-730.（CHEN L， WU D M， CHEN Q. Prediction of air pollution based on wavelet analysis and support vector machine [J]. Journal of Xian University of Science and Technology，2010， 30（6）：726-730.）

[14] 刘春波，王群芳，潘丰.基于蚁群优化算法的支持向量机参数选择及仿真[J].中南大学学报（自然科学版），2008，39（6）：1309-1314.（LIU C B， WANG Q F， PAN F. Parameters selection and stimulation of support vector machines based on ant colony optimization algorithm [J]. Journal of Central South University （Science and Technology）， 2008， 39（6）： 1309-1314.）

[15] RAKOTOMAMONJY A， LE RICHE R， GUALANDRIS D， et al. A comparison of statistical learning approaches for engine torque estimation[J]. Control Engineering Practice， 2008， 16（1）：43-45.

[16] 陈然，孙冬野，秦大同，等.发动机支持向量机建模及精度影响因素[J].中南大学学报（自然科学版），2010，41（4）：1391-1396.（CHEN R， SUN D Y， QIN D T， et al. A novel engine identification model based on support vector machine and analysis of precision-influencing factors [J]. Journal of Central South University （Science and Technology）， 2010， 41（4）：1391-1396.）

[17] YOU Z Y， CHEN W R， HE G J. Adaptive weight particle swarm optimization algorithm with constriction factor[C]// Proceedings of the 2010 International Conference of Information Science and Management Engineering. Washington， DC： IEEE Computer Society， 2010： 245-248.