新型永磁偏置三自由度磁悬浮轴承的建模与设计

赵大文，钟云龙，吴立建，方攸同

(1.上海电气风电集团有限公司,上海 200233；2.浙江大学，杭州 310027)

0 引 言

永磁偏置三自由度磁悬浮轴承采用永磁体产生偏置磁场，能对转轴提供轴向和径向三个自由度的支撑，因而可以减小系统的体积和能耗，提高转轴的临界转速，是磁悬浮轴承研究的一个重点方向[1-3]。

环形线圈是将线圈缠绕在定子轭部的线圈形式，具有端部长度短、散热效果好、槽满率高等优点。文献[4-5]在同极型径向磁悬浮轴承中使用了环形线圈以降低轴承的铜耗。但尚未有在永磁偏置三自由度磁悬浮轴承中使用环形线圈的研究。

在永磁偏置三自由度磁悬浮轴承的设计方面，因其结构复杂、相关参数多，设计难度较大。传统方法通常忽略漏磁与铁心磁阻，或用等效磁路和经验值确定铁心磁阻系数和漏磁系数，在设计时需要反复修改参数进行有限元仿真[6-9]，较为繁琐和耗时。文献[10]提出了一种参数设计和有限元循环迭代的设计方法，在参数设计时考虑漏磁系数和铁心磁阻系数，得到的结构参数采用有限元计算，循环迭代对系数进行修正，能提升设计的精度和效率。但每次循环中都要进行有限元计算，仍然较为耗时。

本文将环形线圈引入到永磁偏置三自由度磁悬浮轴承中，提出了一种新型的磁悬浮轴承。首先介绍了其结构和工作原理，接着建立了考虑漏磁、铁心非线性磁导和交叉耦合的磁路模型，并提出了一种改进的永磁偏置磁悬浮轴承的设计方法。最后，采用该设计方法设计了具体结构参数，并利用三维有限元对设计结果进行仿真验证。

1 结构与工作原理

新型永磁偏置三自由度磁悬浮轴承的结构如图1所示，由径向轴承和轴向轴承两部分通过瓦片状的永磁体和导磁块连接而成。轴向轴承部分由轴向定子、推力盘和轴向控制线圈组成。径向轴承部分采用环形线圈，相对的两个径向控制线圈串联连接。转子和推力盘做成一体，与轴向定子和导磁块一样采用实心铁磁材料制成。径向定子采用硅钢片叠压而成。永磁体轴向充磁，提供偏置磁场。

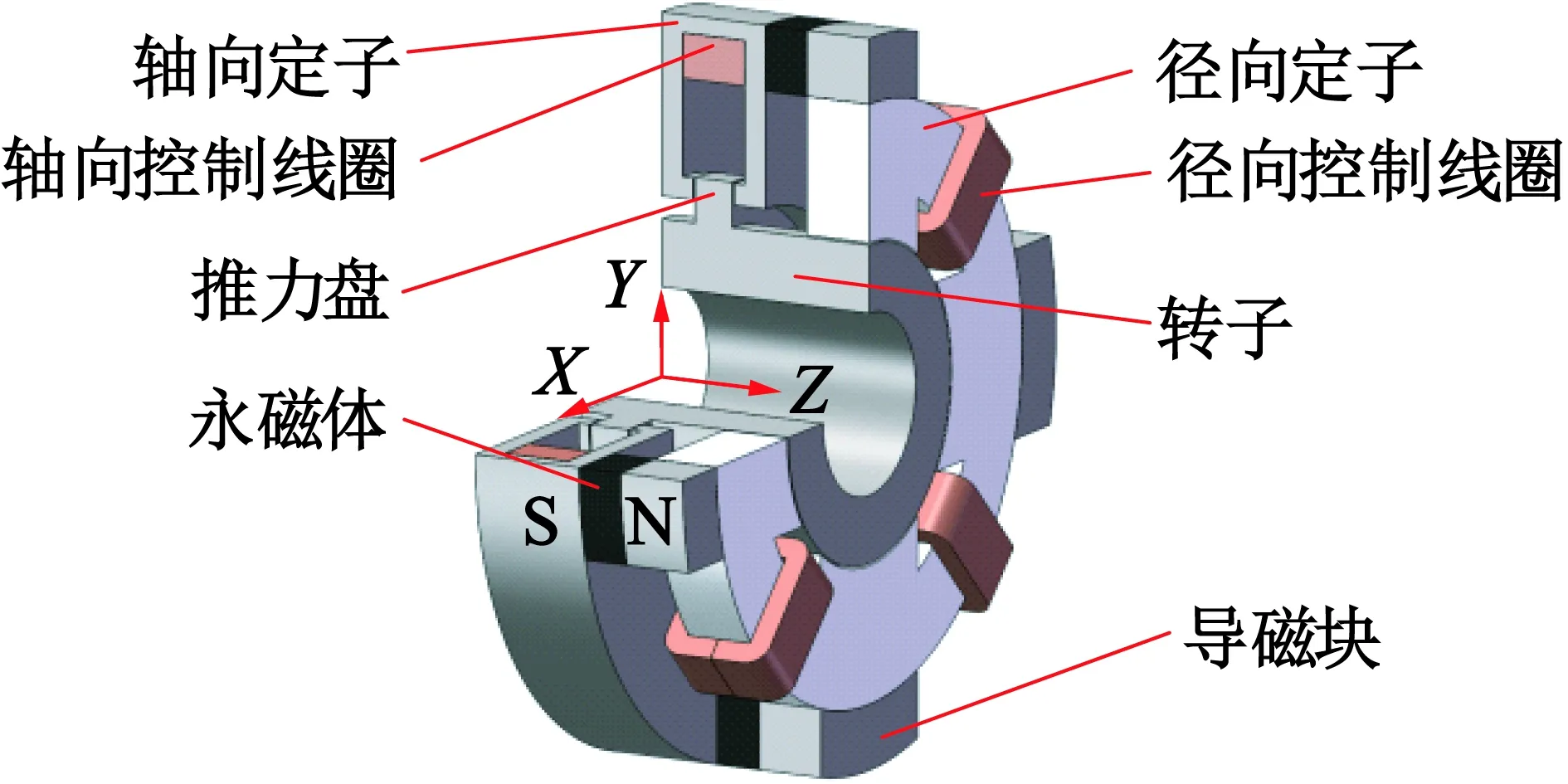
图1 新型永磁偏置三自由度磁悬浮轴承的结构

轴向控制磁通的工作原理：以图2(b)中的磁通方向为例，如果转子受到一个Z方向正向的干扰力，转子就会偏离平衡位置向Z方向正向运动，传感器检测到位移后，控制系统根据算法向轴向控制线圈中通入电流，产生轴向控制磁通，与永磁偏置磁通在轴向左边的气隙中叠加，而在右边的气隙中抵消，产生一个Z方向负向的电磁力作用在转子上，将转子拉回到平衡位置。径向控制磁通的工作原理与轴向基本一致，不同之处主要在于各线圈中的控制电流需要进行变换。根据所需要产生的电磁力的X，Y方向分量，确定对应方向的控制电流ix和iy，进而按照式(1)计算出每对环形线圈所需要通入的控制电流，线圈编号如图2(a)所示。

(1)

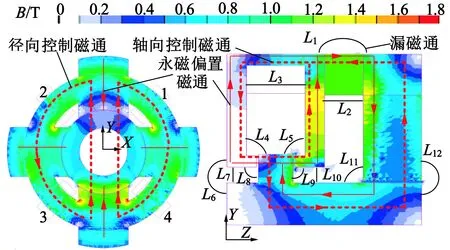
(a) 径向控制电流为2 A (b) 轴向控制电流为-2 A

图2磁场分布和磁通路径

2 磁路模型

根据图2中磁场分布和磁通路径，针对该结构的三自由度磁悬浮轴承建立磁路模型时，需要考虑以下3个问题。(1)漏磁的影响。该结构的磁悬浮轴承相对紧凑的结构会引起较大的漏磁，主要的漏磁路径如图2(b)所示。(2)交叉耦合的影响。一部分轴向控制磁通经永磁体和导磁环进入径向轴承部分，与永磁偏置磁通重合，从而影响径向轴承部分的性能。(3)铁心材料的影响。一般磁轴承的铁心材料都工作在线性区，但由于磁轴承气隙很小，导致铁心材料中的磁压降无法完全忽视，且在设计过程中，参数调整可能会引起铁心一定程度的饱和。

基于上述分析，建立如图3所示的磁路模型。该模型将永磁偏置磁场、轴向和径向控制磁场合在一起计算，因而能考虑到轴向和径向之间的交叉耦合；图2中的漏磁路径也都完全包括在内；同时计及了铁心材料的非线性磁导。

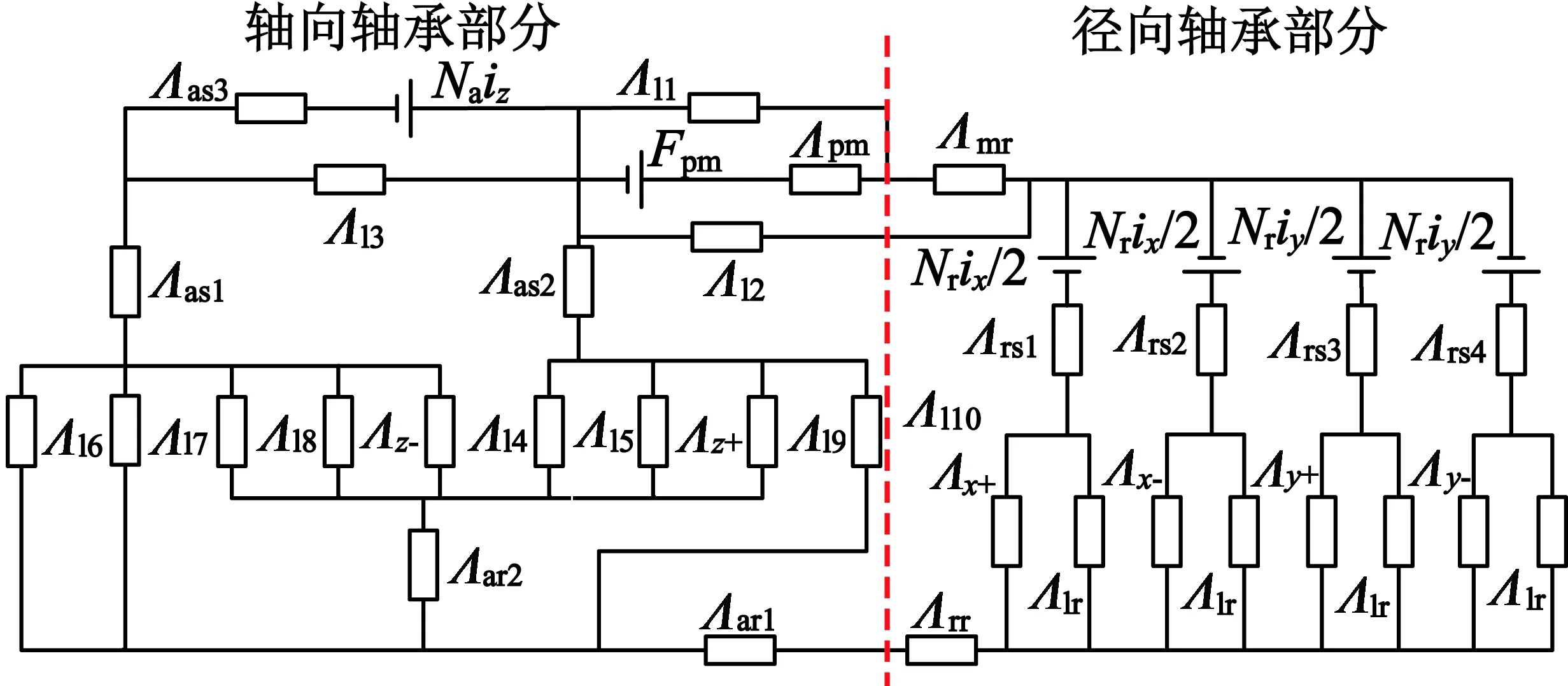
图3 磁路模型

图3中，ix，iy和iz是X，Y和Z方向的控制电流，环形线圈中的实际电流与ix，iy按式(1)进行变换。Nr，Na分别是径向控制线圈和轴向控制线圈的匝数；4块瓦片状永磁体与导磁块简化等效成一个磁动势Fpm和永磁磁导Λpm及导磁块磁导Λmr串联的支路，永磁体磁动势：

Fpm=Hclpm

(2)

式中：Hc为永磁体的矫顽力；lpm为永磁体充磁方向上的长度。定转子的铁心按磁路分成多段，Λas1～Λas3，Λrs1～Λrs4，Λar1，Λar2和Λrr分别是轴向定子、径向定子、轴向转子、径向转子对应各段的等效磁导；Λl1～Λl10是对应图2中各个漏磁路径的等效磁导；Λlr是漏磁路径L11和L12合成的等效磁导；Λz+，Λz-，Λx+，Λx-，Λy+和Λy-分别是2个轴向气隙和4个径向气隙的等效磁导(X，Y和Z轴方向各有两个气隙，按坐标系方向采用+/-号区分)。根据磁通原理，等效磁导按照近似公式计算[11]：

Λ=μrμ0Ae/le

(3)

式中：μ0是真空磁导率；μr是对应材料的相对磁导率；Ae和le是对应的等效截面积和等效长度。

磁路中的磁导按照表1中给出的相对磁导率μr、等效截面积Ae和等效长度le采用式(3)计算。表1中的x，y，z是转子在X，Y和Z方向上的位移；μdw和μdt是铁心材料DW250-35和DT4的相对磁导率；Ar是径向磁极面积，Az+和Az-是轴向磁极面积。径向磁极宽度远大于气隙，可以忽略边缘效应，但轴向磁极的宽度较小，需要对磁极面积进行修正以考虑边缘效应的影响。磁极面积的计算公式如下：

表1 磁导的计算参数

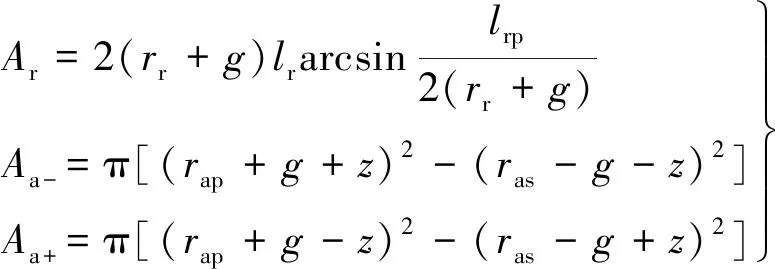
(4)

表1中的其它参数对应的尺寸标注如图4所示。

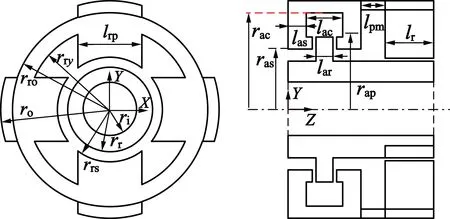
图4 尺寸参数标注

所建立的磁路模型包含了铁心材料的非线性磁导，所以需要采用牛顿法求解磁路模型得到的非线性方程组[12],得到各气隙磁通，进而计算出作用在转子上的电磁力，并在中心点位置进行线性化：

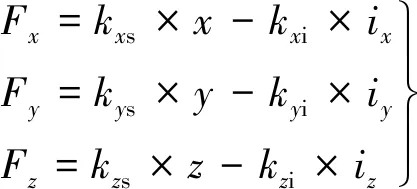
(5)

3 基于磁路模型的电磁设计

基于建立的磁路模型，对提出的磁悬浮轴承进行电磁参数设计，具体的设计流程如图5所示。在参数设计时利用漏磁系数和磁阻系数来考虑漏磁和铁心磁阻，得到结构参数后采用磁路模型计算，对系数进行校验修正，迭代至系数不变。最后采用有限元仿真进行分析验证。该方法由于采用磁路模型代替有限元法进行循环计算，可以大大提高设计效率。

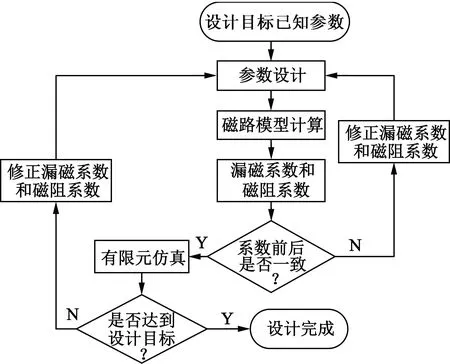
图5 设计流程

3.1 参数设计

3.1.1 气隙偏置磁密的选择

为了避免铁心材料饱和，且使轴承的承载力最大，一般选择偏置磁密和最大控制磁密相等，为铁心材料饱和磁密Bsat的一半。本文使用的铁心材料饱和磁密约为1.3 T。考虑到漏磁会使铁心中的磁密大于气隙中的磁密，且轴向气隙的漏磁较多，故选定径向气隙的偏置磁密Bbr和最大控制磁密Bcr为0.6 T，轴向气隙的偏置磁密Bba为0.5 T。值得注意的是，相同控制电流下，轴向Z+，Z-两个气隙中的控制磁密并不相同，设定Bca-为0.5 T。

3.1.2 径向轴承部分参数设计

根据设计要求的最大径向电磁力Frmax，计算得到单个径向磁极的截面积Apr，进而求得磁极面积Ar：

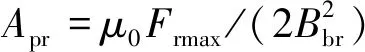
(6)

Ar=αApr/[2sin (α/2)](7)

式中:α为径向磁极弧度。单个磁极下径向气隙中的偏置磁通和最大控制磁通相等：

Φbr=Φcr=BcrAr

(8)

根据径向控制线圈的连接方式，得到的径向控制线圈最大安匝数：

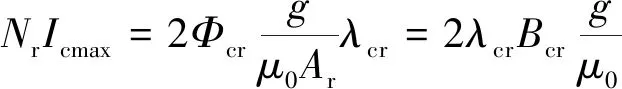
(9)

式中:λcr是径向控制磁通的铁心磁阻系数，代表铁心材料对径向控制磁路的影响。Icmax为功放电路所能输出的最大电流，确定之后可计算出径向控制线圈的匝数。同时，根据漆包线的电流密度选取导线线径d，求得径向控制线圈在槽内的截面积：

Scr=Nrd2

(10)

转子内径ri按照转轴的尺寸设定。径向控制磁通和永磁偏置磁通都会通过转子，为保证转子铁心不饱和，转子内通过的合成磁密小于饱和磁密：

(11)

进而求出满足条件的最小转子外半径rr，则径向定子内半径rrs，磁极宽度lrp和轴向长度lr分别:

rrs=rr+g

(12)

lrp=2rrssin(α/2)(13)

lr=Apr/lrp(14)

由径向定子槽内控制线圈的截面积，按照下式求得轭部的内半径:

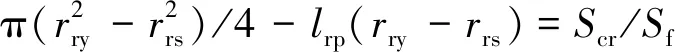
(15)

式中:Sf为槽满率，本文取0.5,以方便绕线。

径向定子轭部通过径向控制磁通，为了保持工作在不饱和区域，则:

εcrΦcr/[(rro-rry)lr]≤Bsat

(16)

式中：εcr是径向控制磁通的漏磁系数。根据上式求出满足条件的最小径向定子外半径rro。

3.1.3 永磁体及导磁块的参数设计

永磁体产生的总偏置磁通:

Φb=4εbrΦbr

(17)

式中：εbr是径向偏置磁通的漏磁系数。

永磁体工作点的磁场强度:

Hm=λb(Bbrg+Bbag)/(μ0lpm)

(18)

式中：λb为偏置磁场的铁心磁阻系数。工作点的磁通密度:

Bm=Br-BrHm/Hc

(19)

式中：Br和Hc分别为永磁体的剩磁和矫顽力。如果工作点选择磁能积最大点，永磁体的轴向长度仅为1 mm左右，难以加工。同时，永磁体有隔离轴向和径向轴承部分的作用，且轴向长度越长，永磁偏置磁通越稳定，随着转子位移变化，其改变越小，本文lpm为10 mm。单个永磁体的截面积:

Apm=Φb/(4Bm)=lrp(ro-rro)

(20)

进而求得轴承整体的外半径ro。

(4)轴向轴承部分参数设计

轴向Z+和Z-两个气隙中的偏置磁通基本相等，但是控制磁通并不相等，当通入最大控制电流时，Z-气隙中的偏置磁通和最大控制磁通相抵消，则:

式中：εba是轴向偏置磁通的漏磁系数；εca+和εca-是Z+和Z-气隙中的控制磁通漏磁系数；Bca+和Bca-为轴向Z+，Z-两个气隙中的控制磁密。考虑轴向磁极的边缘效应可求出轴向磁极的面积，则有:

π[(rap+g)2-(ras-g)2]=Aa

(22)

本文中，轴向定子与转子之间的距离取10倍的气隙宽度，以减小轴向定子与转子之间的漏磁。确定定子内半径ras后，可求出磁极外半径rap。

通过定子齿部的合成磁通应小于饱和磁通，即：

Φba/(πraplas)≤Bsat

(23)

根据式(23)求出定子齿部轴向长度las。

轴向控制线圈最大安匝数:

NaIcmax=(Φca-+Φca+)gλca/(μ0Aa)=

λca(1+εca-/εca+)Bbag/μ0

(24)

式中:λca是轴向控制磁通的铁心磁阻系数。根据功放电路能输出的最大电流Icmax确定线圈匝数Na和导线线径d，求得轴向控制线圈在槽内的截面积:

Sca=Nad2

(25)

推力盘中通有偏置磁通，为防止出现饱和，有:

Φba/(πrrlar)≤Bsat

(26)

推力盘需要承受轴向的电磁力，因而其轴向长度不能太小。根据上式计算值和受力情况，综合分析得到推力盘的轴向长度lar。

轴向定子轭部有轴向控制磁通和偏置磁通，则:

(27)

轴向定子外径与轴承整体外径相同，则可根据式(27)计算出定子槽外半径为rac。

根据定子槽内线圈的截面积，按下式计算得到定子线圈槽的轴向长度lac：

lac(rac-rap)=Sca/Sf

(28)

推力盘与轴向控制线圈需要一定距离,保证线圈的安装，同时防止两者相接触，所以槽满率Sf取0.3。

3.2 设计要求、已知参数及设计结果

气隙宽度g越小，所需励磁磁动势也越小，能减小控制线圈的尺寸和铜耗以及永磁体的用量，缩小轴承整体体积。但是，过小的气隙难以加工实现，也会提高控制的难度。综合考虑，本文的气隙宽度g设置为0.5 mm。永磁体材料选择钕铁硼，型号为N38H，剩磁Br为1.24 T，矫顽力Hc为887.5 kA/m。转轴的外半径为20 mm，径向磁极弧度α为0.4π，最大控制电流Icmax为2 A。设计要求径向最大电磁力为350 N，而轴向最大电磁力大于400 N。

漏磁系数和铁心磁阻系数的初始值设为1，经过图5的设计流程，迭代收敛后得到漏磁系数和铁心磁阻系数如表2所示，设计结果如表3所示。

表2 漏磁系数和铁心磁阻系数

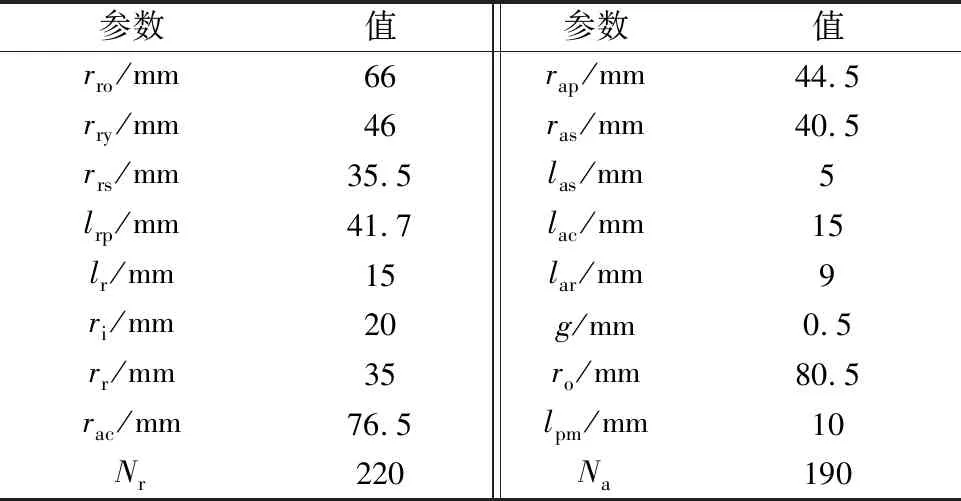
表3 设计结果

4 三维有限元仿真分析

为了验证电磁设计的合理性和磁路模型的准确性，根据设计结果建立三维有限元模型，进行仿真分析。计算得到的永磁偏置磁场分布如图6所示。铁心中大部分区域的磁密小于0.8 T，而靠近永磁体的局部磁密较高，达到了1.3 T左右。总体而言，铁心基本未出现饱和，有利于电磁力特性的线性化。径向和轴向气隙中的偏置磁密分别为0.62 T和0.52 T，稍高于设计值，但误差在可接受的范围内，符合设计要求。因为漏磁的存在导致磁极铁心中的磁密稍大于气隙磁密，特别是轴向轴承部分的漏磁较为明显，这验证了本文气隙偏置磁密选择的合理性。

(a) 径向截面

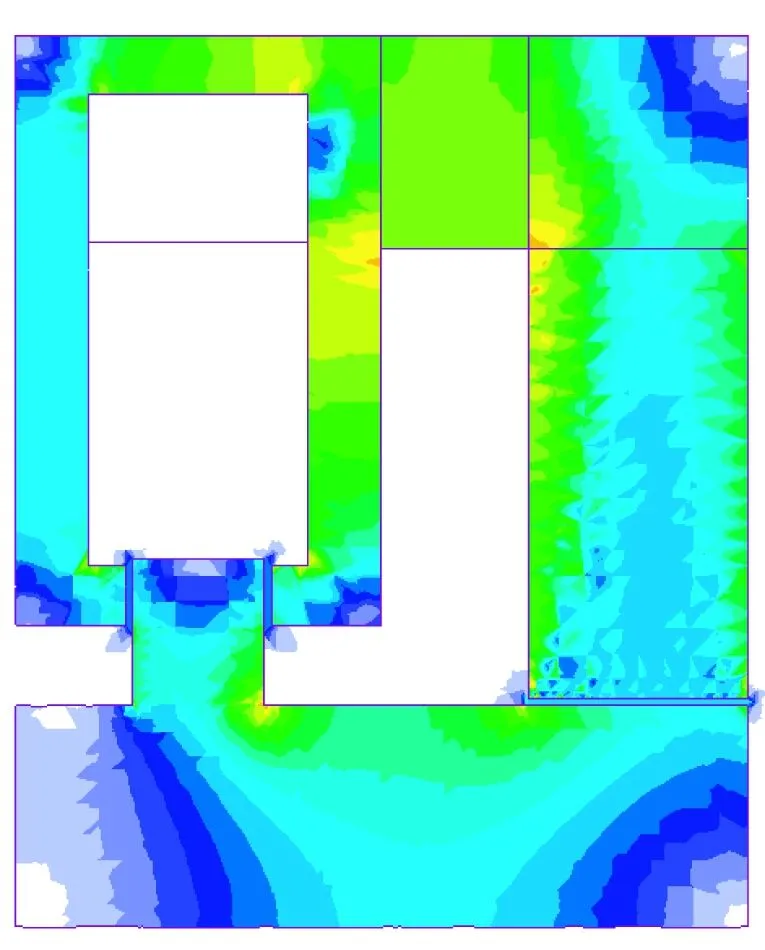
(b) 轴向截面

当Y方向控制电流2 A时，径向轴承部分的磁场分布如图2(a)所示。铁心材料中的磁通密度基本保持在1.3 T以下，未出现饱和现象。对应方向的一侧气隙磁通密度减小到0.08 T，另一侧气隙的磁通密度增加到1.15 T。当轴向控制电流为-2 A时，轴向的磁场分布如图2(b)所示。铁心材料同样未出现饱和，一侧气隙磁密增加到0.91 T，另一侧气隙磁密减小到0.01 T。

图7为径向电磁力特性。径向电磁力与径向控制电流的关系基本为线性，有利于简化控制器的设计，满足了设计的要求。而径向电磁力与位移的关系整体呈非线性，这是磁悬浮轴承结构所具有的固有特性。但转子在中心点位置附近时，电磁力与位移的关系接近线性。考虑到在实际应用中，转子位移远小于气隙宽度，所以可对径向电磁力-位移特性进行线性化以简化控制模型。图8为轴向电磁力特性。轴向电磁力与轴向控制电流的关系呈现非线性，轴向控制电流为-2 A时，轴向电磁力为444.4 N，而轴向控制电流为2 A时，轴向电磁力为-558.5 N。这是由于轴向和径向轴承部分并排的结构导致轴向两个气隙中的控制磁通不相等所引起的。轴向电磁力与位移的关系和径向情况相同。同样可对轴向电磁力特性在中心点附近进行线性化。

从结果可以看出，磁路模型的结果和有限元仿真结果基本吻合，验证了所建立的磁路模型的准确性和设计结果的合理性。

(b) 电磁力-位移

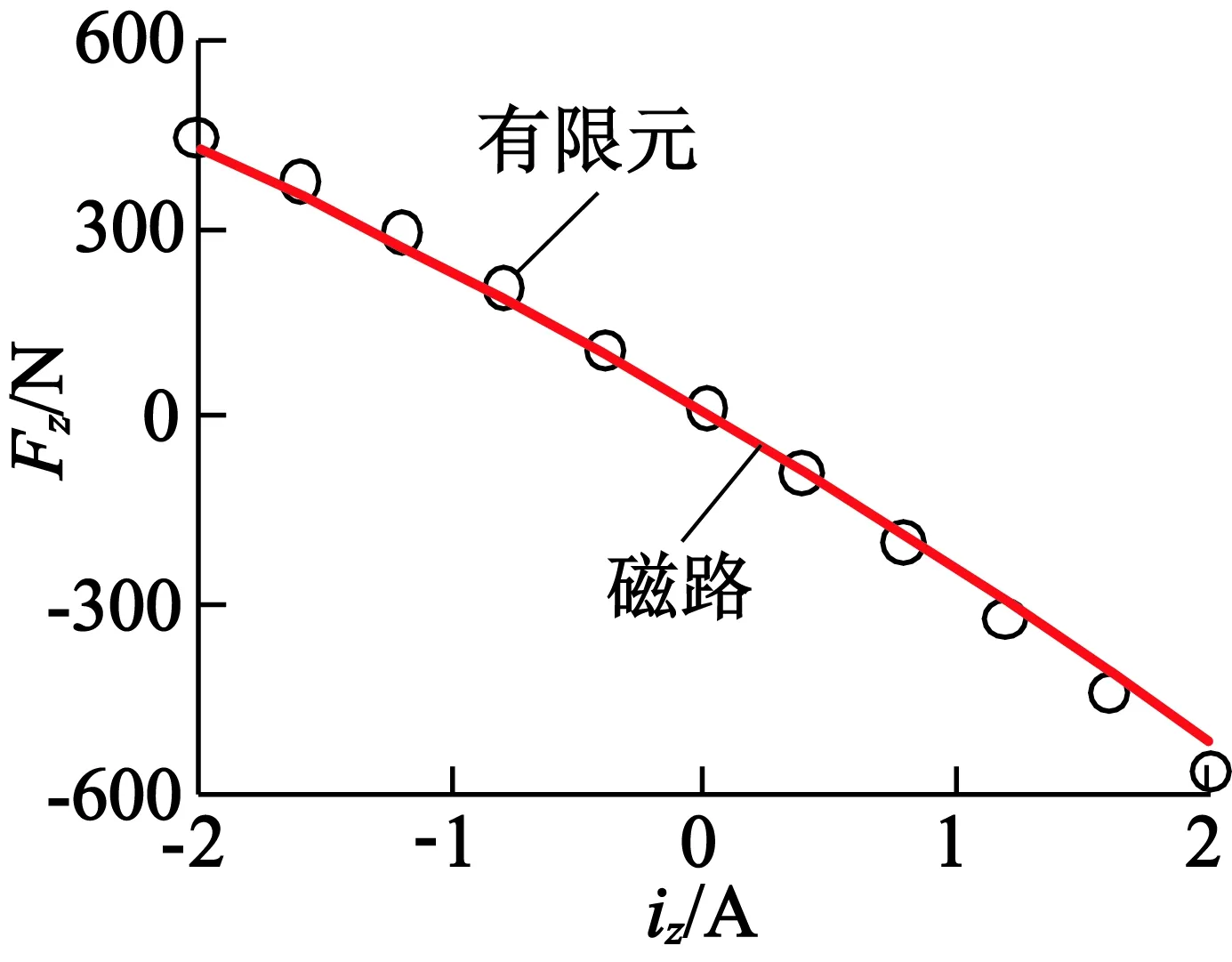
(a) 电磁力-控制电流

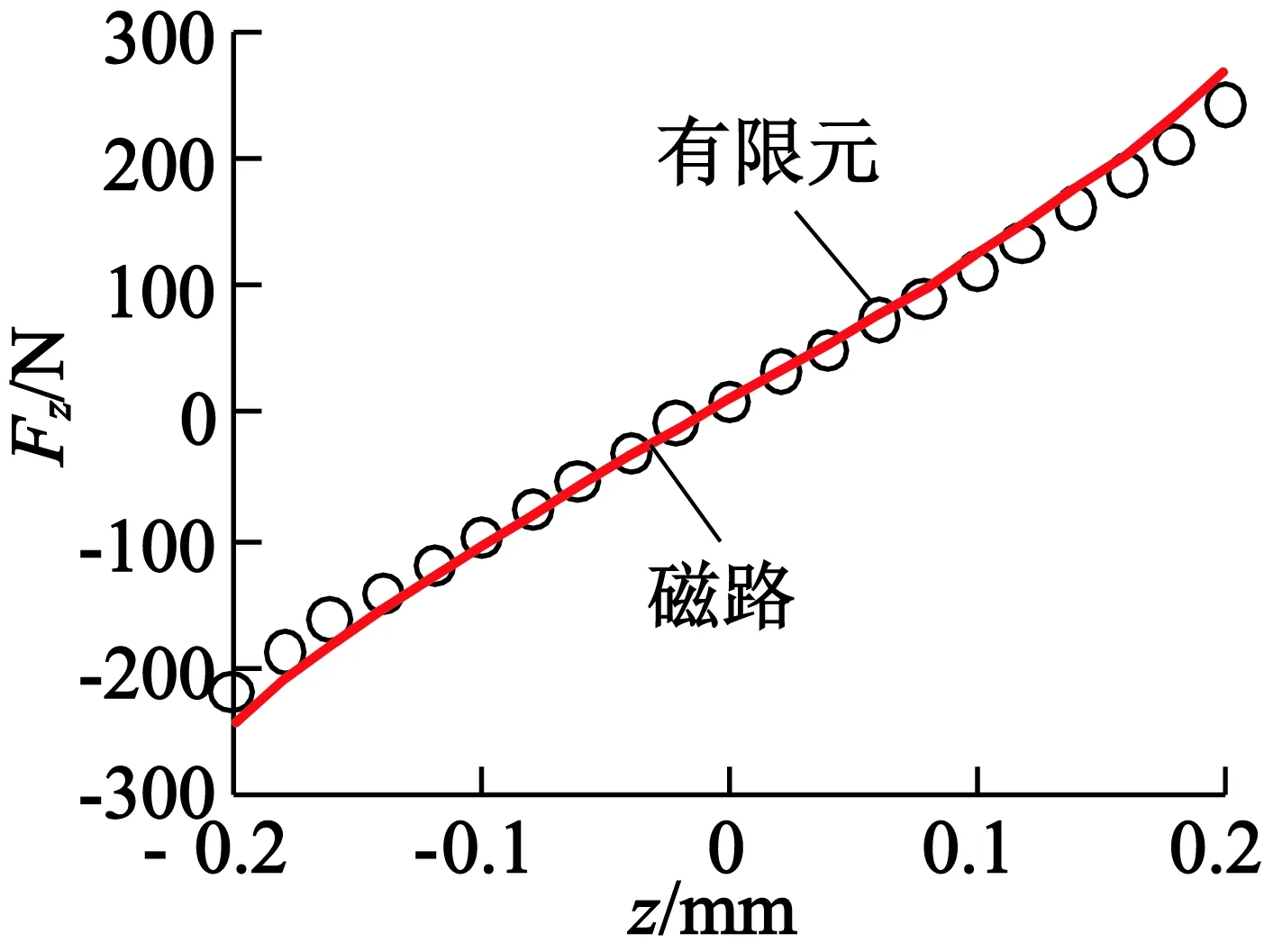
(b) 电磁力-位移

5 结 语

本文研究了一种新结构的永磁偏置三自由度磁悬浮轴承，径向控制线圈采用环形线圈，由永磁体提供偏置磁场，整体铜耗较低。建立了计及漏磁、铁心非线性磁阻和交叉耦合的磁路模型，基于该模型提出了一种改进的永磁偏置磁悬浮轴承的设计方法，能有效地提高设计效率。磁路模型的准确性和设计结果的合理性得到了三维有限元的仿真验证。建模和设计的思想同样适用于其他类型的磁悬浮轴承。