基于最大联合条件互信息的特征选择

毛莺池 曹海 平萍 李晓芳

摘 要：在高维数据如图像数据、基因数据、文本数据等的分析过程中，当样本存在冗余特征时会大大增加问题分析复杂难度，因此在数据分析前从中剔除冗余特征尤为重要。基于互信息（MI）的特征选择方法能够有效地降低数据维数，提高分析结果精度，但是，现有方法在特征选择过程中评判特征是否冗余的标准单一，无法合理排除冗余特征，最终影响分析结果。为此，提出一种基于最大联合条件互信息的特征选择方法（MCJMI）。MCJMI选择特征时考虑整体联合互信息与条件互信息两个因素，两个因素融合增强特征选择约束。在平均预测精度方面，MCJMI与信息增益（IG）、最小冗余度最大相关性（mRMR）特征选择相比提升了6个百分点;与联合互信息（JMI）、最大化联合互信息（JMIM）相比提升了2个百分点;与LW向前搜索方法（SFS-LW）相比提升了1个百分点。在稳定性方面，MCJMI稳定性达到了0.92，优于JMI、JMIM、SFS-LW方法。实验结果表明MCJMI能够有效地提高特征选择的准确率与稳定性。

关键词：信息熵;互信息;条件互信息;联合互信息;特征选择

中图分类号： TP393.0

文献标志码：A

文章编号：1001-9081（2019）03-0734-08

Abstract： In the analysis process of high-dimensional data such as image data， genetic data and text data， when samples have redundant features， the complexity of the problem is greatly increased， so it is important to reduce redundant features before data analysis. The feature selection based on Mutual Information （MI） can reduce the data dimension and improve the accuracy of the analysis results， but the existing feature selection methods cannot reasonably eliminate the redundant features because of the single standard. To solve the problem， a feature selection method based on Maximum Conditional and Joint Mutual Information （MCJMI） was proposed. Joint mutual information and conditional mutual information were both considered when selecting features with MCJMI， improving the feature selection constraint. Exerimental results show that the detection accuracy is improved by 6% compared with Information Gain （IG） and minimum Redundancy Maximum Relevance （mRMR） feature selection; 2% compared with Joint Mutual Information （JMI） and Joint Mutual Information Maximisation （JMIM）; and 1% compared with LW index with Sequence Forward Search algorithm （SFS-LW）. And the stability of MCJMI reaches 0.92， which is better than JMI， JMIM and SFS-LW. In summary the proposed method can effectively improve the accuracy and stability of feature selection.

Key words： information entropy; Mutual Information （MI）; conditional mutual information; joint mutual information; feature selection

0 引言

隨着数据时代不断发展，大数据应用越来越彰显出它的优势，如图像数据分析、基因数据分析、文本数据分析等。高维数据能够详细记录事物的属性，同时也存在着大量冗余数据，冗余数据给数据分析带来了巨大难题。特征选择方法能从高维数据中分析抽取出相关特征，减小数据维数，降低分析复杂度。基于互信息的特征选择是Filter[1]类型特征选择方法一个重要研究方向。互信息在相关性分析上有计算简单、可解释性强特点，因此基于互信息的特征选择方法被广泛应用于特征选择。如Fleuret等[2]提出通过考虑条件互信息降低数据维数的条件互信息特征选择方法。特征选择效率及策略方面也有相关研究，一种贪婪向前搜索的联合互信息特征选择方法被提出，用于解决互信息计算过程中效率问题[3]。现有互信息特征选择方法主要从3个方面展开研究：信息增益、条件互信息和联合互信息。其中条件互信息及联合互信息在随着特征不断选择过程中计算变得复杂。针对条件互信息及联合互信息计算复杂问题，一种启发式方法被应用在特征选择当中，启发式计算方式大幅降低了互信息计算难度[4]。

基于启发式计算互信息评判特征重要性时，不同的特征选择方法评判标准有所不同。如信息增益方法单独考虑每个子特征同目标分类之间相关性，未考虑特征与特征之间关系。联合互信息考虑整体互信息大小，未考虑单个特征同目标之间的相关性。基于最大联合互信息考虑互信息的整体稳定性，未考虑联合互信息整体大小。针对现有联合互信息计算方法存在的不足，本文提出基于最大联合条件互信息的特征选择方法（feature selection method based on Maximum Conditional and Joint Mutual Information， MCJMI）。MCJMI特性選择方法基于联合互信息整体稳定性的基础上，利用条件互信息，挑选出使整体互信息增长最显著的特征。MCJMI特征选择方法既保证了联合互信息在整体上的稳定性，同时使所选特征与分类之间的整体互信息增量最大。

1 相关工作

随着特征选择领域研究不断发展，产生了各种类型的特征选择方法。基于互信息理论的特征选择方法最终目的是从所有特征中挑选出指定个数最相关的特征降低高维分类问题复杂度[5]。

基于信息增益（Information Gain， IG）的特征选择最早应用于特征选择，通过IG分析特征与分类之间相关性大小从而排除冗余特征[6]。IG在特征选择过程中计算简单，仅考虑每个特征与分类之间的互信息大小，能在o（n）时间复杂度内完成。由于IG选择条件简单，为了增强冗余特征判断， Liu等[7]提出了一种基于类别与类别之间特征分布改进的IG文本方法。

Battiti等[8]提出基于互信息的特征选择方法（Mutual Information Feature Selection， MIFS），MIFS方法既考虑已选特征与分类之间的互信息，同时考虑已选特征与未选特征之间的相关性，MIFS不再假设特征之间独立。其计算方式分析主要由两部分组成，一部分为未选特征与分类之间的互信息，另一部分为未选择特征与已选特征互信息求和。MIFS存在多个改进版本，如Hoque等[9]研究的MIFS-ND方法，Cho等[10]提出的归一化互信息特征选择（Normalized Mutual Information Feature Selection， NMIFS）方法其在表现上都优于MIFS。

Peng等[11]将最大依赖性、最大相关性和最小冗余度准则应用到特征选择当中，提出了基于互信息的特征选择最大依赖性、最小冗余度和最大相关性（minimum Redundancy Maximum Relevance feature selection， mRMR）准则的特征选择方法。mRMR特征选择将MIFS方法中参数处理成已选特征个数的倒数使选择标准一致。

基于联合互信息的特征选择方法在子特征选择中也有广泛应用。董泽民等[12]使用基于联合互信息（Joint Mutual Information， JMI）的特征选择方法。JMI加入了分类变量，在特征选择时不仅需考虑所选特征同分类之间的关系，同时，考虑在有分类条件下子集特征与未选特征之间的互信息大小。Bennasar等[13]提出了一种基于最大化联合互信息（Joint Mutual Information Maximisation， JMIM）的特征选择方法，JMIM考虑联合互信息整体稳定性。

基于条件互信息的特征选择同样也有着广泛的应用。Li等[14]提出了一种通过条件互信息改进的自适应稀疏群套索方法，改进了分块下降方法，提高了分类选择的精度。在互信息发展的过程中，也出现了类型相同的特征选择方法，如Liu等[15]提出的LW索引向前搜索方法（LW index with Sequence Forward Search algorithm， SFS-LW）。SFS-LW特征选择方法与上述JMIM方法在计算选择过程相似，不同的是SFS-LW采用了基于类与类之间距离作为特征选择的标准。

综上，特征选择方法根据特征与分类之间的互信息大小，作为特征选择评判标准。在评判特征是否冗余时，考虑的标准单一，如仅考虑联合互信息或仅考虑条件信息就造成了不同特征方法选择结果不同。本文采用联合互信息与条件互信息结合的方式，分析特征之间的冗余性，以提高对冗余特征的筛选效果。

4 MCJMI特征选择方法

4.1 总体思路

MCJMI方法从联合互信息与条件互信息两部分考虑所选择特征，同时结合最小最大原则作特征选择选择过程中涉及两个部分：特征与分类之间的相关性分析，已选特征与未选特征之间的冗余分析。提出的方法，主要解决现有联合互信息方法在特征选择过程中出现的无法排除冗余及不相关特征选择问题。最终方法在指定子集大小情况下，挑选出子集S使I（S;C）最大。

4.2 最大最小互信息

最小最大联合互信息相似集合：通过最小联合互信息计算得到加入不同未选特征的最小联合互信息集合。在最小联合互信息集合中找出最大值。若集合中存在与最大值相等或相似值时加入到最小最大联合互信息相似集合，该集合公式表示如下：

4.3 最大联合条件互信息

特征选择过程中，希望每次选择的特征能够最大限度地提升S与分类C之间的互信息值。根据特征选择的特点，提出了MCJMI方法。最大联合条件互信息不仅考虑每次联合互信息是否最大，同时考虑条件互信息是否满足要求。条件互信息排除与子集S冗余的特征，增强了特征选择的约束。

4.4 方法步骤

根据4.3节特征之间相关性冗余性分析，本文提出基于最小最大联合条件互信息的特征选择方法，计算公式如式（20）、（21）所示：

当fi满足式（21）集合时，由最小最大联合互信息知，当加入fi满足了在所有特征子集中，至少存在一个特征使得联合互信息大于其他特征。当存在多个相似值时，方法判断其对子集特征的整体增量，通过整体互信息增量排除冗余性特征。通过增量大小方法确定最终要选择的特征，其方法流程如下：

MCJMI方法流程。

MCJMI方法流程中，F为数据样本所有特征，n表示特征量，C表示样本对应的分类。num、m分别表示最终要选择的特征数量与最大相似集合的大小。P表示特征输入时的下标，方法流程中的List用来存储每次计算的联合互信息。方法循环计算，每次挑选出最适合的特征子集，当子集大小满足|S|=num方法结束。MCJMI在每次计算特征互信息时间复杂性为o（|C|）。根據方法流程得出方法复杂度与需要选择的特征数num，待选特征集合大小|F-S|相关，同JMIM方法复杂度相同。

5 实验验证

5.1 实验方案

实验数据来自UCI公开数据集[17]，如表4所示，其中数据集Breast-cancer、Sonar、Parkinsons在文献[10]使用到，使用相同数据集以达到验证实验结果的作用。剩余数据集则根据不同数据类型从UCI数据集挑选所得。实验中按照数据集的样本大小，将数据分为两个部分具体见表4。表4中编号1～4数据集属于较少样本的数据集，编号5～7数据集属于样本较多的数据集，编号8数据为非平衡数据集。

每个数据集随机划分80%数据作训练集，20%数据作测试集。实验数据中存在离散型数据、连续型数据、离散+连续型数据，为保证特征选择模型能够适用计算连续及离散特征数据类型，采用基于K-近邻（K Nearest Neighbors， KNN）互信息计算方法[18]。所有数据集数据采用归一化方法处理到0～1区间以降低特征选择过程计算复杂度。

实验中将MCJMI与IG、mRMR、JMI、JMIM、SFS-LW五种特征选择方法作比较，其中SFS-LW作用对比与现有方法效果。为验证特征选择的效果，方法将已选的特征子集S输入到KNN（n=3）及贝叶斯分类模型中作分类正确率预测得到分类精度。，通过分类的正确率评判选择特征的合理性。为避免出现偶然性的实验结果，实验中分别对每个数据集进行5次实验，预测结果取均值，具体实验流程如图1所示。

5.2 小样本数据预测精度分析

图2中横坐标表示数据集上选择的特征数量，纵坐标表示对应特征数量下，KNN与贝叶斯分类平均预测精度。图2给出了样本较少数据集上各个方法在特征选择过程中预测精度变化情况。

通过Flowmeters、wine、Sonar、Parkinsons数据集上不同特征方法下分类预测精度变化图可得出以下结论：

1）如图2所示MCJMI在样本较少数据集上预测结果。Flowmeters数据集上MCJMI、JMIM、JMI、mRMR、SFS-LW仅在特征选择数5左右预测精度已经达到最高值，分别为83%、80%、80%、75%、80%。IG在特征数达20左右才到达最大精度75%。虽然JMIM、JMI、mRMR方法在特征数5左右也都达到了最大精度，从预测精度上能够得出MCJMI比其他方法相比精度都要高。MCJMI达到最大预测精度后，随着选择特征加入预测精度始终稳定，而mRMR、IG则有较大的波动。在parkinson数据集上MCJMI也仅在特征选择数到10左右预测精度已经达到了92%，并且其产生的波动也较小。其主要原因在于特征选择过程MCJMI通过条件互信息排除了冗余特征。在Sonar数据集上看出，几种算法在特征数都无较好的稳定性，当特征数达到30后，MCJMI预测精度达到了88%且趋于平稳。

2）从特征不断增加过程中预测精度变化趋势看，特征数逐渐增加时，所有特征选择方法在数据集上预测精度呈现先增加后减小的规律。这符合了随着新特征的加入，信息量在不断增加，冗余信息也在不断增加的规律。图2中MCJMI、JMI、JMIM选择的特征加入后预测精度不断增加，达到一定特征数量后预测精度呈现下降趋势一致。从图2可以看出，MCJMI很好地反映这一规律，而IG、mRMR这一特征表现并不明显，而且出现预测精度上下跳跃的情况。主要原因在于IG，mRMR在特征选择时考虑的标准单一，选择的冗余特征加入后为分类提供的信息量较少，造成预测精度上升较慢。

3）MCJMI与SFS-LW方法在预测精度上差异较小，但根据MCJMI与SFS-LW在精度曲线变化上，可以看出 MCJMI在精度变化过程中平稳性优于SFS-LW。主要原因，MCJMI在每次计算过程中基于前一特征计算互信息和。而SFS-LW每当加入特征后，将会重新计算度量各个分类之间距离，降低了已选特征之间的关联性。

从表5中不同数据集上平均精度上看，在wine数据集上平均精度MCJMI相对IG提升了56.1个百分点，相对mRMR、JMI、JMIM、SFS-LW平均预测精度无明显大小变化;在Parkinsons数据集上MCJMI相对IG提升了43.8个百分点，相对mRMR提升了33.5个百分点，相对JMI、JMIM、SFS-LW平均预测精度无明显大小变化;在Flowmeters数据集上MCJMI相对IG提升了55.1个百分点，相对mRMR提升了54.8个百分点，相对JMI、JMIM平均预测精度提升了1.8和2个百分点，相对SFS-LW提升了11.7个百分点;在Sonar数据集上MCJMI相对IG提升了77.8个百分点，相对mRMR提升了45.4个百分点，相对JMI、JMIM平均预测精度提升了1.5和2.5个百分点。

根据表6中达到最大精度所选特征数占比得出，IG所占总特征比例变化范围为13.64%～83.33%，其波动区间大小为70%。同理得mRMR波动区间大小45%，JMI波动区间大小42%，JMIM波动区间大小15%，MCJMI波动区间大小38%，SFS-LW波动区间大小为38%与MCJMI相同。IG波动较大主要原因IG未考虑特征之间的相关性，特征相关性较强时为达到高的预测精度，IG特征选择数量要多于其他方法。JMI，JMIM，MCJMI波动区间相似，而每个数据集上达到最大精度时所选特征占比上得出，MCJMI与SFS-LW选择特征数低于JMI与JMIM。

5.3 大样本数据预测精度分析

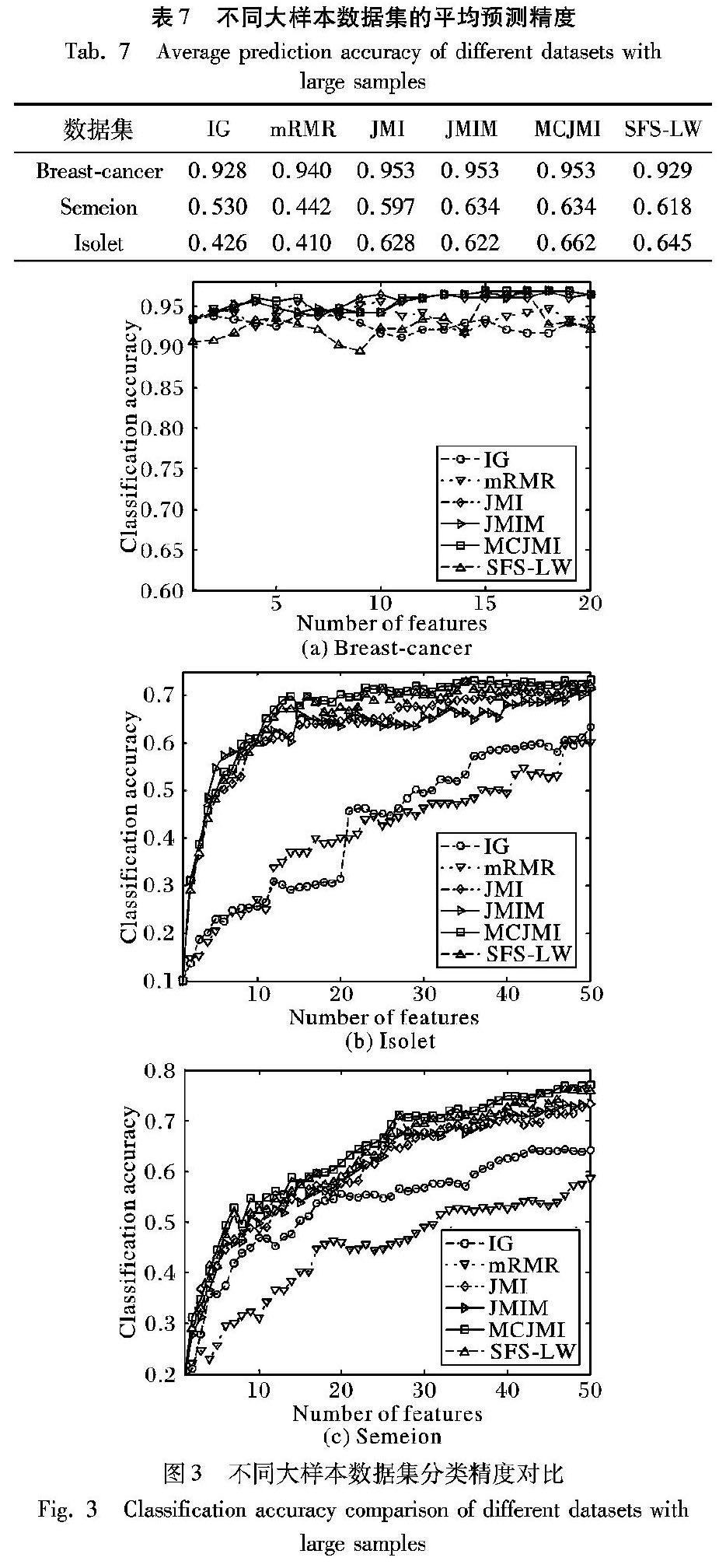
图3给出样本数量较多的数据集上分类预测精度。其中：break-cancer选择特征选择过程前20个特征，Isolet及semeion选取特征选取过程前50个最相关特征作分类预测。详细预测精度见图3。

根据图3比较可得出以下结论：

1）数据样本量较多时，几种特征选择方法在随着特征选择的过程中预测精度不断增加几种特征选择方法在随着特征数量增加时分类精度也在不断增加，而SFS-LW则出现了预测进度上下浮动较大的情况。Breast-cancer数据集上当特征量在4时MCJMI、JMIM、JMI预测精度达到96%，SFS-LW预测精度达到94%。在之后出现了精度下降，主要原因在于SFS-LW每选择一次特征后都需重新计算分类间距离，当样本数据存在较多噪声时，即数据非平稳数据就存在如图3（a）所示情况。IG、mRMR在特征4时预测精度为93%出现明显下降。主要原因是IG、mRMR选择了冗余特征，增加了数据噪声。在Isolet数据集上特性选择数量8左右出现JMIM预测精度短暂优于MCJMI情况，在特征数量达到10以后MCJMI预测精度优于其他几种方法。

2）图3（a）、（c）数据集上特征选择预测精度曲线变化的斜率得出，MCJMI预测精度上升的速度要优于IG、mRMR、JMI、JMIM。SFS-LW方法同样预测精度优于IG、mRMR、JMI、JMIM。其主要原因MCMI方法在特征选择时考虑了条件互信息加入特征fj后，总能使I（fi，S;C）向增长速度最快的方向选择特征，SFS-LW每次加入特征最大限度的区分类，忽略了特征选择稳定性。

根据表7对不同数据集上预测的平均精度对比得出，在Breast-cancers数据集上，JMI、JMIM、MCJMI最大预测精度相差不大，MCJMI相对IG提升了32.5个百分点，相对mRMR精度提升了31.3个百分点，相对SFS-LW提升了32.4个百分点;在Semeion数据集上，MCJMI相对IG提升了1014个百分点，相对mRMR提升了1919.2个百分点，相对JMI提升了33.7个百分点，相对于SFS-LW提升了11.6个百分点;在Isolet数据集，MCJMI相对IG提升了2423.6个百分点，相对mRMR提升了2423.6个百分点，相对JMI提升了43.4个百分点，相对JMIM提升了4个百分点。从平均预测精度上得出，MCJMI特征选择预测精度整体上高于其他方法。

5.4 非平稳数据预测精度分析

图4给出非平衡数据集secom不同特征选择方法的预测精度，选取前100个特征预测结果。图5给出不同特征选择方法在特征选择过程时间复杂度情况。

根据图4预测计算精度方面能够得出：在特征数到达30之前，基于互信息的特征选择方法在精度预测方面优于SFS-LW;特征达到30之后，SFS-LW在预测精度明显高于互信息的特征选择方法。主要有以下原因：

1）基于互信息特征选择计算过程中，互信息计算基于各类样本所占比例。在特征选择前期不均衡样本，某一类样本占比例较大，互信息所选择的特征倾向于占比重大的分类样本。

2）SFS-LW计算类与类之间距离，各个类之间计算距离，对样本的比例大小敏感度不高，但当选择特征较少时，数据噪声对SFS-LW影响较大，正如图4所示SFS-LW在特征到达30之前精度低于MCJIM方法。

根据图5可以得出：在特征选择过程中SFS-LW时间复杂度最高，SFS-LW在每次计算类与类之间距离时为组合问题;而MCJMI在特征选择过程中，计算互信息与|C|的大小有关且在计算相似集合时消耗了较多时间;JMI、JMIM计算时间复杂度相同;mRMR时间复杂度略低于JMI与JMIM，IG时间复杂度最低。

5.5 稳定性分析

稳定性是评判方法泛化能力的重要指标，特征选择结果易受样本选择的影响。对于同一数据集中不同数据样本，若所选出的最优特征子集越相似说明方法越稳定。Chelvan等[19]提出相似特征稳定性的评判标准。设S1，S2为同一数据集上不同样本上所选出的两个最优子集，其中两者子集中的特征个数为|S1|=|S2|记作m，|F|为总特征数n，S1，S2相交的个数r=|S1∩S2|，则稳定性计算公式如下：

由式（22）得出当所选特征数一定时，r=|S1∩S2|交集越大则说明方法在选择特征上越稳定。表8中给出各个方法平均精度、稳定性，由于稳定性仅能够说明算法在特征选择上的稳定。通过平均精度与稳定性的比值，能够标准化稳定性分析结果。本文给出平均精度与稳定性的比值，作为算法最终稳定性评判指标，具体如表8所示。

从表8中可以看出，IG的稳定性最高，值为0.9025，mRMR稳定性为0.8803，MCJMI稳定性为0.8760，SFS-LW稳定性为0.8800。主要原因是IG所考虑的条件最少，仅存在特征与分类之间的互信息大小。JMI、JMIM稳定性处于几个方法中较低的水平，主要原因是JMI、JMIM在计算选择过程中考虑的因素要多于IG与mRMR，受样本的影响较大。而MCJMI则相对于JMI与JMIM稳定性有所提升，MCJMI在选择时结合了两种方法的优点，考虑因素相同的情况下，增加了特征选择的约束条件。MCJMI与SFS-LW在稳定性方面较为一致，但在平稳性一致的情况下，MCJMI的预测精度为0.8060，高于SFS-LW预测精度。表8采用平均精度与稳定性比值来标准化稳定性评判标准，同时考虑精度与稳定性两个方面，通过比值得出MCJMI稳定性最高达到0.92。

6 結语

本文通过比较特征选择方法选择出的特征，在数据集上预测的平均精度、最大预测精度、所需特征数以及稳定性方面比较得出实验结果。MCJMI综合考虑联合互信息与条件互信息，增强了特征选择的约束性，实验结果表明MCJMI能够减少冗余特征的选择。MCJMI也存在不足之处，MCJMI未考虑数据不均衡的情况，未来研究可考虑非平衡数据情况下如何改进。特征选择不仅适用于数据冗余排除，同样适用于因素之间的相关性分析，如物体变形影响因素、城市空气质量影响因素等。

参考文献 （References）

[1] GANDHI S S， PRABHUNE S S. Overview of feature subset selection algorithm for high dimensional data[C]// ICISC 2017： Proceedings of the 2017 IEEE International Conference on Inventive Systems and Control. Piscataway， NJ： IEEE， 2017： 1-6.

[2] FLEURET F. Fast binary feature selection with conditional mutual information [J]. Journal of Machine Learning Research， 2004， 5（3）： 1531-1555.

[3] LIU H， DITZLER G. Speeding up joint mutual information feature selection with an optimization heuristic [C]// Proceedings of the 2017 IEEE Symposium Series on Computational Intelligence. Piscataway， NJ： IEEE， 2018： 1-8.

[4] MIN F， XU J. Semi-greedy heuristics for feature selection with test cost constraints [J]. Granular Computing， 2016， 1（3）： 199-211.

[5] TSAGRIS M， LAGANI V， TSAMARDINOS I. Feature selection for high-dimensional temporal data [J]. BMC Bioinformatics， 2018， 19： 17.

[6] HUANG Z. Based on the information gain text feature selection method [J]. Computer Knowledge and Technology， 2017.

黄志艳.一种基于信息增益的特征选择方法[J].山东农业大学学报（自然科学版）， 2013，44（2）： 252-256.（HUANG Z Y. Based on the information gain text feature selection method [J]. Journal of Shandong Agricultural University （Natural Science）， 2013，44（2）： 252-256.）

[7] 刘海峰，刘守生，宋阿羚.基于词频分布信息的优化IG特征选择方法[J].计算机工程与应用，2017，53（4）：113-117.（LIU H F， LIU S S， SONG A L. Improved method of IG feature selection based on word frequency distribution [J]. Computer Engineering and Applications， 2017， 53（4）： 113-117.）

[8] BATTITI R. Using mutual information for selecting features in supervised neural net learning [J]. IEEE Transactions on Neural Networks， 1994， 5（4）： 537-550.

[9] HOQUE N， BHATTACHARYYA D K， KALITA J K. MIFS-ND： a mutual information-based feature selection method [J]. Expert Systems with Applications， 2014， 41（14）： 6371-6385.

[10] CHO D， LEE B. Optimized automatic sleep stage classification using the Normalized Mutual Information Feature Selection （NMIFS） method [C]// Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Piscataway， NJ： IEEE， 2017： 3094-3097.

[11] PENG H， LONG F， DING C. Feature selection based on mutual information： criteria of max-dependency， max-relevance， and min-redundancy [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2005， 27（8）： 1226-1238.

[12] 董澤民，石强.基于归一化模糊联合互信息最大的特征选择[J].计算机工程与应用，2017，53（22）：105-110.（DONG Z M， SHI Q. Feature selection using normalized fuzzy joint mutual information maximum [J]. Computer Engineering and Applications， 2017， 53（22）： 105-110.）

[13] BENNASAR M， HICKS Y， SETCHI R. Feature selection using joint mutual information maximisation [J]. Expert Systems with Applications， 2015， 42（22）： 8520-8532.

[14] LI J， DONG W， MENG D. Grouped gene selection of cancer via adaptive sparse group lasso based on conditional mutual information [J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics， 2018， 15（6）： 2028-2038.

[15] LIU C， WANG W， ZHAO Q， et al. A new feature selection method based on a validity index of feature subset [J]. Pattern Recognition Letters， 2017， 92： 1-8.

[16] AMARATUNGA D， CABRERA J. High-dimensional data [J]. Journal of the National Science Foundation of Sri Lanka， 2016， 44（1）： 3.

[17] DUA， D. AND KARRA TANISKIDOU， E. （2017）. UCI Machine Learning Repository [http：//archive.ics.uci.edu/ml]. Irvine， CA： University of California， School of Information and Computer Science.

DUA， D. AND KARRA TANISKIDOU， E. UCI Machine Learning Repository [DB/OL]. [2018-07-13]. http：//archive.ics.uci.edu/ml.

[18] ROSS B C. Mutual information between discrete and continuous data sets [J]. PLoS One， 2014， 9（2）： e87357.

[19] CHELVAN P M， PERUMAL K. A study on selection stability measures for various feature selection algorithms [C]// ICCIC 2016： Proceedings of the 2016 IEEE International Conference on Computational Intelligence and Computing Research. Piscataway， NJ： IEEE， 2017： 1-4.