相对投资评价指标及其点估计

文平，宋泓庆

(常州工学院理学院,江苏常州213032)

评价指标在投资研究和实践中起着重要作用。自从Sharpe[1]提出Sharpe比率以来，大量的评价指标被相继提出。1982年，Yitzhaki[2]提出了Gini比率评价指标。Konno等[3]则给出了用MAD比率作为评价指标的思想方法。1994年,Sharpe[4]给出了他的第二个评价指标——信息比率，该比率使我们能够跟踪投资组合和所选择基准之间的表现。2000年，Dowd[5]根据分位数模型提出了一种基于VaR(风险在值)的评价指标。Bernardo等[6]构建了获得-损失比率，旨在通过考虑投资组合的回报率来评估投资组合的吸引力。2001年，Sortino等[7]提出了Sortino比率评价指标。2004年，Biglova等[8]给出了两个评价指标，分别被称为Rachev比率与一般的Rachev比率。此外，文献[9—10]论证了选择评价指标在投资评价中的重要性。

然而上述的评价指标大多数都是绝对评价指标，即评价指标只与投资收益率自身有关而与别的因素无关。

一方面，评价一项投资的好坏不仅要看该项投资的收益率，还要看参照投资的收益率。绝对评价指标主要考虑投资收益率及其波动，比如Sharpe比率、Gini比率、MAD比率等。但随着人们对评价指标认识的不断深入，相对评价指标逐渐受到了理论界与实践工作者的重视。所谓相对评价指标就是与参照投资收益比较时的一个评价指标，近年来提出的评价指标多为相对评价指标，比如Omega指标等。

另一方面，评价指标大多数有其决策理论基础。到目前为止，主要的决策理论有期望效用理论、预期理论和参照依赖偏好理论。上述的评价指标一部分是基于期望效用理论提出的，也有一部分是基于预期理论提出的。Köszegi和Rabin[11-12]在期望效用理论和预期理论基础上提出了参照依赖偏好理论，并被广泛用于经济、管理问题的研究过程中。既然如此，能否根据参照依赖偏好理论构建一个比较好的相对评价指标呢?

1 参照依赖偏好理论

与期望效用理论以及预期理论不同，Köszegi与Rabin认为效用由内在的消费效用函数和获得-损失效用两部分组成。对于无风险收入与参照点， Köszegi与Rabin给出的参照依赖效用函数为：u(x)=m(x)+μ(m(x)-m(r))。其中，m(x)为内在的消费效用函数，μ(m(x)-m(r))为参照依赖的获得-损失效用。 Köszegi与Rabin进一步将参照依赖效用扩展至随机情形。

设X表示随机收益，其分布函数为F(x)，又设Y为随机参照点，其分布函数为G(y)， Köszegi与Rabin给出的参照依赖效用为

(1)

其中，u(x|y)=m(x)+μ(m(x)-m(y))，这里，m(x)为连续可导且单调递增的消费效用函数。

为便于讨论问题， Köszegi和Rabin作了以下假设。第一，消费效用函数可以被假设为线性函数，即m(x)=x；第二，通常可以用一个分段线性函数来描述获得-损失效用函数，即

(2)

这里，λ与η为非负常数。参数λ表示损失厌恶程度。如果λ等于1，决策者属损失中性型；如果λ大于1，决策者属损失厌恶型；如果λ小于1，决策者属损失偏好型。η表示获得-损失效用在决策中的重要性，它越大，获得-损失效用在决策中所起的作用就越大，反之，则是消费效用在决策中所起的作用越大。

为讨论参照依赖效用的具体形式，先介绍一个定义。

定义1[13]设X,Z为两个随机变量，称它们之差的绝对值的数学期望E(|X-Z|)为X到Z的距离，记为S(X,Z)，即

S(X,Z)=E(|X-Z|)

引理1[11-12]假设消费效用函数m(x)为线性函数，获得-损失效用函数μ(x)为形如式(2)分段线性函数。则对于任意X，它相对于参照点Z的参照依赖效用为

(3)

2 相对评价指标及其性质

由引理1结论可知，参照依赖效用主要由两项因素决定。一是客观因素，包括投资收益的数学期望与参照点收益的数学期望的差以及投资收益到参照点的距离。二是主观因素，它包括损失厌恶程度以及获得-损失效用在决策中的重要性。不同的投资者因为其损失厌恶程度以及获得-损失效用在决策中的权重不同，即使选取的参照点相同，面对相同的投资，参照依赖效用也有所不同，所以这里不考虑主观因素对评价指标的影响，只考虑客观因素对评价指标的影响。那么，客观因素如何在评价指标中得到体现呢？从上面引理1可以看出，投资收益的数学期望与参照点收益的数学期望的差越大，参照依赖效用越大，反之亦然。现有的评价指标几乎全部采用比率的形式，在此沿用这种形式。为体现上述两项客观因素对评价指标的影响，可以构建如下的评价指标，用α(X)来表示：

(4)

特别地，如果参照点取无风险收益率rf，则评价指标

(5)

此时的评价指标即为MAD比率，由此可见所构建的评价指标是已有评价指标的推广。下面我们讨论该评价指标的性质。

性质1投资的评价指标-1≤α(X)≤1。

证明该性质非常简单，这里省略。该性质说明评价指标介于-1到1之间，是一个规范性的数学度量。它越接近于1，说明投资的收益率高于参照投资的收益率可能性越大，它等于1说明在各种情况下，投资的收益率均高于参照投资的收益率。它越接近于-1，说明投资的收益率低于参照投资的投资收益率可能性越大，它等于-1说明在各种情况下，投资的收益率均低于参照投资的投资收益率。由此可见，投资的评价指标越接近于1，投资越能跑赢参照投资；投资的评价指标越接近于-1，投资越不能跑赢参照投资。

下面讨论评价指标α(X)的其他性质，要讨论该评价指标的性质，首先来看评价指标所满足的公理。Cherny等[14]在研究评价指标的本质时提出了评价指标所应该满足的特征，他提出评价指标应该满足以下几个特征。

1)半凹

对于评价指标α，定义交易可接受集合Ax={X:α(X)≥x,x∈R+}，半凹要求这个集合是凸集。

2)正齐次性

对于任意w>0有α(wX)=wα(X)。

3)分布不变性

若X与Y具有相同的概率分布，则

α(X)=α(Y)。

4)期望的一致性

假如E(X)<0，则α(X)<0；假如E(X)>0，则α(X)>0。

性质2评价指标α(X)满足半凹性。

S(wX+(1-w)Y,Z)≤wS(X,Z)+

(1-w)S(Y,Z)，

而E(λX+(1-λ)Y)=λE(X)+(1-λ)E(Y)。

所以，

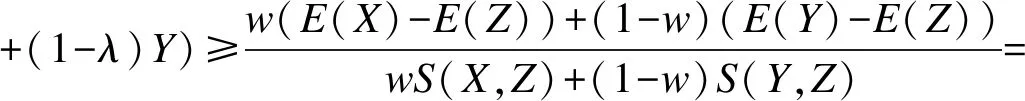
即α(wX+(1-w)Y)≥

从而有α(λX+(1-λ)Y)≥x。

性质3评价指标α(X)满足分布不变性与正齐次性。

证明：若X与Y具有相同的概率分布，则它们的数学期望以及到参照点的距离都相同，故α(X)=α(Y)，评价指标α(X)满足分布不变性。下面证明评价指标α(X)满足正齐次性。

对于任意w>0，由于E(wX)=wE(X)且S(wX,wZ)=wS(X,Z)，故有α(wX)=wα(X)。

性质4评价指标α(X)满足期望一致性。

关于期望的一致性，Cherny主要是针对绝对评价指标而言的。对于相对评价指标，可以将期望一致性修改为：假如E(X)E(Z)，则α(X)>0。显然，评价指标α(X)具有此性质。

3 算例

设X表示某项投资的投资收益，Z为参照投资的投资收益。为了估计X的评价指标，从X中取得简单随机样本X1,X2，…,Xn，从Z中取得简单随机样本Z1,Z2,…,Zn，则X的评价指标的估计量为

(6)

例：本文为了验证所提出的评价指标的准确性，选取了深证股票里面的万科A和顺丰控股两只股票进行计算。根据所查找的数据(数据来源：现价和上一个交易日的收盘价可以从炒股软件获得，如大智慧)计算出2017年日收益率(见表1)。此外，根据中国债券信息网得到的数据，可以计算出2017年的年无风险收益率为2.784%。

表1 统计日收益率的基本资料

根据以上叙述性质与其他指标计算方法，可求得各个指标对应的结果(见表2)。

表2 指标计算结果

根据表2的结果分析，可以看出3个指标的评价结果虽然都指向万科相对于顺丰控股的表现要好一些，但是Sharpe比率在计算单个风险资产受到非系统性的影响几率更大，所以计算出来的效果会大打折扣，MAD比率也指明万科表现更好一些。而本文提出的α(X)此时计算的结果在[-1,1]之间，并且可以明显看出万科的指标值更好一些，即投资万科的收益率高于参照投资的收益率可能性更大。

4 结论

评价指标通常分为相对评价指标、绝对评价指标、基于密度的评价指标以及基于决策的评价指标。目前的研究趋势为：评价指标正在从绝对评价指标向相对评价指标发展，基于密度的评价指标向基于决策的评价指标发展。而基于决策的评价指标因为有决策理论作为基础显得更合理，也就更容易被投资者接受。据此，本文提出了相对评价指标并计算出评价指标的点估计量，并评价了深圳证券交易所两只股票在过去一年内的表现。通过3种指标在评价2只股票中的表现，得出万科股票的投资收益率高于参照指标的收益率可能性更大，证明了相对投资评价指标的优越性。