人工智能背景下投资组合优化问题研究

周新，赵明君

(南京审计大学金融学院，江苏南京211815)

0 引言

近年来，我国经济不断发展，大量资金涌入中国市场。中国的投资市场纷繁复杂，投资方式多样，以股票投资市场为例，股票市场投资组合众多，市场时刻发生变化，风险与收益并存，如何在控制风险情况下实现收益十分重要。

Markowitz[1]阐述了现代投资组合理论的主要思想, 即投资者的效用是关于投资组合的期望收益率和标准差的函数。陈静阳、许若宁[2]指出在投资决策中风险和收益相互影响, 因此应该分散化投资。朱业春、曹崇延[3]在传统的投资组合模型中加入了投资者的主观判断，得出了资产的最优组合权重。朱南、朱传进[4]建立了基于数据挖掘、Kernel回归和现代投资组合优化理论的辅助决策模型，得出了风险最小化的投资组合。

遗传算法来源于进化论、物种选择学说以及群体遗传学说，是模拟自然界生物进化过程与机制求解极值问题的自组织自适应人工智能技术。自Holland[5]提出后，由于其对于难以解决的多目标规划问题有一定的效果，因此遗传算法广泛地应用在各个领域。胡冰等[6]将遗传算法应用于股票短期投资，对投资组合进行了优化。孙雪莲[7]通过使用遗传算法，得出在一定的收益和风险水平下，资产组合的数目是可以降低的结论。齐岳等[8]论证了在大数据背景下，使用遗传算法能够对投资组合进行优化，从而提高收益。

综上所述，结合我国股票市场的特点，在股票数量如此多的今天，穷举计算最优解的方式已经不能有效地给投资者提供投资建议，而突破了表达式限制的遗传算法却能在一定时间内求解出满意解，因此，在此基础上建立的投资组合模型具有投资指导意义。

1 遗传算法设计

1.1 遗传算子设计

本文采用轮盘赌法选择算子，这是一种比例选择方法，即按照适应度来决定个体是否能作为父代将基因遗传到下一代。在使用轮盘赌法选择算子的情况下，高度适应的个体会有更大机会作为父代将基因遗传到下一代，因此在求解最优化问题时计算适应度即可。

本文选用多点交叉算子，共7个交叉点：第1个交叉点为每只股票的位置，第2个交叉点设置为Beta值小于等于1的股票，第3个交叉点设置为Beta值大于1的股票，第4个到第7个交叉点分别设置为日收益率小于等于-0.005的、日收益率大于-0.005到小于等于0的、日收益率大于0到小于等于0.01的、日收益率大于0.01到小于等于0.016的股票。

算子的设置可以使种群的进化方向趋向于最高适应值方向，但同时易使群体单一，失去多样性，算法求解结果陷入局部最优。本文为了防止最优解被变异操作破坏，将变异概率设置为0.01。

1.2 染色体及种群规模

1.2.1 定义染色体

本文所使用染色体的定义和上海A股主板市场的股票数目有关，本文定义基因的方式为股票代码加指标的方式，一个基因代表一只股票，这些基因的组合形成染色体，因而一个染色体就是一种股票组合。本文基因的编码采用二进制编码，即0和1的编码方式。

1.2.2 定义种族规模和最大迭代数目

本文从样本个体空间中随机抽取100条染色体，形成初始种群。定义最终种群的个体数量为20，以21天(7月份的第21个交易日)作为一个预测期，依据7月份的数据来预测8月份的投资组合，最大迭代数目根据算法停滞决定，即适应度不发生明显变化。

1.3 适应值函数和停止准则

本文所设计的适应值函数是针对基因从而扩展到染色体的，即适应值与组成染色体的基因存在函数关系，本文将从基因和染色体两个层面描述适应值函数。其中适应度函数为：

f(Genei)=w1Dret+w2DTrdTurnR+

w3Beta_tmv+w4KDJ

(1)

其中：f(Genei)表示基因适应度函数；w1，w2，w3，w4为权值；Dret表示日收益率；DTrdTurnR表示流通股日换手率，Beta_tmv表示风险因子_流通市值加权，KDJ表示随机指标。

染色体适应值函数为:

(2)

其中：f(Chmi)为染色体函数；n为种群染色体的个数。

由于遗传算法具有收敛性，算法执行后期的适应值变小，种群中的个体之间的差异性降低，此后的计算对满意解向最优解逼近的贡献不大，因此，要定义合适的停止准则，从而高效地求解问题的满意解。本文的停止准则是根据种群的适应度变化程度决定的，当每一代群体的适应度满足一定要求或者适应度变化停滞时，算法停止。

按照设计方案，当算法终止迭代后，将选取适应值最高的一条染色体。该染色体对应的投资组合是所求的全局满意解。

2 实证分析

2.1 数据处理

2.1.1 初始数据

本文所用数据来源于RESSET股票数据库，选取上海证券交易所的所有A股主板股票，得到包含以下指标的数据：股票代码、流通股日换手率、日收益率、21日K值、21日D值、21日J值和风险因子，共1 095只股票，19 612条数据。

2.1.2 确定备选股票集合

利用第一步处理所得数据，剔除公司名称变更、证券代码变更、净资产为负、净利润为负、投资净收益为负的股票，选取剩下正常上市且上市时间大于3个月的股票，确定为初始样本。

经过以上处理后，得到465只股票，再将难以获取到完整数据的股票剔除，最终筛选出413只股票，作为备选股票。所选数据日期为2016年7月份的21个交易日。利用7月份的数据预测优化8月份的投资方案。

2.1.3 数据二进制编码化

本文的数据编码使用二进制编码，在数据二进制化之前，需预先处理现有数据，处理过程如下：

1)由于股票代码数值较大，故将股票代码按从1到413重新编号；

2)由于6个变量的量级不统一，为了便于编码和计算，将其同量级化，同量级化规则：DTrdTurnR×10，Dret×5 000，K21×1，D21×1，J21×1，Beta×100，同量级化后的数据如表1所示(共413条数据，此处仅列示前20条)。

表1 预处理后的备选股票数据表

接下来进行二进制化处理，处理规则为：取数据整数部分进行第一次二进制化，然后测量二进制化后的数字字段长度，取最长字段的位数重新进行二进制计算。经计算测量，最长的二进制字段长度为10位，因此将所有数据转化为长度为10个字符的二进制数据，然后将二进制化后的数据的每个单元作为一个基因片段，按每一行的7个基因片段的顺序生成基因，每一个基因的头部10位为这个基因的顺序编号，共生成413个基因。

2.2 Matlab建模及求解

2.2.1 遗传算法工具箱

遗传算法的实现方式有很多，Matlab软件提供了对应的遗传算法工具箱GADS，遗传算法工具箱中综合了一系列的函数，同时对优化和数值计算工具进行了扩展并提升了性能。工具箱中还提供了一些遗传算法的经典优化问题的范例，以方便快速学习掌握。这个工具箱的函数是用Matlab的M文件格式存储的，可以根据需要修改以实现需要的功能。所有优化算法的函数由Matlab语言编写。

Matlab的遗传算法工具箱的进化规则是逼近适应函数的最小值，因此要对适应函数取负数处理，其他参数按照上文所述设置。

2.2.2 计算结果

算法迭代到第51代终止，计算所得最佳适应度0.283 784，计算结果对应的20只股票及其数据如表2所示。

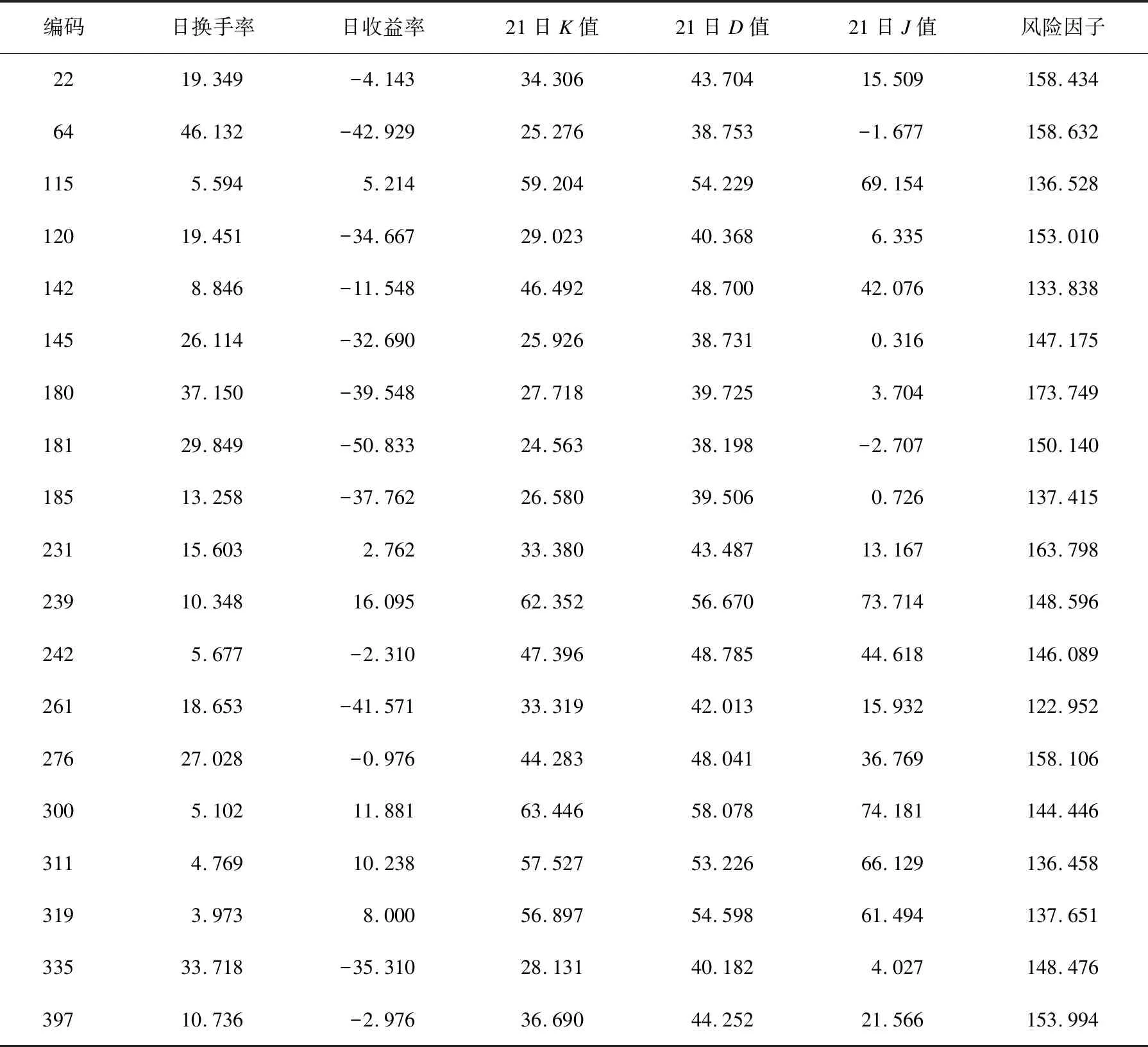
表2 选出股票数据表

8月份同期计算出的组合收益与市场日收益对比如表3所示。

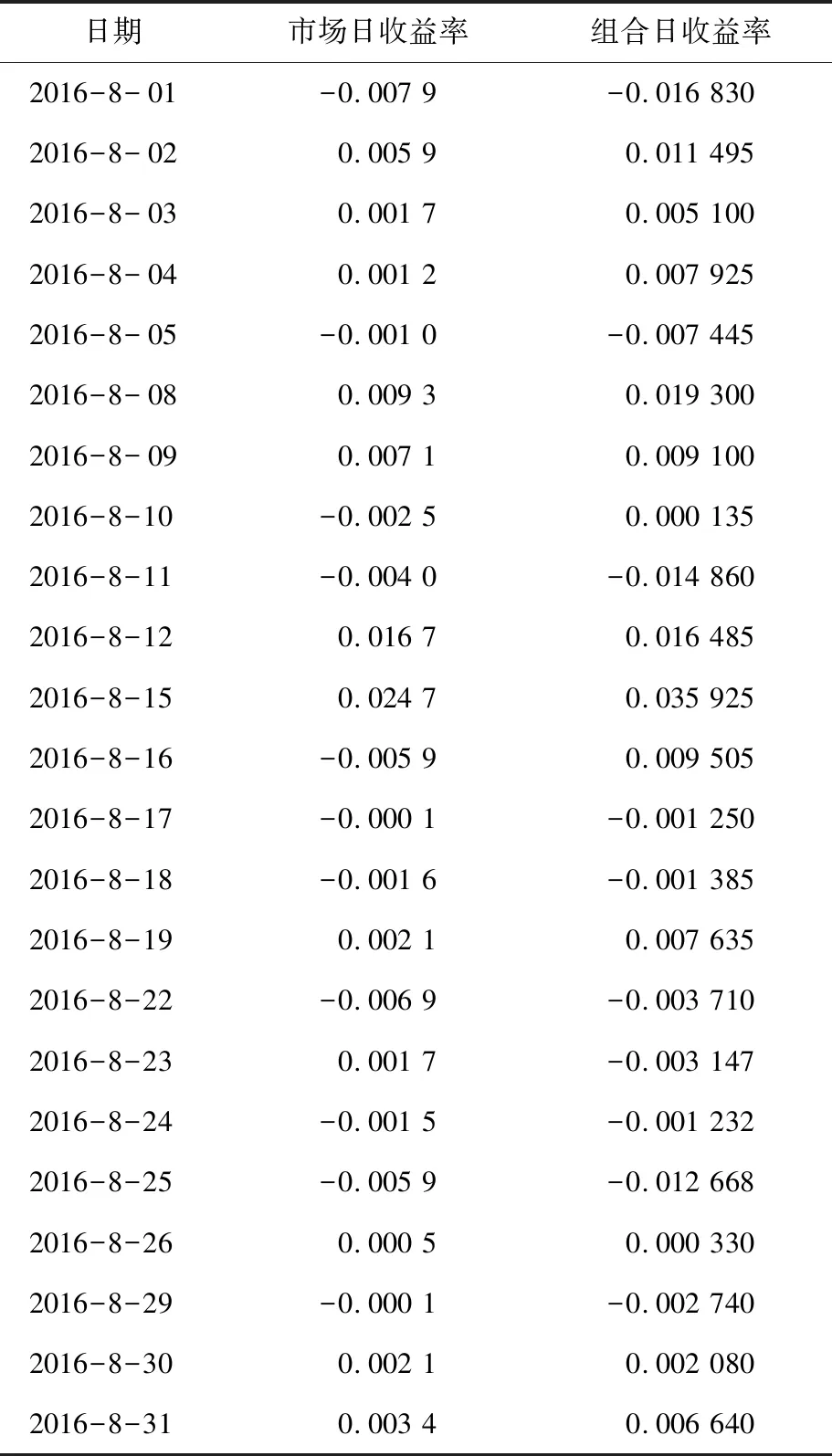
表3 组合收益与市场日收益对比表

表3数据显示：计算出的投资组合的日收益率指标能很好地跟踪市场日收益率指标，2016年8月份A股主板市场的日市场收益率均值为0.001 8，计算出的股票组合的日收益率均值为0.003 018，2016年8月份A股主板市场的日市场收益率加和为0.041 4，计算出的股票组合的日收益率加和为0.069 391，计算出的投资组合的收益率指标要比A股主板市场高出67.61%。

3 结论

伴随着中国经济的高速发展，国民人均收入显著提高，恩格尔系数下降明显，人们的理财习惯从储蓄转变为投资。随着投资市场和各种投资理论的发展，可选择的投资方式和投资领域层出不穷，如何投资才能效益最大化利用资金成为各行各业投资者需要考虑的问题。投资组合理论是一种大众比较接受和认可的理论，通过将资金分散，分散投资风险，从而在可接受风险下获得可观的投资收益。本文选取了股票投资市场作为研究对象，重点研究上海证券交易所的A股主板市场，以投资组合理论作为理论依据、遗传算法作为工具对求解投资组合的优化问题进行了实证研究。本文对遗传算法的各算子、适应值函数进行了详细的设计，并对研究数据作了大量预处理，最终用Matlab工具实现遗传算法并对所研究问题进行了实证。

本文的实证部分得出的结果显示，利用遗传算法求解出的投资组合的日收益率指数能很好地跟踪对应市场日收益率指数，求解出的投资组合的总体收益率要比市场的收益率高出七成，因此，利用遗传算法求解投资组合来对投资组合进行优化是有效的。相较于穷举法搜索全部解的方式，利用遗传算法能在较短的时间内，动用较少的资源，得出足够满意的结果。