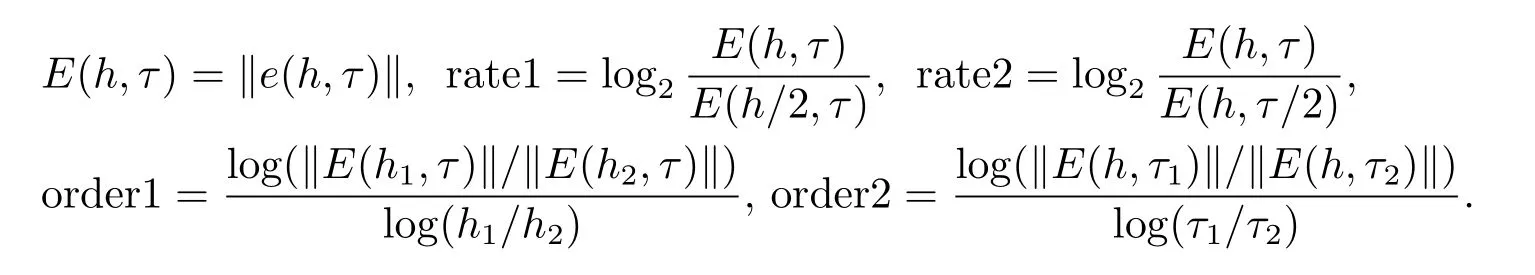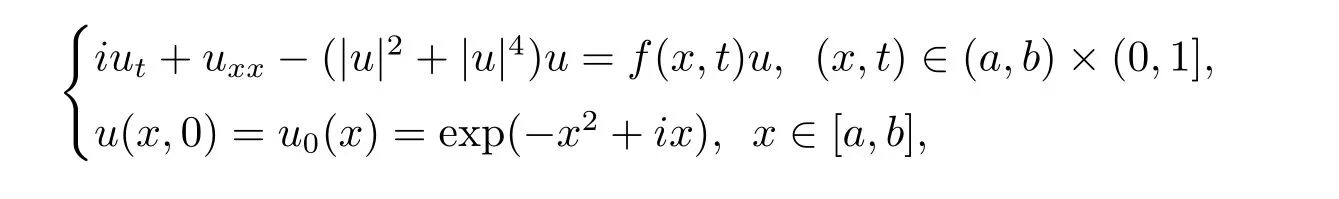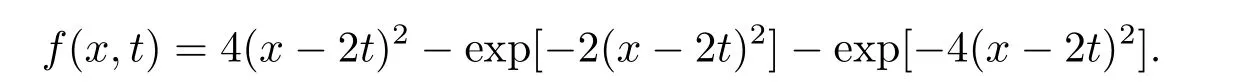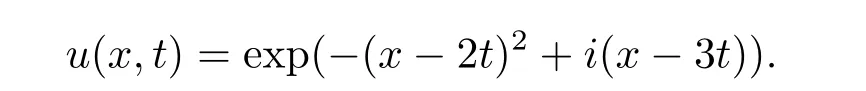五次非线性Schrödinger 方程的一个新型守恒紧致差分格式
2019-07-31王廷春
薛 翔,王廷春
(南京信息工程大学数学与统计学院,江苏南京210044)
1 引言
非线性Schrödinger 方程在量子力学、非线性光学等物理领域有着非常广泛的应用.本文研究如下一类五次非线性Schrödinger 方程的初边值问题[1]
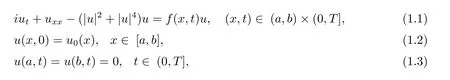
其中f(x,t)为实值函数,u(x,t)为复值函数,u0为已知的复值函数.不难验证,当f(x,t)≡f(x)时,该方程满足两个重要的守恒律,即总质量和总能量守恒[1,2]
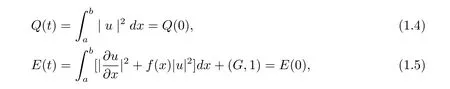
其中
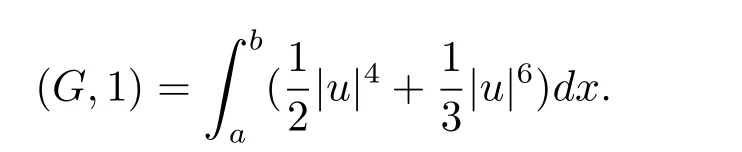
关于非线性Schrödinger 方程的数值研究已有很多结果.Bao 等人[3−5]运用时间分裂拟谱方法对非线性Schrödinger/Gross-Pitaeviskill 方程进行了数值求解,并对某些物理现象进行了数值模拟;Argyris 和Akrivis 等人[6−9]运用有限元法对该方程进行了数值研究;Dehghan 和Mirzaize 运用无网格法对该方程进行了数值求解[10−11].文献[12–14]则运用谱方法和拟谱方法对该方程进行了数值求解和误差分析.因编程简单并能保持原问题的某些守恒性质,有限差分法广泛应用于非线性Schrödinger 方程的数值模拟[15−18].然而关于五次非线性Schrödinger 方程的数值研究尚不多见.张鲁明、常谦顺等人[1−2]对该方程提出两个二阶有限差分格式,证明其保持原问题的两个守恒性质,同时建立了L2范数下的最优误差估计.王询等人[19]用待定系数的方法构建了一类五点有限差分格式,该格式族在选取适当的参数后,其计算精度在空间可达四阶,然而计算中在每一个时间步都需要求解一个五对角代数方程组.为提高精度,文献[20]提出一个紧致有限差分格式,但该格式是非线性的,计算中不可避免的需要迭代,从而降低计算效率.另外,该文作者也没有分析该格式是否在离散意义下保持原问题的两个守恒性质.鉴于以上分析,本文旨在对问题(1.1)–(1.3)构造一个线性化紧致有限差分格式,使得新格式在离散意义下依然保持原问题的两个守恒性质.
2 有限差分格式及其守恒律
对平面区域W=[a,b]×[0,T]进行网格剖分.取正整数J,N,时空方向上的步长分别为网格点分别为
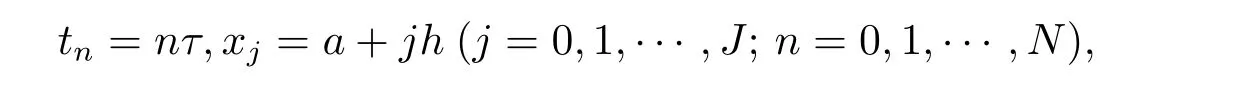
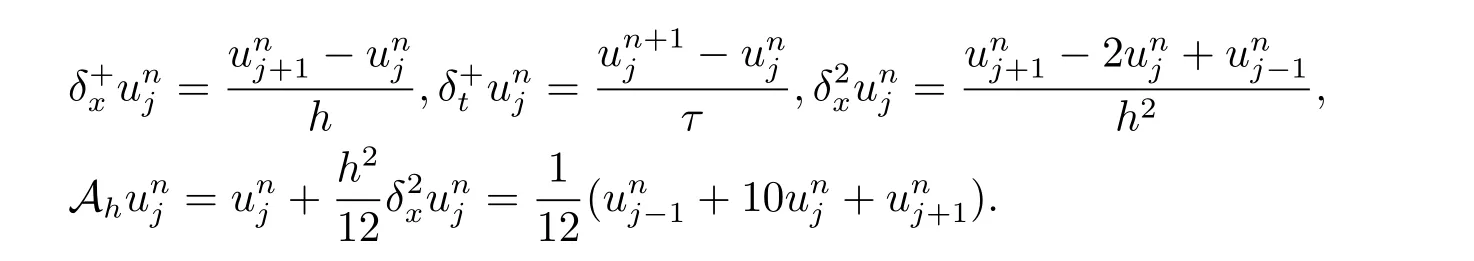
定义Xh={w|w=(ω0,ω1,···,ωJ−1,ωJ),ω0=ωJ=0}为网格函数空间.设u,v 为Xh上的任意两个函数,其内积和范数定义为
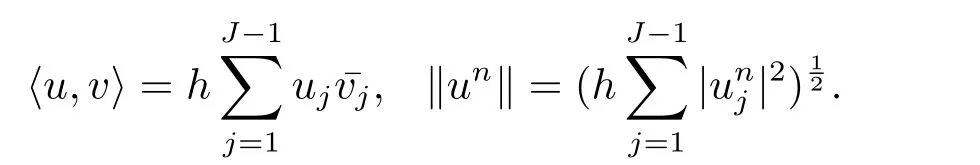
本文需要用到如下引理.
引理1[21]对于任意一个网格函数u ∈Xh,有
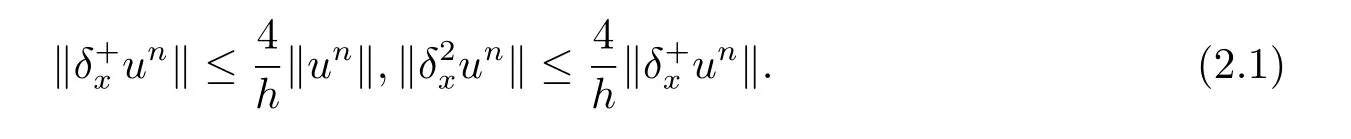
引理2[22]如果网格函数u ∈Xh,则
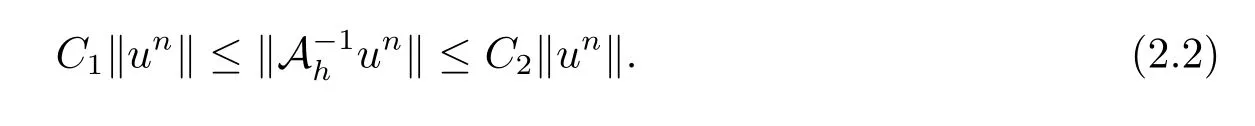
引理3[21]任给网格函数u ∈Xh,有

2.1 有限差分格式
对初边值问题(1.1)–(1.3),本文提出如下四阶紧致差分格式
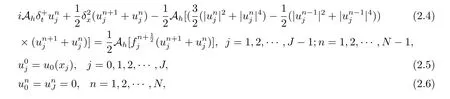
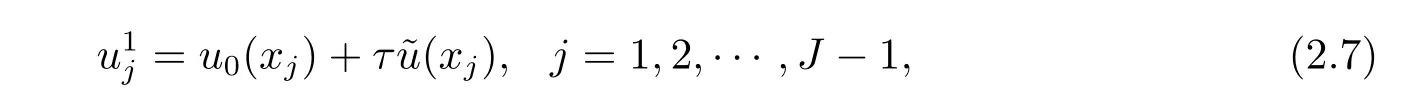
其中
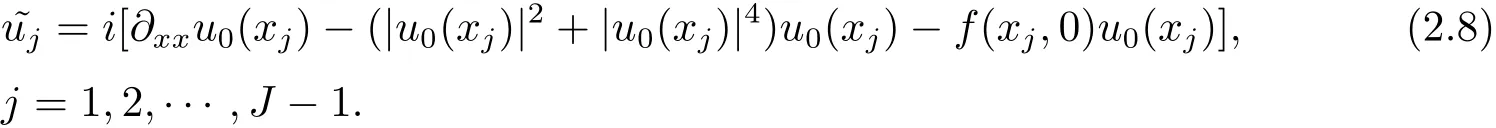
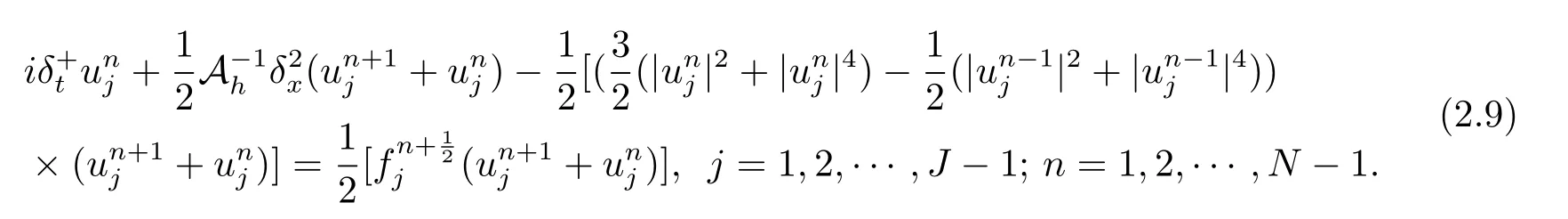
2.2 离散守恒律
为证明离散守恒律,定义
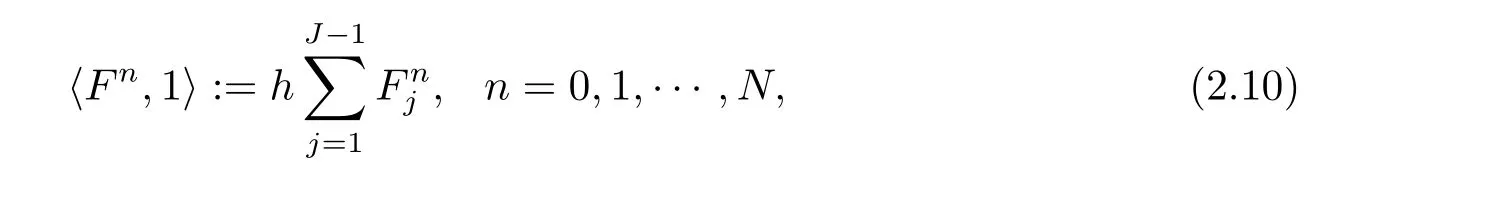
其中
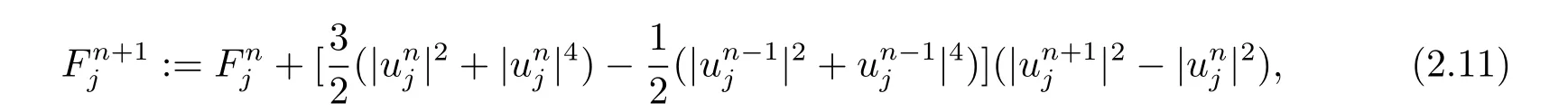
n=1,2,···,N −1,
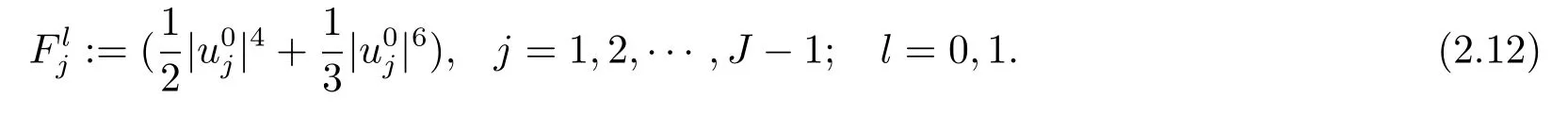
引理4(I)格式(2.4)–(2.6)在离散意义下满足总质量守恒,即
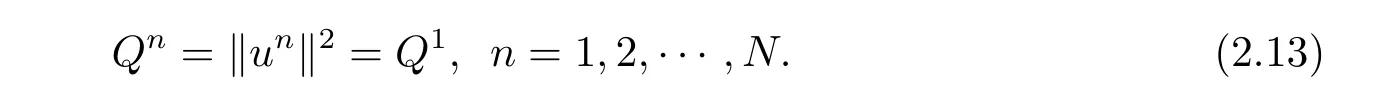
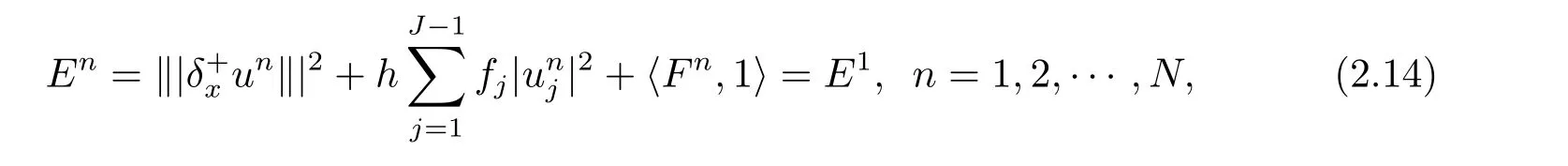
其中
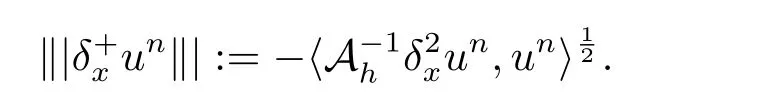
证将(2.9)式与un+1+un做内积,并取虚部得
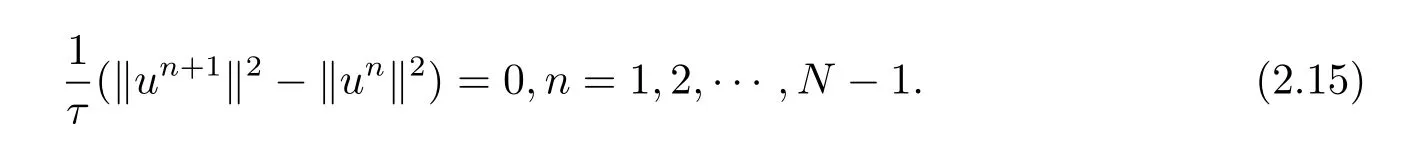
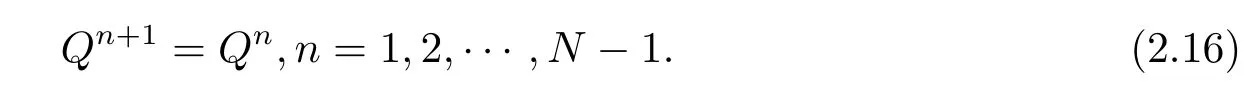
即
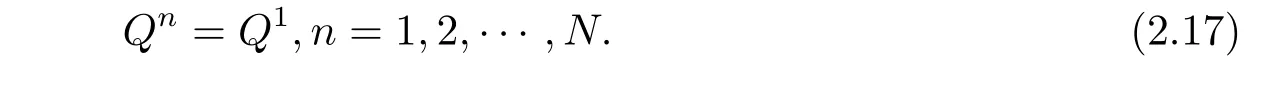
将(2.9)式与un+1−un做内积,并取实部得
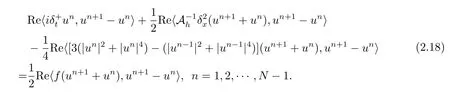
直接计算可得
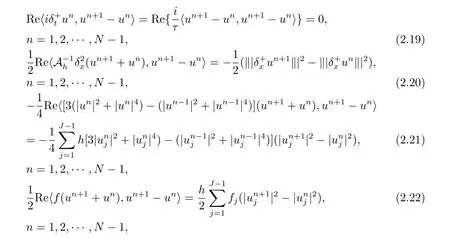
将(2.19)–(2.22)式代入(2.18)式得
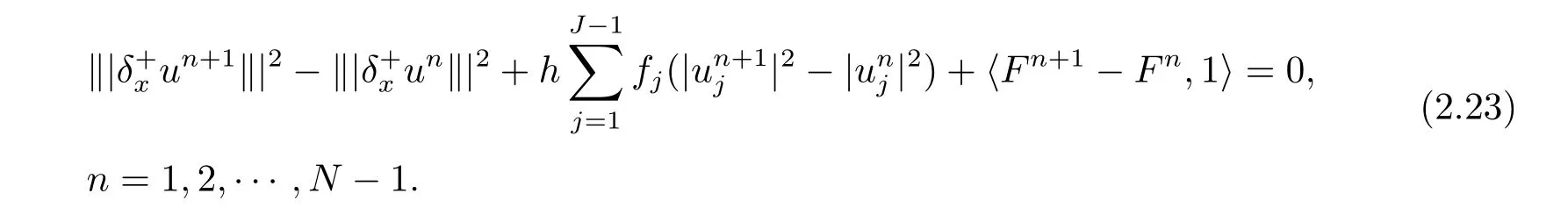
令
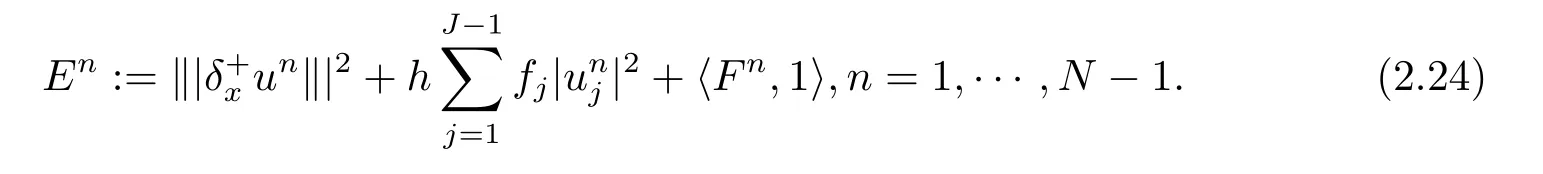
则得
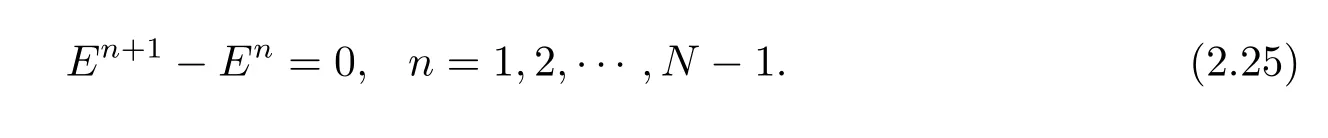
即
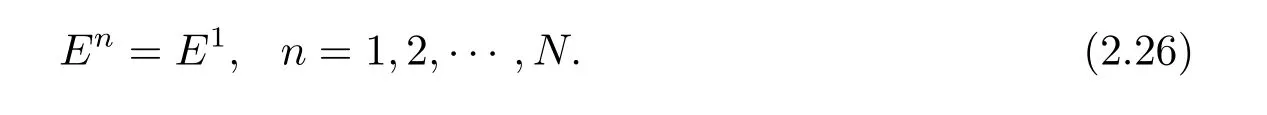
3 误差估计
记格式(2.4)–(2.7)的局部截断误差为
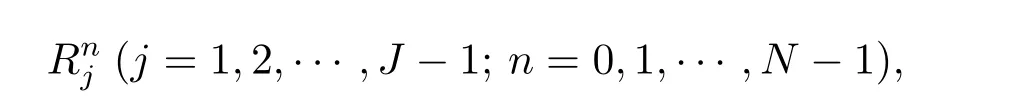
其定义如下

引理5格式(2.4)–(2.7)的局部截断误差满足
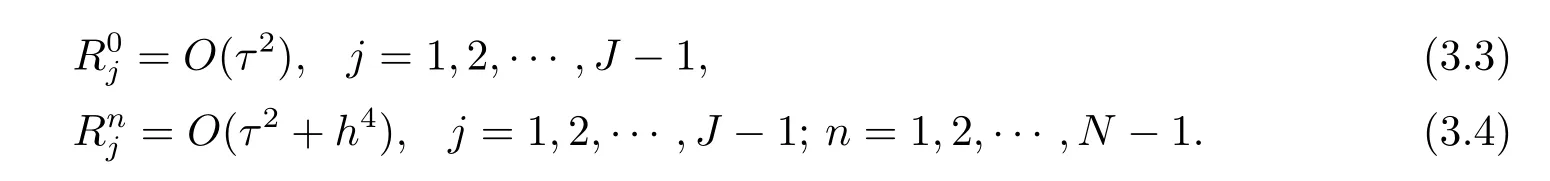
定理1假设u ∈C6,3([a,b]×[0,T]),则差分格式(2.4)–(2.7)的解以·范数收敛到初边值问题(1.1)–(1.3)的解,收敛阶为O(τ2+h4).
证将(3.1)式和(3.2)式分别与(2.7)式和(2.9)式相减可得如下误差方程
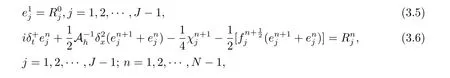
其中
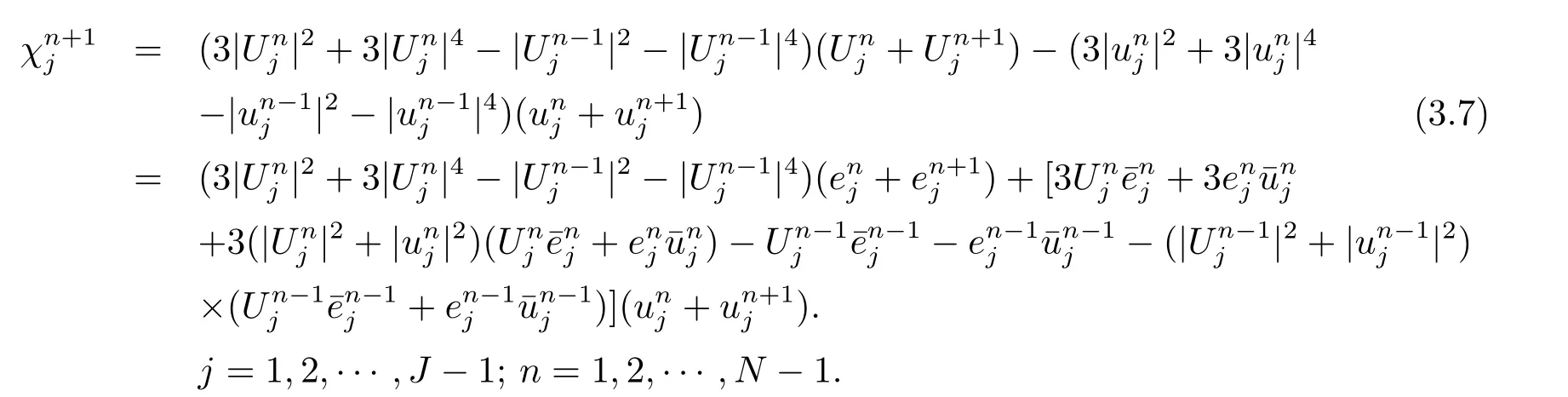
由(3.5)式和引理5 显见

运用Taylor 展开,可得

因此有
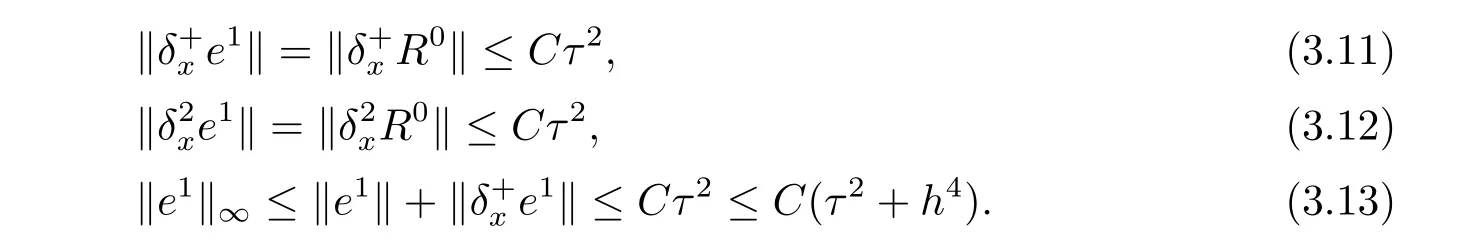
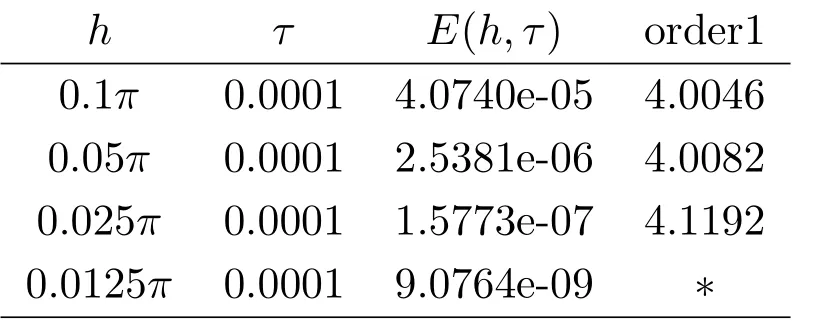
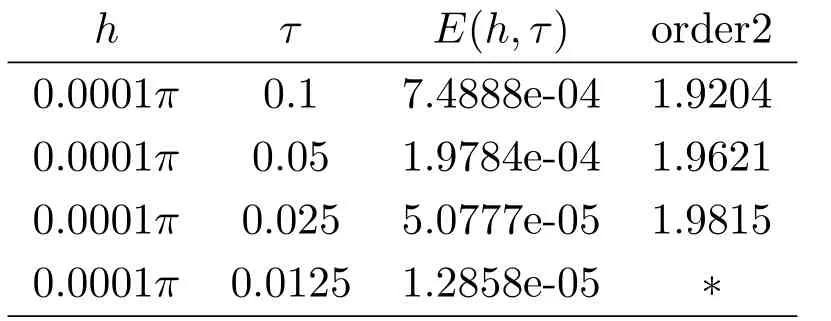
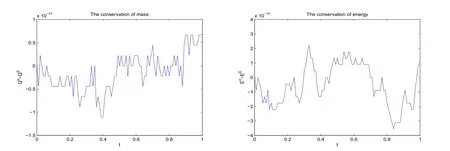
现假设当n ≤k(1 ≤k 进而可得 将(3.6)式与en+en+1做内积,取虚部得 又 由(3.18)–(3.21)式,得 上式对n 求和,有 当τ 足够小时,由Gronwall 不等式得 由(3.6)式可得 运用引理2 有 上式对n 求和得 另外由引理1 可得 由此可见,当τ ≤h 时,有τ2/h2≤1,得 所以无论网格比如何,总有 由(3.24)式和(3.30)式可知假设(3.14)式对n=k+1 时也成立.证毕. 便于验证格式的精度,引入以下记号 算例4.1考虑如下初边值问题 其中 该问题的精确解为 由上式可见当x 趋向于无穷大时,u(x,t)迅速趋于0.故当−a 和b 取得足够大时,u(a,t)和u(b,t)近似为0.因此在数值求解时取空间方向的计算区间为(−15,15),以忽略截断误差的影响. 在验证空间方向(时间方向)收敛阶时,取τ=0.00001(h=0.0001),这样可以忽略时间(空间)方向的误差影响.表1 和表2 分别给出了空间和时间方向的收敛阶.在表3 中,将本文的线性格式与文献[20]中的非线性格式做了计算效率上的比较.图1 展示了精确解和数值解在不同时间层下的波形变化. 表1:空间方向收敛阶 表2:时间方向收敛阶 表3:本文中的线性格式(LCFD)与文[20]中的非线性格式(NCFD)在计算效率上的比较 图1:算例4.1 在τ=0.01,h=0.1 时的精确解(左)和数值解(右) 算例4.2对形如iut+uxx+σ(x,t)u+(β1|u|2+β2|u|4)u=f(x,t),(x,t)∈(0,π)×(0,1].取初始值为u0(x)=sin x,则精确解为u(x,t)=eitsin x. 运用本文中的格式(2.4)–(2.6)对算例4.2 进行求解,有以下结果 表4:空间方向取不同步长时的误差和精度 表5:时间方向取不同步长时的误差和精度 由以上数值实验的结果可看出:差分格式(2.4)–(2.6)在时空方向分别具有2 阶和4 阶精度,而且格式在离散意义下依然能够保持总质量和总能量守恒,这完全符合定理1 和引理4的结论.除此之外,与已有格式相比,本文格式在精度相当的前提下还大幅提高了计算效率. 图2:算例4.2 在不同时间层的总质量(左)和总能量(右) 图3:算例4.2 在离散意义下的总质量守恒(左)和总能量守恒(右)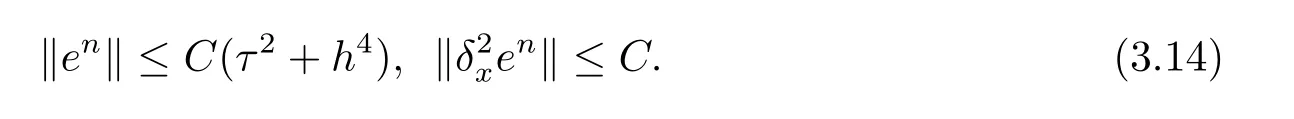
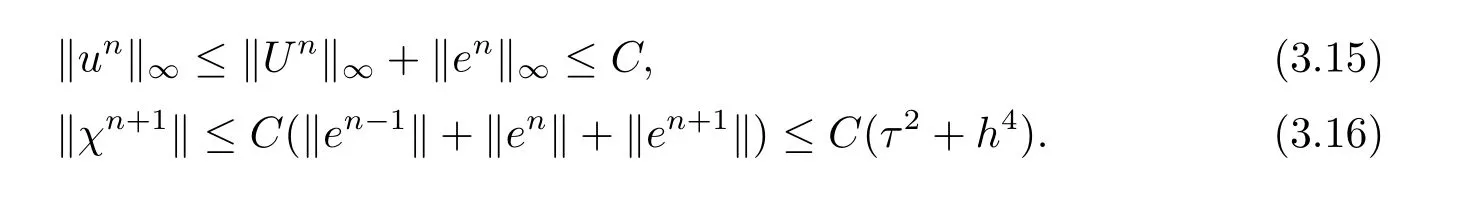
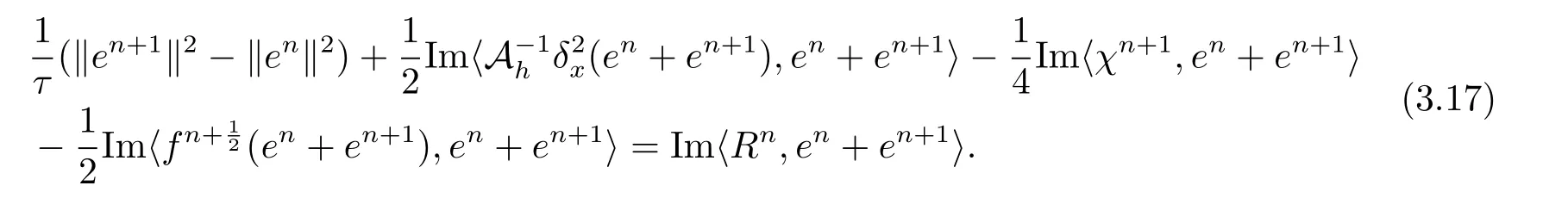
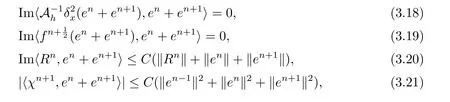
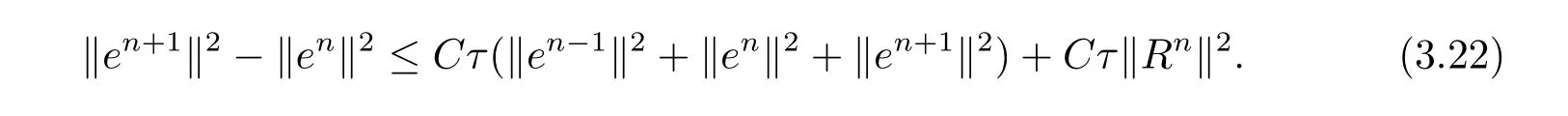
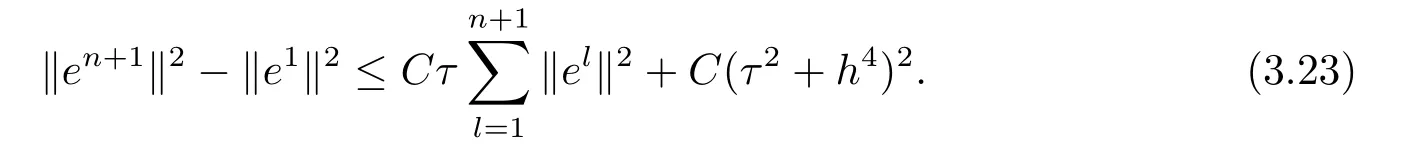

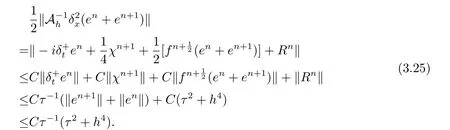
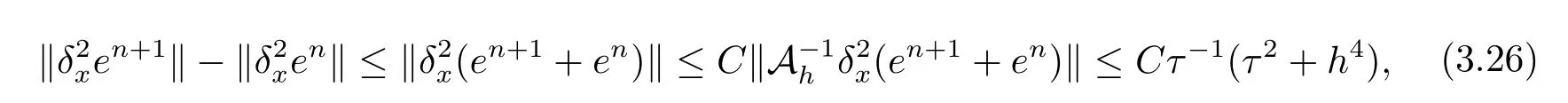
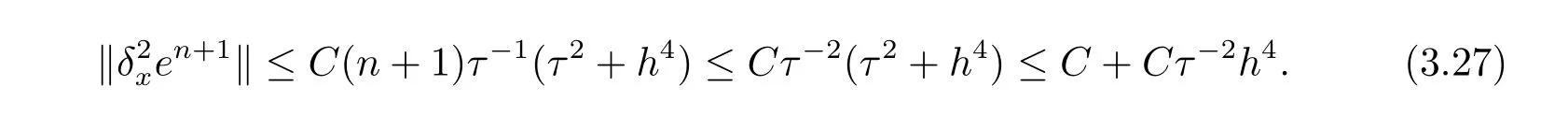



4 数值实验